New Scheme for Validating Remote-Sensing Land Surface Temperature Products with Station Observations
Abstract
:1. Introduction
2. Methodology
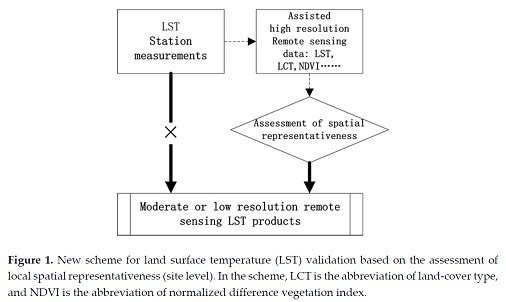
2.1. New Validation Scheme
2.2. Indicators for Assessing Spatial Representativeness
3. Data Instruction and Preparation
3.1. Ground-Based LST Measurements
3.2. Remote-Sensing Data
3.2.1. MODIS Data
3.2.2. High-Spatial-Resolution Images
4. Results and Discussion
4.1. Spatial Representativeness Classification
4.2. Representativeness Grading of the HiWATER Station Observations
4.3. Traditional Validation Results without Spatial Representative Assessment
4.4. MODIS LST Product Validation Considering the Influence of Spatial Representativeness Evaluation
4.5. Other Potential Factors during the LST Validation Process
4.5.1. Dependence of the LST Error on the Sensor VZA
4.5.2. Broadband Sensitivity Issue
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liang, S.L. Quantitative Remote Sensing of Land Surface; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Smith, P.M.; Kalluri, S.N.V.; Prince, S.; Defries, R. The NOAA/NASA pathfinder AVHRR 8-km land data set. Photogramm. Eng. Remote Sens. 1997, 63, 12–27. [Google Scholar]
- El Saleous, N.; Vermote, E.; Justice, C.; Townshend, J.; Tucker, C.; Goward, S. Improvements in the global biospheric record from the Advanced Very High Resolution Radiometer (AVHRR). Int. J. Remote Sens. 2000, 21, 1251–1277. [Google Scholar] [CrossRef]
- Sun, D.; Pinker, R.T. Estimation of land surface temperature from a Geostationary Operational Environmental Satellite (GOES-8). J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Sòria, G.; Romaguera, M.; Guanter, L.; Moreno, J.; Plaza, A.; Martínez, P. Land surface emissivity retrieval from different VNIR and TIR sensors. IEEE Trans. Geosci. Remote Sens. 2008, 46, 316–327. [Google Scholar] [CrossRef]
- Trigo, I.F.; Peres, L.F.; DaCamara, C.C.; Freitas, S.C. Thermal land surface emissivity retrieved from SEVIRI/Meteosat. IEEE Trans. Geosci. Remote Sens. 2008, 46, 307–315. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Coll, C.; Caselles, V.; Galve, J.M.; Valor, E.; Niclos, R.; Sanchez, J.M.; Rivas, R. Ground measurements for the validation of land surface temperatures derived from AATSR and MODIS data. Remote Sens. Environ. 2005, 97, 288–300. [Google Scholar] [CrossRef]
- Coll, C.; Wan, Z.; Galve, J.M. Temperature-based and radiance-based validations of the v5 MODIS land surface temperature product. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z.L. Quality assessment and validation of the MODIS global land surface temperature. Int. J. Remote Sens. 2004, 25, 261–274. [Google Scholar] [CrossRef]
- Wang, K.; Liang, S. Evaluation of ASTER and MODIS land surface temperature and emissivity products using long-term surface longwave radiation observations at SURFRAD sites. Remote Sens. Environ. 2009, 113, 1556–1565. [Google Scholar] [CrossRef]
- Wang, W.; Liang, S.; Meyers, T. Validating MODIS land surface temperature products using long-term nighttime ground measurements. Remote Sens. Environ. 2008, 112, 623–635. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the MODIS land-surface temperature/emissivity products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
- Wang, S.; Li, X.; Ge, Y.; Jin, R.; Ma, M.; Liu, Q.; Wen, J.; Liu, S. Validation of regional-scale remote sensing products in China: From site to network. Remote Sens. 2016, 8, 980. [Google Scholar] [CrossRef]
- Gupta, R.K.; Prasad, T.S.; Krishna Rao, P.V.; Bala Manikavelu, P.M. Problems in upscaling of high resolution remote sensing data to coarse spatial resolution over land surface. Adv. Space Res. 2000, 26, 1111–1121. [Google Scholar] [CrossRef]
- Liu, Y.; Hiyama, T.; Yamaguchi, Y. Scaling of land surface temperature using satellite data: A case examination on ASTER and MODIS products over a heterogeneous terrain area. Remote Sens. Environ. 2006, 105, 115–128. [Google Scholar] [CrossRef]
- Liu, Y.B.; Yamaguchi, Y.; Ke, C.Q. Reducing the discrepancy between aster and MODIS land surface temperature products. Sensors 2007, 7, 3043–3057. [Google Scholar] [CrossRef] [PubMed]
- Hook, S.J.; Vaughan, R.G.; Tonooka, H.; Schladow, S.G. Absolute radiometric in-flight validation of mid infrared and thermal infrared data from ASTER and MODIS on the terra spacecraft using the Lake Tahoe, CA/NV, USA, automated validation site. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1798–1807. [Google Scholar] [CrossRef]
- Yu, W.; Ma, M. Scale mismatch between in situ and remote sensing observations of land surface temperature: Implications for the validation of remote sensing LST products. IEEE Geosci. Remote Sens. Lett. 2015, 12, 497–501. [Google Scholar]
- Xu, B.; Li, J.; Liu, Q.; Huete, A.R.; Yu, Q.; Zeng, Y.; Yin, G.; Zhao, J.; Yang, L. Evaluating spatial representativeness of station observations for remotely sensed leaf area index products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3267–3282. [Google Scholar] [CrossRef]
- Hakuba, M.Z.; Folini, D.; Sanchez-Lorenzo, A.; Wild, M. Spatial representativeness of ground-based solar radiation measurements. J. Geophys. Res. Atmos. 2013, 118, 8585–8597. [Google Scholar] [CrossRef]
- Román, M.O.; Schaaf, C.B.; Woodcock, C.E.; Strahler, A.H.; Yang, X.; Braswell, R.H.; Curtis, P.S.; Davis, K.J.; Dragoni, D.; Goulden, M.L. The MODIS (Collection V005) BRDF/albedo product: Assessment of spatial representativeness over forested landscapes. Remote Sens. Environ. 2009, 113, 2476–2498. [Google Scholar] [CrossRef]
- Janis, M.J.; Robeson, S.M. Determining the spatial representativeness of air-temperature records using variogram-nugget time series. Phys. Geogr. 2004, 25, 513–530. [Google Scholar] [CrossRef]
- Henne, S.; Brunner, D.; Folini, D.; Solberg, S.; Klausen, J.; Buchmann, B. Assessment of parameters describing representativeness of air quality in-situ measurement sites. Atmos. Chem. Phys. 2010, 10, 3561–3581. [Google Scholar] [CrossRef] [Green Version]
- Jia, Z.; Liu, S.; Xu, Z.; Chen, Y.; Zhu, M. Validation of remotely sensed evapotranspiration over the Hai River Basin, China. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Janssen, S.; Dumont, G.; Fierens, F.; Deutsch, F.; Maiheu, B.; Celis, D.; Trimpeneers, E.; Mensink, C. Land use to characterize spatial representativeness of air quality monitoring stations and its relevance for model validation. Atmos. Environ. 2012, 59, 492–500. [Google Scholar] [CrossRef]
- Chan, C.-C.; Hwang, J.-S. Site representativeness of urban air monitoring stations. J. Air Waste Manag. Assoc. 1996, 46, 755–760. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Schaaf, C.B.; Chopping, M.J.; Strahler, A.H.; Wang, J.; Roman, M.O.; Rocha, A.V.; Woodcock, C.E.; Shuai, Y. Evaluation of Moderate-resolution Imaging Spectroradiometer (MODIS) snow albedo product (MCD43A) over tundra. Remote Sens. Environ. 2012, 117, 264–280. [Google Scholar] [CrossRef]
- Chen, B.; Coops, N.C.; Fu, D.; Margolis, H.A.; Amiro, B.D.; Black, T.A.; Arain, M.A.; Barr, A.G.; Bourque, C.P.-A.; Flanagan, L.B. Characterizing spatial representativeness of flux tower eddy-covariance measurements across the Canadian Carbon Program Network using remote sensing and footprint analysis. Remote Sens. Environ. 2012, 124, 742–755. [Google Scholar] [CrossRef]
- Cescatti, A.; Marcolla, B.; Vannan, S.K.S.; Pan, J.Y.; Román, M.O.; Yang, X.; Ciais, P.; Cook, R.B.; Law, B.E.; Matteucci, G. Intercomparison of MODIS albedo retrievals and in situ measurements across the global FLUXNET network. Remote Sens. Environ. 2012, 121, 323–334. [Google Scholar] [CrossRef]
- Wang, Z.; Schaaf, C.B.; Strahler, A.H.; Chopping, M.J.; Román, M.O.; Shuai, Y.; Woodcock, C.E.; Hollinger, D.Y.; Fitzjarrald, D.R. Evaluation of MODIS albedo product (MCD43A) over grassland, agriculture and forest surface types during dormant and snow-covered periods. Remote Sens. Environ. 2014, 140, 60–77. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y.; et al. Heihe watershed allied telemetry experimental research (HiWATER): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Journel, A.G.; Huijbregts, C.J. Mining Geostatistics; Academic Press: London, UK, 1981. [Google Scholar]
- Cressie, N. The origins of kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- Rossi, R.E.; Mulla, D.J.; Journel, A.G.; Franz, E.H. Geostatistical tools for modeling and interpreting ecological spatial dependence. Ecol. Monogr. 1992, 62, 277–314. [Google Scholar] [CrossRef]
- Robertson, G.P. Geostatistics in ecology: Interpolating with known variance. Ecology 1987, 68, 744–748. [Google Scholar] [CrossRef]
- Curran, P.J.; Atkinson, P.M. Geostatistics and remote sensing. Prog. Phys. Geogr. 1998, 22, 61–78. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Tate, N.J. Spatial scale problems and geostatistical solutions: A review. Prof. Geogr. 2000, 52, 607–623. [Google Scholar] [CrossRef]
- Burcsu, T.K.; Robeson, S.M.; Meretsky, V.J. Identifying the distance of vegetative edge effects using Landsat TM data and geostatistical methods. Geocarto Int. 2001, 16, 61–70. [Google Scholar] [CrossRef]
- Li, H.; Reynolds, J. On definition and quantification of heterogeneity. Oikos 1995, 73, 280–284. [Google Scholar] [CrossRef]
- Hu, Y.D.; Gao, J.M.; Wang, J.M.; Ji, G.L.; Shen, Z.B.; Cheng, L.S.; Chen, J.Y.; Li, S.Q. Some achievements in scientific research during HEIFE. Plateau Meteorol. 1994, 13, 225–236. [Google Scholar]
- Li, X.; Li, X.; Li, Z.; Ma, M.; Wang, J.; Xiao, Q.; Liu, Q.; Che, T.; Chen, E.; Yan, G.; et al. Watershed allied telemetry experimental research. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Heihe Watershed Allied Telemetry Experimental Research (HiWATER) Home. Available online: http://card.westgis.ac.cn/hiwater (accessed on 17 March 2017).
- Wang, K.; Wan, Z.; Wang, P.; Sparrow, M.; Liu, J.; Zhou, X.; Haginoya, S. Estimation of surface long wave radiation and broadband emissivity using Moderate Resolution Imaging Spectroradiometer (MODIS) land surface temperature/emissivity products. J. Geophys. Res. Atmos. 2005, 110, D11109. [Google Scholar] [CrossRef]
- Salomonson, V.V.; Barnes, W.; Maymon, P.W.; Montgomery, H.E.; Ostrow, H. Modis: Advanced facility instrument for studies of the earth as a system. IEEE Trans. Geosci. Remote Sens. 1989, 27, 145–153. [Google Scholar] [CrossRef]
- Wan, Z.M.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Wan, Z.M.; Li, Z.L. A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 980–996. [Google Scholar]
- Seemann, S.W.; Li, J.; Gumley, L.E.; Strabala, K.I.; Menzel, W.P. Operational retrieval of atmospheric temperature, moisture, and ozone from MODIS infrared radiances. J. Appl. Meteorol. 2003, 42, 1072–1091. [Google Scholar] [CrossRef]
- HiWATER: Land Cover Map of Heihe River Basin. Available online: http://card.westgis.ac.cn/hiwater/rsproduct (accessed on 21 March 2017).
- Zhong, B.; Ma, P.; Nie, A.; Yang, A.; Yao, Y.; Lü, W.; Zhang, H.; Liu, Q. Land cover mapping using time series HJ-1/CCD data. Sci. China Earth Sci. 2014, 57, 1790–1799. [Google Scholar] [CrossRef]
- Zhong, B.; Yang, A.; Nie, A.; Yao, Y.; Zhang, H.; Wu, S.; Liu, Q. Finer resolution land-cover mapping using multiple classifiers and multisource remotely sensed data in the Heihe River Basin. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4973–4992. [Google Scholar] [CrossRef]
- Zhong, B.; Zhang, Y.; Du, T.; Yang, A.; Lv, W.; Liu, Q. Cross-calibration of HJ-1/CCD over a desert site using Landsat ETM + Imagery and ASTER GDEM product. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7247–7263. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.; Loveland, T.; Woodcock, C.; Allen, R.; Anderson, M.; Helder, D.; Irons, J.; Johnson, D.; Kennedy, R. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Du, C.; Ren, H.; Qin, Q.; Meng, J.; Zhao, S. A practical split-window algorithm for estimating land surface temperature from Landsat 8 data. Remote Sens. 2015, 7, 647–665. [Google Scholar] [CrossRef]
- USGS Home. Available online: https://glovis.usgs.gov/ (accessed on 4 February 2017).
- MODIS Land Cover Product Algorithm Theoretical Basis Document (ATBD) Version 5.0. Available online: http://modis.gsfc.nasa.gov/data/atbd/land_atbd.php (accessed on 2 May 2016).
- Ermida, S.L.; Trigo, I.F.; DaCamara, C.C.; Göttsche, F.M.; Olesen, F.S.; Hulley, G. Validation of remotely sensed surface temperature over an oak woodland landscape—The problem of viewing and illumination geometries. Remote Sens. Environ. 2014, 148, 16–27. [Google Scholar] [CrossRef]
- Xu, Z.W.; Liu, S.M.; Li, X.; Shi, S.J.; Wang, J.M.; Zhu, Z.L.; Xu, T.R.; Wang, W.Z.; Ma, M.G. Intercomparison of surface energy flux measurement systems used during the HiWATER-MUSOEXE. J. Geophys. Res. 2013, 118, 13140–13157. [Google Scholar] [CrossRef]
- Yu, W.; Ma, M.; Wang, X.; Geng, L.; Tan, J.; Shi, J. Evaluation of MODIS LST products using longwave radiation ground measurements in the northern arid region of China. Remote Sens. 2014, 6, 11494–11517. [Google Scholar] [CrossRef]












| Station Name | Longitude/°E | Latitude/°N | Altitude/m | Height/m | Footprint 1/m | Landscapes |
|---|---|---|---|---|---|---|
| A’rou superstation (ARC) | 100.46 | 38.05 | 3033 | 5 | 37.32 | Alpine meadow |
| A’rou sunny slope station (ARS) | 100.52 | 38.09 | 3559 | 6 | 44.78 | Alpine grassland |
| A’rou shade station (ARY) | 100.42 | 37.99 | 3538 | 6 | 44.78 | Alpine grassland |
| Dashalong station (DSL) | 98.95 | 38.83 | 3775 | 6 | 44.78 | Swamp meadow |
| Jinyangling station (JYL) | 101.11 | 37.85 | 3700 | 6 | 44.78 | Alpine meadow |
| Huangzangsi station (HZS) | 100.19 | 38.23 | 2660 | 6 | 44.78 | Cropland (wheat) |
| Huangcaogou station (HCG) | 100.73 | 38.00 | 3186 | 6 | 44.78 | Alpine grassland |
| E’bo station (EBZ) | 100.94 | 37.96 | 3407 | 6 | 44.78 | Alpine grassland |
| Daman superstation (DMZ) | 100.37 | 38.86 | 1519 | 12 | 89.57 | Cropland (maize) |
| Gobi station (GBZ) | 100.30 | 38.89 | 1571 | 6 | 44.78 | Gobi Desert |
| Huazhaizi desert station (HZZ) | 100.32 | 38.77 | 1726 | 2.5 | 18.66 | Desert steppe |
| Wetland station (SDZ) | 100.45 | 38.97 | 1460 | 6 | 44.78 | Wetland |
| Shenshawo desert station (SSW) | 100.49 | 38.79 | 1582 | 6 | 44.78 | Desert |
| Populus forest station (HYZ) | 101.12 | 41.99 | 927 | 24 | 179.14 | Populus forest |
| Cropland station (NTZ) | 101.13 | 42.01 | 919 | 6 | 44.78 | Cropland |
| Barren-land station (LTZ) | 101.13 | 41.99 | 931 | 6 | 44.78 | Bare soil |
| Sidaoqiao station (SDQ) | 101.12 | 41.99 | 935 | 10 | 74.64 | Euphrates poplar olive and Tamarix mixed forest |
| Mixed forest station (HJL) | 101.13 | 41.99 | 929 | 24 | 179.14 | Euphrates poplar olive and Tamarix mixed forest |
| Level | DLCT > 60% | RB < 0.5% | ASS > 1 km | Description |
|---|---|---|---|---|
| 1 | √ | √ | √ | Best representativeness level with strict point-to-pixel LST and LCT value consistency, and a homogeneous LST distribution |
| 2 | √ | √ | × | High representativeness level with high point-to-pixel LST and LCT value consistency but an incomplete homogeneous LST distribution |
| 3 | √ | × | √ | Moderate representativeness level with high LCT consistency and a relatively homogeneous LST distribution but low point-to-area LST consistency |
| 4 | √ | × | × | Low representativeness level with low point-to-area LST consistency and a heterogeneous LST distribution |
| 5 | × | - | - | Minimal representativeness level with various LCTs in pixels and mismatch land-cover observations |
| Station | MOD a | MYD b | ||||||
|---|---|---|---|---|---|---|---|---|
| Day | Night | Day | Night | |||||
| Bias | RMSE | Bias | RMSE | Bias | RMSE | Bias | RMSE | |
| ARC | −0.55 | 2.16 | 0.98 | 2.15 | −0.52 | 1.92 | 0.67 | 1.94 |
| ARY | −0.79 | 5.50 | −0.51 | 2.25 | −0.96 | 4.48 | −0.28 | 2.56 |
| ARS | 0.31 | 2.56 | 0.01 | 2.64 | 0.56 | 2.54 | −0.39 | 2.57 |
| DSL | 1.07 | 1.74 | 1.25 | 1.22 | 0.89 | 1.87 | 1.27 | 2.16 |
| JYL | −2.79 | 3.14 | 0.96 | 1.41 | −2.94 | 3.09 | 0.47 | 2.26 |
| HZS | 0.10 | 3.49 | 1.65 | 1.19 | −0.13 | 3.73 | 0.96 | 1.94 |
| HCG | −1.31 | 2.36 | 0.62 | 1.96 | −1.68 | 2.92 | −0.25 | 2.33 |
| EBZ | −0.78 | 2.07 | 0.77 | 1.61 | −0.97 | 2.39 | 0.23 | 2.56 |
| DMZ | −0.88 | 2.81 | 1.23 | 1.45 | −0.96 | 2.77 | 0.21 | 2.21 |
| GBZ | 0.17 | 2.25 | −0.01 | 1.52 | 1.08 | 1.75 | 0.66 | 2.99 |
| HZZ | 0.74 | 1.86 | 0.93 | 1.28 | 0.25 | 2.46 | 0.69 | 2.08 |
| SDZ | −4.12 | 2.93 | 1.90 | 2.74 | −3.44 | 2.71 | 1.26 | 3.78 |
| SSW | 1.34 | 4.18 | 2.49 | 1.60 | 1.57 | 2.95 | 1.55 | 2.51 |
| SDQ | −1.84 | 3.18 | 1.95 | 1.21 | −1.65 | 2.35 | 1.50 | 3.80 |
| HJL | −4.23 | 2.70 | 3.56 | 1.90 | −4.55 | 2.81 | 3.48 | 3.82 |
| HYZ | −0.72 | 5.18 | 3.86 | 2.03 | −0.71 | 5.94 | 2.75 | 3.14 |
| NTZ | −4.72 | 4.08 | 1.43 | 1.47 | −0.17 | 5.44 | 1.15 | 2.91 |
| LTZ | 6.46 | 4.21 | 2.45 | 1.15 | 6.24 | 3.68 | 1.77 | 3.02 |
| Level | MOD a | MYD b | ||||||
|---|---|---|---|---|---|---|---|---|
| Day | Night | Day | Night | |||||
| Bias | RMSE | Bias | RMSE | Bias | RMSE | Bias | RMSE | |
| Level 1 | −0.19 | 1.75 | 0.8 | 1.58 | 0.30 | 1.79 | 0.43 | 1.84 |
| Level 2 | −1.13 | 4.58 | 1.24 | 2.53 | −1.48 | 3.24 | 0.32 | 2.60 |
| Level 3 | 1.45 | 4.93 | 1.44 | 2.23 | 0.47 | 3.67 | 0.77 | 2.67 |
| Level 4 | −2.94 | 5.93 | 2.51 | 3.89 | −2.25 | 4.56 | 1.33 | 4.15 |
| Level 5 | 2.03 | 6.27 | 3.60 | 4.52 | −0.36 | 5.88 | 2.28 | 4.29 |
| All | 0.59 | 4.93 | 2.39 | 3.55 | −0.27 | 4.58 | 1.28 | 3.32 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, W.; Ma, M.; Li, Z.; Tan, J.; Wu, A. New Scheme for Validating Remote-Sensing Land Surface Temperature Products with Station Observations. Remote Sens. 2017, 9, 1210. https://doi.org/10.3390/rs9121210
Yu W, Ma M, Li Z, Tan J, Wu A. New Scheme for Validating Remote-Sensing Land Surface Temperature Products with Station Observations. Remote Sensing. 2017; 9(12):1210. https://doi.org/10.3390/rs9121210
Chicago/Turabian StyleYu, Wenping, Mingguo Ma, Zhaoliang Li, Junlei Tan, and Adan Wu. 2017. "New Scheme for Validating Remote-Sensing Land Surface Temperature Products with Station Observations" Remote Sensing 9, no. 12: 1210. https://doi.org/10.3390/rs9121210
APA StyleYu, W., Ma, M., Li, Z., Tan, J., & Wu, A. (2017). New Scheme for Validating Remote-Sensing Land Surface Temperature Products with Station Observations. Remote Sensing, 9(12), 1210. https://doi.org/10.3390/rs9121210