Moisture Content Measurement of Broadleaf Litters Using Near-Infrared Spectroscopy Technique
Abstract
:1. Introduction
2. Materials and Methods
2.1. Litter Moisture Measurement
2.2. NIR Spectra Measurement
2.3. Multivariate Model Development
2.4. Estimation of Prediction Uncertainty
2.5. Optimal Wavelength Selection
2.5.1. Peak of Beta Coefficient
2.5.2. Variable Importance in Projection
2.5.3. Bootstrap of Beta Coefficients
2.5.4. Interval PLS
3. Results
3.1. Reflectance Spectra of Litters
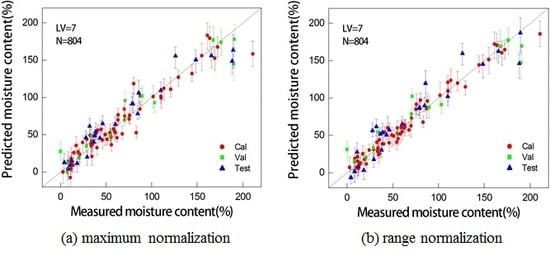
3.2. PLSR Model for Different Preprocessing Methods
3.3. PLSR Models for Optimal Wavelength Selection Methods
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ataka, M.; Kominami, Y.; Miyama, T.; Yoshimura, K.; Jomura, M.; Tani, M. Using capacitance sensors for the continuous measurement of the water content in the litter layer of forest soil. Appl. Environ. Soil Sci. 2014. [Google Scholar] [CrossRef]
- Stocks, B.J. Moisture in the Forest Floor—Its Distribution and Movement; Department of Fisheries and Forestry, Canadian Forestry Service: Ottawa, ON, Canada, 1970; p. 20.
- Xiao, Q.; McPherson, E.G. Surface water storage of twenty tree species in Davis, California. J. Environ. Qual. 2016, 45, 188–198. [Google Scholar] [CrossRef]
- Borken, W.; Matzner, E. Reappraisal of drying and wetting effects on C and N mineralization and fluxes in soils. Glob. Chang. Biol. 2009, 15, 808–824. [Google Scholar] [CrossRef]
- Johnson, E.A.; Miyanishi, K. Forest Fires: Behavior and Ecological Effects; Academic Press: Washington, DC, USA, 2001; p. 594. [Google Scholar]
- Schunk, C.; Ruth, B.; Leuchner, M.; Wastl, C.; Menzel, A. Comparison of different methods for the in situ measurement of forest litter moisture content. Nat. Hazard Earth Syst. Sci. 2016, 16, 403–415. [Google Scholar] [CrossRef]
- Wotton, B.M.; Stocks, B.; Martell, D.L. An index for tracking sheltered forest floor moisture with the Canadian Forest Fire Weather Index System. Int. J. Wildland Fire 2005, 14, 169–182. [Google Scholar] [CrossRef]
- Gillespie, T.J.; Kidd, G. Sensing duration of leaf moisture retention using electrical impedance grids. Can. J. Plant Sci. 1978, 58, 179–187. [Google Scholar] [CrossRef]
- Hanson, P.J.; O’Neill, E.G.; Chambers, M.L.S.; Riggs, J.S.; Joslin, J.D.; Wolfe, M.H. Soil respiration and litter decomposition. In North America Temperature Deciduous Forests Response to Changing Precipitation Regimes; Hanson, P.J., Wullschleger, S.D., Eds.; Springer: New York, NY, USA, 2003; pp. 163–189. [Google Scholar]
- Borner, T.; Johnson, M.G.; Ryglewlcz, P.T.; Tingey, D.T.; Jarrell, G.D. A two-probe method for measuring water content of thin forest floor litter layers using time domain reflectometry. Soil Technol. 1996, 9, 199–207. [Google Scholar] [CrossRef]
- Pumpanen, J.; Ilvesniemi, H. Calibration of time domain reflectometry for forest soil humus layers. Boreal Environ. Res. 2005, 10, 589–595. [Google Scholar]
- Robichaud, P.R.; Bilskie, J. A new tool for fire managers-an electronic duff moisture meter. Fire Manag. Today 2004, 64, 15–18. [Google Scholar]
- Hong, S.-J.; Rho, S.-J.; Lee, A.-Y.; Park, H.; Cui, J.; Park, J.; Hong, S.-J.; Kim, Y.-R.; Kim, G. Rancidity estimation of perilla seed oil by using near-infrared spectroscopy and multivariate analysis techniques. J. Spectrosc. 2017, 2017, 1–10. [Google Scholar] [CrossRef]
- Kim, W.-K.; Hong, S.-J.; Cui, J.; Kim, H.-J.; Park, J.; Yang, S.-H.; Kim, G. Application of NIR spectroscopy and artificial neural network techniques for real-time discrimination of soil categories. J. Korean Soc. Nondestruct. Test. 2017, 6, 148–157. [Google Scholar] [CrossRef]
- Lohumi, S.; Kandpal, L.M.; Seo, Y.W.; Cho, B.K. Net analyte signal-based quantitative determination of fusel oil in Korean alcoholic beverage using FT-NIR spectroscopy. J. Biosyst. Eng. 2016, 41, 208–220. [Google Scholar] [CrossRef]
- Liu, Y.; Kim, H.-J. Fourier transform infrared spectroscopy (FT-IR) and simple algorithm analysis for rapid and non-destructive assessment of developmental cotton fibers. Sensors 2017, 17, 1469. [Google Scholar] [CrossRef] [PubMed]
- Lefcourt, A.M.; Kistler, R.; Gadsden, S.A.; Kim, M.S. Automated cart with VIS/NIR hyperspectral reflectance and fluorescence imaging capabilities. Appl. Sci. 2017, 7, 3. [Google Scholar] [CrossRef]
- Kim, G.S.; Kim, D.-Y.; Kim, G.H.; Cho, B.-K. Applications of discrete wavelet analysis for predicting internal quality of cherry tomatoes using VIS/NIR spectroscopy. J. Biosyst. Eng. 2013, 38, 48–51. [Google Scholar] [CrossRef]
- ASTM International. American Society for Testing and Materials, E1866-97: Standard Guide for Establishing Spectrophotometer Performance Tests; E1655: Standard Practices for Infrared, Multivariate, Quantitative Analysis; Official ASTM Publications: Philadelphia, PA, USA, 2000. [Google Scholar]
- Choe, E.; van der Meer, F.; van Ruitenbeek, F.; van der Werff, H.; de Smeth, B.; Kim, K.W. Mapping of heavy metal pollution in stream sediments using combined geochemistry, field spectroscopy, and hyperspectral remote sensing: A case study of the Rodalquilar mining area, SE Spain. Remote Sens. Environ. 2008, 112, 3222–3233. [Google Scholar] [CrossRef]
- Choi, C.H.; Lee, K.J.; Park, B.S. Prediction of soluble solid and firmness in apple by visible/near-infrared spectroscopy. J. Korean Soc. Agric. Mach. 1997, 22, 256–265. (In Korean) [Google Scholar]
- Lu, R.F.; Guyer, D.E.; Beaudry, R.M. Determination of firmness and sugar content of apples using near-infrared diffuse reflectance. J. Texture Stud. 2000, 31, 615–630. [Google Scholar] [CrossRef]
- Dalal, R.C.; Henry, R.J. Simultaneous determination of moisture, organic carbon, and total nitrogen by near infrared reflectance spectrophotometry. Soil Sci. Soc. Am. J. 1986, 50, 120–123. [Google Scholar] [CrossRef]
- Ludwig, B.; Khanna, P.K.; Bauhus, J.; Hopmans, P. Near infrared spectroscopy of forest soils to determine chemical and biological properties related to soil sustainability. For. Ecol. Manag. 2002, 171, 121–132. [Google Scholar] [CrossRef]
- Martin, P.D.; Malley, D.F.; Manning, G.; Fuller, L. Determination of soil organic carbon and nitrogen at the field level using near infrared spectroscopy. Can. J. Soil Sci. 2002, 82, 413–422. [Google Scholar] [CrossRef]
- Card, D.H.; Peterson, D.J.; Matson, P.A.; Aber, J.D. Prediction of leaf chemistry by the use of visible and near-infrared reflectance spectroscopy. Remote Sens. Environ. 1988, 26, 123–147. [Google Scholar] [CrossRef]
- Wessman, C.A.; Aber, J.D.; Peterson, D.L.; Melillo, J.M. Foliar analysis using near-infrared reflectance spectroscopy. Can. J. For. Res. 1988, 18, 6–11. [Google Scholar] [CrossRef]
- Martin, M.E.; Aber, J.D. Analysis of forest foliage. III: Determining nitrogen, lignin and cellulose in fresh leaves using near infrared reflectance data. J. Near Infrared Spectrosc. 1994, 2, 25–32. [Google Scholar] [CrossRef]
- Bolster, K.L.; Martin, M.E.; Aber, J.D. Determination of carbon fraction and nitrogen concentration in tree foliage by near infrared reflectance: A comparison of statistical methods. Can. J. For. Res. 1996, 26, 590–600. [Google Scholar] [CrossRef]
- Gillon, D.; Joffre, R.; Ibrahima, A. Can litter decomposability be predicted by near infrared reflectance spectroscopy? Ecology 1999, 80, 175–186. [Google Scholar] [CrossRef]
- Vávřová, P.; Stenberg, B.; Karsisto, M.; Kitunen, V.; Tapania, T.; Laiho, R. Near infrared reflectance spectroscopy for characterization of plant litter quality: Towards a simpler way of predicting carbon turnover in Peatlands? In Wastewater Treatment, Plant Dynamics and Management in Constructed and Natural Wetlands; Vymazal, J., Ed.; Springer: New York, NY, USA, 2008; p. 65. [Google Scholar]
- Kim, Y.T.; Suh, S.R. Comparison of performance of models to predict hardness of tomato using spectroscopic data of reflectance and transmittance. J. Biosyst. Eng. 2008, 33, 63–68. (In Korean) [Google Scholar] [CrossRef]
- Kawano, S.; Watanabe, H.; Iwamoto, M. Determination of sugar content in intact peaches by near infrared spectroscopy. J. Jpn. Soc. Hortic. Sci. 1992, 61, 445–451. [Google Scholar] [CrossRef]
- Dull, G.G.; Leffler, R.G.; Birth, G.S.; Smittle, D.A. Instrument for non-destructive measurement of soluble solids in honeydew melons. Trans. Am. Soc. Agric. Eng. 1992, 35, 735–737. [Google Scholar] [CrossRef]
- Chung, H.-I.; Kim, H.-J. Near-infrared spectroscopy: Principles. Anal. Sci. Technol. 2000, 13, 138–151. [Google Scholar]
- Porep, J.U.; Kammerer, D.R.; Carle, R. On-line application of near infrared (NIR) spectroscopy in food production. Trends Food Sci. Technol. 2015, 46, 211–230. [Google Scholar] [CrossRef]
- Rinnan, A.; Berg, F.; van den Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Sarathjith, M.C.; Das, B.S.; Wani, S.P.; Sahrawat, K.L. Variable indicators for optimum wavelength selection in diffuse reflectance spectroscopy of soils. Geoderma 2016, 267, 1–9. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, H.; Liu, F.; He, Y. Application of near-infrared hyperspectral imaging with variable selection methods to determine and visualize caffeine content of coffee beans. Food Bioprocess Technol. 2017, 10, 213–221. [Google Scholar] [CrossRef]
- Fernández Pierna, J.A.; Abbas, O.; Baeten, V.; Dardenne, P. A backward variable selection method for PLS regression (BVSPLS). Anal. Chim. Acta 2009, 642, 89–93. [Google Scholar] [CrossRef] [PubMed]
- Kamruzzaman, M.; ElMasry, G.; Sun, D.-W.; Allen, P. Non-destructive assessment of instrumental and sensory tenderness of lamb meat using NIR hyperspectral imaging. Food Chem. 2013, 141, 389–396. [Google Scholar] [CrossRef] [PubMed]
- Kandpal, L.M.; Lohumi, S.; Kim, M.S.; Kang, J.-S.; Cho, B.-K. Near-Infrared hyperspectral imaging system coupled with multivariate methods to predict viability and vigor in muskmelon seeds. Sens. Actuators B Chem. 2016, 229, 534–544. [Google Scholar] [CrossRef]
- Zhang, L.; Garcia-Munoz, S. A comparison of different methods to estimate prediction uncertainty using Partial Least Squares (PLS): A practitioner’s perspective. Chem. Intell. Lab. Syst. 2009, 97, 152–158. [Google Scholar] [CrossRef]
- De Almeida, M.R.; Correa, D.N.; Rocha, W.F.C.; Scafi, F.J.O.; Poppi, R.J. Discrimination between authentic and counterfeit banknotes using Raman spectroscopy and PLS-DA with uncertainty estimation. Microchem. J. 2013, 109, 170–177. [Google Scholar] [CrossRef]
- Van der Voet, H. Pseudo-degrees of freedom for complex predictive models: The example of partial least squares. J. Chem. 1999, 13, 195–208. [Google Scholar] [CrossRef]
- Anderson, C.M.; Bro, R. Variable selection in regression-a tutorial. J. Chem. 2010, 24, 728–737. [Google Scholar] [CrossRef]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in partial least squares regression. Chem. Intell. Lab. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Bickel, P.J.; Freedman, D.A. Some asymptotic theory for the bootstrap. Ann. Stat. 1981, 9, 1196–1217. [Google Scholar] [CrossRef]
- Lazraq, A.; Clérouxb, R.; Gauchic, J.-P. Selecting both latent and explanatory variables in the PLS1 regression model. Chem. Intell. Lab. 2003, 66, 117–126. [Google Scholar] [CrossRef]
- Nørgaard, L.; Saudland, A.; Wagner, J.; Nielsen, J.P.; Munck, L.; Engelsen, S.B. Interval partial least-squares regression (iPLS): A comparative chemometric study with an example from near-infrared spectroscopy. Appl. Spectrosc. 2000, 54, 413–419. [Google Scholar] [CrossRef]
- Collins, J.R. Change in the infra-red absorption spectrum of water with temperature. Phys. Rev. 1925, 26, 771–779. [Google Scholar] [CrossRef]








| Preprocessing Method | LVs | Calibration | Validation | Test | |||
|---|---|---|---|---|---|---|---|
| Rc2 | RMSEc | Rv2 | RMSEv | Rt2 | RMSEt | ||
| Raw data | 9 | 0.930 | 12.757 | 0.920 | 19.041 | 0.884 | 19.170 |
| SG smoothing | 8 | 0.918 | 13.848 | 0.915 | 19.571 | 0.897 | 18.103 |
| SG-1st derivative | 6 | 0.918 | 13.882 | 0.925 | 18.376 | 0.883 | 19.259 |
| SG-2nd derivative | 6 | 0.937 | 12.114 | 0.913 | 19.792 | 0.840 | 22.506 |
| MSC | 8 | 0.926 | 13.132 | 0.933 | 17.432 | 0.914 | 16.482 |
| SNV | 8 | 0.927 | 13.069 | 0.943 | 16.106 | 0.915 | 16.426 |
| Max. normalization | 7 | 0.920 | 13.699 | 0.938 | 16.797 | 0.922 | 15.711 |
| Mean normalization | 9 | 0.926 | 13.149 | 0.926 | 18.308 | 0.892 | 18.479 |
| Range normalization | 7 | 0.922 | 13.535 | 0.931 | 17.722 | 0.920 | 15.970 |
| Method | LVs | No. of Variables | Calibration | Validation | Test | ||||
|---|---|---|---|---|---|---|---|---|---|
| Rc2 | RMSEc | Rv2 | RMSEv | Rt2 | RMSEt | ||||
| Full PLSR | 7 | 804 | 0.920 | 13.699 | 0.938 | 16.797 | 0.922 | 15.711 | |
| iPLS | 7 | 150 | 0.900 | 17.825 | 0.930 | 17.825 | 0.918 | 16.115 | |
| VIP | v = 0.7 | 7 | 316 | 0.924 | 13.391 | 0.934 | 17.276 | 0.923 | 15.597 |
| v = 1.0 | 7 | 203 | 0.905 | 20.131 | 0.910 | 20.131 | 0.918 | 16.130 | |
| v = 1.5 | 7 | 150 | 0.909 | 14.620 | 0.926 | 18.314 | 0.920 | 15.916 | |
| v = 2.0 | 7 | 40 | 0.884 | 16.522 | 0.853 | 25.818 | 0.859 | 21.167 | |
| Boots-trap | c = 1.0 | 7 | 305 | 0.919 | 13.795 | 0.941 | 16.392 | 0.927 | 15.164 |
| c = 1.3 | 7 | 192 | 0.916 | 14.012 | 0.940 | 16.472 | 0.924 | 15.526 | |
| c = 1.6 | 7 | 106 | 0.909 | 14.586 | 0.929 | 17.954 | 0.918 | 16.128 | |
| c = 1.9 | 7 | 35 | 0.875 | 17.1670 | 0.884 | 22.913 | 0.878 | 19.655 | |
| Beta-peak | 6 | 63 | 0.918 | 13.834 | 0.932 | 17.494 | 0.930 | 14.905 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, G.; Hong, S.-J.; Lee, A.-Y.; Lee, Y.-E.; Im, S. Moisture Content Measurement of Broadleaf Litters Using Near-Infrared Spectroscopy Technique. Remote Sens. 2017, 9, 1212. https://doi.org/10.3390/rs9121212
Kim G, Hong S-J, Lee A-Y, Lee Y-E, Im S. Moisture Content Measurement of Broadleaf Litters Using Near-Infrared Spectroscopy Technique. Remote Sensing. 2017; 9(12):1212. https://doi.org/10.3390/rs9121212
Chicago/Turabian StyleKim, Ghiseok, Suk-Ju Hong, Ah-Yeong Lee, Ye-Eun Lee, and Sangjun Im. 2017. "Moisture Content Measurement of Broadleaf Litters Using Near-Infrared Spectroscopy Technique" Remote Sensing 9, no. 12: 1212. https://doi.org/10.3390/rs9121212
APA StyleKim, G., Hong, S. -J., Lee, A. -Y., Lee, Y. -E., & Im, S. (2017). Moisture Content Measurement of Broadleaf Litters Using Near-Infrared Spectroscopy Technique. Remote Sensing, 9(12), 1212. https://doi.org/10.3390/rs9121212