Pre-Launch JPSS-2 VIIRS Response versus Scan Angle Characterization
Abstract
:1. Introduction
2. Overview
2.1. VIIRS Overview
2.2. Testing Overview
3. Methodology
3.1. Reflective Bands
3.2. Thermal Bands
3.3. Atmospheric Correction
3.4. Uncertainty
3.5. RVS Model
4. Results
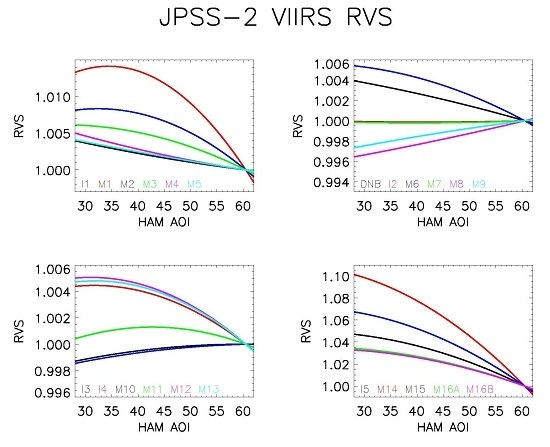
4.1. Reflective Band Performance
4.2. Thermal Band Performance
4.3. Atmospheric Correction
4.4. Uncertainty
4.5. Model Validity
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- McClain, C.; Hooker, S.; Feldman, G.; Bontempi, P. Satellite Data for Ocean Biology, Biogeochemistry, and Climate Research. EOS 2006, 87, 337–339. [Google Scholar] [CrossRef]
- King, M.D.; Menzel, W.P.; Kaufman, Y.J.; Tanre, D.; Gao, B.C.; Platnick, S.; Ackerman, S.A.; Remer, L.A.; Pincus, R.; Hubanks, P.A. Cloud and aerosol and water vapor properties, precipitable water, and profiles of temperature and humidity from MODIS. IEEE Trans. Geosci. Remote Sens. 2003, 41, 442–458. [Google Scholar] [CrossRef]
- Justice, C.O.; Vermote, E.; Townshend, J.R.G.; Defries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; et al. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef]
- Xiong, X.; Butler, J.; Chiang, K.; Efremova, B.; Fulbright, J.; Lei, N.; McIntire, J.; Oudrari, H.; Wang, Z.; Wu, A. Assessment of S-NPP VIIRS On-Orbit Radiometric Calibration and Performance. Remote Sens. 2016, 8, 84. [Google Scholar] [CrossRef]
- Cao, C.; De Luccia, F.; Xiong, X.; Wolfe, R.; Weng, F. Early in orbit performance of the Visible Infrared Imaging Radiometer Suite (VIIRS) onboard the Suomi National Polar-Orbiting Partnership (S-NPP) satellite. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1142–1156. [Google Scholar] [CrossRef]
- Oudrari, H.; McIntire, J.; Xiong, X.; Butler, J.; Ji, Q.; Schwarting, T.; Lee, S.; Efremova, B. JPSS-1 VIIRS Radiometric Characterization and Calibration Based on Pre-Launch Testing. Remote Sens. 2016, 8, 41. [Google Scholar] [CrossRef]
- Oudrari, H.; McIntire, J.; Xiong, X.; Butler, J.; Lee, S.; Lei, N.; Schwarting, T.; Sun, J. Prelaunch Radiometric Characterization and Calibration of the S-NPP VIIRS Sensor. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2195–2210. [Google Scholar] [CrossRef]
- Moyer, D.; McIntire, J.; Oudrari, H.; McCarthy, J.; Xiong, X.; DeLuccia, F. JPSS-1 VIIRS Pre-Launch Response Versus Scan Angle Testing and Performance. Remote Sens. 2016, 8, 141. [Google Scholar] [CrossRef]
- McIntire, J.; Moeller, C.; Oudrari, H.; Xiong, X. Atmospheric Correction for JPSS-2 VIIRS Response versus Scan Angle Measurements. In Proceedings of the Earth Observing Systems XXII, San Diego, CA, USA, 6–10 August 2017; Volume 10402. [Google Scholar]
- McIntire, J.; Moyer, D.; Oudrari, H.; Xiong, X. Pre-Launch Radiometric Characterization of JPSS-1 VIIRS Thermal Emissive Bands. Remote Sens. 2016, 8, 47. [Google Scholar] [CrossRef]
- Lawrence, M.G. The relationship between relative humidity and the dewpoint temperature in moist air: A simple conversion and applications. Am. Meterol. Soc. 2005, 86, 225–233. [Google Scholar] [CrossRef]
- Young, J.B. Atmospheric Transmittance Effects on Calibration; Technical Report; Santa Barbara Research Center: Santa Barbara, CA, USA, 1995. [Google Scholar]
- Clough, S.A.; Shephard, M.W.; Mlawer, E.J.; Delamere, J.S.; Iacono, M.J.; Cady-Pereira, K.; Boukabara, S.; Brown, P.D. Atmospheric radiative transfer modeling: A summary of the AER codes, Short Communication. J. Quant. Spectrosc. Radiat. Transf. 2005, 91, 233–244. [Google Scholar] [CrossRef]
- Clough, S.A.; Iacono, M.J.; Moncet, J.L. Line-by-line calculation of atmospheric fluxes and cooling rates: Application to water vapor. J. Geophys. Res. 1992, 97, 15761–15785. [Google Scholar] [CrossRef]
- Taylor, J.R. An Introduction to Error Analysis; University Science Books: Sausalito, CA, USA, 1997. [Google Scholar]
- Taylor, B.N.; Kuyatt, C.E. Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 1994.








| Band | Center (nm) | Band | Center (nm) | Band | Center (nm) |
|---|---|---|---|---|---|
| M1 | 412 | M7 | 865 | I4 | 3740 |
| M2 | 445 | I2 | 865 | M13 | 4050 |
| M3 | 488 | M8 | 1240 | M14 | 8550 |
| M4 | 555 | M9 | 1378 | M15 | 10,763 |
| I1 | 640 | M10 | 1610 | I5 | 11,450 |
| M5 | 672 | I3 | 1610 | M16A | 12,013 |
| DNB | 700 | M11 | 2250 | M16B | 12,013 |
| M6 | 746 | M12 | 3700 |
| Reflective | Thermal | ||||
|---|---|---|---|---|---|
| Collection | Scan Angle (Degrees) | HAM AOI (Degrees) | Collection | Scan Angle (Degrees) | HAM AOI (Degrees) |
| 1 | −66.3 | 60.7 | 1 | −8.0 | 38.5 |
| 2 | −8.7 | 38.8 | 2 | −66.2 | 60.7 |
| 3 | −38.7 | 49.6 | 3 | 21.6 | 30.9 |
| 4 | 5.3 | 34.6 | 4 | −45.5 | 52.2 |
| 5 | −45.7 | 52.3 | 5 | 5.5 | 34.5 |
| 6 | −8.7 | 38.8 | 6 | −8.0 | 38.5 |
| 7 | −55.7 | 56.4 | 7 | −55.9 | 56.4 |
| 8 | 21.3 | 30.9 | 8 | −20.5 | 42.8 |
| 9 | −30.7 | 46.5 | 9 | −38.5 | 49.5 |
| 10 | −8.7 | 38.6 | 10 | −8.0 | 38.5 |
| 11 | −51.7 | 54.7 | 11 | −51.4 | 54.6 |
| 12 | 37.5 | 28.9 | 12 | 35.0 | 29.1 |
| 13 | −20.7 | 42.8 | 13 | −30.5 | 46.4 |
| 14 | 54.5 | 28.9 | 14 | −8.0 | 38.5 |
| 15 | −8.7 | 38.8 | 15 | −61.2 | 58.6 |
| 16 | 5.4 | 34.6 |
| (g/m) | T (K) | ℓ (m) |
|---|---|---|
| 2.5, 5, 7.5, | 290, 305, | 1, 3, 4.5, 6, 9, 12, 20, |
| 10, 12.5, 15 | 320 | 27.5, 35, 42.5, 50, 75 |
| Band | Uncertainty | Band | Uncertainty | Band | Uncertainty |
|---|---|---|---|---|---|
| M1 | 0.041 | M7 | 0.016 | I4 | 0.263 |
| M2 | 0.026 | I2 | 0.017 | M13 | 0.152 |
| M3 | 0.025 | M8 | 0.013 | M14 | 0.130 |
| M4 | 0.053 | M9 | 0.021 | M15 | 0.113 |
| I1 | 0.015 | M10 | 0.009 | I5 | 0.230 |
| M5 | 0.035 | I3 | 0.026 | M16A | 0.113 |
| DNB | 0.010 | M11 | 0.016 | M16B | 0.114 |
| M6 | 0.023 | M12 | 0.167 |
| Scene T | I4 | I5 | M12 | M13 | M14 | M15 | M16A | M16B |
|---|---|---|---|---|---|---|---|---|
| 190 | 0.65 | 0.43 | 0.35 | 0.40 | 0.40 | 0.23 | 0.21 | 0.21 |
| 210 | 0.71 | 0.23 | 0.38 | 0.44 | 0.18 | 0.12 | 0.12 | 0.12 |
| 230 | 0.51 | 0.14 | 0.30 | 0.23 | 0.08 | 0.06 | 0.06 | 0.06 |
| 250 | 0.15 | 0.07 | 0.08 | 0.08 | 0.04 | 0.03 | 0.03 | 0.03 |
| 270 | 0.04 | 0.04 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 |
| 290 | 0.05 | 0.07 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 |
| 310 | 0.07 | 0.10 | 0.05 | 0.04 | 0.05 | 0.05 | 0.05 | 0.05 |
| 330 | 0.08 | 0.13 | 0.05 | 0.05 | 0.06 | 0.06 | 0.06 | 0.06 |
| 345 | 0.09 | 0.15 | 0.06 | 0.06 | 0.08 | 0.07 | 0.08 | 0.08 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McIntire, J.; Moyer, D.; Chang, T.; Oudrari, H.; Xiong, X. Pre-Launch JPSS-2 VIIRS Response versus Scan Angle Characterization. Remote Sens. 2017, 9, 1300. https://doi.org/10.3390/rs9121300
McIntire J, Moyer D, Chang T, Oudrari H, Xiong X. Pre-Launch JPSS-2 VIIRS Response versus Scan Angle Characterization. Remote Sensing. 2017; 9(12):1300. https://doi.org/10.3390/rs9121300
Chicago/Turabian StyleMcIntire, Jeff, David Moyer, Tiejun Chang, Hassan Oudrari, and Xiaoxiong Xiong. 2017. "Pre-Launch JPSS-2 VIIRS Response versus Scan Angle Characterization" Remote Sensing 9, no. 12: 1300. https://doi.org/10.3390/rs9121300
APA StyleMcIntire, J., Moyer, D., Chang, T., Oudrari, H., & Xiong, X. (2017). Pre-Launch JPSS-2 VIIRS Response versus Scan Angle Characterization. Remote Sensing, 9(12), 1300. https://doi.org/10.3390/rs9121300