Comparative Study on Assimilating Remote Sensing High Frequency Radar Surface Currents at an Atlantic Marine Renewable Energy Test Site
Abstract
:1. Introduction
2. Methodology
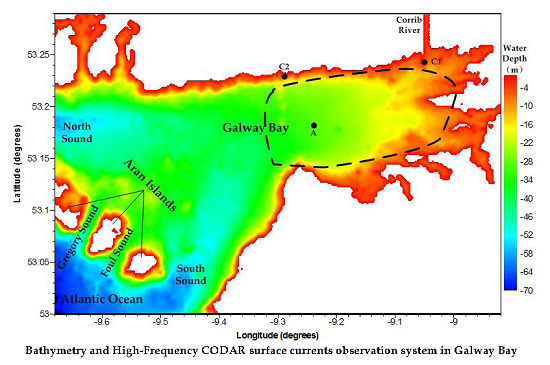
2.1. Research Domain
2.2. Numerical Model
2.3. HFR System
3. Data Assimilation Algorithms
3.1. OI DA Algorithm
3.2. DI DA Algorithm
3.3. Nudging DA Algorithm
3.4. Indirect DA Algorithm
4. Results
4.1. Hindcasting of Surface Currents
4.2. Forecasting of Surface Currents
4.3. Data Assimilation Skill Score
4.4. Average Kinetic Energy
4.5. Computational Cost
5. Discussion
6. Conclusions
- (1)
- The three-dimensional EFDC model is robust enough to frequently combine measurements from the coastal radar system into routine data assimilation algorithms in complex inshore waters strongly influenced by both tides and wind dynamics. Forecasting improvements: Each of the best data assimilation models improved the model forecasting based on the values of RMSE. The best Nudging and DI data assimilation model, which assimilated the HFR data at each model computational time step, generated the largest improvements compared with other best assimilation models (OI and IDA). The best Nudging data assimilation model was reasonably accurate and quite efficient for the research domain. Values of RMSE throughout the domain with high HFR coverage density during ≥6 h forecasting period were smaller in general when using model DI and model NDA than the RMSE values obtained using the other assimilation models and model FR.
- (2)
- All data assimilation models improved modelling performance during a hindcasting period. The OI algorithm was found to force model background states closer to HFR observations.
- (3)
- Application of those data assimilation algorithms using radar data improved forecasts of north–south surface velocity components to a greater degree than east–west surface velocity components, while model IDA degraded simulation of east–west surface velocity components. This likely resulted from using a constant wind stress over the entire computational domain.
- (4)
- Forecasting of east–west surface velocity components from all data assimilation models were closer to HFR data than model FR. Results from data assimilation models in general were comparable with each other. For the north–south surface velocity components, results from models DI, IDA and NDA were closer to HFR data than results from model OI over a ≥6 h forecasting period.
- (5)
- Distributions of RMSE values over the data assimilation domain during ≥6 h forecasting period indicate that when assimilation models are rich in HFR data these models improve forecasts, especially when using the DI or NDA algorithms.
- (6)
- DASS values decreased with time more significantly for north–south surface velocity components than east–west surface velocity components. This is probably because tidal forcing alone is more dominant in the east–west direction. Moreover, improvement in AKE values indicates that employment of data assimilation using HFR data enhanced model forecasting over the domain for a long period; models NDA and DI were shown to outperform models OI and IDA.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Paduan, J.D.; Washburn, L. High-Frequency Radar Observations of Ocean Surface Currents. Ann. Rev. Mar. Sci. 2013, 5, 115–136. [Google Scholar] [CrossRef] [PubMed]
- Dohan, K. Ocean surface currents from satellite data. J. Geophys. Res. 2017, 122, 2647–2651. [Google Scholar] [CrossRef]
- Dohan, K.; Maximenko, N. Monitoring ocean currents with satellite sensors. Oceanography 2010, 23, 94–103. [Google Scholar] [CrossRef]
- Yuan, D.; Han, W.; Hu, D. Surface Kuroshio path in the Luzon Strait area derived from satellite remote sensing data. J. Geophys. Res. 2006, 111, 63–79. [Google Scholar] [CrossRef]
- Hessner, K.; Reichert, K.; Borge, J.C.N.; Stevens, C.L.; Smith, M.J. High-resolution X-Band radar measurements of currents, bathymetry and sea state in highly inhomogeneous coastal areas. Ocean Dyn. 2014, 64, 989–998. [Google Scholar] [CrossRef]
- Gopalakrishnan, G.; Blumberg, A.F. Assimilation of HF radar-derived surface currents on tidal-timescales. J. Oper. Oceanogr. 2012, 5, 75–87. [Google Scholar] [CrossRef]
- Wanders, N.; Karssenberg, D.; Roo, A.D.; Jong, S.M.D.; Bierkens, M.F.P. The suitability of remotely sensed soil moisture for improving operational flood forecasting. Hydrol. Earth Syst. Sci. 2014, 18, 2343–2357. [Google Scholar] [CrossRef]
- Pan, X.; Li, X.; Cheng, G.; Hong, Y. Effects of 4D-Var Data Assimilation Using Remote Sensing Precipitation Products in a WRF Model over the Complex Terrain of an Arid Region River Basin. Remote Sens. 2017, 9, 963. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, F. E4DVar: Coupling an Ensemble Kalman Filter with Four-Dimensional Variational Data Assimilation in a Limited-Area Weather Prediction Model. Mon. Weather Rev. 2012, 140, 587–600. [Google Scholar] [CrossRef]
- Dobricic, S. A Sequential Variational Algorithm for Data Assimilation in Oceanography and Meteorology. Mon. Weather Rev. 2009, 137, 269–287. [Google Scholar] [CrossRef]
- Reichle, R.H.; Mclaughlin, D.B.; Entekhabi, D. Hydrologic Data Assimilation with the Ensemble Kalman Filter. Mon. Weather Rev. 2002, 130, 103–114. [Google Scholar] [CrossRef]
- Clayton, A.M.; Lorenc, A.C.; Barker, D.M. Operational implementation of a hybrid ensemble/4D-Var global data assimilation system at the Met Office. Q. J. R. Meteorol. Soc. 2013, 139, 1445–1461. [Google Scholar] [CrossRef]
- Shulman, I.; Paduan, J.D. Assimilation of HF radar-derived radials and total currents in the Monterey Bay area. Deep Sea Res. Part II 2009, 56, 149–160. [Google Scholar] [CrossRef] [Green Version]
- Marmain, J.; Molcard, A.; Forget, P.; Barth, A.; Ourmières, Y. Assimilation of HF radar surface currents to optimize forcing in the Northwestern Mediterranean Sea. Nonlinear Process. Geophys. 2014, 21, 659–675. [Google Scholar] [CrossRef] [Green Version]
- Barth, A.; Alvera-Azcárate, A.; Weisberg, R.H. Assimilation of high-frequency radar currents in a nested model of the West Florida Shelf. J. Geophys. Res. 2008, 113, 328–340. [Google Scholar] [CrossRef]
- Iermano, I.; Moore, A.M.; Zambianchi, E. Impacts of a 4-dimensional variational data assimilation in a coastal ocean model of southern Tyrrhenian Sea. J. Mar. Syst. 2016, 154, 157–171. [Google Scholar] [CrossRef]
- Dabrowski, T. A Flushing Study Analysis of Selected Irish Waterbodies. Ph.D. Thesis, National University of Ireland Galway, Galway, Ireland, 2005. [Google Scholar]
- Ren, L.; Nash, S.; Hartnett, M. Observation and modeling of tide- and wind-induced surface currents in Galway Bay. Water Sci. Eng. 2015, 8, 345–352. [Google Scholar] [CrossRef]
- O’Donncha, F.; Hartnett, M.; Nash, S.; Ren, L.; Ragnoli, E. Characterizing observed circulation patterns within a bay using HF radar and numerical model simulations. J. Mar. Syst. 2015, 142, 96–110. [Google Scholar] [CrossRef]
- Hamrick, J.M. The Environmental Fluid Dynamics Code Theory and Computation Volume 1: Hydrodynamics and Mass Transport; Tetra Tech, Inc.: Fairfax, VA, USA, 2007; p. 60. [Google Scholar]
- Baguis, P.; Roulin, E. Soil Moisture Data Assimilation in a Hydrological Model: A Case Study in Belgium Using Large-Scale Satellite Data. Remote Sens. 2017, 10, 820. [Google Scholar]
- Gauthier, P. Chaos and quadri-dimensional data assimilation: A study based on the Lorenz model. Tellus 1992, 44, 2–17. [Google Scholar] [CrossRef]
- Wen, L. Three-Dimensional Hydrodynamic Modelling in Galway Bay. Ph.D. Thesis, University College Galway, Galway, Ireland, 1995. [Google Scholar]
- Booth, D. The Water Structure and Circulation of Killary Harbour and of Galway Bay. Ph.D. Thesis, National University of Ireland, Galway, Ireland, 1975. [Google Scholar]
- Fernandes, L. A Study of the Oceanography of Galway Bay, Mid-Western Coastal Waters (Galway Bay to Bralle Bay), Shannon Estuary and the Rive Shannon Plume. Ph.D. Thesis, National University of Ireland Galway, Galway, Ireland, 1988. [Google Scholar]
- BIM. Environmental Impact Statement (EIS) for Deep Sea Fish Farm Development in Galway Bay, Co. Galway, Ireland; Irish Sea Fisheries Board: Galway, Ireland, 2012; p. 324. [Google Scholar]
- Nolan, G.D. A Study of the River Corrib Plume and its Associated Dynamics in Galway Bay during the Winter Months. Master’s Thesis, University College Galway, Galway, Ireland, 1997. [Google Scholar]
- Comerford, S.; Brophy, D. The role of wind-forcing in the distribution of larval fish in Galway Bay, Ireland. J. Mar. Assoc. U. K. 2013, 93, 471–478. [Google Scholar] [CrossRef]
- Hamrick, J.M. A Three-Dimensional Environmental Fluid Dynamics Computer Code: Therotical and Computatonal Aspects; Virginia Institute of Marine Science: Gloucester Point, VA, USA, 1992. [Google Scholar]
- Hamrick, J.M. EFDC Technical Memorandum; Tetra Tech: Fairfax, VA, USA, 2006. [Google Scholar]
- Zou, R.; Carter, S.; Shoemaker, L.; Parker, A.; Henry, T. Integrated Hydrodynamic and Water Quality Modeling System to Support Nutrient Total Maximum Daily Load Development for Wissahickon Creek, Pennsylvania. J. Environ. Eng. 2006, 132, 555–566. [Google Scholar] [CrossRef]
- Jin, K.R.; Ji, Z.G. Case Study: Modeling of Sediment Transport and Wind-Wave Impact in Lake Okeechobee. J. Hydraul. Eng. 2004, 130, 1055–1067. [Google Scholar] [CrossRef]
- O’Donncha, F.; Hartnett, M.; Nash, S. Physical and numerical investigation of the hydrodynamic implications of aquaculture farms. Aquac. Eng. 2013, 52, 14–26. [Google Scholar] [CrossRef]
- Bento, A.R.; Martinho, P.; Soares, C.G. Numerical modelling of the wave energy in Galway Bay. Renew. Energy 2015, 78, 457–466. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient Inverse Modeling of Barotropic Ocean Tides. J. Atmos. Ocean. Technol. 2002, 19, 183. [Google Scholar] [CrossRef]
- Padman, L.; Erofeeva, S. A barotropic inverse tidal model for the Arctic Ocean. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef]
- Wang, J.; Dizaji, R.; Ponsford, A.M. Analysis of clutter distribution in bistatic high frequency surface wave radar. In Proceedings of the Conference on Electrical & Computer Engineering, Niagara Falls, ON, Canada, 2–5 May 2004; Volume 3, pp. 1301–1304. [Google Scholar]
- Haus, B.K.; Wang, J.D.; Rivera, J.; Martinez-Pedraja, J.; Smith, N. Remote Radar Measurement of Shelf Currents off Key Largo, Florida, U.S.A. Estuar. Coast. Shelf Sci. 2000, 51, 553–569. [Google Scholar] [CrossRef]
- Emery, B.M.; Washburn, L.; Harlan, J.A. Evaluating radial current measurements from CODAR High-Frequency radars with moored current meters. J. Atmos. Ocean. Technol. 2004, 21, 1259–1271. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar]
- Ren, L.; Nash, S.; Hartnett, M. Forecasting of Surface Currents via Correcting Wind Stress with Assimilation of High-Frequency Radar Data in a Three-Dimensional Model. Adv. Meteorol. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Marmorino, G.O.; Shay, L.K.; Haus, B.K.; Handler, R.A.; Graber, H.C.; Horne, M.P. An EOF analysis of HF Doppler radar current measurements of the Chesapeake Bay buoyant outflow. Cont. Shelf Res. 1999, 19, 271–288. [Google Scholar] [CrossRef]
- Harlan, J.; Terrill, E.; Hazard, L.; Keen, C.; Barrick, D.; Whelan, C.; Howden, S.; Kohut, J. The Intergrated Ocean Observing System High-Frequency Radar Network: Status and Local, Regional and National Applications. Mar. Technol. Soc. J. 2010, 44, 122–132. [Google Scholar] [CrossRef]
- Tinis, S.W.; Hodgins, D.O.; Fingas, M. Assimilation of Radar Measured Surface Current Fields into a Numerical Model for Oil Spill Modelling. Spill Sci. Technol. Bull. 1996, 3, 247–251. [Google Scholar] [CrossRef]
- Abascal, A.J.; Castanedo, S.; Medina, R.; Losada, I.J.; Alvarea-Fanjul, E. Application of HF radar currents to oil spill modelling. Mar. Pollut. Bull. 2009, 58, 238–248. [Google Scholar] [CrossRef] [PubMed]
- Bellomo, L.; Griffa, A.; Cosoli, S.; Falco, P.; Gerin, R.; Iermano, I.; Kalampokis, A.; Kokkini, Z.; Magaldi, M.G.; Mamoutos, I.; et al. Toward an integrated HF radar network in the Mediterranean Sea to improve search and rescue and oil spill response: The TOSCA project experience. J. Oper. Oceanogr. 2015, 8, 95–107. [Google Scholar] [CrossRef]
- Breivik, Ø.; Sætra, Ø. Real time assimilation of HF radar currents into a coastal ocean model. J. Mar. Syst. 2001, 28, 161–182. [Google Scholar] [CrossRef]
- Vandenbulcke, L.; Beckers, J.-M.; Barth, A. Correction of inertial oscillations by assimilation of HF radar data in a model of the Ligurian Sea. Ocean Dyn. 2017, 67, 117–135. [Google Scholar] [CrossRef]
- Isern-Fontanet, J.; Ballabrera-Poy, J.; Turiel, A.; Garcia-Ladona, E. Retrieval and assimilation of velocities at the ocean surface. Nonlinear Process. Geophys. 2017, 1–38. [Google Scholar] [CrossRef]
- Ma, J.; Qin, S. Recent advances and development of data assimilation algorithms. Adv. Earth Sci. 2012, 27, 747–757. [Google Scholar]
- Sepúlveda, H.H.; Marchesiello, P.; Li, Z. Oceanic data assimilation study in northern Chile: Use of a 3DVAR method. Latin Am. J. Aquat. Res. 2013, 41, 570–575. [Google Scholar]
- Ren, L.; Nash, S.; Hartnett, M. Data Assimilation with High-Frequency (HF) Radar Surface Currents at a Marine Renewable Energy Test Site. In Renewable Energies Offshore; Soares, C.G., Ed.; CRC Press: London, UK, 2015; Chapter 24; pp. 189–193. [Google Scholar]
- Ren, L.; Hartnett, M. Sensitivity analysis of a data assimilation technique for hindcasting and forecasting hydrodynamics of a complex coastal water body. Comput. Geosci. 2016, 99, 81–90. [Google Scholar] [CrossRef]
- Ren, L.; Hartnett, M. Hindcasting and Forecasting of Surface Flow Fields through Assimilating High Frequency Remotely Sensing Radar Data. Remote Sens. 2017, 9, 1–22. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Shamshirband, S.; Petković, D. Adaptive neuro-fuzzy approach for solar radiation prediction in Nigeria. Renew. Sustain. Energy Rev. 2015, 51, 1784–1791. [Google Scholar] [CrossRef]
- Daley, R. Atmospheric Data Analysis; Cambridge University Press: Cambridge, UK, 1993; p. 457. [Google Scholar]
- Martin, M.J.; Hines, A.; Bell, M.J. Data assimilation in the FOAM operational short-range ocean forecasting system: A description of the scheme and its impact. Q. J. R. Meteorol. Soc. 2007, 133, 981–995. [Google Scholar] [CrossRef]
- Ren, L.; Hartnett, M.; Nash, S. Sensitivity tests of direct insertion data assimilation with pseudo measurements. Int. J. Comput. Commun. Eng. 2014, 3, 460–463. [Google Scholar] [CrossRef]
- Fan, S.; Oey, L.-Y.; Hamilton, P. Assimilation of drifter and satellite data in a model of the Northeastern Gulf of Mexico. Cont. Shelf Res. 2004, 24, 1001–1013. [Google Scholar] [CrossRef]
- Lin, X.H.; Oey, L.Y.; Wang, D.P. Altimetry and drifter data assimilations of loop current and eddies. J. Geophys. Res. 2007, 112, 395–412. [Google Scholar] [CrossRef]
- Gopalakrishnan, G. Surface Current Observations Using High Frequency Radar and Its Assimilation into the New York Harbor Observing and Prediction System. Ph.D. Thesis, Stevens Institute of Technology, Hoboken, NJ, USA, 2008. [Google Scholar]
- Lewis, J.K.; Shulman, I.; Blumberg, A.F. Assimilation of Doppler radar current data into numerical ocean models. Cont. Shelf Res. 1998, 18, 541–559. [Google Scholar] [CrossRef]
- Toba, Y. Local balance in the air-sea boundary processes. J. Oceanogr. Soc. Jpn. 1973, 29, 209–220. [Google Scholar] [CrossRef]
- Thiebaux, H.J. Anisotropic Correction Functions for Objective Analysis. Mon. Weather Rev. 1976, 104, 994–1002. [Google Scholar] [CrossRef]
- Ragnoli, E.; Zhuk, S.; O’Donncha, F.; Suits, F.; Hartnett, M. An Optimal Interpolation Scheme for Assimilation of HF Radar Current Data into a Numerical Ocean Model. In Proceedings of the Oceans, Hampton Roads, VA, USA, 14–19 October 2012; pp. 1–5. [Google Scholar]









| Model | RMSE (u) (cm/s) | RMSE (v) (cm/s) |
|---|---|---|
| FR | 6.46 | 6.50 |
| OI | 1.48 | 0.96 |
| NDA | 5.65 | 4.61 |
| IDA | 6.18 | 6.20 |
| Model | East–West Component (u) | North–South Component (v) | ||
|---|---|---|---|---|
| + 0–3 h | + 4–6 h | + 0–3 h | + 4–6 h | |
| DI | 0.20 | 2.30 | 0.47 | 0.17 |
| OI | 0.28 | 0.15 | 0.09 | −0.02 |
| NDA | 0.20 | 0.33 | 0.47 | 0.18 |
| IDA | −0.13 | 0.15 | 0.34 | 0.12 |
| Model | FR vs. CODAR | DI vs. CODAR | OI vs. CODAR | NDA vs. CODAR | IDA vs. CODAR |
|---|---|---|---|---|---|
| Cor(AKE) | 0.52 | 0.59 | 0.54 | 0.59 | 0.54 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, L.; Hartnett, M. Comparative Study on Assimilating Remote Sensing High Frequency Radar Surface Currents at an Atlantic Marine Renewable Energy Test Site. Remote Sens. 2017, 9, 1331. https://doi.org/10.3390/rs9121331
Ren L, Hartnett M. Comparative Study on Assimilating Remote Sensing High Frequency Radar Surface Currents at an Atlantic Marine Renewable Energy Test Site. Remote Sensing. 2017; 9(12):1331. https://doi.org/10.3390/rs9121331
Chicago/Turabian StyleRen, Lei, and Michael Hartnett. 2017. "Comparative Study on Assimilating Remote Sensing High Frequency Radar Surface Currents at an Atlantic Marine Renewable Energy Test Site" Remote Sensing 9, no. 12: 1331. https://doi.org/10.3390/rs9121331
APA StyleRen, L., & Hartnett, M. (2017). Comparative Study on Assimilating Remote Sensing High Frequency Radar Surface Currents at an Atlantic Marine Renewable Energy Test Site. Remote Sensing, 9(12), 1331. https://doi.org/10.3390/rs9121331