Limited Effects of Water Absorption on Reducing the Accuracy of Leaf Nitrogen Estimation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Spectral Measurements and Chemical Analysis
2.3. Water Removal Technique
2.4. Correlation Analysis
- Calculate the species-specific R2 space according to the spectral index space and area-based LNC;
- Extract regions of interest (ROI) from the entire spectral index space. Members in the spectral index space who satisfy were extracted. is the maximum value in the R2 space, and TP is the specified top percentile which represents the value range near . The equation means spectral indices, whose R2 with area-based LNC lies in the value range near , will be extracted. The values of the extracted members in the spectral index space were assigned 1 while others were assigned 0 in a mask file.
- Add up the values in the mask files of the three species. The spectra area with the summation of values from mask files equal to 3 are thought to be able to estimate LNC for all species.
3. Results and Discussion
3.1. Inversion Accuracy of PROSPECT5 for the Maize Dataset
3.2. Responses of Measured, Simulated, and Water-Removed Spectra to Area-Based LNC
3.3. Water Absorption Did Not Degrade the Performance of the Optimal Nitrogen-Related Spectral Index
3.4. Water Absorption Did Not Reduce the Accuracy of PLSR
3.5. Uncertainties
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vitousek, P.M.; Howarth, R.W. Nitrogen limitation on land and in the sea: How can it occur? Biogeochemistry 1991, 13, 87–115. [Google Scholar] [CrossRef]
- Reich, P.B.; Hobbie, S.E.; Lee, T.; Ellsworth, D.S.; West, J.B.; Tilman, D.; Knops, J.M.; Naeem, S.; Trost, J. Nitrogen limitation constrains sustainability of ecosystem response to CO2. Nature 2006, 440, 922–925. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Su, B.; Currie, W.S.; Dukes, J.S.; Finzi, A.; Hartwig, U.; Hungate, B.; McMurtrie, R.E.; Oren, R.; Parton, W.J. Progressive nitrogen limitation of ecosystem responses to rising atmospheric carbon dioxide. BioScience 2004, 54, 731–739. [Google Scholar] [CrossRef]
- Hungate, B.A.; Dukes, J.S.; Shaw, M.R.; Luo, Y.; Field, C.B. Nitrogen and climate change. Science 2003, 302, 1512–1513. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.R. Photosynthesis and nitrogen relationships in leaves of c3 plants. Oecologia 1989, 78, 9–19. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Liu, M.; Wu, L. Random forest algorithm and regional applications of spectral inversion model for estimating canopy nitrogen concentration in rice. J. Remote Sens. 2014, 18, 934–945. [Google Scholar]
- Jacquemoud, S.; Baret, F. Prospect: A model of leaf optical-properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Dawson, T.P.; Curran, P.J.; Plummer, S.E. Liberty—Modeling the effects of leaf biochemical concentration on reflectance spectra. Remote Sens. Environ. 1998, 65, 50–60. [Google Scholar] [CrossRef]
- Yamada, N.; Fujimura, S. Nondestructive measurement of chlorophyll pigment content in plant leaves from three-color reflectance and transmittance. Appl. Opt. 1991, 30, 3964–3973. [Google Scholar] [CrossRef] [PubMed]
- Fukshansky, L.; Fukshansky-Kazarinova, N.; Remisowsky, A.M.V. Estimation of optical parameters in a living tissue by solving the inverse problem of the multiflux radiative transfer. Appl. Opt. 1991, 30, 3145–3153. [Google Scholar] [CrossRef] [PubMed]
- Maheu, B.; Letoulouzan, J.N.; Gouesbet, G. Four-flux models to solve the scattering transfer equation in terms of lorenz-mie parameters. Appl. Opt. 1984, 23, 3353–3362. [Google Scholar] [CrossRef] [PubMed]
- Ganapol, B.D.; Johnson, L.F.; Hammer, P.D.; Hlavka, C.A.; Peterson, D.L. Leafmod: A new within-leaf radiative transfer model. Remote Sens. Environ. 1998, 63, 182–193. [Google Scholar] [CrossRef]
- Stitt, M.; Schulze, D. Does rubisco control the rate of photosynthesis and plant growth? An exercise in molecular ecophysiology. Plant Cell Environ. 1994, 17, 465–487. [Google Scholar] [CrossRef]
- Takashima, T.; Hikosaka, K.; Hirose, T. Photosynthesis or persistence: Nitrogen allocation in leaves of evergreen and deciduous quercus species. Plant Cell Environ. 2004, 27, 1047–1054. [Google Scholar] [CrossRef]
- Wang, Z.; Skidmore, A.K.; Darvishzadeh, R.; Heiden, U.; Heurich, M.; Wang, T. Leaf nitrogen content indirectly estimated by leaf traits derived from the prospect model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3172–3182. [Google Scholar] [CrossRef]
- Shi, T.; Wang, J.; Liu, H.; Wu, G. Estimating leaf nitrogen concentration in heterogeneous crop plants from hyperspectral reflectance. IJRS 2015, 36, 4652–4667. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, S.; Shi, H.; Huang, K.; Zhou, L. An evaluation of spaceborne imaging spectrometry for estimation of forest canopy nitrogen concentration in a subtropical conifer plantation of southern china. J. Resour. Ecol. 2014, 5, 1–10. [Google Scholar]
- Tian, Y.; Gu, K.; Chu, X.; Yao, X.; Cao, W.; Zhu, Y. Comparison of different hyperspectral vegetation indices for canopy leaf nitrogen concentration estimation in rice. Plant Soil 2014, 376, 193–209. [Google Scholar] [CrossRef]
- Quemada, M.; Gabriel, J.L.; Zarco-Tejada, P. Airborne hyperspectral images and ground-level optical sensors as assessment tools for maize nitrogen fertilization. Remote Sens. 2014, 6, 2940–2962. [Google Scholar] [CrossRef]
- Inoue, Y.; Sakaiya, E.; Zhu, Y.; Takahashi, W. Diagnostic mapping of canopy nitrogen content in rice based on hyperspectral measurements. Remote Sens. Environ. 2012, 126, 210–221. [Google Scholar] [CrossRef]
- Hansen, P.; Schjoerring, J. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Eitel, J.U.H.; Long, D.S.; Gessler, P.E.; Smith, A.M.S. Using in-situ measurements to evaluate the new rapideye™ satellite series for prediction of wheat nitrogen status. IJRS 2007, 28, 4183–4190. [Google Scholar]
- Muharam, F.M.; Maas, S.J.; Bronson, K.F.; Delahunty, T. Estimating cotton nitrogen nutrition status using leaf greenness and ground cover information. Remote Sens. 2015, 7, 7007–7028. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Asner, G.P.; Ollinger, S.V.; Martin, M.E.; Wessman, C.A. Characterizing canopy biochemistry from imaging spectroscopy and its application to ecosystem studies. Remote Sens. Environ. 2009, 113, S78–S91. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide dynamic range vegetation index for remote quantification of biophysical characteristics of vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Knyazikhin, Y.; Schull, M.A.; Stenberg, P.; Mõttus, M.; Rautiainen, M.; Yang, Y.; Marshak, A.; Carmona, P.L.; Kaufmann, R.K.; Lewis, P. Hyperspectral remote sensing of foliar nitrogen content. PNAS 2013, 110, E185–E192. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, M.K.; Ollinger, S.V.; Hollinger, D.Y.; Wicklein, H.F.; Richardson, A.D. Canopy-scale relationships between foliar nitrogen and albedo are not observed in leaf reflectance and transmittance within temperate deciduous tree species. Botany 2011, 89, 491–497. [Google Scholar] [CrossRef]
- Ollinger, S.; Richardson, A.; Martin, M.; Hollinger, D.; Frolking, S.; Reich, P.; Plourde, L.; Katul, G.; Munger, J.; Oren, R. Canopy nitrogen, carbon assimilation, and albedo in temperate and boreal forests: Functional relations and potential climate feedbacks. PNAS 2008, 105, 19336–19341. [Google Scholar] [CrossRef] [PubMed]
- Pellissier, P.A.; Ollinger, S.V.; Lepine, L.C.; Palace, M.W.; McDowell, W.H. Remote sensing of foliar nitrogen in cultivated grasslands of human dominated landscapes. Remote Sens. Environ. 2015, 167, 88–97. [Google Scholar] [CrossRef]
- Mitchell, J.J.; Glenn, N.F.; Sankey, T.T.; Derryberry, D.R.; Germino, M.J. Remote sensing of sagebrush canopy nitrogen. Remote Sens. Environ. 2012, 124, 217–223. [Google Scholar] [CrossRef]
- Martin, M.; Plourde, L.; Ollinger, S.; Smith, M.-L.; McNeil, B. A generalizable method for remote sensing of canopy nitrogen across a wide range of forest ecosystems. Remote Sens. Environ. 2008, 112, 3511–3519. [Google Scholar] [CrossRef]
- Martin, M.E.; Aber, J.D. High spectral resolution remote sensing of forest canopy lignin, nitrogen, and ecosystem processes. Ecol. Appl. 1997, 7, 431–443. [Google Scholar] [CrossRef]
- Wessman, C.A.; Aber, J.D.; Peterson, D.L.; Melillo, J.M. Foliar analysis using near infrared reflectance spectroscopy. Can. J. For. Res. 1988, 18, 6–11. [Google Scholar] [CrossRef]
- Wessman, C.A.; Aber, J.D.; Peterson, D.L.; Melillo, J.M. Remote sensing of canopy chemistry and nitrogen cycling in temperate forest ecosystems. Nature 1988, 335, 154–156. [Google Scholar] [CrossRef]
- Feilhauer, H.; Asner, G.P.; Martin, R.E. Multi-method ensemble selection of spectral bands related to leaf biochemistry. Remote Sens. Environ. 2015, 164, 57–65. [Google Scholar] [CrossRef]
- Zhao, K.; Valle, D.; Popescu, S.; Zhang, X.; Mallick, B. Hyperspectral remote sensing of plant biochemistry using bayesian model averaging with variable and band selection. Remote Sens. Environ. 2013, 132, 102–119. [Google Scholar] [CrossRef]
- Kalacska, M.; Lalonde, M.; Moore, T.R. Estimation of foliar chlorophyll and nitrogen content in an ombrotrophic bog from hyperspectral data: Scaling from leaf to image. Remote Sens. Environ. 2015, 169, 270–279. [Google Scholar] [CrossRef]
- Curran, P.J. Remote sensing of foliar chemistry. Remote Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
- Axelsson, C.; Skidmore, A.K.; Schlerf, M.; Fauzi, A.; Verhoef, W. Hyperspectral analysis of mangrove foliar chemistry using plsr and support vector regression. IJRS 2013, 34, 1724–1743. [Google Scholar] [CrossRef]
- Serrano, L.; Penuelas, J.; Ustin, S.L. Remote sensing of nitrogen and lignin in mediterranean vegetation from aviris data: Decomposing biochemical from structural signals. Remote Sens. Environ. 2002, 81, 355–364. [Google Scholar] [CrossRef]
- Gao, B.-C.; Goetz, A.F.H. Extraction of dry leaf spectral features from reflectance spectra of green vegetation. Remote Sens. Environ. 1994, 47, 369–374. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C.; Hill, J.; Buddenbaum, H.; Werner, W.; Schüler, G. Retrieval of chlorophyll and nitrogen in norway spruce (picea abies l. Karst.) using imaging spectroscopy. IJAEO 2010, 12, 17–26. [Google Scholar] [CrossRef]
- Ramoelo, A.; Skidmore, A.K.; Schlerf, M.; Mathieu, R.; Heitkönig, I.M.A. Water-removed spectra increase the retrieval accuracy when estimating savanna grass nitrogen and phosphorus concentrations. IJPRS 2011, 66, 408–417. [Google Scholar] [CrossRef]
- Allen, W.A.; Gausman, H.W.; Richardson, A.J.; Thomas, J.R. Interaction of isotropic light with a compact plant leaf. J. Opt. Soc. Am. 1969, 59, 1376–1379. [Google Scholar] [CrossRef]
- Lichtenthaler, H.K. [34] chlorophylls and carotenoids: Pigments of photosynthetic biomembranes. Methods Enzymol. 1987, 148, 350–382. [Google Scholar]
- Jacquemoud, S.; Ustin, S.; Verdebout, J.; Schmuck, G.; Andreoli, G.; Hosgood, B. Estimating leaf biochemistry using the prospect leaf optical properties model. Remote Sens. Environ. 1996, 56, 194–202. [Google Scholar] [CrossRef]
- Baret, F.; Fourty, T. Estimation of leaf water content and specific leaf weight from reflectance and transmittance measurements. Agronomie 1997, 17, 455–464. [Google Scholar] [CrossRef]
- Fourty, T.; Baret, F.; Jacquemoud, S.; Schmuck, G.; Verdebout, J. Leaf optical properties with explicit description of its biochemical composition: Direct and inverse problems. Remote Sens. Environ. 1996, 56, 104–117. [Google Scholar] [CrossRef]
- Feret, J.-B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. Prospect-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Tsai, F.; Philpot, W. Derivative analysis of hyperspectral data. Remote Sens. Environ. 1998, 66, 41–51. [Google Scholar] [CrossRef]
- Kramer, R. Chemometric Techniques for Quantitative Analysis; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Kokaly, R.F. Investigating a physical basis for spectroscopic estimates of leaf nitrogen concentration. Remote Sens. Environ. 2001, 75, 153–161. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Clark, R.N. Spectroscopic determination of leaf biochemistry using band-depth analysis of absorption features and stepwise multiple linear regression. Remote Sens. Environ. 1999, 67, 267–287. [Google Scholar] [CrossRef]
- Bolster, K.L.; Martin, M.E.; Aber, J.D. Determination of carbon fraction and nitrogen concentration in tree foliage by near infrared reflectances: A comparison of statistical methods. Can. J. For. Res. 1996, 26, 590–600. [Google Scholar] [CrossRef]
- Hosgood, B.; Jacquemoud, S.; Andreoli, G.; Verdebout, J.; Pedrini, G.; Schmuck, G. Leaf Optical Properties Experiment 93 (lopex93); European Commision, Joint Research Center, Institute for Remote Sensing Applications Report EUR 16095 EN; European Commission, Joint Research Centre: Ispra, Italy, 1995. [Google Scholar]





| Species | Date 1 | Site | No. Samples | Area-Based LNC (g/m2) * | ||
|---|---|---|---|---|---|---|
| Min | Max | Mean | ||||
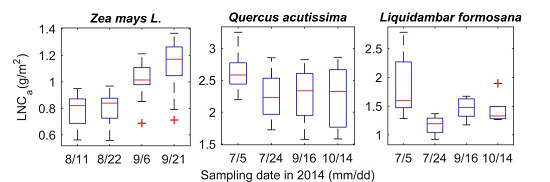
| Maize (Zea mays L.) | 8/11, 8/22, 9/6, 9/21 | NUIST | 112 | 0.56 | 1.37 | 0.96 |
| Sawtooth Oak (Quercus acutissima) | 6/24, 7/21, 9/16, 10/14 | Xiashu | 79 | 1.57 | 3.25 | 2.36 |
| Sweetgum (Liquidambar formosana) | 6/24, 7/21, 9/16, 10/14 | Xiashu | 40 | 0.92 | 2.78 | 1.49 |
| Spectra | Species | SI * | λ1 (nm) | λ2 (nm) | R2 | RMSE (g/m2) |
|---|---|---|---|---|---|---|
| Measured | Maize (Zea mays L.) | NDSI | 715 | 1750 | 0.81 | 0.09 |
| RSI | 560 | 1386 | 0.82 | 0.09 | ||
| NDSI1st | 694 | 749 | 0.80 | 0.09 | ||
| RSI1st | 1392 | 739 | 0.82 | 0.09 | ||
| Sawtooth Oak (Quercus acutissima) | NDSI | 750 | 815 | 0.44 | 0.29 | |
| RSI | 750 | 815 | 0.45 | 0.29 | ||
| NDSI1st | 561 | 1378 | 0.46 | 0.29 | ||
| RSI1st | 1378 | 561 | 0.48 | 0.28 | ||
| Sweetgum (Liquidambar formosana) | NDSI | 476 | 2235 | 0.56 | 0.27 | |
| RSI | 1446 | 476 | 0.58 | 0.27 | ||
| NDSI1st | 673 | 860 | 0.60 | 0.26 | ||
| RSI1st | 2221 | 807 | 0.60 | 0.26 | ||
| Simulated | Maize (Zea mays L.) | NDSI | 715 | 716 | 0.82 | 0.09 |
| RSI | 697 | 1381 | 0.83 | 0.08 | ||
| NDSI1st | 652 | 941 | 0.82 | 0.08 | ||
| RSI1st | 1535 | 736 | 0.83 | 0.08 | ||
| Sawtooth Oak (Quercus acutissima) | NDSI | 1533 | 1854 | 0.41 | 0.30 | |
| RSI | 1124 | 2046 | 0.41 | 0.30 | ||
| NDSI1st | 767 | 1937 | 0.50 | 0.27 | ||
| RSI1st | 771 | 1933 | 0.53 | 0.27 | ||
| Sweetgum (Liquidambar formosana) | NDSI | 2181 | 2242 | 0.44 | 0.31 | |
| RSI | 2076 | 400 | 0.45 | 0.30 | ||
| NDSI1st | 1922 | 2197 | 0.63 | 0.25 | ||
| RSI1st | 1938 | 1771 | 0.58 | 0.27 | ||
| Water-removed | Maize (Zea mays L.) | NDSI | 715 | 716 | 0.82 | 0.09 |
| RSI | 702 | 724 | 0.82 | 0.09 | ||
| NDSI1st | 578 | 583 | 0.82 | 0.09 | ||
| RSI1st | 603 | 579 | 0.82 | 0.09 | ||
| Sawtooth Oak (Quercus acutissima) | NDSI | 563 | 693 | 0.28 | 0.33 | |
| RSI | 693 | 560 | 0.28 | 0.33 | ||
| NDSI1st | 431 | 1294 | 0.35 | 0.31 | ||
| RSI1st | 431 | 1294 | 0.34 | 0.32 | ||
| Sweetgum (Liquidambar formosana) | NDSI | 782 | 1277 | 0.33 | 0.34 | |
| RSI | 400 | 1896 | 0.33 | 0.34 | ||
| NDSI1st | 430 | 1286 | 0.46 | 0.30 | ||
| RSI1st | 1032 | 865 | 0.35 | 0.33 |
| Spectra | SI * | λ1 (nm) | λ2 (nm) | ETP (%) | Maize (Zea mays L.) | Sawtooth oak (Quercus acutissima) | Sweetgum (Liquidambar formosana) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (g/m2) | R2 | RMSE (g/m2) | R2 | RMSE (g/m2) | |||||
| measured | NDSI | 615 | 705 | 34 | 0.54 | 0.17 | 0.31 | 0.19 | 0.39 | 0.17 |
| RSI | 705 | 616 | 34 | 0.55 | 0.17 | 0.31 | 0.19 | 0.38 | 0.17 | |
| NDSI1st | 699 | 1356 | 42 | 0.48 | 0.18 | 0.33 | 0.19 | 0.36 | 0.18 | |
| RSI1st | 708 | 1390 | 38 | 0.52 | 0.17 | 0.42 | 0.18 | 0.38 | 0.17 | |
| simulated | NDSI | 488 | 731 | 46 | 0.50 | 0.18 | 0.22 | 0.20 | 0.24 | 0.19 |
| RSI | 505 | 2095 | 42 | 0.49 | 0.18 | 0.24 | 0.20 | 0.26 | 0.19 | |
| NDSI1st | 699 | 1931 | 42 | 0.49 | 0.18 | 0.36 | 0.19 | 0.36 | 0.18 | |
| RSI1st | 703 | 1929 | 40 | 0.55 | 0.17 | 0.39 | 0.18 | 0.35 | 0.18 | |
| water-removed | NDSI | 420 | 734 | 34 | 0.55 | 0.17 | 0.20 | 0.21 | 0.22 | 0.20 |
| RSI | 447 | 734 | 32 | 0.56 | 0.17 | 0.20 | 0.21 | 0.23 | 0.19 | |
| NDSI1st | 565 | 1357 | 44 | 0.46 | 0.18 | 0.20 | 0.21 | 0.28 | 0.19 | |
| RSI1st | 1292 | 704 | 30 | 0.60 | 0.16 | 0.27 | 0.20 | 0.25 | 0.19 | |
| Species | Spectra | RMSEP*(g/m2) | R2 Predicted | No. Components |
|---|---|---|---|---|
| Maize (Zea mays L.) | Measured | 0.10 | 0.80 | 3 |
| Simulated | 0.09 | 0.83 | 7 | |
| Water-removed | 0.09 | 0.82 | 7 | |
| Sawtooth Oak (Quercus acutissima) | Measured | 0.28 | 0.56 | 3 |
| Simulated | 0.30 | 0.51 | 4 | |
| Water-removed | 0.35 | 0.33 | 5 | |
| Sweetgum (Liquidambar formosana) | Measured | 0.32 | 0.81 | 4 |
| Simulated | 0.32 | 0.58 | 6 | |
| Water-removed | 0.36 | 1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Chen, J.M.; Ju, W.; Qiu, F.; Zhang, Q.; Fang, M.; Chen, F. Limited Effects of Water Absorption on Reducing the Accuracy of Leaf Nitrogen Estimation. Remote Sens. 2017, 9, 291. https://doi.org/10.3390/rs9030291
Wang J, Chen JM, Ju W, Qiu F, Zhang Q, Fang M, Chen F. Limited Effects of Water Absorption on Reducing the Accuracy of Leaf Nitrogen Estimation. Remote Sensing. 2017; 9(3):291. https://doi.org/10.3390/rs9030291
Chicago/Turabian StyleWang, Jun, Jing M. Chen, Weimin Ju, Feng Qiu, Qian Zhang, Meihong Fang, and Fenge Chen. 2017. "Limited Effects of Water Absorption on Reducing the Accuracy of Leaf Nitrogen Estimation" Remote Sensing 9, no. 3: 291. https://doi.org/10.3390/rs9030291
APA StyleWang, J., Chen, J. M., Ju, W., Qiu, F., Zhang, Q., Fang, M., & Chen, F. (2017). Limited Effects of Water Absorption on Reducing the Accuracy of Leaf Nitrogen Estimation. Remote Sensing, 9(3), 291. https://doi.org/10.3390/rs9030291