Limitations and Improvements of the Leaf Optical Properties Model Leaf Incorporating Biochemistry Exhibiting Reflectance and Transmittance Yields (LIBERTY)
Abstract
:1. Introduction
2. Existence of Limitations
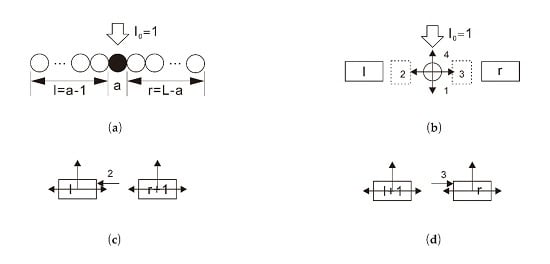
2.1. The Reflectance of Infinite Particle Medium () Is Inconsistent with the Standard Form
2.2. The Sublayer Transmittance Is Not Equal to the Theoretical Value
2.3. The Fraction of Incident Radiation Entering the Sublayer is Overestimated
3. Limitations of LIBERTY
3.1. The Directional Changes of Both Particle and Sublayer Scattering Ratios Were Not Considered
3.2. The Radiation Components Were Not Treated Satisfactorily
3.3. The Morphology of Needle Leaves Was Not Included
4. Improved Version of LIBERTY
4.1. Reassessment of the Sublayer Backscattering and Forward Scattering Ratios
4.2. Reassessment of the Sublayer Reflectance and Transmittance
4.3. The Reflectance and Transmittance of a Particle String
4.4. Differences between LIBERTY and PROSPECT
5. Materials and Methods
5.1. Ranges of Input Parameters
5.2. Sensitivity Analysis
5.3. Inter-Model Comparisons
6. Results
6.1. Sublayer Scattering Ratios Considering the Directional Changes of the Particle Scattering Ratios
6.2. The Sublayer Reflectance and Transmittance
6.3. The Global Reflectance and Transmittance
6.4. Reflectance and Transmittance of a Particle String
7. Discussion
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Notations | Connotations | Equations |
| Structural parameter, representing the number of sublayers. | Serves as a variable | |
| Relative refractive index (internal to external refractive index ratio if the external media has a lower refractive index) | Serves as a variable | |
| Absorption coefficient | Serves as a variable | |
| Particle diameter | Serves as a variable | |
| Diametrical absorbance | Serves as a variable | |
| Particle backscattering ratio | Serves as a variable | |
| Particle forward scattering ratio | Serves as a variable | |
| Particle lateral scattering ratio | ||
| Directional change coefficient of and for a sublayer | Constant, | |
| Directional change coefficient of for a sublayer | Constant, | |
| Directional change coefficient of and for a particle string | Constant, | |
| Directional change coefficient of for a particle string | Constant, | |
| External reflection coefficient for direction (supposing the external media has a lower refractive index) | where | |
| External reflectance (supposing the external media has a lower refractive index) | ||
| Internal reflectance (supposing the external media has a lower refractive index) | where | |
| One-pass transmittance inside the particle | ||
| Particle transmittance | ||
| Sublayer backscattering ratio, neglecting the directional changes of the particle scattering ratios (, and ) | ||
| Sublayer backscattering ratio, considering the directional changes of the particle scattering ratios (, and ) | Original version: Improved version: | |
| Sublayer backscattering ratio, considering the directional changes of the particle scattering ratios (, and ) | Original version: Improved version: | |
| Sublayer reflectance | Original version: Improved version: | |
| Sublayer transmittance | Original version: Improved version: | |
| Global reflectance of N homogenous layers | Where , , | |
| Global transmittance of N homogenous layers | ||
| Backscattering ratio of a particle string composed of particles, the light is assumed to incident along the string length | Where , | |
| Forward scattering ratio of a particle string composed of particles, the light is assumed to incident along the string length |
Appendix A



References
- Wang, L.; Wang, W.; Dorsey, J.; Yang, X.; Guo, B.; Shum, H.-Y. Real-time rendering of plant leaves. In ACM SIGGRAPH 2006 Courses; ACM: Boston, MA, USA, 2006; p. 5. [Google Scholar]
- Jacquemoud, S.; Ustin, L. Modeling leaf optical properties. In Photobiological Sciences Online; American Society for Photobiology: McLean, VA, USA, 2008. [Google Scholar]
- Dawson, T.P.; Curran, P.J.; Plummer, S.E. LIBERTY—Modeling the effects of leaf biochemical concentration on reflectance spectra. Remote Sens. Environ. 1998, 65, 50–60. [Google Scholar] [CrossRef]
- Melamed, N.T. Optical properties of powders. Part I. Optical absorption coefficients and the absolute value of the diffuse reflectance. Part II. Properties of luminescent powders. J. Appl. Phys. 1963, 34, 560–570. [Google Scholar] [CrossRef]
- Benford, F. Radiation in a diffusing medium. J. Opt. Soc. Am. 1946, 36, 524. [Google Scholar] [CrossRef] [PubMed]
- Moorthy, I.; Miller, J.R.; Noland, T.L. Estimating chlorophyll concentration in conifer needles with hyperspectral data: An assessment at the needle and canopy level. Remote Sens. Environ. 2008, 112, 2824–2838. [Google Scholar] [CrossRef]
- Mandelis, A.; Boroumand, F.; Bergh, H.V. Quantitative diffuse reflectance spectroscopy of large powders: The melamed model revisited. Appl. Opt. 1990, 29, 2853–2860. [Google Scholar] [CrossRef] [PubMed]
- Stokes, G.G. On the intensity of the light reflected from or transmitted through a pile of plates. Proc. R. Soc. Lond. 1860, 11, 545–556. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, J.M.; Miller, J.R.; Noland, T.L. Retrieving chlorophyll content in conifer needles from hyperspectral measurements. Can. J. Remote. Sens. 2008, 34, 296–310. [Google Scholar]
- Di Vittorio, A.V. Enhancing a leaf radiative transfer model to estimate concentrations and in vivo specific absorption coefficients of total carotenoids and chlorophylls a and b from single-needle reflectance and transmittance. Remote Sens. Environ. 2009, 113, 1948–1966. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. Prospect: A model of leaf optical-properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Feret, J.-B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. Prospect-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Simonot, L.; Hébert, M.; Hersch, R.D.; Garay, H. Ray scattering model for spherical transparent particles. J. Opt. Soc. Am. A 2008, 25, 1521–1534. [Google Scholar] [CrossRef]
- Ceccato, P.; Gobron, N.; Flasse, S.; Pinty, B.; Tarantola, S. Designing a spectral index to estimate vegetation water content from remote sensing data: Part 1: Theoretical approach. Remote Sens. Environ. 2002, 82, 188–197. [Google Scholar] [CrossRef]
- Wang, Z.; Skidmore, A.K.; Wang, T.; Darvishzadeh, R.; Hearne, J. Applicability of the prospect model for estimating protein and cellulose+ lignin in fresh leaves. Remote Sens. Environ. 2015, 168, 205–218. [Google Scholar] [CrossRef]
- Cannavó, F. Sensitivity analysis for volcanic source modeling quality assessment and model selection. Comput. Geosci. 2012, 44, 52–59. [Google Scholar] [CrossRef]
- He, W.; Yang, H. Efast method for global sensitivity analysis of remote sensing model’s parameters. Remote Sensing Technol. Appl. 2013, 28, 836–843. [Google Scholar]
- Saltelli, A.; Tarantola, S.; Chan, K.S. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Saltelli, A.; Bolado, R. An alternative way to compute fourier amplitude sensitivity test (fast). Comput. Stat. Data Anal. 1998, 26, 445–460. [Google Scholar] [CrossRef]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their monte carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Sobol, I.M. On sensitivity estimation for nonlinear mathematical models. Matematicheskoe Modelirovanie 1990, 2, 112–118. [Google Scholar]















| Input Parameters | Minimum Value | Maximum Value |
|---|---|---|
| 1.2708 | 1.5295 | |
| 0.0021 | 8.4985 | |
| 1.0927 | 3 | |
| 0 | 0.5 |
| Count | Backward * | Forward * | Reflected * | Next ** |
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 |
| PROSPECT5 | LIBERTY | Note | |
|---|---|---|---|
| Number of input parameters | 6 | 9 | |
| Number of input biochemical parameters | 5 | 6 | |
| Number of input structural parameters | 1 | 3 | |
| Incorporated absorbance | kd | Equivalent | |
| Sublayer morphology | Plate model | Compact particle model | |
| Method to calculate global reflectance and transmittance | Stokes theory | Benford theory | Essentially the same |
| Boundary | Not considered | Not considered | same |
| Special treatment of incident radiation | Yes | No |
| Models | |||
|---|---|---|---|
| LIBERTY | LIBERTYim ** | PROSPECT5 | |
| Outputs | Inputs | ||
| and | |||
| and | |||
| and | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Ju, W. Limitations and Improvements of the Leaf Optical Properties Model Leaf Incorporating Biochemistry Exhibiting Reflectance and Transmittance Yields (LIBERTY). Remote Sens. 2017, 9, 431. https://doi.org/10.3390/rs9050431
Wang J, Ju W. Limitations and Improvements of the Leaf Optical Properties Model Leaf Incorporating Biochemistry Exhibiting Reflectance and Transmittance Yields (LIBERTY). Remote Sensing. 2017; 9(5):431. https://doi.org/10.3390/rs9050431
Chicago/Turabian StyleWang, Jun, and Weimin Ju. 2017. "Limitations and Improvements of the Leaf Optical Properties Model Leaf Incorporating Biochemistry Exhibiting Reflectance and Transmittance Yields (LIBERTY)" Remote Sensing 9, no. 5: 431. https://doi.org/10.3390/rs9050431
APA StyleWang, J., & Ju, W. (2017). Limitations and Improvements of the Leaf Optical Properties Model Leaf Incorporating Biochemistry Exhibiting Reflectance and Transmittance Yields (LIBERTY). Remote Sensing, 9(5), 431. https://doi.org/10.3390/rs9050431