Extended Data-Based Mechanistic Method for Improving Leaf Area Index Time Series Estimation with Satellite Data
Abstract
:1. Introduction
2. Methodology
2.1. UDBM Model Construction
2.1.1. Theory of the Data-Based Mechanistic Modeling
2.1.2. Universal Data-Based Mechanistic Model Construction
2.2. PROSAIL Model
2.3. Ensemble Kalman Filter
3. Data
3.1. Satellite Datasets
3.2. LAI Reference Data
3.2.1. Field Data
3.2.2. LAI Reference Maps
4. Results
4.1. Estimated LAI Temporal Profile
4.2. Comparison with LAI Reference
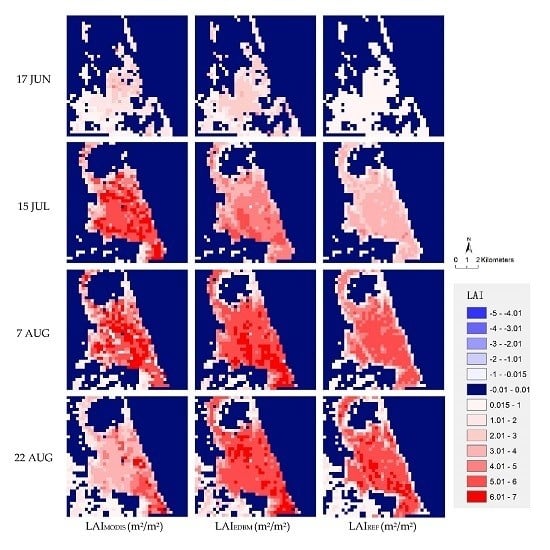
4.3. Comparison with the Reference Maps
5. Discussion
5.1. Impact of Surface Inhomogeneity
5.2. Impact of Errors Associated with the MODIS LAI Product and SG Filter on UDBM Modeling
5.3. Errors Introduced by the Radiative-Transfer Model
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Hu, J.; Tana, B.; Shabanova, N.; Creanb, K.A.; Martonchikb, J.V.; Dinerb, D.J.; Knyazikhina, Y.; Myneni, R.B. Performance of the MISR LAI and FPAR algorithm: A case study in Africa. Remote Sens. Environ. 2003, 88, 324–340. [Google Scholar] [CrossRef]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.R.; Myneni, R.B. Global data sets of vegetation leaf area index (LAI) 3g and Fraction of Photosynthetically Active Radiation (FPAR) 3g derived from Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) for the period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Weiss, M. Near Real-Time Vegetation Monitoring at Global Scale. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3473–3481. [Google Scholar] [CrossRef]
- Li, R.; Li, C.; Dong, Y.; Liu, F.; Wang, J.; Yang, X.; Pan, Y. Assimilation of Remote Sensing and Crop Model for LAI Estimation Based on Ensemble Kaiman Filter. Agric. Sci. China 2011, 10, 1595–1602. [Google Scholar] [CrossRef]
- Liu, Q.; Gu, L.; Dickinson, R.; Tian, Y.; Zhou, L.; Post, W.M. Assimilation of satellite reflectance data into a dynamical leaf model to infer seasonally varying leaf areas for climate and carbon models. J. Geophys. Res. 2008, 113, 1–7. [Google Scholar] [CrossRef]
- Dente, L.; Satalino, G.; Mattia, F.; Rinaldi, M. Assimilation of leaf area index derived from ASAR and MERIS data into CERES-Wheat model to map wheat yield. Remote Sens. Environ. 2008, 112, 1395–1407. [Google Scholar] [CrossRef]
- De Wit, A.J.W.; van Diepen, C.A. Crop model data assimilation with the Ensemble Kalman filter for improving regional crop yield forecasts. Agric. For. Meteorol. 2007, 146, 38–56. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Jiang, B.; Li, X. Real-time retrieval of Leaf Area Index from MODIS time series data. Remote Sens. Environ. 2011, 115, 97–106. [Google Scholar] [CrossRef]
- Ma, G.; Huang, J.; Wu, W.; Fan, J.; Zou, J.; Wu, S. Assimilation of MODIS-LAI into the WOFOST model for forecasting regional winter wheat yield. Math. Comput. Model. 2013, 58, 634–643. [Google Scholar] [CrossRef]
- Wang, D.W.; Wang, J.D.; Liang, S.L. Retrieving crop leaf area index by assimilation of MODIS data into a crop growth model. Sci. China Earth Sci. 2010, 53, 721–730. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Xu, X.; Zhao, C.; Jin, X.; Yang, G.; Feng, H. Assimilation of Two Variables Derived from Hyperspectral Data into the DSSAT-CERES Model for Grain Yield and Quality Estimation. Remote Sens. 2015, 7, 12400–12418. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Ali, S. A new crop yield forecasting model based on satellite measurements applied across the Indus Basin, Pakistan. Agric. Ecosyst. Environ. 2003, 94, 321–340. [Google Scholar] [CrossRef]
- Mo, X.; Liu, S.; Lin, Z.; Xu, Y.; Xiang, Y.; Mcvicar, T.R. Prediction of crop yield, water consumption and water use efficiency with a SVAT-crop growth model using remotely sensed data on the North China Plain. Ecol. Model. 2005, 183, 301–322. [Google Scholar] [CrossRef]
- Xiao, Z.; Wang, J.; Liang, S.; Zhou, H.; Li, X.; Zhang, L.; Jiao, Z.; Liu, Y.; Fu, Z. Variational retrieval of leaf area index from MODIS time series data: examples from the Heihe river basin, north-west China. Int. J. Remote Sens. 2012, 33, 730–745. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Song, J.; Wu, X. A temporally integrated inversion method for estimating leaf area index from MODIS data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2536–2545. [Google Scholar] [CrossRef]
- Jiang, B.; Liang, S.; Wang, J.; Xiao, Z. Modeling MODIS LAI time series using three statistical methods. Remote Sens. Environ. 2010, 114, 1432–1444. [Google Scholar] [CrossRef]
- Li, X.; Mao, F.; Du, H.; Zhou, G.; Xu, X.; Han, N.; Sun, S.; Gao, G.; Chen, L. Assimilating leaf area index of three typical types of subtropical forest in China from MODIS time series data based on the integrated ensemble Kalman filter and PROSAIL model. ISPRS J. Photogramm. Remote Sens. 2017, 126, 68–78. [Google Scholar] [CrossRef]
- Chen, P.; Wang, J.; Liang, S. A data-based mechanistic approach to time-series LAI modeling and estimation. J. Remote Sens. 2012, 16, 505–519. [Google Scholar]
- Young, P.C. The data-based mechanistic approach to the modelling, forecasting and control of environmental systems. Annu. Rev. Control 2006, 30, 169–182. [Google Scholar] [CrossRef]
- Young, P.C.; Ratto, M. A unified approach to environmental systems modeling. Stoch. Environ. Res. Risk Assess. 2009, 23, 1037–1057. [Google Scholar] [CrossRef]
- Guo, L.B.; Wang, J.D.; Xiao, Z.Q.; Zhou, H.M.; Song, J.L. Data-based mechanistic modelling and validation for leaf area index estimation using multi-angular remote-sensing observation time series. Int. J. Remote Sens. 2014, 35, 4655–4672. [Google Scholar] [CrossRef]
- Baret, F.; Morissette, J.T.; Fernandes, R.A.; Champeaux, J.L.; Myneni, R.B.; Chen, J.; Plummer, S.; Weiss, M.; Bacour, C.; Garrigues, S.; et al. Evaluation of the representativeness of networks of sites for the global validation and intercomparison of land biophysical products: Proposition of the CEOS-BELMANIP. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1794–1803. [Google Scholar] [CrossRef]
- Garrigues, S.; Lacaze, R.; Baret, F.; Morisette, J.T.; Weiss, M.; Nickeson, J.E.; Fernandes, R.; Plummer, S.; Shabanov, N.V.; Myneni, R.B.; et al. Validation and intercomparison of global Leaf Area Index products derived from remote sensing data. J. Geophys. Res. 2008, 113, G02028. [Google Scholar] [CrossRef]
- ImagineS. Available online: http://fp7-imagines.eu (accessed on 25 April 2017).
- Young, P.; Beck, B. The modelling and control of water quality in a river system. Automatica 1974, 10, 455–468. [Google Scholar] [CrossRef]
- Young, P. Data-based mechanistic modelling of environmental, ecological, economic and engineering systems. Environ. Model. Softw. 1998, 13, 105–122. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Weiss, M. Performances of neural networks for deriving LAI estimates from existing CYCLOPES and MODIS products. Remote Sens. Environ. 2008, 112, 2789–2803. [Google Scholar] [CrossRef]
- Brown, L.; Chen, J.M.; Leblanc, S.G.; Cihlar, J. A shortwave infrared modification to the simple ratio for LAI retrieval in boreal forests: an image and model analysis. Remote Sens. Environ. 2000, 71, 16–25. [Google Scholar] [CrossRef]
- Young, P.C. Recursive Estimation and Time-Series Analysis; Springer: Berlin, Germany, 1984. [Google Scholar]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in FORTRAN 77: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Jonsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
- Jacquemoud, S. Inversion of the PROSPECT + SAIL canopy reflectance model from AVIRIS equivalent spectra: Theoretical study. Remote Sens. Environ. 1993, 44, 281–292. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Zarco-Tejada, P.J.; Asner, G.; Francois, C.; Ustin, S.L. PROSPECT + SAIL: 15 years of use for land surface characterization. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006. [Google Scholar]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Kuusk, A. A Markov chain model of canopy reflectance. Agric. For. Meteorol. 1995, 76, 221–236. [Google Scholar] [CrossRef]
- Wang, L.; Niu, Z. Sensitivity analysis of vegetation parameters based on PROSAIL model. Remote Sens. Technol. Appl. 2014, 29, 219–223. [Google Scholar]
- Gu, C.; Du, H.; Mao, F.; Han, N.; Zhou, G.; Xu, X.; Sun, S.; Gao, G. Global sensitivity analysis of PROSAIL model parameters when simulating Moso bamboo forest canopy reflectance. Int. J. Remote Sens. 2016, 37, 5270–5286. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with a non-linear quasi-geostrophic model using Monte Carlo methods to fore- cast error statistics. J. Geophys. Res. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Evensen, G. The Ensemble Kalman Filter: theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. Trans. ASME 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Greg, W.; Gary, B. An Introduction to the Kalman Filter; Department of Computer Science, University of North Carolina at Chapel Hill: Chapel Hill, NC, USA, 2006. [Google Scholar]
- Quaife, T.; Lewis, P.; De Kauwe, M.; Williams, M.; Law, B.E.; Disney, M.; Bowyer, P. Assimilating canopy reflectance data into an ecosystem model with an Ensemble Kalman Filter. Remote Sens. Environ. 2008, 112, 1347–1364. [Google Scholar] [CrossRef]
- Vermote, E.F.; Roger, J.C.; Ray, J.P. MODIS Surface Reflectance User’s Guide. In MODIS Land Surface Reflectance Science Computing Facility; NASA/Goddard Space Flight Center: Greenbelt, MD, USA, 2015. [Google Scholar]
- Knyazikhin, Y.; Glassy, J.; Privette, J.L.; Tian, Y.; Lotsch, A.; Zhang, Y.; Wang, A.; Morisette, J.T.; Votava, P.; Myneni, R.B.; et al. MODIS Leaf Area Index (LAI) and Fraction of Photosynthetically Active Radiation Absorbed By Vegetation (FPAR) Product. In Algorithm Theoretical Basis Document; NASA: Washington, DC, USA, 1999. Available online: http://eospso.gsfc.nasa.gov/atbd/modistables.html (accessed on 26 May 2017).
- Fang, H.; Wei, S.; Liang, S. Validation of MODIS and CYCLOPES LAI products using global field measurement data. Remote Sens. Environ. 2012, 119, 43–54. [Google Scholar] [CrossRef]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Niño, F.; Weiss, M.; Samain, O.; et al. LAI, fAPAR and fCover CYCLOPES global products derived from VEGETATION. Part 1: Principles of the algorithm. Remote Sens. Environ. 2007, 110, 275–286. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of General Regression Neural Networks for Generating the GLASS Leaf Area Index Product From Time-Series MODIS Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.; Liao, A.; Cao, X.; Chen, L.; Chen, X.; He, C.; Han, G.; Peng, S.; Lu, M. Global land cover mapping at 30m resolution: A POK-based operational approach. ISPRS J. Photogramm. Remote Sens. 2015, 103, 7–27. [Google Scholar] [CrossRef]
- Pahlevan, N.; Sarkar, S.; Devadiga, S.; Wolfe, R.E.; Román, M.; Vermote, E.; Lin, G.; Xiong, X. Impact of Spatial Sampling on Continuity of MODIS-VIIRS Land Surface Reflectance Products: A Simulation Approach. IEEE Trans. Geosci. Remote Sens. 2017, 55, 183–196. [Google Scholar] [CrossRef]
- Campagnolo, M.L.; Sun, Q.; Liu, Y.; Schaaf, C.; Wang, Z.; Román, M.O. Estimating the effective spatial resolution of the operational BRDF, albedo, and nadir reflectance products from MODIS and VIIRS. Remote Sens. Environ. 2016, 175, 52–64. [Google Scholar] [CrossRef]
- Yin, G.; Li, J.; Liu, Q.; Fan, W.; Xu, B.; Zeng, Y.; Zhao, J. Regional Leaf Area Index Retrieval Based on Remote Sensing: The Role of Radiative Transfer Model Selection. Remote Sens. 2015, 7, 4604–4625. [Google Scholar] [CrossRef]








| Model | Parameters | Symbol | Values | Unit |
|---|---|---|---|---|
| Prospect | Chlorophyll content * | Cab | 30 | μg cm−2 |
| Carotenoids content | Car | 10 | μg cm−2 | |
| Total pigment content | Cbp | 0 | - | |
| Water equivalent thickness | Cw | 0.015 | cm | |
| Dry matter content * | Cm | 0.00125–0.00625 | μg cm−2 | |
| Leaf structure index * | 1–2.5 | - | ||
| Sail | Leaf area index * | LAI | 0–8 | - |
| Mean leaf angle * | ALA | 40–85 | deg | |
| Hot spot * | SL | 0.01–1 | - | |
| Soil factor | ρs | 0.2 | - | |
| Scatter light proportion | SKYL | 0.1 | - | |
| Solar zenith angle | θs | 0–90 | deg | |
| Observation zenith angle | θv | 0–90 | deg | |
| Relative azimuth angle | φsv | 0–180 | deg |
| Band Number | Band Range (nm) |
|---|---|
| 1 | 620–670 |
| 2 | 841–876 |
| 7 | 2105–2155 |
| Parameter | LAI | Cab | Cw | Cm | ALA | Ps |
|---|---|---|---|---|---|---|
| Initial value | 1.0 | 30 | 0.01 | 0.001 | 70 | 0.2 |
| Variance | 0.35 | 6 | 0.001 | 0.0001 | 9 | 0.001 |
| Site Name | Latitude | Longitude | Land Cover Type | Site Name | Latitude | Longitude | Land Cover Type |
|---|---|---|---|---|---|---|---|
| Lost Creek | 46.08 | –89.97 | Deciduous broadleaf forest | Soignes | 50.78 | 4.42 | Deciduous broadleaf forest |
| Malga Arpaco | 46.11 | 11.70 | Mixed forest | Hainich | 51.07 | 10.45 | Deciduous broadleaf forest |
| Sylvania Wilderness Area-Michigan | 46.24 | –89.34 | Mixed forest | Brasschaat (De Inslag Forest) | 51.30 | 4.52 | Deciduous broadleaf forest |
| New Brunswick-Nashwaak Lake 1 | 46.47 | –67.1 | Mixed forest | Leinefelde | 51.32 | 10.36 | Deciduous broadleaf forest |
| Neustift/Stubai Valley | 47.11 | 11.31 | Mixed forest | Sask-SSA Old Aspen | 53.62 | –106.19 | Mixed forest |
| Gilching (VALERI) | 48.08 | 11.32 | Mixed forest | BOREAS SSA Young Aspen | 53.65 | –105.32 | Mixed forest |
| Ontario-Groundhog River-Mature Boreal Mixed Wood | 48.21 | –82.15 | Mixed forest | Kannenbruch Forest | 53.78 | 10.6 | Mixed forest |
| Hesse Forest-Sarrebourg | 48.67 | 7.06 | Deciduous broadleaf forest | Whitecourt | 54.04 | –115.79 | Mixed forest |
| Vielsalm | 50.30 | 5.99 | Mixed forest | Sask-Fire 1989 | 54.25 | –105.87 | Mixed forest |
| COMPLET 160 | 50.66 | 27.89 | Mixed forest | Jarvselja (VALERI) | 58.29 | 27.26 | Mixed forest |
| Site Name | Latitude | Longitude | Land Cover Type | Site Name | Latitude | Longitude | Land Cover Type |
|---|---|---|---|---|---|---|---|
| COMPLET 163 (56.1129°N, −69.3589°W) | 56.11 | –69.35 | savannas | Quebec | 54.5 | –75.7 | shrubs |
| UCI-1998 burn site | 56.63 | –99.94 | savannas | Audubon Research Ranch-Arizona | 31.59 | –110.51 | shrubs |
| Quebec Boreal Cutover Site | 49.26 | –74.03 | savannas | Santa Rita Mesquite-Arizona | 31.82 | –110.86 | shrubs |
| COMPLET | 0.58 | 14.83 | croplands | Haouz (VALERI) | 31.65 | –7.60 | shrubs |
| COMPLET 133 | 8.57 | 19.91 | savannas | Sky Oaks-Young Stand-California | 33.37 | –116.62 | shrubs |
| Qianyanzhou | 26.73 | 115.06 | savannas | Jornada LTER-New Mexico (JRN1) | 32.59 | –106.84 | shrubs |
| Ilorin | 8.32 | 4.34 | savannas | Maricopa Agricultural Center-Arizona | 33.07 | –111.97 | croplands |
| Sardinilla Pasture | 9.30 | –79.63 | croplands | Sud-Ouest (VALERI) | 43.506 | 1.23 | croplands |
| Tonzi Ranch-California | 38.43 | –120.96 | savannas | Bondville-Illinois | 40.00 | –88.29 | croplands |
| Freeman Ranch-Grassland-Texas | 29.93 | –98.01 | savannas | Mead-irrigated maize-soybean rotation site-Nebraska | 41.16 | –96.47 | croplands |
| Site Name | Latitude | Longitude | Land Cover Types | Year | DOY | LAI |
|---|---|---|---|---|---|---|
| HARV | 42.53 | –72.17 | Mixed forest | 2000 | 170 | 5.1 |
| 2000 | 217 | 5.0 | ||||
| 2001 | 208 | 5.5 | ||||
| 2002 | 236 | 5.4 | ||||
| CHEQ | 45.95 | 90.27 | Mixed forest | 2002 | 220 | 3.05 |
| KONZ | 39.09 | –96.57 | Grasses | 2000 | 159 | 2.0 |
| 2000 | 239 | 2.0 | ||||
| 2001 | 169 | 2.9 | ||||
| 2001 | 228 | 2.5 | ||||
| Sud-Ouest | 43.51 | 1.24 | Grasses and cereal crops | 2002 | 201 | 2.3 |
| ARGO | 40.01 | –88.29 | Broadleaf crops | 2000 | 186 | 2.5 |
| 2000 | 224 | 3.6 | ||||
| Alpilles | 43.81 | 4.74 | Broadleaf crops | 2002 | 201 | 1.7 |
| Larzac | 43.94 | 3.12 | Savannahs | 2002 | 193 | 0.9 |
| Map Name | Date Match | |||
|---|---|---|---|---|
| MODIS LAI DOY | 169 | 193 | 217 | 233 |
| Reference LAI date | 17 June | 15 July | 7 August | 22 August |
| LAIMODIS (m2/m2) | LAI EDBM (m2/m2) | |
|---|---|---|
| RMSE | 1.26 | 0.50 |
| BIAS | –0.22 | 0.12 |
| MAE | 0.98 | 0.30 |
| Date (2014) | LAIMODIS (m2/m2) | LAIEDBM (m2/m2) | LAIREF (m2/m2) |
|---|---|---|---|
| 17 June | 0.44 | 0.59 | 0.30 |
| 15 July | 1.52 | 1.50 | 1.12 |
| 7 August | 1.5 | 2.02 | 1.69 |
| 22 August | 1.27 | 2.19 | 1.91 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Wang, J.; Liang, S.; Xiao, Z. Extended Data-Based Mechanistic Method for Improving Leaf Area Index Time Series Estimation with Satellite Data. Remote Sens. 2017, 9, 533. https://doi.org/10.3390/rs9060533
Zhou H, Wang J, Liang S, Xiao Z. Extended Data-Based Mechanistic Method for Improving Leaf Area Index Time Series Estimation with Satellite Data. Remote Sensing. 2017; 9(6):533. https://doi.org/10.3390/rs9060533
Chicago/Turabian StyleZhou, Hongmin, Jindi Wang, Shunlin Liang, and Zhiqiang Xiao. 2017. "Extended Data-Based Mechanistic Method for Improving Leaf Area Index Time Series Estimation with Satellite Data" Remote Sensing 9, no. 6: 533. https://doi.org/10.3390/rs9060533
APA StyleZhou, H., Wang, J., Liang, S., & Xiao, Z. (2017). Extended Data-Based Mechanistic Method for Improving Leaf Area Index Time Series Estimation with Satellite Data. Remote Sensing, 9(6), 533. https://doi.org/10.3390/rs9060533