Estimating Time Series Soil Moisture by Applying Recurrent Nonlinear Autoregressive Neural Networks to Passive Microwave Data over the Heihe River Basin, China
Abstract
:1. Introduction
2. Study Area and Data
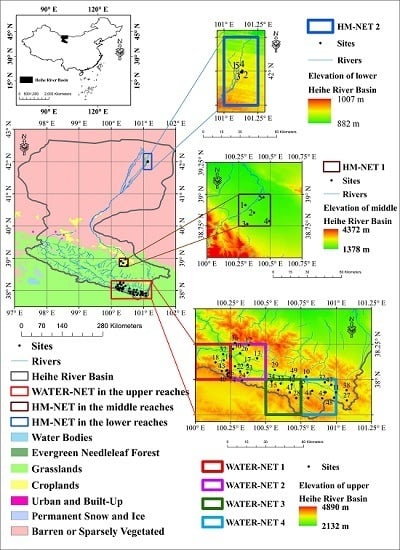
2.1. Study Area
2.2. In Situ Measurements
2.3. Data Sets for NARXnn
2.3.1. The Products of AMSR2
2.3.2. Other Auxiliary Data
2.4. GLDAS
3. Methodology
3.1. NARXnn and its Configuration for SM Retrieval
3.2. Replacement of LST by AMSR2 TB-Ka-V
3.3. Fused SM from JAXA and LPRM
4. Development of the NARXnn
4.1. Preparations before Training
4.2. Training and Testing
4.3. Implement
5. Results and Validation
5.1. Direct Validation
5.2. Indirect Validation
6. Conclusions
- The NARXnn has a seven-dimensional input vector (i.e., TB-X-H, TB-X-V, LAI, TB-Ka-V, PRC, DEM and DOY) and a one-dimensional output vector (SM). Efforts must focus on connecting more correlated variables (e.g., soil texture and land surface roughness) with SM.
- The time series SM predicted by NARXnn was based on a priori information, which likely leads to inaccurate estimation during the freezing/thawing seasons.
- This retrieval method is now being implemented to generate time series SM over the HRB in China from AMSR2 data. It could be applied to other areas and even the globe. In addition, it could also be applied to satellite data from other passive microwave sensors, such as SMAP and SMOS, in the future.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AMSR2 | Advanced Microwave Scanning Radiometer II |
| DEM | Digital elevation model |
| DLNN | Dynamic learning neural network |
| DMS | Defense Meteorological Satellite |
| DOY | Day of year |
| EPLBP | Error propagation learning back propagation |
| GCOM-W1 | Global Change Observation Mission-Water 1 |
| GLASS | Global Land Surface Satellite product |
| GLDAS | Global Land Data Assimilation System |
| GPM | Global Precipitation Measurement |
| GTOPO-30 | Global topography, 30 arc-second spatial resolution |
| HiWATER | Heihe Watershed Allied Telemetry Experimental Research |
| HM-NET | Hydrometeorological observation network |
| HP-II | Hydro Probe II |
| HRB | Heihe River Basin |
| IMERG | Integrated Multi-satellitE Retrievals for GPM |
| JAXA | Japan Aerospace Exploration Agency |
| LAI | Leaf Area Index |
| LPRM | Land surface parameter model |
| LSP/R | Land surface process/radio brightness |
| LSM | Land surface model |
| LST | Land surface temperature |
| MIRAS | Microwave Imaging Radiometer with Aperture Synthesis |
| NARXnn | Nonlinear auto-regressive model with exogenous input neural network |
| NDVI | Normalized Difference Vegetation Index |
| PRC | Precipitation |
| RFI | Radio frequency interference |
| RMSE | Root mean square error |
| SM | Soil moisture |
| SMAP | Soil Moisture Active and Passive |
| SMOS | Soil Moisture and Ocean Salinity |
| SSM/I | Special Sensor Microwave/Imager |
| TB | Brightness temperature |
| TB-X-H | AMSR2 X-band (10.7 GHz) H polarization TB |
| TB-X-V | AMSR2 X-band (10.7 GHz) V polarization TB |
| TB-Ka-V | AMSR2 Ka-band (37 GHz) V polarization TB |
| TDL | Trapped delay line |
| TP | Tibetan Plateau |
| TRMM | Tropical Rainfall Measuring Mission |
| VUA-NASA | Vrije Universiteit Amsterdam and NASA Goddard Space Flight Center |
| WATER-NET | Watershed Allied Telemetry Experimental Research observation network |
References
- Njoku, E.G.; Li, L. Retrieval of land surface parameters using passive microwave measurements at 6–18 GHz. IEEE Trans. Geosci. Remote Sens. 1999, 37, 79–93. [Google Scholar] [CrossRef]
- Fujii, H.; Koike, T.; Imaoka, K. Improvement of the AMSR-E algorithm for soil moisture estimation by introducing a fractional vegetation coverage dataset derived from MODIS data. J. Remote Sens. Soc. Jpn. 2009, 29, 282–292. [Google Scholar]
- Jackson, T.J., III. Measuring Surface Soil Moisture Using Passive Microwave Remote Sensing. Hydrol. Process. 1993, 7, 139–152. [Google Scholar] [CrossRef]
- Jackson, T.J.; Cosh, M.H.; Bindlish, R.; Starks, P.J.; Bosch, D.D.; Seyfried, M.; Goodrich, D.C.; Moran, M.S.; Du, J. Validation of Advanced Microwave Scanning Radiometer Soil Moisture Products. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4256–4272. [Google Scholar] [CrossRef]
- Brocca, L.; Hasenauer, S.; Lacava, T.; Melone, F.; Moramarco, T.; Wagner, W.; Dorigo, W.; Matgen, P.; Martínez-Fernández, J.; Llorens, P.; et al. Soil moisture estimation through ASCAT and AMSR-E sensors: An intercomparison and validation study across Europe. Remote Sens. Environ. 2011, 115, 3390–3408. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, K.; Qin, J.; Zhao, L.; Tang, W.; Han, M. Evaluation of AMSR-E retrievals and GLDAS simulations against observations of a soil moisture network on the central Tibetan Plateau. J. Geophys. Res. Atmos. 2013, 118, 4466–4475. [Google Scholar] [CrossRef]
- Draper, C.S.; Walker, J.P.; Steinle, P.J.; de Jeu, R.A.M.; Holmes, T.R.H. An evaluation of AMSR–E derived soil moisture over Australia. Remote Sens. Environ. 2009, 113, 703–710. [Google Scholar] [CrossRef]
- Liu, Q.; Du, J.; Shi, J.; Jiang, L. Analysis of spatial distribution and multi-year trend of the remotely sensed soil moisture on the Tibetan Plateau. Sci. China Earth Sci. 2013, 56, 2173–2185. [Google Scholar] [CrossRef]
- Yang, J.; Gong, P.; Fu, R.; Zhang, M.; Chen, J.; Liang, S.; Xu, B.; Shi, J.; Dickinson, R. The role of satellite remote sensing in climate change studies. Nat. Clim. Chang. 2013, 3, 875–883. [Google Scholar] [CrossRef]
- Du, J.; Liu, Q. Satellite Detection of Spatial Distribution and Temporal Changes of Surface Soil Moisture at Three Gorges Dam Region from 2003 to 2011. Earth Interact. 2013, 17, 1–13. [Google Scholar] [CrossRef]
- Owe, M.; Van de Griend, A.A.; Jeu, R.; Vries, J.J.; Seyhan, E.; Engman, E.T. Estimating soil moisture from satellite microwave observations: Past and ongoing projects, and relevance to GCIP. J. Geophys. Res. Atmos. 1999, 104, 19735–19742. [Google Scholar] [CrossRef]
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–229. [Google Scholar] [CrossRef]
- Lu, H.; Koike, T.; Fujii, H.; Ohta, T.; Tamagawa, K. Development of a Physically-based Soil Moisture Retrieval Algorithm for Spaceborne Passive Microwave Radiometers and its Application to AMSR-E. J. Remote Sens. Soc. Jpn. 2009, 29, 253–262. [Google Scholar]
- Koike, T.; Nakamura, Y.; Kaihotsu, I.; Davva, G.; Matsuura, N.; Tamagawa, K.; Fujii, H. Development of an advanced microwave scanning radiometer (AMSR-E) algorithm for soil moisture and vegetation water content. Annu. J. Hydraul. Eng. Jpn. Soc. Civ. Eng. 2004, 48, 217–222. [Google Scholar] [CrossRef]
- Owe, M.; de Jeu, R.; Holmes, T. Multisensor historical climatology of satellite - derived global land surface moisture. J. Geophys. Res. Earth Surf. 2008, 113, 196–199. [Google Scholar] [CrossRef]
- Owe, M.; De Jeu, R.; Walker, J. A Methodology for Surface Soil Moisture and Vegetation Optical Depth Retrieval Using the Microwave Polarization Difference Index. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1643–1654. [Google Scholar] [CrossRef]
- Zeng, J.; Li, Z.; Chen, Q.; Bi, H.; Qiu, J.; Zou, P. Evaluation of remotely sensed and reanalysis soil moisture products over the Tibetan Plateau using in-situ observations. Remote Sens. Environ. 2015, 163, 91–110. [Google Scholar] [CrossRef]
- Su, Z.; Wen, J.; Dente, L.; van der Velde, R.; Wang, L.; Ma, Y.; Yang, K.; Hu, Z. The Tibetan Plateau observatory of plateau scale soil moisture and soil temperature (Tibet-Obs) for quantifying uncertainties in coarse resolution satellite and model products. Hydrol. Earth Syst. Sci. 2011, 15, 2303–2316. [Google Scholar] [CrossRef]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating groundwater storage changes in the Mississippi River basin (USA) using GRACE. Hydrogeol. J. 2007, 15, 159–166. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Calvet, J.C.; Pellarin, T.; Van de Griend, A.A.; Berger, M.; Ferrazzoli, P. Retrieving near-surface soil moisture from microwave radiometric observations: Current status and future plans. Remote Sens. Environ. 2003, 85, 489–506. [Google Scholar] [CrossRef]
- Kothari, S.C.; Oh, H. Neural Networks for Pattern Recognition; MIT Press: Cambridge, MA, USA, 1993; pp. 1235–1242. [Google Scholar]
- Nigrin, A. Neural Networks for Pattern Recognition; Oxford university press: Oxford, UK, 2001; pp. 1235–1242. [Google Scholar]
- Abe, S.; Kayama, M.; Takenaga, H.; Kitamura, T. Extracting algorithms from pattern classification neural networks. Neural Netw. 1993, 6, 729–735. [Google Scholar] [CrossRef]
- Li, R.P.; Mukaidono, M.; Turksen, I.B. Study on feature weight and feature selection in pattern classification neural networks. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Beijing, China, 14–17 October 1996; pp. 1972–1976. [Google Scholar]
- Guyon, I. Pattern classification. Pattern Anal. Appl. 1998, 1, 142–143. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1994; pp. 71–80. [Google Scholar]
- Verde, L.; Peiris, H.V.; Spergel, D.N.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; Limon, M. First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Parameter Estimation Methodology. Astrophys. J. Suppl. Ser. 2003, 148, 195. [Google Scholar] [CrossRef]
- Vamsidhar, E.; Varma, K.V.S.R.; Rao, P.S.; Satapati, R. Prediction of Rainfall Using Backpropagation Neural Network Model. Int. J. Comput. Sci. Eng. 2010, 2, 1119–1121. [Google Scholar]
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of general regression neural networks for generating the GLASS leaf area index product from time-series MODIS surface reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Del Frate, F.; Schiavon, G. Nonlinear Principal Component Analysis for the Radiometric Inversion of Atmospheric Profiles by Using Neural Networks. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2335–2342. [Google Scholar] [CrossRef]
- Liou, Y.A.; Tzeng, Y.C.; Chen, K.S. A Neural-Network Approach to Radiometric Sensing of Land-Surface Parameters. IEEE Trans. Geosci. Remote Sens. 1999, 36, 2718–2724. [Google Scholar] [CrossRef]
- Liou, Y.A.; Liu, S.F.; Wang, W.J. Retrieving Soil Moisture from Simulated Brightness Temperatures by a Neural Network. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1662–1672. [Google Scholar]
- Liu, S.; Liou, Y.; Wang, W.; Wigneron, J.; Lee, J. Retrieval of Crop Biomass and Soil Moisture from Measured 1.4 and 10.65 GHz Brightness Temperatures. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1260–1268. [Google Scholar]
- Del Frate, F.; Ferrazzoli, P.; Schiavon, G. Retrieving soil moisture and agricultural variables by microwave radiometry using neural networks. Remote Sens. Environ. 2003, 84, 174–183. [Google Scholar] [CrossRef]
- Chai, S.; Walker, J.P.; Makarynskyy, O.; Kuhn, M.; Veenendaal, B.; West, G. Use of Soil Moisture Variability in Artificial Neural Network Retrieval of Soil Moisture. Remote Sens. 2010, 2, 166–190. [Google Scholar] [CrossRef]
- Santi, E.; Pettinato, S.; Paloscia, S.; Pampaloni, P.; Macelloni, G.; Brogioni, M. An algorithm for generating soil moisture and snow depth maps from microwave spaceborne radiometers: HydroAlgo. Hydrol. Earth Syst. Sci. 2012, 16, 3659–3676. [Google Scholar] [CrossRef]
- Notarnicola, C.; Angiulli, M.; Posa, F. Soil Moisture Retrieval from Remotely Sensed Data: Neural Network Approach Versus Bayesian Method. IEEE Trans. Geosci. Remote Sens. 2008, 46, 547–557. [Google Scholar] [CrossRef]
- Rodriguez-Fernandez, N.J.; Aires, F.; Richaume, P.; Kerr, Y.H.; Prigent, C.; Kolassa, J.; Cabot, F.; Jimenez, C.; Mahmoodi, A.; Drusch, M. Soil Moisture Retrieval Using Neural Networks: Application to SMOS. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5991–6007. [Google Scholar] [CrossRef]
- Cheng, G.; Li, X.; Zhao, W.; Xu, Z.; Feng, Q.; Xiao, S.; Xiao, H. Integrated study of the water–ecosystem–economy in the Heihe River Basin. Nat. Sci. Rev. 2014, 1, 413–428. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y.; et al. Heihe Watershed Allied Telemetry Experimental Research (HiWATER): Scientific Objectives and Experimental Design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Jin, R.; Li, X.; Yan, B.; Li, X.; Ma, M.; Guo, J.; Zhu, Z.; Zhao, S. A Nested Ecohydrological Wireless Sensor Network for Capturing the Surface Heterogeneity in the Midstream Areas of the Heihe River Basin, China. IEEE Trans. Geosci. Remote Sens. 2014, 11, 2015–2019. [Google Scholar] [CrossRef]
- Ge, Y.; Wang, J.H.; Heuvelink, G.B.M.; Jin, R.; Wang, X.L.J.F. Sampling design optimization of a wireless sensor network for monitoring ecohydrological processes in the Babao River basin, China. Int. J. Geogr. Inf. Sci. 2015, 29, 92–110. [Google Scholar] [CrossRef]
- Kang, J.; Li, X.; Jin, R.; Ge, Y.; Wang, J.; Wang, J. Hybrid Optimal Design of the Eco-Hydrological Wireless Sensor Network in the Middle Reach of the Heihe River Basin, China. Sensors 2014, 14, 19095–19114. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Jia, Z.Z.; Zhu, M.J.; Bai, J.; Wang, J.M. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Zhu, Z.L.; Jia, Z.Z.; Zhu, M.J. Measurements of evapotranspiration from eddy-covariance systems and large aperture scintillometers in the Hai River Basin, China. J. Hydrol. 2013, 487, 24–38. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, S.; Li, X.; Shi, S.; Wang, J.; Zhu, Z.; Xu, T.; Wang, W.; Ma, M. Intercomparison of surface energy flux measurement systems used during the HiWATER-MUSOEXE. J. Geophys. Res. Atmos. 2013, 118, 13140–13157. [Google Scholar] [CrossRef]
- Liang, S.; Zhang, X.; Xiao, Z.; Cheng, J.; Liu, Q.; Zhao, X. Global LAnd Surface Satellite (GLASS) Products; Springer International Publishing: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Danielson, J.J.; Jeffrey, J. Delineation of drainage basins from 1 km African digital elevation data. In Proceedings of the Pecora Thirteen, Human Interactions with the Environment-Perspectives from Space, Sioux Falls, SD, USA, 20–22 August 1996. [Google Scholar]
- Gesch, D.B.; Larson, K.S. Techniques for development of global 1-kilometer digital elevation models. In Proceedings of the Pecora Thirteen, Human Interactions with the Environment-Perspectives from Space, Sioux Falls, SD, USA, 20–22 August 1996. [Google Scholar]
- Rodell, M.; Houser, P.R.; Jambor, U.E.A.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M. The global land data assimilation system. Soil Sci. Soc. Am. J. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Kumar, S.; Peterslidard, C.; Tian, Y.; Houser, P.; Geiger, J.; Olden, S.; Lighty, L.; Eastman, J.; Doty, B.; Dirmeyer, P. Land information system: An interoperable framework for high resolution land surface modeling. Environ. Model. Softw. 2006, 21, 1402–1415. [Google Scholar] [CrossRef]
- Siegelmann, H.T.; Horne, B.G.; Giles, C.L. Computational Capabilities of Recurrent NARX Neural Networks. IEEE Trans. Syst. Man Cybern. Soc. Part B Cybern. 1997, 27, 208–215. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.; Horne, B.G.; Tiňo, P.; Giles, L. Learning Long-Term Dependencies in NARX Recurrent Neural Networks. IEEE Trans. Neural Netw. 1996, 7, 1329–1338. [Google Scholar] [PubMed]
- Menezes, J.M.P.; Barreto, G.A. Long-term time series prediction with the NARX network: An empirical evaluation. Neurocomputing 2008, 71, 3335–3343. [Google Scholar] [CrossRef]
- Chai, L.; Qu, Y.; Zhang, L.; Liang, S.; Wang, J. Estimating time-series leaf area index based on recurrent nonlinear autoregressive neural networks with exogenous inputs. Int. J. Remote Sens. 2012, 33, 5712–5731. [Google Scholar] [CrossRef]
- Chen, B.; Wu, Z.; Wang, J.; Dong, J.; Guan, L.; Chen, J.; Yang, K.; Xie, G. Spatio-temporal prediction of leaf area index of rubber plantation using HJ-1A/1B CCD images and recurrent neural network. ISPRS J. Photogram. Remote Sens. 2015, 102, 148–160. [Google Scholar] [CrossRef]
- MacKay, D.J. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Vogl, T.P.; Mangis, J.K.; Rigler, A.K.; Zink, W.T.; Alkon, D.L. Accelerating the convergence of the back-propagation method. Biol. Cybern. 1988, 59, 257–263. [Google Scholar] [CrossRef]
- Owe, M.; Van De Griend, A.A. On the relationship between thermodynamic surface temperature and high-frequency (37 GHz) vertically polarized brightness temperature under semi-arid conditions. Int. J. Remote Sens. 2001, 22, 3521–3532. [Google Scholar] [CrossRef]
- De Jue, R.A.M. Retrieval of Land Surface Parameters Using Passive Microwave Remote Sensing. Ph.D Thesis, Vrije Universiteit Amsterdam, Amsterdam, The Netherland, 2003. [Google Scholar]
- Holmes, T.R.H.; De Jeu, R.A.M.; Owe, M.; Dolman, A.J. Land surface temperature from Ka band (37 GHz) passive microwave observations. J. Geophys. Res. 2009, 114, 83–84. [Google Scholar] [CrossRef]











| RMSE (m3/m3) | R | Beginning (DOY) | End (DOY) | ||||
|---|---|---|---|---|---|---|---|
| Frozen seasons | 0.55795 | 0 1 | 0.04743 | 0.019 | 0.49 | 319 | 84 |
| Unfrozen seasons | 0.38058 | 0.35237 | 0.14116 | 0.067 | 0.76 | 104 | 298 |
| Training Data | Test Data | |
|---|---|---|
| Fused SM Max (m3/m3) | 0.5152 | 0.4618 |
| Corresponding NARXnn SM Max (m3/m3) | 0.5095 | 0.4653 |
| Fused SM Min (m3/m3) | 0.0340 | 0.0360 |
| Corresponding NARXnn SM Min (m3/m3) | 0.0383 | 0.0383 |
| Fused SM Mean (m3/m3) | 0.1731 | 0.1733 |
| Corresponding NARXnn SM Mean (m3/m3) | 0.1730 | 0.1729 |
| RMSE (m3/m3) | 0.0098 | 0.0099 |
| R | 0.9934 | 0.9936 |
| Product | RMSE (m3/m3) | R | Bias | No. 1 | ||
|---|---|---|---|---|---|---|
| The whole year | WATER-NET 1–4 (mean) | NARXnn | 0.060 | 0.90 | −0.02 | 365 |
| JAXA | 0.153 | 0.62 | −0.19 | 281.25 | ||
| LPRM | 0.221 | 0.44 | 0.12 | 243 | ||
| GLDAS | 0.100 | 0.36 | −0.01 | 365 | ||
| HM-NET 1 | NARXnn | 0.043 | 0.85 | 0.01 | 365 | |
| JAXA | 0.076 | 0.35 | −0.06 | 284 | ||
| LPRM | 0.110 | −0.50 | 0.06 | 276 | ||
| GLDAS | 0.063 | 0.34 | 0.04 | 365 | ||
| HM-NET 2 | NARXnn | 0.034 | 0.87 | 0 | 365 | |
| JAXA | 0.091 | 0.40 | −0.03 | 307 | ||
| LPRM | 0.104 | −0.73 | −0.07 | 308 | ||
| GLDAS | 0.074 | 0.13 | −0.02 | 365 | ||
| From May to September | WATER-NET 1–4 (mean) | NARXnn | 0.063 | 0.50 | 0.02 | 153 |
| JAXA | 0.206 | 0.24 | −0.20 | 115.5 | ||
| LPRM | 0.187 | 0.09 | 0.14 | 116.25 | ||
| GLDAS | 0.086 | 0.37 | −0.07 | 153 | ||
| HM-NET 1 | NARXnn | 0.048 | 0.60 | 0.04 | 153 | |
| JAXA | 0.097 | 0.32 | −0.09 | 114 | ||
| LPRM | 0.056 | 0.23 | −0.01 | 117 | ||
| GLDAS | 0.045 | 0.35 | 0.02 | 153 | ||
| HM-NET 2 | NARXnn | 0.032 | 0.58 | −0.01 | 153 | |
| JAXA | 0.121 | 0.33 | −0.12 | 127 | ||
| LPRM | 0.116 | 0.20 | −0.11 | 126 | ||
| GLDAS | 0.092 | 0.42 | −0.08 | 153 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Chai, L.; Liu, S.; Cui, H.; Zhang, Y.; Jiang, L.; Jin, R.; Xu, Z. Estimating Time Series Soil Moisture by Applying Recurrent Nonlinear Autoregressive Neural Networks to Passive Microwave Data over the Heihe River Basin, China. Remote Sens. 2017, 9, 574. https://doi.org/10.3390/rs9060574
Lu Z, Chai L, Liu S, Cui H, Zhang Y, Jiang L, Jin R, Xu Z. Estimating Time Series Soil Moisture by Applying Recurrent Nonlinear Autoregressive Neural Networks to Passive Microwave Data over the Heihe River Basin, China. Remote Sensing. 2017; 9(6):574. https://doi.org/10.3390/rs9060574
Chicago/Turabian StyleLu, Zheng, Linna Chai, Shaomin Liu, Huizhen Cui, Yanghua Zhang, Lingmei Jiang, Rui Jin, and Ziwei Xu. 2017. "Estimating Time Series Soil Moisture by Applying Recurrent Nonlinear Autoregressive Neural Networks to Passive Microwave Data over the Heihe River Basin, China" Remote Sensing 9, no. 6: 574. https://doi.org/10.3390/rs9060574
APA StyleLu, Z., Chai, L., Liu, S., Cui, H., Zhang, Y., Jiang, L., Jin, R., & Xu, Z. (2017). Estimating Time Series Soil Moisture by Applying Recurrent Nonlinear Autoregressive Neural Networks to Passive Microwave Data over the Heihe River Basin, China. Remote Sensing, 9(6), 574. https://doi.org/10.3390/rs9060574