Bathymetry of the Coral Reefs of Weizhou Island Based on Multispectral Satellite Images
Abstract
:1. Introduction
2. Related Works
3. Materials and Methods
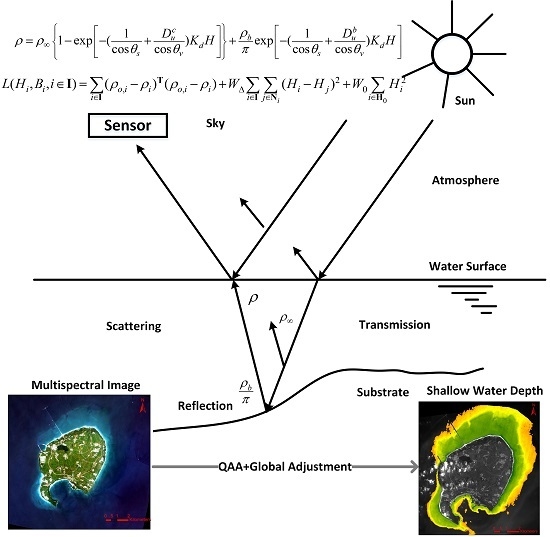
3.1. Overview of the Approach
3.2. Materials and Preprocessing
3.2.1. Experimental Data
3.2.2. Data Preprocessing
3.3. Bathymetric Model and Its Solution
3.3.1. Reduce the Number of Unknowns
3.3.2. Solve the Diffuse Attenuation Coefficient
3.3.3. Initialize the Water Depths
3.4. Global Adjustment of Water Depths
4. Results
4.1. Visualization of the Water Depths
4.2. Evaluations of the Accuracies before and after the Global Adjustment
4.3. Comparisons between the Water Depths Estimated from the Two Different Images
5. Discussion
5.1. Discussion on the Visualization of the Water Depths
5.2. Discussion on the Accuracy Assessment of the Estimated Water Depths
5.3. Discussion on Supplementary Notes and Future Work
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. The Relationship between Backscattering Coefficients and Wavelengths
Appendix B. The Relationship between the Backscattering Coefficient for Particles at 550 nm and the Chlorophyll-a Concentration
References
- Stumpf, P.; Richard, P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Su, H.; Liu, H.; Heyman, W.D. Automated Derivation of Bathymetric Information from Multi-Spectral Satellite Imagery Using a Non-Linear Inversion Model. Mar. Geod. 2008, 31, 281–298. [Google Scholar] [CrossRef]
- Papadopoulou, M.; Lafazani, P.; Mavridou, E.R.; Tsakiri-Strati, M.; Doxani, G. Creation of Digital Bathymetric Maps using High Resolution Satellite Imagery and Multispectral Bathymetric Modeling for Shallow Waters. Tour. Manag. 2015, 14, 407–408. [Google Scholar]
- Brando, V.E.; Anstee, J.M.; Wettle, M.; Dekker, A.G.; Phinn, S.R.; Roelfsema, C. A physics based retrieval and quality assessment of bathymetry from suboptimal hyperspectral data. Remote Sens. Environ. 2009, 113, 755–770. [Google Scholar] [CrossRef]
- Mumby, P.J.; Clark, C.D. Benefits of water column correction and contextual editing for mapping coral reefs. Int. J. Remote Sens. 1998, 19, 203–210. [Google Scholar] [CrossRef]
- Moustier, C.D.; Matsumoto, H. Seafloor acoustic remote sensing with multibeam echo-sounders and bathymetric sidescan sonar systems. Mar. Geophys. Res. 1993, 15, 27–42. [Google Scholar] [CrossRef]
- Chen, E.; Guo, J. Real time map generation using sidescan sonar scanlines for unmanned underwater vehicles. Ocean Eng. 2014, 91, 252–262. [Google Scholar] [CrossRef]
- Montereale-Gavazzi, G.; Roche, M.; Lurton, X.; Degrendele, K.; Terseleer, N.; Lancker, V.V. Seafloor change detection using multibeam echosounder backscatter: Case study on the Belgian part of the North Sea. Mar. Geophys. Res. 2017, 38, 1–19. [Google Scholar] [CrossRef]
- Maleika, W. The influence of track configuration and multibeam echosounder parameters on the accuracy of seabed DTMs obtained in shallow water. Earth Sci. Inform. 2013, 6, 47–69. [Google Scholar] [CrossRef]
- Parnum, I.M.; Gavrilov, A.N. High-frequency multibeam echo-sounder measurements of seafloor backscatter in shallow water: Part 1 Data acquisition and processing. Underw. Technol. Int. J. Soc. Underw. 2011, 30, 3–12. [Google Scholar] [CrossRef]
- Knudby, A.; Ahmad, S.K.; Ilori, C. The Potential for Landsat-based Bathymetry in Canada. Can. J. Remote Sens. 2016, 42, 1–34. [Google Scholar] [CrossRef]
- Wang, W.; Yu, K.; Wang, Y. A Review on the Research of Coral Reefs in the Weizhou Island, Beibu Gulf. Trop. Geogr. 2016, 36, 72–79. [Google Scholar]
- Yu, K. Coral reefs in the South China Sea: Their response to and records on past environmental changes. Sci. China Earth Sci. 2012, 55, 1217–1229. [Google Scholar] [CrossRef]
- Yu, K.; Zhao, J. Coral reefs (of the South China Sea). In The South China Sea—Paleoceanography and Sedimentology, 1st ed.; Wang, P., Li, Q., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 229–248. [Google Scholar]
- Chen, T.; Li, S.; Yu, K.; Zheng, Z.; Wang, L.; Chen, T. Increasing temperature anomalies reduce coral growth in the Weizhou Island, northern South China Sea. Estuar. Coast. Shelf Sci. 2013, 130, 121–126. [Google Scholar] [CrossRef]
- Chen, T.; Zheng, Z.; Mo, S.; Tang, C.; Zhou, X. Bioerosion in Porites corals at Weizhou Island and its environmental significance. Chin. Sci. Bull. 2013, 58, 1574–1582. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef] [PubMed]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral bathymetry using a simple physically based algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Clark, R.K.; Fay, T.H.; Walker, C.L. A Comparison of Models for Remotely Sensed Bathymetry; Naval Ocean Research and Development Activity: Stennis Space Center, MS, USA, 1987. [Google Scholar]
- Doxani, G.; Papadopoulou, M.; Lafazani, P.; Pikridas, C.; Tsakiristrati, M. Shallow-Water Bathymetry over Variable Bottom Types Using Multispectral WORLDVIEW-2 Image. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXIX-B8, 159–164. [Google Scholar] [CrossRef]
- Yuzugullu, O.; Aksoy, A. Generation of the bathymetry of a eutrophic shallow lake using WorldView-2 imagery. J. Hydroinform. 2014, 16, 50–59. [Google Scholar] [CrossRef]
- Mohamed, H.; Negm, A.; Zahran, M.; Saavedra, O.C. Bathymetry Determination from High Resolution Satellite Imagery Using Ensemble Learning Algorithms in Shallow Lakes: Case Study El-Burullus Lake. Int. J. Environ. Sci. Dev. 2016, 7, 295–301. [Google Scholar] [CrossRef]
- Jawak, S.D.; Luis, A.J. High-resolution multispectral satellite imagery for extracting bathymetric information of Antarctic shallow lakes. Proc. SPIE Int. Soc. Opt. Eng. 2016. [Google Scholar] [CrossRef]
- Su, H.; Liu, H.; Wu, Q. Prediction of Water Depth From Multispectral Satellite Imagery—The Regression Kriging Alternative. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2511–2515. [Google Scholar]
- Gholamalifard, M.; Kutser, T.; Esmailisari, A.; Abkar, A.A.; Naimi, B. Remotely Sensed Empirical Modeling of Bathymetry in the Southeastern Caspian Sea. Remote Sens. 2013, 5, 2746–2762. [Google Scholar] [CrossRef]
- Bierwirth, P.N. Shallow sea-floor reflectance and water depth derived by unmixing multispectral imagery. Photogramm. Eng. Remote Sens. 1993, 59, 331–338. [Google Scholar]
- Kutser, T.; Miller, I.; Jupp, D.L.B. Mapping coral reef benthic substrates using hyperspectral space-borne images and spectral libraries. Estuar. Coast. Shelf Sci. 2006, 70, 449–460. [Google Scholar] [CrossRef]
- Lafon, V.; Froidefond, J.M.; Lahet, F.; Castaing, P. SPOT shallow water bathymetry of a moderately turbid tidal inlet based on field measurements. Remote Sens. Environ. 2002, 81, 136–148. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. I. A semianalytical model. Appl. Opt. 1998, 37, 6329–6338. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. 2. Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Carder, K.L.; Chen, R.F.; Peacock, T.G. Properties of the water column and bottom derived from Airborne Visible Infrared Imaging Spectrometer (AVIRIS) data. J. Geophys. Res. 2001, 106, 11639–11652. [Google Scholar] [CrossRef]
- Hedley, J.; Roelfsema, C.; Phinn, S.R. Efficient radiative transfer model inversion for remote sensing applications. Remote Sens. Environ. 2009, 113, 2527–2532. [Google Scholar] [CrossRef]
- Hedley, J.; Russell, B.; Randolph, K.; Dierssen, H. A physics-based method for the remote sensing of seagrasses. Remote Sens. Environ. 2016, 174, 134–147. [Google Scholar] [CrossRef]
- Sylvain, J.; Mireille, G. A novel maximum likelihood based method for mapping depth and water quality from hyperspectral remote-sensing data. Remote Sens. Environ. 2014, 147, 121–132. [Google Scholar]
- Dekker, A.G.; Phinn, S.R.; Anstee, J.; Bissett, P.; Brando, V.E.; Casey, B.; Fearns, P.; Hedley, J.; Klonowski, W.; Lee, Z.P.; et al. Intercomparison of shallow water bathymetry, hydro-optics, and benthos mapping techniques in Australian and Caribbean coastal environments. Limnol. Oceanogr. Methods 2011, 9, 396–425. [Google Scholar] [CrossRef]
- Maritorena, S.; Morel, A.; Gentili, B. Diffuse reflectance of oceanic shallow waters: Influence of water depth and bottom albedo. Limnol. Oceanogr. 1994, 39, 1689–1703. [Google Scholar] [CrossRef]
- Hu, L.; Liu, Z.; Liu, Z.; Hu, C.; He, M.X. Mapping bottom depth and albedo in coastal waters of the South China Sea islands and reefs using Landsat TM and ETM+ data. Int. J. Remote Sens. 2014, 35, 4156–4172. [Google Scholar] [CrossRef]
- Eugenio, F.; Marcello, J.; Martin, J. High-Resolution Maps of Bathymetry and Benthic Habitats in Shallow-Water Environments Using Multispectral Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3539–3549. [Google Scholar] [CrossRef]
- Deren, L.I.; Mi, W. On-orbit Geometric Calibration and Accuracy Assessment of ZY-3. Spacecr. Recover. Remote Sens. 2012, 33, 1–6. [Google Scholar]
- Li, L.; Luo, H.; Zhu, H. Estimation of the Image Interpretability of ZY-3 Sensor Corrected Panchromatic Nadir Data. Remote Sens. 2014, 6, 4409–4429. [Google Scholar] [CrossRef]
- Wen, X.; Shule, G.; Xiaoxiang, L.; Xiaoyan, W.; Junjie, L. Radiometric Image Quality Assessment of ZY-3 TLC Camera. Spacecr. Recover. Remote Sens. 2012, 33, 65–74. [Google Scholar]
- Longbotham, N.W.; Pacifici, F.; Malitz, S.; Baugh, W.; Campsvalls, G. Measuring the Spatial and Spectral Performance of WorldView-3. In Hyperspectral Imaging and Sounding of the Environment 2015; Optical Society of America: Lake Arrowhead, CA, USA, 2015. [Google Scholar]
- Kuester, M.A. Absolute Radiometric Calibration of the DigitalGlobe Fleet and updates on the new WorldView-3 Sensor Suite. In Report of JACIE Civil Commercial Imagery Evaluation Workshop of DigitalGlobe Inc.; DigitalGlobe Inc.: Westminster, CO, USA, 2017; Available online: http://www.digitalglobe.com/resources/technical-information (accessed on 5 May 2017).
- Vermote, E.F.; Tanré, D.; Deuzé, J.L.; Herman, M.; Morcrette, J.J.; Kotchenova, S.Y. Second Simulation of a Satellite Signal in the Solar Spectrum—Vector (6SV). Available online: http://6s.ltdri.org/files/tutorial/6S_Manual_Part_1.pdf (accessed on 20 July 2017).
- Vermote, E.F.; Tanre, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Kotchenova, S.Y.; Vermote, E.F.; Matarrese, R.; Klemm, F.J. Validation of a vector version of the 6S radiative transfer code for atmospheric correction of satellite data. Part I: Path radiance. Appl. Opt. 2006, 45, 6762–6774. [Google Scholar] [CrossRef] [PubMed]
- Tian, Q.; Zheng, L.; Tong, Q. Image based atmospheric radiation correction and reflectance retrieval methods. Q. J. Appl. Meteorl. 1998, 9, 456–461. [Google Scholar]
- Zheng, W.; Zeng, Z.Y. Dark-object methods for atmospheric correction of remote sensing image. Remote Sens. Land Res. 2005, 17, 8–11. [Google Scholar]
- Zhang, B.; Li, J.; Wang, Q.; Shen, X. Hyperspectral Remote Sensing of Inland Water, 1st ed.; Science Press: Beijing, China, 2012. [Google Scholar]
- Li, J.; Zhang, B.; Shen, Q.; Zhang, X.; Chen, Z. Applicaton of Spaceborne Imaging Spectrometry CHRIS in Monitoring of Inland Water Quality. Remote Sens. Technol. Appl. 2007, 22, 593–597. [Google Scholar]
- Tang, J. The Simulation of Marine Optical Properties and Color Sensing Models; The Institute of Remote Sensing Applications (IRSA): Beijing, China; Chinese Academy of Sciences (CAS): Beijing, China, 1999. [Google Scholar]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Tian, G.; Wang, X.; Wang, X.; Song, Q. The Methods of Water Spectra Measurement and Analysis I: Above-Water Method. J. Remote Sens. 2004, 8, 37–44. [Google Scholar]
- Hochberg, E.J.; Andrefouet, S.; Tyler, M.R. Sea surface correction of high spatial resolution Ikonos images to improve bottom mapping in near-shore environments. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1724–1729. [Google Scholar] [CrossRef]
- Eugenio, F.; Martin, J.; Marcello, J.; Fraile-Nuez, E. Environmental monitoring of El Hierro Island submarine volcano, by combining low and high resolution satellite imagery. Int. J. Appl. Earth Obs. Geoinform. 2014, 29, 53–66. [Google Scholar] [CrossRef]
- Prieur, L.; Sathyendranath, S. An Optical Classification of Coastal and Oceanic Waters Based on the Specific Spectral Absorption Curves of Phytoplankton Pigments, Dissolved Organic Matter, and Other Particulate Materials. Limnol. Oceanogr. 1981, 26, 671–689. [Google Scholar] [CrossRef]
- DeBerg, M.; Cheong, O.; van Kreveld, M.; Overmars, M. Computational Geometry: Algorithms and Applications, 2nd ed.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Coleman, T.F.; Li, Y. An Interior Trust Region Approach for Nonlinear Minimization Subject to Bounds. Siam J. Optim. 2006, 6, 418–445. [Google Scholar] [CrossRef]
- Coleman, T.F.; Li, Y. On the convergence of reflective Newton methods for large-scale nonlinear minimization subject to bounds. Math. Progr. 1993, 67, 189–224. [Google Scholar] [CrossRef]
- Liu, J.; Li, G.; Nong, H. Features of geomorphy and Quaternary geology of the Weizhou Island. J. Guangxi Acad. Sci. 1991, 7, 27–35. [Google Scholar]
- Voss, K.J. A spectral model of the beam attenuation coefficient in the ocean and coastal areas. Limnol. Oceanogr. 1992, 37, 501–509. [Google Scholar] [CrossRef]
- Loisel, H.; Morel, A. Light scattering and chlorophyll concentration in case 1 waters: A reexamination. Limnol. Oceanogr. 1998, 43, 847–857. [Google Scholar] [CrossRef]
- Morel, A.E.; Maritorena, S. Bio-optical properties of oceanic waters: A reappraisal. J. Geophys. Res. 2001, 106, 7163–7180. [Google Scholar] [CrossRef]













| Bands | Wavelength (nm) | Radiometric Calibration Coefficients () | |
|---|---|---|---|
| Gain | Offset | ||
| Blue | 450–520 | 0.233 | 0 |
| Green | 520–590 | 0.2162 | 0 |
| Red | 630–690 | 0.1789 | 0 |
| Near-Infrared | 770–890 | 0.1949 | 0 |
| Bands | Coastal | Blue | Green | Yellow | Red | RedEdge |
|---|---|---|---|---|---|---|
| Mean | 0.0482 | 0.0529 | 0.0714 | 0.2776 | 0.4289 | 1.3665 |
| Std. Deviation | 0.00248 | 0.00201 | 0.00112 | 0.00091 | 0.00150 | 0.00073 |
| Skewness | 0.209 | 0.296 | 0.373 | 0.390 | 0.426 | 0.358 |
| Kurtosis 1 | 0.006 | 0.669 | 0.069 | −0.025 | 0.432 | −0.265 |
| Bands | Blue | Green | Red |
|---|---|---|---|
| Mean | 0.0371 | 0.0677 | 0.4143 |
| Std. Deviation | 0.00947 | 0.00329 | 0.00265 |
| Skewness | −0.111 | 0.481 | 0.784 |
| Kurtosis 1 | 0.446 | −0.050 | 0.088 |
| Satellite | Before Global Adjustment | After Global Adjustment | ||||
|---|---|---|---|---|---|---|
| MAX | MAE | RMSE | MAX | MAE | RMSE | |
| ZY-3 | 2.587 | 0.97 | 1.22 | 2.265 | 0.81 | 1.01 |
| WV-3 | 2.11 | 0.58 | 0.75 | 2.27 | 0.56 | 0.77 |
| Author/Method | Location | Data | RMSE (Unit: m) |
|---|---|---|---|
| Hu et al. (2014) | Pratas Atoll | Landsat ETM+ | 1.6 |
| North Danger Reefs | Landsat ETM+ | 1.1 | |
| Eugenio et al. (2015) | Granadilla area of Tenerife Island | WV-2 | 1.20 |
| Corralejo area of Fuerteventura Island | WV-2 | 1.94 | |
| Our Approach | Weizhou Island | ZY-3 | 1.01 |
| Weizhou Island | WV-3 | 0.77 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, R.; Yu, K.; Wang, Y.; Wang, J.; Mu, L.; Wang, W. Bathymetry of the Coral Reefs of Weizhou Island Based on Multispectral Satellite Images. Remote Sens. 2017, 9, 750. https://doi.org/10.3390/rs9070750
Huang R, Yu K, Wang Y, Wang J, Mu L, Wang W. Bathymetry of the Coral Reefs of Weizhou Island Based on Multispectral Satellite Images. Remote Sensing. 2017; 9(7):750. https://doi.org/10.3390/rs9070750
Chicago/Turabian StyleHuang, Rongyong, Kefu Yu, Yinghui Wang, Jikun Wang, Lin Mu, and Wenhuan Wang. 2017. "Bathymetry of the Coral Reefs of Weizhou Island Based on Multispectral Satellite Images" Remote Sensing 9, no. 7: 750. https://doi.org/10.3390/rs9070750
APA StyleHuang, R., Yu, K., Wang, Y., Wang, J., Mu, L., & Wang, W. (2017). Bathymetry of the Coral Reefs of Weizhou Island Based on Multispectral Satellite Images. Remote Sensing, 9(7), 750. https://doi.org/10.3390/rs9070750