1. Introduction
Sources of errors in model estimations are generally of two kinds, input data errors (including initialization) and model errors. One method to decrease deviations of the estimated model states from observations is to optimally “assimilate” observed data of relevant model variables into the model. Data assimilation has a long history as a modeling tool, and in the present article, we will focus on applications to hydrology, with emphasis on soil moisture and streamflow.
Soil moisture is a variable that plays an important role in a hydrological system by regulating several water exchanges and energy fluxes. There are many monitoring networks for soil moisture around the world [
1,
2]. The data from in situ SSM measurements are invaluable in calibrating land surface and hydrological models, while long-term time series can reveal trends due to climate or land use changes. However, in situ soil moisture measurements still remain very sparse, especially compared to the high spatial variability of this variable.
Satellite observations can ensure today complete coverage of large areas and provide a representation of the soil state at regular time intervals. Specifically, as an alternative to ground-based measurements, great efforts have been made in the past two decades to develop soil moisture products from microwave signals with the launch of several instruments on board satellite missions [
3,
4,
5,
6,
7,
8]. Examples of such satellite sensors are the Special Sensor Microwave Imager (SSM/I) on board a series of Defense Meteorological Satellite Program platforms, the Tropical Rainfall Measuring Mission (TRMM) Microwave Imager (TMI) by NASA, the Advanced Microwave Scanning Radiometer-Earth Observing System (AMSR-E) by NASA, its successor AMSR2, the Soil Moisture and Ocean Salinity (SMOS) by ESA, the Soil Moisture Active Passive (SMAP) by NASA and the ASCAT sensor by EUMETSAT. In particular, in [
8], a Land Parameter Retrieval Model (LPRM) is used for surface soil moisture retrievals in order to generate long global series of data. A special algorithm for hydrological applications (HydroAlgo) has been developed in [
9] and used to generate maps of snow depth and soil moisture content from AMSR-E and AMSR2 data.
Each satellite mission carrying such instruments has been designed to satisfy certain technical requirements, e.g., regarding spatial coverage, resolution and scanning frequency. Therefore, significant differences can be expected between the technical specifications of satellite data and the corresponding requirements of several applications in Earth systems, e.g., modeling of the atmosphere and of the hydrological cycle. In fact, many studies have investigated the potential to improve river discharge estimations by using satellite data in hydrological models. This is a complex task, and the outcome depends on the model used, the spatiotemporal scales, the method of using the data (direct use or assimilation) and the quality and availability of the satellite data. For example, [
10] obtain improvements in flood forecasting by complementing discharge data assimilation with soil moisture data assimilation.
Several other studies exist investigating potential benefits of assimilating soil moisture data, e.g., [
11,
12,
13,
14,
15], with encouraging or mixed results. In particular, in [
13], the authors conclude that the underestimation of the vertical soil coupling in the SWAT model impedes the ability of data assimilation to update deep soil moisture. On the other hand, in [
16], soil moisture products have been successfully used in a simplified continuous rainfall-runoff model in order to provide initial wetness conditions prior to a flood event, demonstrating that these products contain useful information, which can be exploited in flood forecasting. Such studies highlight the issues that may arise due to model structure, catchment characteristics and observation errors.
Another frequently-encountered problem is the difference, or bias, in the mean value and variability between different sources of SSM data (satellite retrievals and model integrations in our context). This bias can pose significant obstacles to the use of the information contained in satellite measurements for any kind of application, including data assimilation, and has to be removed. Different methods to remove such bias have been explored in the literature, in particular linear regression, mean and variance matching and Cumulative Distribution Function (CDF) matching [
14,
17,
18,
19,
20,
21]. In [
21], the authors show that proper pre-processing of soil moisture observations can be critical for the performance of the data assimilation.
Estimating an appropriate error for soil moisture observations, used in data assimilation, is still an open problem. One choice is to compare the satellite data with ground-based observations (validation) [
22]. Independent estimations of the error are also possible, e.g., based on triple collocation [
23] and Fourier transforms [
24]. The main difficulties are the higher uncertainty and coarser spatial resolution of the satellite observations, compared to ground-based measurements, and the errors associated with the retrieval algorithms. For an extensive discussion of such issues arising in SSM data assimilation into a hydrological model, we refer the reader to [
25] and the references therein.
The ensemble Kalman filter is a data assimilation method used in geosciences [
26,
27] and in hydrology in particular [
28]. It is a generalization of the common Kalman filter [
29], appropriate for non-linear systems without the need to calculate the adjoint model. However, it was eventually acknowledged that the use of the stochastic terms required by this method may lead to biased estimations if the model includes non-linear processes [
28,
30]. This problem has been considered in other studies too, and a solution has been proposed in [
11,
31]. This solution can be used in cases where the assimilated variable is unconstrained, which is not the case for soil moisture. This is why the approach of [
31] required repeated application of the method in order to further reduce the residual bias due to the bounds of soil moisture. A different problem, but still related to bias, is tackled in [
32], where the EnKF is used in order to find an optimal method to reduce model biases.
The existence of bounds for the assimilated variable gives rise to another problem as well. In the ensemble Kalman filter, the generation and use (as perturbations) of stochastic terms from a normal distribution are generally required. Obviously, repeated application of such perturbations on a bounded variable, like soil moisture, will often drive out of their bounds the values that are already near them. This is another source of biases in the estimations, especially in the most extreme cases (very dry or very wet conditions, speaking of soil moisture). A technique based on variable standard deviation was introduced in [
33] to solve this problem. Although this method reduces the bias due to exceedance of the bounds, it does not completely eliminate it.
In the present study, our goal is to assimilate satellite data for surface soil moisture in the SCHEME hydrological model and to assess the effects of this assimilation in terms of streamflow. The satellite data for soil moisture that we use here are derived from active microwave measurements with the ASCAT sensor on board the MetOp [
7]. The derivation of soil moisture values from such measurements relies on a change detection method [
34]. ASCAT data have been already validated using in situ measurements in southwestern France [
35] yielding encouraging results; see also [
36,
37]. More extensive validation of such data makes up part of the ongoing EUMETSAT project H-SAF. We focus here on the case of a catchment in Belgium while our methodology aims to address the two problems in EnKF pointed out previously.
In our approach, surface soil moisture is properly treated as a bounded variable. In particular, the perturbations needed for the ensemble Kalman filter are generated from truncated normal distributions. This ensures that no soil moisture value exceeds the bounds after the application of perturbations. We use truncated distributions in order to generate perturbations for the precipitation, as well, which is thought of as the forcing of the hydrological model. In this case, the perturbations are applied multiplicatively; therefore, truncated log-normal distributions are used. Of course, precipitation is not bounded in theory from the top, and simple log-normal sampling would suffice. The reason for this unusual, at first sight, choice is that it will ensure that the precipitation values that will be generated by applying such perturbations will remain within the climatological margins.
We tackle in the following way the issue of bias, induced by non-linear processes in conjunction with the use of stochastic terms. Initially, a full data assimilation run is performed. Then, another run is performed in which only perturbations are applied to precipitation, that is the model states are not updated by the Kalman equation. The streamflow ensemble generated by this run is carrying only the bias of the process because there is no assimilated information. The deviation of its mean from the control simulation for the streamflow is then used in order to remove the bias from the full data assimilation ensemble. The introduction and use of truncated probability distributions in a data assimilation scheme and the post-processing technique explained above are the two main advances proposed here.
The article is organized as follows. In
Section 2, we present a description of the hydrological model and the technical details of the assimilation methodology, including the handling of bounded variables and of bias under the presence of non-linear processes. Subsequently, in
Section 3, we deal with the study area and the data used in the numerical experiments. The results are the subject of
Section 4. We conclude by providing more insight in
Section 5.
3. Study Area and Data
Our study is carried out for the catchment of Demer, located in the central-eastern part of Belgium. This catchment covers an area of
and makes part of the Scheldt River Basin (see
Figure 2).
The main land use in the Demer catchment consists of crops (46%), meadows (29%) and forests (18%). The remaining 7% is inhabited. The elevation ranges between 17 and 173 meters, with a mildly hilly profile in the south. The length of the main river is . For the period 1971–2000, the average runoff is about s () and the coldest ones are January s () and daily minimum of s ().
A rain gauge network from the Royal Meteorological Institute of Belgium (approximately one station per ) provides daily rainfall data in the Demer basin. For the period 1966–1995, the average yearly precipitation in the catchment is about . The rainiest month is June, with of rainfall, and the driest one is April with . Therefore, the precipitation is quite uniformly distributed throughout the year, typical for an oceanic climate under some continental influence. The spatial distribution of precipitation is also quite homogeneous due to the almost flat topography of the area.
In the same reference period (1966–1995), the mean temperature is in the Demer catchment. The hottest months are July and August, with and , and the coldest ones are January and February with and respectively.
The study period is 1 June 2013–31 May 2016. The satellite data we use for this period come from the EUMETSAT Satellite Application Facility on Support to Operational Hydrology and Water Management (project H-SAF,
http://hsaf.meteoam.it/). However, older data starting in June 2009 have been used in order to calculate bias correction for soil moisture.
For assimilation purposes, we use the large-scale surface soil moisture product SM-OBS-1(or H07). This product is generated from MetOp scatterometer data (ASCAT) at a coarse resolution (
) controlled by the IFOV of the instrument and provides data for the surface layer of the soil (0.5–2 cm). The measurement of soil moisture with the MetOp scatterometer is fairly direct because of the high sensitivity of the microwaves to the water content of the upper soil layer. This is carried out using the so-called TU-Wien change detection method [
54]. However, the different contributions to the observed total backscatter from the soil, vegetation and soil-vegetation interaction effects cannot be separated. The main assumptions in this approach are linearity in the relation between the backscattering coefficient and surface soil moisture content, stability in time of roughness and land cover and the influence of the vegetation phenology on backscatter at the seasonal time scale only. Snow and frozen soil conditions are not treated in the change detection method, and special care should be taken, using auxiliary information, in order to avoid spurious contributions in winter. In the Demer catchment, forests and topography have a rather limited influence (see
Figure 2 and the catchment metrics in the beginning of this section). Snow presence is also quite limited. The main concern is freezing conditions. We address such issues in the present study by deactivating data assimilation when the mean air temperature falls below 2.0
.
We also use the H-SAF product SM-DAS-2 (or H14) for comparisons with the SCHEME model data at the root zone level. This product is generated in the ECMWF Land Data Assimilation System by assimilating ASCAT SSM data (essentially the H07 product that we discussed previously). In this case, the data assimilation process is based on the extended Kalman filter [
55]. The ECMWF model generates soil moisture profiles according to the Hydrology Tiled ECMWF Scheme for Surface Exchanges over Land (HTESSEL, [
56]) providing estimations for four soil layers for a total thickness of
below the surface. SM-DAS-2 is available at a spatial resolution of
with a daily time step.
Before assimilating the SSM data from H07, a bias correction is applied on them in order to determine the true state in Equation (
6). The H07 data used for this purpose cover the period from June 2009–May 2013, and the reference data are obtained from the output of the SCHEME model. First, the spatial averages over the Demer catchment of all of the necessary data are calculated to produce two four-year-long times series, one from H07 and another one from the model. The bias correction is based on the difference between the distributions represented by the two time series (CDF matching, [
19]). In
Figure 3, we can see the bias as a function of the soil moisture value. Obviously, a piecewise linear interpolation can be used in order to obtain a bias function defined everywhere.
As mentioned in
Section 2, the satellite data are treated in EnKF as random variables (Equation (
6)). This is also useful in the implementation of the data assimilation procedure. In particular, during data assimilation, each pixel of the SCHEME model grid is matched with the closest satellite pixel. This means that about ten SCHEME model pixels are matched with the same satellite pixel. However, the corresponding satellite value is perturbed independently for each model pixel and natural cover inside that pixel, using truncated normal distributions as explained in
Section 2.2.2. This approach yields different perturbed satellite values for each time step, pixel and sub-pixel features of the SCHEME model.
The model error term
in Equation (
5) is calculated as follows in our case. By varying a set of parameters of the SCHEME model, we generate an ensemble of SSM time series with 100 members, as the output of the model runs. Each parameter set defines a variant of the model, which is used in order to produce a long time series of 30 years (1966–1995) for surface soil moisture. In this way, we generate the ensemble of SSM model output. We work with this dataset by dividing first the full SSM range into five classes: 0–20%, 20–40%, 40–60%, 60–80% and 80–100%. These data are then used in order to determine the distribution of the SSM values (
Figure 4) and, for each SSM class, the distribution of the standard deviations (
Figure 5). The former is used in the generation of the initial SSM ensemble at the start day of the assimilation, while the latter in the generation of the error
(Equation (
5)) by sampling a truncated normal distribution.
For the generation of the term
of a given SSM value, we first draw a value from the uniform probability distribution on the interval [0,1]. Using the data represented in
Figure 5, we can then determine the corresponding bin. This bin makes part of the subdivision of the standard deviation interval, which is known and corresponds to the class to which the given SSM value belongs. With this information, we can determine the (randomly drawn) standard deviation
corresponding to the given SSM value. Subsequently we use
in order to define the truncated normal distribution
and randomly draw from it the term
, as described in
Section 2.2.1. The probabilistic context for the generation of the standard deviation
and, subsequently, of the term
described above is new and has not been used in other studies according to our knowledge.
In an analogous way, the perturbations for precipitation (
Section 2.2.2) are generated by sampling a truncated log-normal distribution with the mean equal to one and the standard deviation that depends on the precipitation value. The dependence is determined empirically based on the climatology of the Demer catchment and the ensemble verification measures for streamflow, described in [
30]. In this way, the perturbed precipitation is lying always within the interval
in
. This interval covers all of the cases of daily rainfall in the calibration period of the SCHEME model. The truncated perturbation approach in this context guarantees that no unrealistic precipitation events will be generated during the execution of the data assimilation procedure. Exaggerated precipitation can become a problem with the use of unbounded probability distributions (see
Section 2.2.2), and it has not been previously addressed in the existing literature. The same principle holds for any model sensitive to certain forcing variables.
4. Simulations and Results
The precipitation input and the results of simulations with the SCHEME model are graphically represented in
Figure 6,
Figure 7 and
Figure 8. Each figure corresponds to one of the three years of the study period (June 2013–May 2016). The precipitation and the soil moisture in the two layers of the model are reduced to time series by calculating the areal averages of the corresponding fields over the Demer catchment.
The effect of the assimilation is very obvious at the level of the soil moisture. Regarding the upper layer of the soil, the ensemble generally follows the satellite values. The situation is very different in the lower soil layer, where no assimilation is taking place, but the moisture values are calculated by the SCHEME model after assimilating satellite data at the upper layer. The results of the reference simulation are the only basis for quantitative comparisons that we have for this layer of the soil. In some cases, we observe large deviations between the ensemble members and the reference simulation (e.g., autumn and winter in
Figure 8).
For the streamflow, we have two cases, one ensemble obtained by applying the assimilation procedure (DA) and another one obtained by correcting the previous ensemble for bias (DA-BC), according to the method described in
Section 2.2.3.
In the corresponding figures, the ensemble averages are also depicted together with the control simulation of the model and the streamflow observations. The differences between these time series are quantified using well-established synoptic statistical measures such as bias, Absolute bias (A-bias), root mean square error (RMSE), correlation (R) and Nash–Sutcliffe Efficiency coefficient (NSE). The calculations are carried out at seasonal and annual time scales. The results of such synoptic statistics for all possible combinations of data and time periods are shown in
Table 2,
Table 3 and
Table 4.
Finally, in order to assess the significance of the differences in the scores, we calculate the 95% confidence intervals of the ensemble average scores by using a bootstrap approach. More precisely, each ensemble is randomly sampled in two ways, once in its members and once more in time. We consider the difference between the scores of the control simulation and of the ensemble average as statistically significant if the control value lies outside of the confidence interval.
The qualitative features of the results for the streamflow, seasonal and annual, as well, depend on the period considered. For example, for the year June 2013–May 2014, the average of the DA ensemble yields better annual scores than the reference simulation. The situation is reversed in the year June 2014–May 2015, while in the final period from June 2014–May 2015, the ensemble average becomes again better than the control simulation. However, the differences between the scores are small, and this motivates the use of the statistical significance test mentioned before.
On the other hand, the average of the DA-BC ensemble exhibits more consistent performance in time. For example, its annual scores are all better than the scores of the control simulation in the three years studied here. Like in the case of the DA ensembles, the differences in the scores are small and their significance is checked with the calculation of confidence intervals.
The results of statistical significance analysis using bootstrap replications are presented in
Table 6,
Table 7 and
Table 8. The convention we adopt here is to mark by “Y” differences that are statistically significant and by “N” differences that are not. The “Y” symbol is complemented by the sign + if the corresponding score of the ensemble average is better than the score of the control simulation and by the sign − if it is worse. We use the symbol “Y0” for the only case where the difference is significant, but does not exceed the order of magnitude
in terms of absolute values (
Table 8). We can see for instance that the decrease in the scores for the DA ensemble in June 2014–May 2015 reported previously is indeed significant. Over the same period, the DA-BC ensemble has bias that is consistently lower than the bias of the control simulation, also in a statistically-significant way.
5. Discussion
In this implementation of the ensemble Kalman filter, we can see in a clear way the manifestation of bias due to the use of stochastic perturbations in a nonlinear process. This bias can have unpredictable effects on model performance and can mask the net result of the adjustment applied to the model states through the Kalman equation.
In the three-year period that we study in this article, there are cases of large differences between the control simulation and the ensemble averages for the streamflow during shorter periods of time. For example, from 20 February 2014–6 May 2014, the average of the DA ensemble is a much better approximation of the observations than the control simulation. This is clearly seen in
Table 9 and in
Figure 9. Of particular interest is the very large difference between the NSE coefficients. On the other hand, the average of the DA-BC ensemble is closer to the control simulation in this period with smaller errors, but still a negative NSE coefficient.
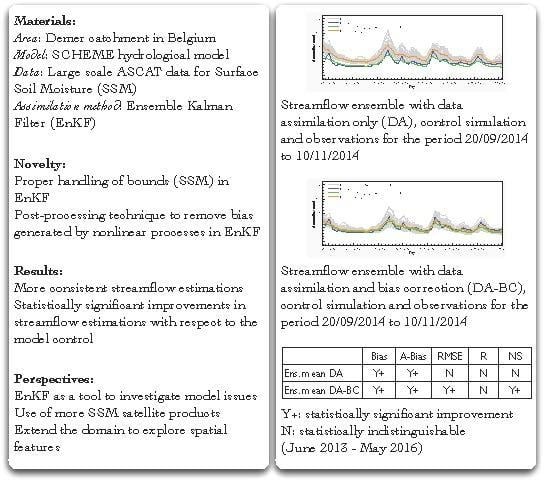
Another typical case is from 20 September 2014–10 November 2014 (
Table 10 and
Figure 10). Over this period, the DA ensemble average yields poor results while the scores of the control simulation appear quite normal, compared to typical SCHEME model performance. Finally, the average of the DA-BC ensemble is slightly better than the control simulation in this case.
The previous situations demonstrate the need to reduce the biases arising in EnKF where non-linear processes take place. The general idea here is to identify the sources of bias and, subsequently, to filter out their effect by running again the model while keeping active the perturbations, which are responsible for bias generation, but without assimilating any data.
It is clear also, at least for this case study, that soil moisture assimilation has a limited impact on the streamflow calculated by the model. This is not surprising because streamflow is mainly determined by precipitation. The assimilation of soil moisture would have more potential in cases where the model does not estimate correctly the water content of the soil, especially in cases with significant amounts of rainfall and saturated soils. Such indications exist also for the SCHEME model in the period that we study here. For example, we see in
Figure 6 that in March 2014, there are large differences between the soil moisture values calculated by the model and detected by the satellite. The net effect of assimilating such satellite data is a slightly better streamflow output from the model (in terms of average of the DA-BC ensemble). This improvement is statistically significant, as is demonstrated in
Table 6.
The moisture variations of the lower soil layer is another point that warrants further investigation. There are systematic differences between the control simulation and the output of the EnKF, which are larger in autumn and the beginning of winter. The origin of such deviations is in part the bias generated by the precipitation perturbations through the nonlinearities of the model and in part the assimilation itself, which transmits the satellite signal from the surface to the lower soil layer through the processes encompassed in the model, with the largest contribution coming from the latter. The lack of any soil moisture measurements for the lower layer prevents at this point a thorough analysis. However, H-SAF provides a root zone soil moisture product, SM-DAS-2 (H14). In order to compare the estimations of H14 and those of the SCHEME model, we can only rescale both in the interval [0,100], because the units are different. Therefore, no proper quantification of the differences could be made in soil moisture units. Nevertheless, visual inspection of the graphs that we provide in
Figure 11 reveals striking similarities between H14 and the ensembles for the lower soil layer, generated by the SCHEME model after assimilating ASCAT SSM data (
Figure 6,
Figure 7 and
Figure 8). This is an example where two completely different modeling approaches (the SCHEME model with EnKF for ASCAT data, on the one hand, and the ECMWF data assimilation system based on extended Kalman filter, on the other) lead to similar conclusions.
6. Conclusions
The purpose of this study is to explore the possibilities to improve streamflow estimation from a hydrological model by assimilating soil moisture data. Our analysis leads to improvements of certain aspects of the ensemble Kalman filter for bounded variables used in nonlinear processes.
The ensemble version of the Kalman filter relies on the repetitive generation of stochastic terms, which are used in order to perturb the ensemble members and calculate state corrections. In the existing literature, this leads systematically to biases, because the perturbations do not in principle preserve the bounds of a variable like the soil moisture. Here, we propose a natural solution to this problem based on truncated probability distributions, which can be applied to the case of any bounded variable.
Another problem is the generation of bias in the model output when such perturbations are applied to a variable that is used in nonlinear processes (soil moisture in our case). The solution proposed here is to identify the source of bias and to isolate its effect by running the model in ensemble mode without assimilating any data, but keeping the perturbations that cause the bias generation. The ensemble obtained in this way can be used to remove the nonlinear processes bias from the full assimilation ensemble.
The combination of the previous steps leads to very consistent data assimilation results. In summary, the streamflow estimations after data assimilation in the SCHEME hydrological model and bias correction are in many cases better than the control simulation of the model in a statistically-significant way. In the remaining situations, these estimations are statistically identical to the control.
Our results point out that the EnKF could be also used as a diagnostic tool to detect weaknesses in a model and to improve its performance. The case of March 2014 reported previously is indicative of such situations. It suggests that further investigation is required regarding the optimization of the SCHEME model parameters that control the seasonal streamflow contribution, especially in spring.
Extending the domain of hydrological simulations into other catchments will provide new insight regarding the spatial features of our data assimilation approach assisted by bias correction. Ultimately, a more extensive use of satellite data could be considered in this context.