Computational Simulations in Advanced Microfluidic Devices: A Review
Abstract
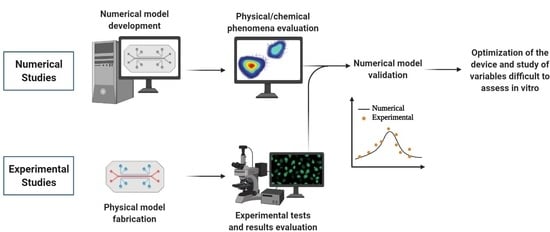
:1. Introduction
2. Applications of Numerical Simulations in Advanced Microfluidic Devices
2.1. Fluid Flow and Mass Transfer
2.2. Nanoparticle Simulations
3. Numerical Optimization
4. Final Remarks and Future Directions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Filipovic, N.; Nikolic, M.; Sustersic, T. Simulation of organ-on-a-chip systems. In Biomaterials for Organ and Tissue Regeneration; Vrana, N.E., Knopf-Marques, H., Barthes, J., Eds.; Woodhead Publishing Series in Biomaterial; Woodhead Publishing: Sawston, UK, 2020. [Google Scholar]
- Soker, S.; Carolina, N. A reductionist metastasis-on-a-chip platform for in vitro tumor progression modeling and drug screening. Biotechnol. Bioeng. 2016, 113, 2020–2032. [Google Scholar] [CrossRef]
- Metiner, P.S.; Gulce-Iz, S.; Biray-Avci, C. Bioengineering-inspired three-dimensional culture systems: Organoids to create tumor microenvironment. Gene 2018, 686, 203–212. [Google Scholar] [CrossRef]
- Banaeiyan, A.A.; Theobald, J.; Paukstyte, J.; Wölfl, S.; Adiels, C.B.; Goksör, M. Design and fabrication of a scalable liver-lobule-on-a-chip microphysiological platform. Biofabrication 2017, 9, 015014. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, V.; Maia, I.; Souza, A.; Ribeiro, J.; Costa, P.; Puga, H.; Teixeira, S.; Lima, R.A. In vitro biomodels in stenotic arteries to perform blood analogues flow visualizations and measurements: A review. Open Biomed. Eng. J. 2020, 14, 87–102. [Google Scholar] [CrossRef]
- Rodrigues, R.O.; Lima, R.; Gomes, H.T.; Silva, A.M.T. Polymer microfluidic devices: An overview of fabrication methods. U. Porto. J. Eng. 2017, 1, 67–79. [Google Scholar] [CrossRef] [Green Version]
- Manz, A.; Graber, N.; Widmer, H. Miniaturized total chemical analysis systems: A novel concept for chemical sensing. Sens. Actuators B Chem. 1990, 1, 244–248. [Google Scholar] [CrossRef]
- Huh, D.; Kim, H.J.; Fraser, J.P.; E Shea, D.; Khan, M.; Bahinski, A.; Hamilton, G.A.; Ingber, D.E. Microfabrication of human organs-on-chips. Nat. Protoc. 2013, 8, 2135–2157. [Google Scholar] [CrossRef]
- Fabre, K.M.; Livingston, C.; Tagle, D.A. Organs-on-chips (microphysiological systems): Tools to expedite efficacy and toxicity testing in human tissue. Exp. Biol. Med. 2014, 239, 1073–1077. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, J.; Wang, X.; Feng, L.; Wu, J.; Zhu, X.; Wen, W.; Gong, X. Organ-on-a-chip: Recent breakthroughs and future prospects. Biomed. Eng. Online 2020, 19, 9. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, V.; Gonçalves, I.; Lage, T.; Rodrigues, R.; Minas, G.; Teixeira, S.; Moita, A.; Hori, T.; Kaji, H.; Lima, R. 3D printing techniques and their applications to organ-on-a-chip platforms: A systematic review. Sensors 2021, 21, 3304. [Google Scholar] [CrossRef]
- Huh, D.; Hamilton, G.A.; Ingber, D.E. From 3D cell culture to organs-on-chips. Trends Cell Biol. 2011, 21, 745–754. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Polini, A.; Prodanov, L.; Bhise, N.S.; Manoharan, V.; Dokmeci, M.R.; Khademhosseini, A. Organs-on-a-chip: A new tool for drug discovery. Expert Opin. Drug Discov. 2014, 9, 335–352. [Google Scholar] [CrossRef] [PubMed]
- Pinho, D.; Carvalho, V.; Gonçalves, I.M.; Teixeira, S.; Lima, R. Visualization and measurements of blood cells flowing in microfluidic systems and blood rheology: A personalized medicine perspective. J. Pers. Med. 2020, 10, 249. [Google Scholar] [CrossRef] [PubMed]
- Faustino, V.; Rodrigues, R.O.; Pinho, D.; Costa, E.; Santos-Silva, A.; Miranda, V.; Amaral, J.S.; Lima, R. A microfluidic deformability assessment of pathological red blood cells flowing in a hyperbolic converging microchannel. Micromachines 2019, 10, 645. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Catarino, S.O.; Rodrigues, R.O.; Pinho, D.; Miranda, J.M.; Minas, G.; Lima, R. Blood cells separation and sorting techniques of passive microfluidic devices: From fabrication to applications. Micromachines 2019, 10, 593. [Google Scholar] [CrossRef] [Green Version]
- Quirós-Solano, W.F.; Gaio, N.; Stassen, O.M.J.A.; Arik, Y.B.; Silvestri, C.; Van Engeland, N.C.A.; van der Meer, A.; Passier, R.; Sahlgren, C.; Bouten, C.; et al. Microfabricated tuneable and transferable porous PDMS membranes for organs-on-chips. Sci. Rep. 2018, 8, 13524. [Google Scholar] [CrossRef]
- Boas, L.V.; Faustino, V.; Lima, R.; Miranda, J.M.; Minas, G.; Fernandes, C.S.V.; Catarino, S.O. Assessment of the deformability and velocity of healthy and artificially impaired red blood cells in narrow polydimethylsiloxane (PDMS) microchannels. Micromachines 2018, 9, 384. [Google Scholar] [CrossRef] [Green Version]
- Lima, R.; Wada, S.; Tanaka, S.; Takeda, M.; Ishikawa, T.; Tsubota, K.-I.; Imai, Y.; Yamaguchi, T. In vitro blood flow in a rectangular PDMS microchannel: Experimental observations using a confocal micro-PIV system. Biomed. Microdevices 2008, 10, 153–167. [Google Scholar] [CrossRef] [Green Version]
- Pinho, D.; Muñoz-Sánchez, B.N.; Anes, C.F.; Vega, E.J.; Lima, R. Flexible PDMS microparticles to mimic RBCs in blood particulate analogue fluids. Mech. Res. Commun. 2019, 100, 103399. [Google Scholar] [CrossRef] [Green Version]
- Mata, A.; Fleischman, A.J.; Roy, S. Characterization of polydimethylsiloxane (PDMS) properties for biomedical micro/nanosystems. Biomed. Microdevices 2005, 7, 281–293. [Google Scholar] [CrossRef]
- Leclerc, E.; Sakai, Y.; Fujii, T. Cell culture in 3-dimensional microfluidic structure of PDMS (polydimethylsiloxane). Biomed. Microdevices 2003, 5, 109–114. [Google Scholar] [CrossRef]
- Halldorsson, S.; Lucumi, E.; Gomez-Sjoberg, R.; Fleming, R.M. Advantages and challenges of microfluidic cell culture in polydimethylsiloxane devices. Biosens. Bioelectron. 2015, 63, 218–231. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Chen, S.; Sun, H.; Li, W.; Hu, C.; Ren, K. Recent progresses in microfabricating perfluorinated polymers (Teflons) and the associated new applications in microfluidics. Microphysiol. Syst. 2018, 2, 6. [Google Scholar] [CrossRef]
- Sosa-Hernández, J.E.; Villalba-Rodríguez, A.M.; Romero-Castillo, K.D.; Aguilar-Aguila-Isaías, M.A.; García-Reyes, I.E.; Hernández-Antonio, A.; Ahmed, I.; Sharma, A.; Parra-Saldívar, R.; Iqbal, H.M.N. Organs-on-a-chip module: A review from the development and applications perspective. Micromachines 2018, 9, 536. [Google Scholar] [CrossRef] [Green Version]
- Sakamiya, M.; Fang, Y.; Mo, X.; Shen, J.; Zhang, T. A heart-on-a-chip platform for online monitoring of contractile behavior via digital image processing and piezoelectric sensing technique. Med. Eng. Phys. 2019, 75, 36–44. [Google Scholar] [CrossRef]
- Zamprogno, P.; Wüthrich, S.; Achenbach, S.; Thoma, G.; Stucki, J.D.; Hobi, N.; Schneider-Daum, N.; Lehr, C.-M.; Huwer, H.; Geiser, T.; et al. Second-generation lung-on-a-chip with an array of stretchable alveoli made with a biological membrane. Commun. Biol. 2021, 4, 168. [Google Scholar] [CrossRef]
- Deng, J.; Wei, W.; Chen, Z.; Lin, B.; Zhao, W.; Luo, Y.; Zhang, X. Engineered liver-on-a-chip platform to mimic liver functions and its biomedical applications: A review. Micromachines 2019, 10, 676. [Google Scholar] [CrossRef] [Green Version]
- Benam, K.H.; Dauth, S.; Hassell, B.; Herland, A.; Jain, A.; Jang, K.-J.; Karalis, K.; Kim, H.J.; MacQueen, L.; Mahmoodian, R.; et al. Engineered in vitro disease models. Annu. Rev. Pathol. Mech. Dis. 2015, 10, 195–262. [Google Scholar] [CrossRef] [Green Version]
- Ndyabawe, K.; Cipriano, M.; Zhao, W.; Haidekker, M.; Yao, K.; Mao, L.; Kisaalita, W.S. Brain-on-a-chip device for modeling multiregional networks. ACS Biomater. Sci. Eng. 2021, 7, 350–359. [Google Scholar] [CrossRef]
- Hao, S.; Ha, L.; Cheng, G.; Wan, Y.; Xia, Y.; Sosnoski, D.M.; Mastro, A.M.; Zheng, S.-Y. A spontaneous 3D bone-on-a-chip for bone metastasis study of breast cancer cells. Small 2018, 14, e1702787. [Google Scholar] [CrossRef]
- Sung, J.H.; Wang, Y.I.; Sriram, N.N.; Jackson, M.; Long, C.; Hickman, J.J.; Shuler, M.L. Recent advances in body-on-a-chip systems. Anal. Chem. 2019, 91, 330–351. [Google Scholar] [CrossRef] [PubMed]
- Shuler, M.L. Organ-, body- and disease-on-a-chip systems. Lab Chip 2017, 17, 2345–2346. [Google Scholar] [CrossRef] [PubMed]
- Si, L.; Bai, H.; Rodas, M.; Cao, W.; Oh, C.Y.; Jiang, A.; Moller, R.; Hoagland, D.; Oishi, K.; Horiuchi, S.; et al. A human-airway-on-a-chip for the rapid identification of candidate antiviral therapeutics and prophylactics. Nat. Biomed. Eng. 2021, 5, 815–829. [Google Scholar] [CrossRef]
- Sung, J.H.; Wang, Y.; Shuler, M.L. Strategies for using mathematical modeling approaches to design and interpret multi-organ microphysiological systems (MPS). APL Bioeng. 2019, 3, 021501. [Google Scholar] [CrossRef]
- Wong, J.F.; Young, E.W.K.; Simmons, C.A. Computational analysis of integrated biosensing and shear flow in a microfluidic vascular model. AIP Adv. 2017, 7, 115116. [Google Scholar] [CrossRef] [Green Version]
- Sheidaei, Z.; Akbarzadeh, P.; Kashaninejad, N. Advances in numerical approaches for microfluidic cell analysis platforms. J. Sci. Adv. Mater. Devices 2020, 5, 295–307. [Google Scholar] [CrossRef]
- Carvalho, V.; Pinho, D.; Lima, R.A.; Teixeira, J.C.; Teixeira, S. Blood flow modeling in coronary arteries: A review. Fluids 2021, 6, 53. [Google Scholar] [CrossRef]
- Lopes, D.; Agujetas, R.; Puga, H.; Teixeira, J.; Lima, R.; Alejo, J.; Ferrera, C. Analysis of finite element and finite volume methods for fluid-structure interaction simulation of blood flow in a real stenosed artery. Int. J. Mech. Sci. 2021, 207, 106650. [Google Scholar] [CrossRef]
- Carvalho, V.; Rodrigues, N.; Ribeiro, R.; Costa, P.F.; Teixeira, J.C.F.; Lima, R.A.; Teixeira, S.F.C.F. Hemodynamic study in 3D printed stenotic coronary artery models: Experimental validation and transient simulation. Comput. Methods Biomech. Biomed. Eng. 2020, 24, 623–636. [Google Scholar] [CrossRef]
- Carvalho, V.; Rodrigues, N.; Ribeiro, R.; Costa, P.F.; Lima, R.A.; Teixeira, S.F. 3D printed biomodels for flow visualization in stenotic vessels: An experimental and numerical study. Micromachines 2020, 11, 549. [Google Scholar] [CrossRef]
- Doutel, E.; Viriato, N.; Carneiro, J.; Campos, J.B.; Miranda, J.M. Geometrical effects in the hemodynamics of stenotic and non-stenotic left coronary arteries—Numerical and in vitro approaches. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3207. [Google Scholar] [CrossRef]
- Rodrigues, R.O.; Sousa, P.C.; Gaspar, J.; Bañobre-López, M.; Lima, R.; Minas, G. Organ-on-a-chip: A preclinical microfluidic platform for the progress of nanomedicine. Small 2020, 16, e2003517. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Wereley, S.T.; Shaegh, S.A.M. Fundamentals and Applications of Microfluidics, 3rd ed.; Artech House: Norwood, MA, USA, 2019; Volume 110. [Google Scholar]
- Kocal, G.C.; Guven, S.; Foygel, K.; Goldman, A.; Chen, P.; Sengupta, S.; Paulmurugan, R.; Baskin, Y.; Demirci, U. Dynamic microenvironment induces phenotypic plasticity of esophageal cancer cells under flow. Sci. Rep. 2016, 6, 38221. [Google Scholar] [CrossRef] [Green Version]
- Lo, K.-Y.; Zhu, Y.; Tsai, H.-F.; Sun, Y.-S. Effects of shear stresses and antioxidant concentrations on the production of reactive oxygen species in lung cancer cells. Biomicrofluidics 2013, 7, 64108. [Google Scholar] [CrossRef] [Green Version]
- Kou, S.; Pan, L.; van Noort, D.; Meng, G.; Wu, X.; Sun, H.; Xu, J.; Lee, I. A multishear microfluidic device for quantitative analysis of calcium dynamics in osteoblasts. Biochem. Biophys. Res. Commun. 2011, 408, 350–355. [Google Scholar] [CrossRef]
- Komen, J.; Westerbeek, E.Y.; Kolkman, R.W.; Roesthuis, J.; Lievens, C.; Berg, A.V.D.; Van Der Meer, A.D. Controlled pharmacokinetic anti-cancer drug concentration profiles lead to growth inhibition of colorectal cancer cells in a microfluidic device. Lab Chip 2020, 20, 3167–3178. [Google Scholar] [CrossRef]
- Wong, J.F.; Simmons, C.A. Microfluidic assay for the on-chip electrochemical measurement of cell monolayer permeability. Lab Chip 2019, 19, 1060–1070. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Xue, J.; Hu, J.; Ding, Q.; Zhou, L.; Feng, S.; Cui, Y.; Lü, S.; Long, M. Flow field analyses of a porous membrane-separated, double-layered microfluidic chip for cell co-culture. Acta Mech. Sin. 2020, 36, 754–767. [Google Scholar] [CrossRef]
- Mosavati, B.; Oleinikov, A.V.; Du, E. Development of an organ-on-a-chip-device for study of placental pathologies. Int. J. Mol. Sci. 2020, 21, 8755. [Google Scholar] [CrossRef]
- Hu, G.; Li, D. Three-dimensional modeling of transport of nutrients for multicellular tumor spheroid culture in a microchannel. Biomed. Microdevices 2007, 9, 315–323. [Google Scholar] [CrossRef] [PubMed]
- Zahorodny-Burke, M.; Nearingburg, B.; Elias, A. Finite element analysis of oxygen transport in microfluidic cell culture devices with varying channel architectures, perfusion rates, and materials. Chem. Eng. Sci. 2011, 66, 6244–6253. [Google Scholar] [CrossRef]
- Bhise, N.S.; Manoharan, V.; Massa, S.; Tamayol, A.; Ghaderi, M.; Miscuglio, M.; Lang, Q.; Zhang, Y.S.; Shin, S.R.; Calzone, G.; et al. A liver-on-a-chip platform with bioprinted hepatic spheroids. Biofabrication 2016, 8, 014101. [Google Scholar] [CrossRef] [PubMed]
- Mäki, A.-J.; Peltokangas, M.; Kreutzer, J.; Auvinen, S.; Kallio, P. Modeling carbon dioxide transport in PDMS-based microfluidic cell culture devices. Chem. Eng. Sci. 2015, 137, 515–524. [Google Scholar] [CrossRef]
- Cicchetti, A.; Laurino, F.; Possenti, L.; Rancati, T.; Zunino, P. In silico model of the early effects of radiation therapy on the microcirculation and the surrounding tissues. Phys. Medica 2020, 73, 125–134. [Google Scholar] [CrossRef]
- Kim, M.; Kim, G.; Kim, D.; Yoo, J.; Kim, D.-K.; Kim, H. Numerical study on effective conditions for the induction of apoptotic temperatures for various tumor aspect ratios using a single continuous-wave laser in photothermal therapy using gold nanorods. Cancers 2019, 11, 764. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Fang, C.; Ren, S.; Pan, J.; Jia, Y.; Shu, Z.; Gao, D. Development of a microfluidic device with precise on-chip temperature control by integrated cooling and heating components for single cell-based analysis. Int. J. Heat Mass Transf. 2019, 130, 660–667. [Google Scholar] [CrossRef]
- Das, S.K.; Chung, S.; Zervantonakis, I.; Atnafu, J.; Kamm, R.D. A microfluidic platform for studying the effects of small temperature gradients in an incubator environment. Biomicrofluidics 2008, 2, 034106. [Google Scholar] [CrossRef] [Green Version]
- Hynes, W.F.; Pepona, M.; Robertson, C.; Alvarado, J.; Dubbin, K.; Triplett, M.; Adorno, J.J.; Randles, A.; Moya, M.L. Examining metastatic behavior within 3D bioprinted vasculature for the validation of a 3D computational flow model. Sci. Adv. 2020, 6, eabb3308. [Google Scholar] [CrossRef]
- Ye, T.; Shi, H.; Phan-Thien, N.; Lim, C.T.; Li, Y. Numerical design of a microfluidic chip for probing mechanical properties of cells. J. Biomech. 2019, 84, 103–112. [Google Scholar] [CrossRef]
- Zhang, M.; Zheng, A.; Zheng, Z.C.; Wang, M.Z. Multiphase flow experiment and simulation for cells-on-a-chip devices. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2019, 233, 432–443. [Google Scholar] [CrossRef]
- Tanaka, N.; Yamashita, T.; Yalikun, Y.; Amaya, S.; Sato, A.; Vogel, V.; Tanaka, Y. An ultra-small fluid oscillation unit for pumping driven by self-organized three-dimensional bridging of pulsatile cardiomyocytes on elastic micro-piers. Sens. Actuators B Chem. 2019, 293, 256–264. [Google Scholar] [CrossRef]
- Subramaniam, A.; Sethuraman, S. Biomedical applications of nondegradable polymers. In Natural and Synthetic Biomedical Polymers; Elsevier Science: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Lamberti, A.; Marasso, S.L.; Cocuzza, M. PDMS membranes with tunable gas permeability for microfluidic applications. RSC Adv. 2014, 4, 61415–61419. [Google Scholar] [CrossRef]
- Li, J.M.; Liu, C.; Dai, X.D.; Chen, H.H.; Liang, Y.; Sun, H.L.; Tian, H.; Ding, X.P. PMMA microfluidic devices with three-dimensional features for blood cell filtration. J. Micromechanics Microengineering 2008, 18, 95021. [Google Scholar] [CrossRef]
- Faustino, V.; Catarino, S.O.; Lima, R.; Minas, G. Biomedical microfluidic devices by using low-cost fabrication techniques: A review. J. Biomech. 2016, 49, 2280–2292. [Google Scholar] [CrossRef] [Green Version]
- Singhal, J.; Pinho, D.; Lopes, R.; Sousa, P.C.; Garcia, V.; Schutte, H.; Lima, R.; Gassmann, S. Blood flow visualization and measurements in microfluidic devices fabricated by a micromilling technique. Micro Nanosyst. 2015, 7, 148–153. [Google Scholar] [CrossRef] [Green Version]
- Lopes, R.; Rodrigues, R.O.; Pinho, D.; Garcia, V.; Schütte, H.; Lima, R.; Gassmann, S. Low cost microfluidic device for partial cell separation: Micromilling approach. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 3347–3350. [Google Scholar]
- Aghvami, S.A.; Opathalage, A.; Zhang, Z.; Ludwig, M.; Heymann, M.; Norton, M.; Wilkins, N.; Fraden, S. Rapid prototyping of cyclic olefin copolymer (COC) microfluidic devices. Sens. Actuators B Chem. 2017, 247, 940–949. [Google Scholar] [CrossRef]
- Ochs, C.J.; Kasuya, J.; Pavesi, A.; Kamm, R.D. Oxygen levels in thermoplastic microfluidic devices during cell culture. Lab Chip 2014, 14, 459–462. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Santiago, G.T.-D.; Flores-Garza, B.G.; Negrete, J.T.; Lara-Mayorga, I.M.; González-Gamboa, I.; Zhang, Y.S.; Rojas-Martínez, A.; Ortiz-López, R.; Álvarez, M.M. The tumor-on-chip: Recent advances in the development of microfluidic systems to recapitulate the physiology of solid tumors. Materials 2019, 12, 2945. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hua, S.; De Matos, M.B.C.; Metselaar, J.M.; Storm, G. Current trends and challenges in the clinical translation of nanoparticulate nanomedicines: Pathways for translational development and commercialization. Front. Pharmacol. 2018, 9, 790. [Google Scholar] [CrossRef]
- Ahn, J.; Ko, J.; Lee, S.; Yu, J.; Kim, Y.; Jeon, N.L. Microfluidics in nanoparticle drug delivery; From synthesis to pre-clinical screening. Adv. Drug Deliv. Rev. 2018, 128, 29–53. [Google Scholar] [CrossRef]
- Soheili, S.; Mandegar, E.; Moradikhah, F.; Doosti-Telgerd, M.; Javar, H.A. Experimental and numerical studies on microfluidic preparation and engineering of chitosan nanoparticles. J. Drug Deliv. Sci. Technol. 2020, 61, 102268. [Google Scholar] [CrossRef]
- Arefi, S.M.A.; Yang, C.W.T.; Sin, D.D.; Feng, J.J. Simulation of nanoparticle transport and adsorption in a microfluidic lung-on-a-chip device. Biomicrofluidics 2020, 14, 044117. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Bhattacharya, A.; Kuksenok, O.; He, X.; Aizenberg, M.; Aizenberg, J.; Balazs, A.C. Computational modeling of oscillating fins that “catch and release” targeted nanoparticles in bilayer flows. Soft Matter 2016, 12, 1374–1384. [Google Scholar] [CrossRef] [PubMed]
- Maleki, R.; Khedri, M.; Malekahmadi, D.; Mohaghegh, S.; Jahromi, A.M.; Shahbazi, M.A. Simultaneous doxorubicin encap-sulation and in-situ microfluidic micellization of bio-targeted polymeric nanohybrids using dichalcogenide monolayers: A Molecular in-silico study. Mater. Today Commun. 2021, 26, 101948. [Google Scholar] [CrossRef]
- Kwak, B.; Ozcelikkale, A.; Shin, C.; Park, K.; Han, B. Simulation of complex transport of nanoparticles around a tumor using tumor-microenvironment-on-chip. J. Control. Release 2014, 194, 157–167. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nasiri, R.; Shamloo, A.; Akbari, J.; Tebon, P.; Dokmeci, M.R.; Ahadian, S. Design and simulation of an integrated centrifugal microfluidic device for CTCs separation and cell lysis. Micromachines 2020, 11, 699. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, X.; Ren, Y.; Yan, Y.; Wu, A. Numerical simulation of circulating tumor cell separation in a dielectrophoresis based Y-Y shaped microfluidic device. Sep. Purif. Technol. 2021, 255, 117343. [Google Scholar] [CrossRef]
- Ma, J.-T.; Xu, Y.-Q.; Tang, X.-Y. A numerical simulation of cell separation by simplified asymmetric pinched flow fractionation. Comput. Math. Methods Med. 2016, 2016, 2564584. [Google Scholar] [CrossRef] [Green Version]
- Shamloo, A.; Boodaghi, M. Design and simulation of a microfluidic device for acoustic cell separation. Ultrasonics 2018, 84, 234–243. [Google Scholar] [CrossRef]
- Karakas, H.E.; Kim, J.; Park, J.; Oh, J.M.; Choi, Y.; Gozuacik, D.; Cho, Y.-K. A microfluidic chip for screening individual cancer cells via eavesdropping on autophagy-inducing crosstalk in the stroma niche. Sci. Rep. 2017, 7, 2050. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.-S.; Zhang, Y.-Y.; Wang, Z.; Deng, J.-Y.; Ye, X.; Xue, R.-Y.; Ge, D.; Xu, Z. Design and validation of a microfluidic chip with micropillar arrays for three-dimensional cell culture. Chin. J. Anal. Chem. 2017, 45, 1109–1114. [Google Scholar] [CrossRef]
- Chen, W.; Li, J.; Wan, X.; Zou, X.; Qi, S.; Zhang, Y.; Weng, Q.; Li, J.; Xiong, W.; Xie, C.; et al. Design of a microfluidic chip consisting of micropillars and its use for the enrichment of nasopharyngeal cancer cells. Oncol. Lett. 2019, 17, 1581–1588. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Nguyen, N.-T. A polymeric cell stretching device for real-time imaging with optical microscopy. Biomed. Microdevices 2013, 15, 1043–1054. [Google Scholar] [CrossRef] [PubMed]







| Software | Flow Regime | Phases Number | Fluid Rheology | Mesh | Time- Dependence | Validation | Ref |
|---|---|---|---|---|---|---|---|
| COMSOL | Laminar and turbulent | Single-phase | Newtonian | n/d | Steady | × | [45] |
| CFD-ACE + | Laminar | Single-phase | n/d | n/d | Steady | ✓ | [46] |
| Ansys | Laminar | Single-phase | Newtonian | 78,000 nodes | Steady | × | [47] |
| COMSOL | n/d | Single-phase | n/d | n/d | Transient | ✓ | [48] |
| COMSOL | Laminar | Single-phase | Newtonian | 182,900 elements | Transient | × | [36] |
| n/d | Laminar | Single-phase | n/d | n/d | Transient | ✓ | [49] |
| IBM, MATLAB and Ansys | Laminar | Multiphase | Newtonian | Mesh independence test (1 µm) | Transient | × | [50] |
| COMSOL | Laminar | Single-phase | Newtonian | Mesh independence test (n/d) | Transient | ✓ | [51] |
| COMSOL | Laminar | Single-phase | Newtonian | Fine mesh (n/d) | Transient | × | [4] |
| COMSOL | n/d | Single-phase | n/d | n/d | Transient | ✓ | [52] |
| COMSOL | Laminar | Single-phase | n/d | 7000 elements | Steady | ✓ | [53] |
| COMSOL | n/d | Single-phase | n/d | Mesh independence test (800,000 nodes) | Transient | × | [54] |
| COMSOL | n/d | Multiphase | Newtonian | 24,300 elements | Transient | ✓ | [55] |
| User-Defined Software | Laminar | Single-phase | n/d | n/d | Steady | × | [56] |
| COMSOL | Laminar | Single-phase | n/d | n/d | Steady | × | [58] |
| COMSOL | Laminar | Single-phase | n/d | 123,334 elements | Steady | ✓ | [59] |
| User-Defined Software | n/d | Multiphase | Newtonian | n/d | Transient | ✓ | [60] |
| SDPD and IBM | n/d | Multiphase | n/d | n/d | Transient | ✓ | [61] |
| Ansys | Laminar | Multiphase | Newtonian | Mesh independence test (220,000 elements) | Transient | ✓ | [62] |
| Ansys | Laminar | Multiphase | Newtonian | n/d | Steady | ✓ | [63] |
| COMSOL | n/d | Single-phase | n/d | elements | Transient | ✓ | [71] |
| COMSOL | Laminar | Multiphase | n/d | Mesh independence test (6000 elements) | Transient | × | [75] |
| n/d | n/d | Multiphase | n/d | n/d | Transient | ✓ | [79] |
| n/d | n/d | Multiphase | n/d | n/d | Transient | × | [77] |
| GROMACS | n/d | Multiphase | Newtonian | n/d | Transient | ✓ | [78] |
| COMSOL | Laminar | Multiphase | n/d | Mesh independence test (168,000 elements) | Steady and Transient | ✓ | [76] |
| COMSOL | n/d | Single-phase | n/d | n/d | Transient | × | [84] |
| n/d | n/d | Multiphase | n/d | n/d | Transient | × | [81] |
| COMSOL and Ansys | n/d | Single-phase | n/d | n/d | Transient | ✓ | [85] |
| Ansys | n/d | Single-phase | n/d | n/d | Steady | × | [86] |
| Ansys | n/d | Single-phase | n/d | 2–8 μm element size | Transient | ✓ | [87] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvalho, V.; Rodrigues, R.O.; Lima, R.A.; Teixeira, S. Computational Simulations in Advanced Microfluidic Devices: A Review. Micromachines 2021, 12, 1149. https://doi.org/10.3390/mi12101149
Carvalho V, Rodrigues RO, Lima RA, Teixeira S. Computational Simulations in Advanced Microfluidic Devices: A Review. Micromachines. 2021; 12(10):1149. https://doi.org/10.3390/mi12101149
Chicago/Turabian StyleCarvalho, Violeta, Raquel O. Rodrigues, Rui A. Lima, and Senhorinha Teixeira. 2021. "Computational Simulations in Advanced Microfluidic Devices: A Review" Micromachines 12, no. 10: 1149. https://doi.org/10.3390/mi12101149
APA StyleCarvalho, V., Rodrigues, R. O., Lima, R. A., & Teixeira, S. (2021). Computational Simulations in Advanced Microfluidic Devices: A Review. Micromachines, 12(10), 1149. https://doi.org/10.3390/mi12101149