Modeling of Key Specifications for RF Amplifiers Using the Extreme Learning Machine
Abstract
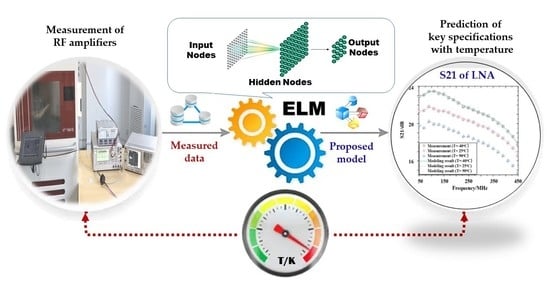
:1. Introduction
2. Designed Circuits and Experiments
3. Modeling Process
3.1. Structure of the Model and the Process of Modeling
- Step 1:
- Step 2:
- Divide the simulation data into training data and test data.
- Step 3:
- Determine the initial number of hidden layer layers (L) and hidden layer output weights (βi) of the model.
- Step 4:
- Randomly generate input weights (ai) and hidden layer weights (bi).
- Step 5:
- Output the model results.
- Step 6:
- Calculate the model error (MSE1).
- Step 7:
- Calibrate of the model using the test results.
- Step 8:
- Compare the model error with the expected value.
- Step 9:
- Determine whether the model is trained or not based on comparing the model error with the expected value.
3.2. ELM Training Algorithm
- (1)
- Randomly assign the hidden node parameters, e.g., the input weights (ai) and hidden layer weights (bi), i = 1, …, L.
- (2)
- Calculate the hidden layer output matrix H.
- (3)
- Obtain the output weight vector.
3.3. Error of the Model
4. Modeling Results and Discussion
4.1. 0.5−2.1 GHz GaN Class AB PA
4.1.1. S21
4.1.2. Output Power
4.2. 50−450 MHz CMOS LNA
4.2.1. S21
4.2.2. The NF of the LNA
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moreno Rubio, J.J.; Angarita Malaver, E.F.; Lara González, L.Á. Wideband Doherty Power Amplifier: A Design Approach. Micromachines 2022, 13, 497. [Google Scholar] [CrossRef]
- Balani, W.; Sarvagya, M.; Ali, T.; Samasgikar, A.; Kumar, P.; Pathan, S.; Pai, M.M.M. A 20–44 GHz Wideband LNA Design Using the SiGe Technology for 5G Millimeter-Wave Applications. Micromachines 2021, 12, 1520. [Google Scholar] [CrossRef] [PubMed]
- Zurek, P.; Cappello, T.; Popovic, Z. Broadband Diplexed Power Amplifier. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 1073–1076. [Google Scholar] [CrossRef]
- Jing, X.; Zhong, S.; Wang, H.; You, F. A 150 W Space-Borne GaN Solid State Power Amplifier for BeiDou Navigation Satellite System. IEEE Trans. Aerosp. Electron. Syst. 2021. Early Access. [Google Scholar] [CrossRef]
- Kuchta, D.; Gryglewski, D.; Wojtasiak, W. A GaN HEMT Amplifier Design for Phased Array Radars and 5G New Radios. Micromachines 2020, 11, 398. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Lou, L.; Tang, K.; Wang, Y.; Gao, J.; Zheng, Y. A 13.5–19 GHz 20.6-dB Gain CMOS Power Amplifier for FMCW Radar Application. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 377–379. [Google Scholar] [CrossRef]
- Dmitriev, D.D.; Ratushnyak, V.N.; Gladyshev, A.B.; Tyapkin, V.N. Study of a Q-band Power Amplifier for Satellite Communication Systems. In Proceedings of the 2021 International Siberian Conference on Control and Communications (SIBCON), Kazan, Russian, 13–15 May 2021. [Google Scholar]
- Lee, M.-P.; Kim, S.; Hong, S.-J.; Kim, D.-W. Compact 20-W GaN Internally Matched Power Amplifier for 2.5 GHz to 6 GHz Jammer Systems. Micromachines 2020, 11, 375. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giofrè, R.; Colantonio, P.; Gonzalez, L.; Cabria, L.; De Arriba, F. A 300 W complete GaN solid-state power amplifier for positioning system satellite payloads. In Proceedings of the 2016 IEEE MTT-S International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016. [Google Scholar]
- Ma, J.; Zhou, S. Experimentally Investigating the Performance Degradations of Power Amplifiers Against Temperatures. In Proceedings of the 2020 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Guangzhou, China, 19–22 May 2020. [Google Scholar]
- Zhou, S. Experimental investigation on the performance degradations of the GaN class-F power amplifier under humidity conditions. Semicond. Sci. Technol. 2021, 36, 035025. [Google Scholar] [CrossRef]
- Gibiino, G.P.; Cappello, T.; Niessen, D.; Schreurs, D.M.M.-P.; Santarelli, A.; Filicori, F. An empirical behavioral model for RF PAs including self-heating. In Proceedings of the 2015 Integrated Nonlinear Microwave and Millimetre-Wave Circuits Workshop (INMMiC), Taormina, Italy, 1–2 October 2015; pp. 1–3. [Google Scholar]
- Jindal, G.; Watkins, G.T.; Morris, K.; Cappello, T. An RF Power Amplifier Behavioral Model with Low-Complexity Temperature Feedback for Transmitter Arrays. In Proceedings of the 2021 IEEE MTT-S International Microwave Symposium (IMS), Atlanta, GA, USA, 7–25 June 2021; pp. 442–445. [Google Scholar]
- Ali, K.M.; Sommet, R.; Mons, S.; Ngoya, E. Behavioral Electro-Thermal Modeling of Power Amplifier for System-Level Design. In Proceedings of the 2018 International Workshop on Integrated Nonlinear Microwave and Millimeter-wave Circuits (INMMIC), Brive La Gaillarde, France, 5–6 July 2018; pp. 1–3. [Google Scholar]
- Mazeau, J.; Sommet, R.; Caban-Chastas, D.; Gatard, E.; Quere, R.; Mancuso, Y. Behavioral Thermal Modeling for Microwave Power Amplifier Design. IEEE Trans. Microw. Theory Tech. 2007, 55, 2290–2297. [Google Scholar] [CrossRef]
- Subramaniyan, H.K.; Klumperink, E.A.M.; Srinivasan, V.; Kiaei, A.; Nauta, B. RF Transconductor Linearization Robust to Process, Voltage and Temperature Variations. IEEE J. Solid-State Circuits 2015, 50, 2591–2602. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Shi, C.-J.R. Design of the Class-E Power Amplifier Considering the Temperature Effect of the Transistor On-Resistance for Sensor Applications. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 1705–1709. [Google Scholar] [CrossRef]
- Sira, D.; Larsen, T. Process, Voltage and Temperature Compensation Technique for Cascode Modulated PAs. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 2511–2520. [Google Scholar] [CrossRef]
- Zhou, S.; Fu, H.; Ma, J.; Zhang, Q. A Neural Network Modeling Approach to Power amplifiers Taking into Account Temperature Effects. In Proceedings of the 2018 IEEE/MTT-S International Microwave Symposium-IMS, Philadelphia, PA, USA, 10–15 June 2018. [Google Scholar]
- Lin, Q.; Cheng, Q.F.; Gu, J.J.; Zhu, Y.Y.; Chen, C.; Fu, H.P. Design and Temperature Reliability Testing for A 0.6–2.14 GHz Broadband Power Amplifier. J. Electron. Test. 2016, 32, 235–240. [Google Scholar] [CrossRef]
- Chen, Y.L.; Yoshida, T.; Katayama, K.; Motoyoshi, M.; Fujishima, M. Evaluation of temperature dependence and lifetime of 79 GHz power amplifier. In Proceedings of the 2013 IEEE International Meeting for Future of Electron Devices, Kansai, Japan, 5–6 June 2013. [Google Scholar]
- Kumar, P.; Saurav, P.; Jaiswal, S.; Jalan, P.; Mehra, G. Temperature stable 65 nm UWB CMOS LNA with 1.5 dB NF for K-Band Applications. In Proceedings of the 2nd International Conference on Smart Electronics and Communication (ICOSEC), Trichy, India, 7–9 October 2021. [Google Scholar]
- Yang, C.; Feng, F. Multi-Step-Ahead Prediction for a CMOS Low Noise Amplifier Aging Due to NBTI and HCI Using Neural Networks. J. Electron. Test. 2019, 35, 797–808. [Google Scholar] [CrossRef]
- Xiao, L.; Shao, W.; Liang, T.; Wang, B. Efficient extreme learning machine with transfer functions for filter design. In Proceedings of the 2017 IEEE MTT-S International Microwave Symposium (IMS), Honolulu, HI, USA, 4–9 June 2017. [Google Scholar]
- Zhang, C.; Zhu, Y.; Cheng, Q.; Fu, H.; Ma, J.; Zhang, Q. Extreme learning machine for the behavioral modeling of RF power amplifiers. In Proceedings of the 2017 IEEE MTT-S International Microwave Symposium (IMS), Honolulu, HI, USA, 4–9 June 2017. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the. 2004 IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; pp. 985–990. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Tang, J.; Deng, C.; Huang, G. Extreme Learning Machine for Multilayer Perceptron. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 809–821. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.-B.; Zhou, H.; Ding, X.; Zhang, R. Extreme Learning Machine for Regression and Multiclass Classification. IEEE Trans. Syst. Man Cybern. 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Yuan, J. CMOS Transistor Amplifier Temperature Compensation: Modeling and Analysis. IEEE Trans. Device Mater. Reliab. 2012, 12, 376–381. [Google Scholar] [CrossRef]








| Number and Distribution of Measured Temperature Points | MSE | ||
|---|---|---|---|
| No. | Temperature (℃) | This Work | Ref. [19] |
| 3 | −40; 25; 90 | 9.2317 × 10−3 | 4.7517 × 10−1 |
| 3 | −40;−20; 90 | 9.3243 × 10−3 | 1.4372 × 100 |
| 5 | −40; −10; 25; 60; 90 | 9.1524 × 10−4 | 9.9561 × 10−2 |
| 5 | −40; −5; 0; 15; 90 | 9.2037 × 10−4 | 3.3107 × 10−1 |
| 6 | −40; −10; 15; 40; 65; 90 | 8.5972 × 10−4 | 9.6521 × 10−2 |
| 6 | −40; −20; 0; 70; 80; 90 | 8.6113 × 10−4 | 2.8317 × 10−1 |
| 7 | −40; −20; 0; 25; 50; 70; 90 | 8.3821 × 10−4 | 9.4621 × 10−2 |
| 7 | −40; −30; −20; 50; 60; 75; 90 | 8.4981 × 10−4 | 2.5237 × 10−1 |
| 8 | −40; −30; −10; 10; 30; 50; 70; 90 | 8.1681 × 10−5 | 9.2386 × 10−3 |
| 8 | −40; −35; −5; 15; 20; 25; 85; 90 | 8.2234 × 10−5 | 2.3025 × 10−2 |
| 9 | −40; −25; −10; 5; 25; 45; 60; 75; 90 | 7.8475 × 10−5 | 9.0274 × 10−3 |
| 9 | −40; −5; 10; 15; 35; 60; 65; 85; 90 | 8.0521 × 10−5 | 2.0679 × 10−2 |
| Number and Distribution of Measured Temperature Points | MSE | ||
|---|---|---|---|
| No. | Temperature (℃) | This Work | Ref. [19] |
| 3 | −40; 25; 90 | 8.8737 × 10−3 | 4.4758 × 10−1 |
| 3 | −40; 40; 90 | 9.0481 × 10−3 | 2.4478 × 100 |
| 5 | −40; −5; 25; 55; 90 | 8.6943 × 10−4 | 9.5745 × 10−2 |
| 5 | −40; 0; 25; 30; 90 | 8.7042 × 10−4 | 5.6612 × 10−1 |
| 6 | −40; −15; 10; 35; 60; 90 | 8.3569 × 10−4 | 9.3036 × 10−2 |
| 6 | −40; −20; −5; 20; 50; 90 | 8.4327 × 10−4 | 4.8756 × 10−1 |
| 7 | −40; −15; 5; 25; 45; 65; 90 | 7.9783 × 10−4 | 9.1069 × 10−2 |
| 7 | −40; −30; 0; 10; 40; 70; 90 | 8.1678 × 10−4 | 4.2132 × 10−1 |
| 8 | −40; −20; 0; 20; 40; 60; 80; 90 | 7.5237 × 10−5 | 8.8607 × 10−3 |
| 8 | −40; −25; −15; 0; 15; 35; 40; 90 | 7.6654 × 10−5 | 6.8072 × 10−2 |
| 9 | −40; −20; −5; 10; 25; 40; 55; 70; 90 | 7.0612 × 10−5 | 8.5492 × 10−3 |
| 9 | −40; −35; −5; 0; 15; 40; 65; 75; 90 | 7.1357 × 10−5 | 6.5627 × 10−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Yang, C.; Wang, J. Modeling of Key Specifications for RF Amplifiers Using the Extreme Learning Machine. Micromachines 2022, 13, 693. https://doi.org/10.3390/mi13050693
Zhou S, Yang C, Wang J. Modeling of Key Specifications for RF Amplifiers Using the Extreme Learning Machine. Micromachines. 2022; 13(5):693. https://doi.org/10.3390/mi13050693
Chicago/Turabian StyleZhou, Shaohua, Cheng Yang, and Jian Wang. 2022. "Modeling of Key Specifications for RF Amplifiers Using the Extreme Learning Machine" Micromachines 13, no. 5: 693. https://doi.org/10.3390/mi13050693
APA StyleZhou, S., Yang, C., & Wang, J. (2022). Modeling of Key Specifications for RF Amplifiers Using the Extreme Learning Machine. Micromachines, 13(5), 693. https://doi.org/10.3390/mi13050693