A New Analytical Model to Estimate the Voltage Value and Position of the Pull-In Limit of a MEMS Cantilever
Abstract
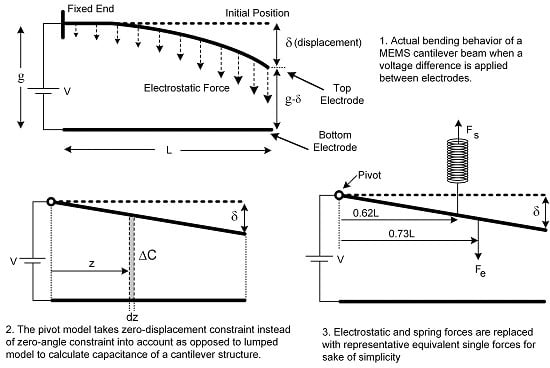
:1. Introduction
2. Lumped Model
3. Pivot Model
4. Positioning the Forces
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, Y.-T.; Hu, T.-C.; Tong, C.-J.; Lin, M.-T. Novel full range vacuum pressure sensing technique using free decay of trapezoid micro-cantilever beam deflected by electrostatic force. Microsyst. Technol. 2012, 18, 1903–1908. [Google Scholar] [CrossRef]
- Lindley, R.E.; Parkes, A.M.; Keen, K.A.; Mcnaghten, E.D.; Orr-Ewing, A.J. A sensitivity comparison of three photoacoustic cells containing a single microphone, a differential dual microphone or a cantilever pressure sensor. Appl. Phys. B 2007, 86, 707–713. [Google Scholar] [CrossRef]
- Lee, H.-C.; Park, J.-H.; Park, Y.-H. Development of shunt type ohmic RF MEMS switches actuated by piezoelectric cantilever. Sens. Actuators A Phys. 2007, 136, 282–290. [Google Scholar] [CrossRef]
- Zhang, Y.-H.; Ding, G.; Shun, X.; Gu, D.; Cai, B.; Lai, Z. Preparing of a high speed bistable electromagnetic RF MEMS switch. Sens. Actuators A Phys. 2007, 134, 532–537. [Google Scholar] [CrossRef]
- Hah, D.; Yoon, E. A Low-Voltage Actuated Micromachined Microwave Switch Using Torsion Springs and Leverage. IEEE Trans. Microw. Theory Technol. 2000, 48, 2540–2545. [Google Scholar]
- Chang, C.; Chang, P. Innovative micromachined microwave switch with very low insertion loss. Sens. Actuators A Phys. 2000, 79, 71–75. [Google Scholar] [CrossRef]
- Ozaki, Y.; Ohyama, T.; Yasuda, T.; Shimoyama, I. An Air Flow Sensor Modeled on Wind Receptor Hairs of Insects. In Proceedings of the 13th Annual International Conference on Micro Electro Mechanical Systems, Miyazaki, Japan, 23–27 January 2000; pp. 531–536.
- Wang, Y.-H.; Lee, C.-Y. A MEMS-based air flow sensor with a free-standing micro-cantilever structure. Sensors 2007, 7, 2389–2401. [Google Scholar] [CrossRef]
- Barth, S.; Koch, H.; Kittel, A.; Peinke, J.; Burgold, J.; Wurnus, H. Laser-Cantilever-Anemometer: A new high resolution sensor for air and liquid flow. Rev. Sci. Instrum. 2005, 76, 75110–75116. [Google Scholar] [CrossRef]
- Kamusuki, S.; Fujii, M.; Takekoshi, T.; Tezuka, C.; Atobe, M. A high resolution, electrostatically-driven commercial inkjet head. In Proceedings of the 13th Annual International Conference on Micro Electro Mechanical Systems, Miyazaki, Japan, 23–27 January 2000; pp. 793–798.
- Bietsch, A.; Zhang, J.; Hegner, M.; Lang, H.P.; Gerber, C. Rapid functionalization of cantilever array sensors by inkjet printing. Nanotechnology 2004, 15, 873–780. [Google Scholar] [CrossRef]
- Kaisei, K.; Kobayashi, K.; Matsushige, K.; Yamada, H. Fabrication of ionic liquid thin film by nano-inkjet printing method using atomic force microscope cantilever tip. Ultramicroscopy 2010, 110, 733–736. [Google Scholar] [CrossRef] [PubMed]
- Rogers, B.; Manning, L.; Jones, M.; Sulchek, T.; Murray, K.; Beneschott, B.; Adams, J.D.; Hu, Z.; Thundat, T.; Cavazos, H.; et al. Mercury vapor detection with a self-sensing, resonating piezoelectric cantilever. Rev. Sci. Instrum. 2003, 74, 4899–4901. [Google Scholar] [CrossRef]
- Lavrik, N.V.; Sepaniak, M.J.; Datskos, P.G. Cantilever transducers as a platform for chemical and biological sensors. Rev. Sci. Instrum. 2004, 75, 2229–2251. [Google Scholar] [CrossRef]
- Sharma, H.; Mutharasan, R. Rapid and sensitive immune detection of Listeria monocytogenes in milk using a novel piezoelectric cantilever sensor. Biosens. Bioelectron. 2013, 45, 158–162. [Google Scholar] [CrossRef] [PubMed]
- Saadon, S.B.; Sidek, O.B.; Hamad, O.S. Vibration-based MEMS piezoelectric energy harvesters using cantilever beams. Optoelectron. Adv. Mater. Rapid Commun. 2010, 4, 1219–1224. [Google Scholar]
- Shen, D.; Park, J.-H.; Ajitsaria, J.; Choe, S.-Y.; Wikle III, H.C.; Kim, D.J. The design, fabrication and evaluation of a MEMS PZT cantilever with an integrated Si proof mass for vibration energy harvesting. J. Micromech. Microeng. 2008, 18, 55017. [Google Scholar] [CrossRef]
- Yu, H.; Zhou, J.; Deng, L.; Wen, Z. A Vibration-Based MEMS Piezoelectric Energy Harvester and Power Conditioning Circuit. Sensors 2014, 14, 3323–3341. [Google Scholar] [CrossRef] [PubMed]
- Dequesnes, M.; Rotkin, S.V.; Aluru, N.R. Calculation of pull-in voltages for carbon-nanotube-based nanoelectromechanical swithes. Nanotechnology 2002, 13, 120–131. [Google Scholar] [CrossRef]
- Seeger, J.I.; Boser, B.E. Dynamics and Control of Parallel-Plate Actuators Beyond the Electrostatic Instability. In Proceedings of the 10th International Conference on Solid-State Sensors and Actuators, Sendai, Japan, 7–9 June 1999; pp. 474–477.
- Nielson, G.N.; Barbastathis, G. Dynamic Pull-in of Parallel-Plate and Torsional Electrostatic MEMS Actuators. J. Microelectromech. Syst. 2006, 15, 811–821. [Google Scholar] [CrossRef]
- Pamidighantam, S.; Puers, R.; Baert, K.; Tilmans, H.A. Pull-in voltage analysis of electrostatically actuated beam structures with fixed–fixed and fixed–free end conditions. J. Micromech. Microeng. 2002, 12, 458–464. [Google Scholar] [CrossRef]
- Mol, L.; Rocha, L.A.; Cretu, E.; Wolffenbuttel, R.F. Full-Gap Positioning of Parallel-Plate Electrostatic MEMS Using On-off Control. In Proceedings of the IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; pp. 1464–1468.
- Chowdhury, S.; Ahmadi, M.; Miller, W.C. Pull-in Voltage Study of Electrostatically Actuated Fixed-Fixed Beams Using a VLSI On-Chip Interconnect Capacitance Model. J. Microelectromech. Syst. 2006, 15, 639–651. [Google Scholar] [CrossRef]
- Owusu, K.O.; Lewis, F.L. Solving the Pull-in Instability Problem of Electrostatic Microactuators Using Nonlinear Control Techniques. In Proceedings of the 2nd IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Bangkok, Thailand, 16–19 January 2007; pp. 1190–1195.
- Hu, Y.C.; Chang, C.M.; Huang, S.C. Some design considerations on the electrostatically actuated microstructures. Sens. Actuators A Phys. 2004, 112, 155–161. [Google Scholar] [CrossRef]
- Sadeghian, H.; Rezazadeh, G.; Osterberg, P.M. Application of the Generalized Differential Quadrature Method to the Study of Pull-in Phenomena of MEMs Switches. J. Microelectromech. Syst. 2007, 16, 1334–1340. [Google Scholar] [CrossRef]
- Chowdhury, S.; Ahmadi, M.; Miller, W.C. A Closed-Form Model for the Pull-in Voltage of Electrostatically Actuated Cantilever Beams. J. Micromech. Microeng. 2005, 15, 756–763. [Google Scholar] [CrossRef]
- O’Brien, G.J.; Monk, D.J.; Lin, L. MEMS Cantilever Beam Electrostatic Pull-in Model. Proc. SPIE 2001, 4593, 31–34. [Google Scholar]
- Nathanson, H.C.; Nevel, W.E.; Wickstrom, R.A.; Davis, J.R., Jr. The resonant gate transistor. IEEE Trans. Electron. Devices 1967, 14, 117–133. [Google Scholar] [CrossRef]
- Yildiz, A.; Ak, C.; Canbolat, H. New Approach to Pull-In Limit and Position Control of Electrostatic Cantilever Within the Pull-in Limit. In Electrostatics; Canbolat, H., Ed.; Intech: Rijeka, Croatia, 2012; pp. 139–150. [Google Scholar]
- Ak, C. Position Control of Electrostatic Actuators. Master’s Thesis, Mersin University, Mersin, Turkey, 2008. [Google Scholar]
- Ak, C.; Yildiz, A. An Inversely Designed Model for Calculating Pull-In Limit and Position of Electrostatic Fixed-Fixed Beam Actuators. Math. Probl. Eng. 2014, 2014, 391942. [Google Scholar] [CrossRef]
- Saha, S.C.; Hanke, U.; Jensen, G.U.; Saether, T. Modeling of spring constant and pull-down voltage of non-uniform RF MEMS cantilever. In Proceedings of the 2006 IEEE International Behavioral Modeling and Simulation Workshop, San Jose, CA, USA, 14–15 September 2006; pp. 56–60.
- Ozdemir, S.; Akhtar, S.; Gunal, O.E.; Khater, M.E.; Saritas, R.; Abdel-Rahman, E.M.; Yavuz, M. Measuring the Quality Factor in MEMS Devices. Micromachines 2015, 6, 1935–1945. [Google Scholar] [CrossRef]
- Palevicius, P.; Ragulskis, M.; Palevicius, A.; Ostasevicius, V. Applicability of Time-Averaged Holography for Micro-Electro-Mechanical System Performing Non-Linear Oscillations. Sensors 2014, 14, 1805–1821. [Google Scholar] [CrossRef] [PubMed]
- Sharpe, W.N., Jr.; Yuan, B.; Vaidyanathan, R.; Edward, R.L. Measurements of Young’s modulus, Poisson’s ratio, and tensile strength of polysilicon. Nagoya, Japan, 26–30 January 1997; pp. 424–429.
- Osterberg, P.M.; Senturia, S.D. M-Test: A Test Chip for MEMS Material Property Measurement Using Electrostatically Actuated Test Structures. J. Microelectromech. Syst. 1997, 6, 107–118. [Google Scholar] [CrossRef]






| Initial Gap (µm) | ANSYS Pull-In Gap (µm) | ANSYS Pull-In Gap/Initial Gap | COMSOL Pull-In Gap (µm) | COMSOL Pull-In Gap/Initial Gap |
|---|---|---|---|---|
| 2 | 0.881 | 0.4405 | 0.884 | 0.4420 |
| 4 | 1.761 | 0.4403 | 1.769 | 0.4422 |
| 5 | 2.202 | 0.4404 | 2.212 | 0.4424 |
| 10 | 4.403 | 0.4403 | 4.424 | 0.4424 |
| 20 | 8.809 | 0.4405 | 8.848 | 0.4424 |
| COMSOL for CWBE | Empirical Vmax (V) [29] | Vmax (V) [29]/% Error (CWBE)/% Error (Empirical Result) | Pivot Model/% Error (CWBE)/% Error (Empirical Result) |
|---|---|---|---|
| 18.30 | 17.60 | 19.18/4.81/8.98 | 21.97/20.05/24.83 |
| COMSOL | Vmax (V) [29]/% Error | Pivot Model/% Error |
|---|---|---|
| 21.17 | 19.18/9.40 | 21.97/3.78 |
| Cantilever Length (µm) | Vmax (V) Pivot Model | Vmax (V) (ANSYS) | % Error of the Model with Respect to ANSYS | Vmax (V) (COMSOL) | % Error of the Model with Respect to COMSOL |
|---|---|---|---|---|---|
| 150 | 26.619 | 27.341 | 2.712 | 27.070 | 1.694 |
| 200 | 14.973 | 15.418 | 2.972 | 15.240 | 1.783 |
| 250 | 9.583 | 9.899 | 3.298 | 9.760 | 1.847 |
| 300 | 6.655 | 6.828 | 2.600 | 6.780 | 1.878 |
| 400 | 3.743 | 3.860 | 3.126 | 3.820 | 2.057 |
| 500 | 2.396 | 2.472 | 3.172 | 2.450 | 2.254 |
| Displacement (µm) and (δ/g) | Voltage (V) Pivot Model | Voltage (V) (ANSYS) | % Error of the Model with Respect to ANSYS | Voltage (V) (COMSOL) | % Error of the Model with Respect to COMSOL |
|---|---|---|---|---|---|
| 0.05829 (2.91%) | 9.797 | 10.0 | 2.075 | 9.85 | 0.544 |
| 0.1386 (6.93%) | 14.689 | 15.0 | 2.119 | 14.78 | 0.621 |
| 0.2714 (13.57%) | 19.574 | 20.0 | 2.178 | 19.72 | 0.747 |
| 0.5165 (25.83%) | 24.431 | 25.0 | 2.328 | 24.68 | 1.018 |
| 0.6028 (30.14%) | 25.387 | 26.0 | 2.414 | 25.70 | 1.233 |
| 0.7419 (37.10%) | 26.324 | 27.0 | 2.566 | 26.69 | 1.389 |
| 0.7654 (38.27%) | 26.417 | 27.1 | 2.586 | 26.80 | 1.450 |
| 0.7963 (39.82%) | 26.512 | 27.2 | 2.597 | 26.91 | 1.503 |
| 0.8146 (40.73%) | 26.553 | 27.25 | 2.624 | 26.97 | 1.569 |
| 0.8808 (44.04%) | 26.619 | 27.341 | 2.712 | 27.07 | 1.694 |
| Voltage (V) | Experimental (µm) [26] | Distributed Model (µm) [26]/(Error) | GDQM (µm) [27]/(Error) | Pivot Model (µm)/(Error) | ANSYS (µm) |
|---|---|---|---|---|---|
| 20 | 90.5 | 90.2/(0.3%) | 90.2/(0.3%) | 90.3/(0.2%) | 90.4 |
| 40 | 84.6 | 84.3/(0.4%) | 84.1/(0.6%) | 84.7/(0.1%) | 85.1 |
| 60 | 70.0 | 71.5/(2.1%) | 69.1/(1.3%) | 71.3/(1.9%) | 73.2 |
| 65 | 64.0 | 67.2/(5.0%) | 59.6/(6.9%) | 64.1/(0.2%) | 67.6 |
| 67 | 59.0 | 65.0/(10.2%) | - | 59.1/(0.2%) | 64.5 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ak, C.; Yildiz, A. A New Analytical Model to Estimate the Voltage Value and Position of the Pull-In Limit of a MEMS Cantilever. Micromachines 2016, 7, 53. https://doi.org/10.3390/mi7040053
Ak C, Yildiz A. A New Analytical Model to Estimate the Voltage Value and Position of the Pull-In Limit of a MEMS Cantilever. Micromachines. 2016; 7(4):53. https://doi.org/10.3390/mi7040053
Chicago/Turabian StyleAk, Cevher, and Ali Yildiz. 2016. "A New Analytical Model to Estimate the Voltage Value and Position of the Pull-In Limit of a MEMS Cantilever" Micromachines 7, no. 4: 53. https://doi.org/10.3390/mi7040053
APA StyleAk, C., & Yildiz, A. (2016). A New Analytical Model to Estimate the Voltage Value and Position of the Pull-In Limit of a MEMS Cantilever. Micromachines, 7(4), 53. https://doi.org/10.3390/mi7040053