3D Finite Element Simulation of Graphene Nano-Electro-Mechanical Switches
Abstract
:1. Introduction
2. Description of the Device Geometry
3. Finite Element Method Simulation Results and Discussion
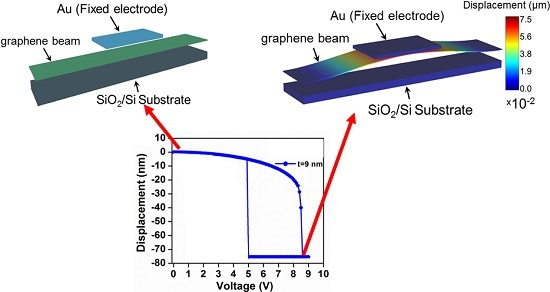
3.1. Graphene NEM Switch Pull-In and Pull-Out Characteristics
3.2. Von Mises Stress Analysis
3.3. Three-Dimensional Electric Field Distribution and Its Role in Graphene Beam NEM Switch Operation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chui, C.O.; Shih, K.H.; Shoorideh, K. Low Dissipation Nanoscale Transistor Physics and Operations. In Proceedings of the 9th International Conference on Solid-State and Integrated-Circuit Technology (ICSICT 2008), Beijing, China, 22–23 October 2008; pp. 29–32.
- Peschot, A.; Qian, C.; Liu, T.-J.K. Nanoelectromechanical switches for low-power digital computing. Micromachines 2015, 6, 1046–1065. [Google Scholar] [CrossRef]
- Dadgour, H.F.; Banerjee, K. Design and Analysis of Hybrid NEMS-CMOS Circuits for Ultra Low-Power Applications. In Proceedings of the 44th ACM/IEEE Design Automation Conference, San Diego, CA, USA, 4–8 June 2007; pp. 306–311.
- Loh, O.Y.; Espinosa, H.D. Nanoelectromechanical contact switches. Nat. Nanotechnol. 2012, 7, 283–295. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.-H.; Bhunia, S.; Mehregany, M. Electromechanical computing at 500 °C with silicon carbide. Science 2010, 329, 1316–1318. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.-J.; Ahn, J.-H.; Han, J.-W.; Seol, M.-L.; Moon, D.-I.; Kim, S.; Choi, Y.-K. Transformable functional nanoscale building blocks with wafer-scale silicon nanowires. Nano Lett. 2011, 11, 854–859. [Google Scholar] [CrossRef] [PubMed]
- Loh, O.; Wei, X.; Sullivan, J.; Ocola, L.E.; Divan, R.; Espinosa, H.D. Carbon-Carbon contacts for robust nanoelectromechanical switches. Adv. Mater. 2012, 24, 2463–2468. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; You, Z.; Haugstad, G.; Cui, T. Graphene fixed-end beam arrays based on mechanical exfoliation. Appl. Phys. Lett. 2011, 98, 253105. [Google Scholar] [CrossRef]
- Liu, X.; Suk, J.W.; Boddeti, N.G.; Cantley, L.; Wang, L.; Gray, J.M.; Hall, H.J.; Bright, V.M.; Rogers, C.T.; Dunn, M.L.; et al. Large arrays and properties of 3-terminal graphene nanoelectromechanical switches. Adv. Mater. 2014, 26, 1571–1576. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Wang, W.; Muruganathan, M.; Mizuta, H. Low pull-in voltage graphene electromechanical switch fabricated with a polymer sacrificial spacer. Appl. Phys. Lett. 2014, 105, 33103. [Google Scholar] [CrossRef]
- Sun, J.; Schmidt, M.E.; Muruganathan, M.; Chong, H.M.H.; Mizuta, H. Large-scale nanoelectromechanical switches based on directly deposited nanocrystalline graphene on insulating substrates. Nanoscale 2016, 8, 6659–6665. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.E.; Xu, C.; Cooke, M.; Mizuta, H.; Chong, H.M.H. Metal-free plasma-enhanced chemical vapor deposition of large area nanocrystalline graphene. Mater. Res. Express 2014, 1, 25031. [Google Scholar] [CrossRef]
- Wu, J.; Wei, Y. Grain misorientation and grain-boundary rotation dependent mechanical properties in polycrystalline graphene. J. Mech. Phys. Solids 2013, 61, 1421–1432. [Google Scholar] [CrossRef]
- Song, Z.; Artyukhov, V.I.; Yakobson, B.I.; Xu, Z. Pseudo hall–petch strength reduction in polycrystalline graphene. Nano Lett. 2013, 13, 1829–1833. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Wu, J.; Yin, H.; Shi, X.; Yang, R.; Dresselhaus, M. The nature of strength enhancement and weakening by pentagon–heptagon defects in graphene. Nat. Mater. 2012, 11, 759–763. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Huang, Y.; Ma, F.; Sun, Y.; Xu, K.; Chu, P.K. Size-dependent deformation behavior of nanocrystalline graphene sheets. Mater. Sci. Eng. B 2015, 198, 95–101. [Google Scholar] [CrossRef]
- Zhang, T.; Li, X.; Kadkhodaei, S.; Gao, H. Flaw insensitive fracture in nanocrystalline graphene. Nano Lett. 2012, 12, 4605–4610. [Google Scholar] [CrossRef] [PubMed]
- Shekhawat, A.; Ritchie, R.O. Toughness and strength of nanocrystalline graphene. Nat. Commun. 2016, 7, 10546. [Google Scholar] [CrossRef] [PubMed]
- Frank, I.W.; Tanenbaum, D.M.; van der Zande, A.M.; McEuen, P.L. Mechanical properties of suspended graphene sheets. J. Vac. Sci. Technol. B 2007, 25, 2558–2561. [Google Scholar] [CrossRef]
- Zhang, W.-M.; Yan, H.; Peng, Z.-K.; Meng, G. Electrostatic pull-in instability in MEMS/NEMS: A review. Sens. Actuators Phys. 2014, 214, 187–218. [Google Scholar] [CrossRef]
- IntelliSense-Total MEMS Solutions-IntelliSuite Software. Available online: http://www.intellisense.com (accessed on 11 August 2016).
- Beer, F. Mechanics of Materials, 2nd ed.; McGraw Hill: New York, NY, USA, 2002. [Google Scholar]
- Young, W.C. Roak’s Formulas for Stress and Strain, 7th ed.; McGraw Hill: New York, NY, USA, 2002. [Google Scholar]
- Kim, D.H.; Kim, M.W.; Jeon, J.W.; Lim, K.S.; Yoon, J.B. Mechanical Reliability of a digital micromirror with interdigitated cantilevers. J. Microelectromechanical Syst. 2010, 19, 1197–1206. [Google Scholar] [CrossRef]
- Boldeiu, G.; Vasilache, D.; Moagar, V.; Stefanescu, A.; Ciuprina, G. Study of the von Mises Stress in RF MEMS Switch Anchors. In Proceedings of the 2015 International Semiconductor Conference (CAS), Sinaia, Rome, 12–14 October 2015; pp. 219–222.
- COMSOL Multiphysics® and COMSOL Server™. Available online: http://www.comsol.com (accessed on 11 August 2016).
- Kambali, P.N.; Pandey, A.K. Capacitance and Force Computation Due to Direct and Fringing Effects in MEMS/NEMS Arrays. IEEE Sens. J. 2016, 16, 375–382. [Google Scholar] [CrossRef]







| NEM Switch | Dimension | Air Gap Thickness (nm) | ||
|---|---|---|---|---|
| Length (μm) | Width (μm) | Thickness (nm) | ||
| A | 1.5 | 0.5 | 9 | 75 |
| B | 1 | 0.5 | 9 | 50 |
| C | 0.8 | 0.5 | 9 | 45 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulothungan, J.; Muruganathan, M.; Mizuta, H. 3D Finite Element Simulation of Graphene Nano-Electro-Mechanical Switches. Micromachines 2016, 7, 143. https://doi.org/10.3390/mi7080143
Kulothungan J, Muruganathan M, Mizuta H. 3D Finite Element Simulation of Graphene Nano-Electro-Mechanical Switches. Micromachines. 2016; 7(8):143. https://doi.org/10.3390/mi7080143
Chicago/Turabian StyleKulothungan, Jothiramalingam, Manoharan Muruganathan, and Hiroshi Mizuta. 2016. "3D Finite Element Simulation of Graphene Nano-Electro-Mechanical Switches" Micromachines 7, no. 8: 143. https://doi.org/10.3390/mi7080143
APA StyleKulothungan, J., Muruganathan, M., & Mizuta, H. (2016). 3D Finite Element Simulation of Graphene Nano-Electro-Mechanical Switches. Micromachines, 7(8), 143. https://doi.org/10.3390/mi7080143