Names for Games: Locating 2 × 2 Games ^†

Abstract

Prisoner’s Dilemma, Chicken, Stag Hunts, and other two-person two-move (2 × 2) models of strategic situations have played a central role in the development of game theory. The Robinson–Goforth topology of payoff swaps reveals a natural order in the payoff space of 2 × 2 games, visualized in their four-layer “periodic table” format that elegantly organizes the diversity of 2 × 2 games, showing relationships and potential transformations between neighboring games. This article presents additional visualizations of the topology, and a naming system for locating all 2 × 2 games as combinations of game payoff patterns from the symmetric ordinal 2 × 2 games. The symmetric ordinal games act as coordinates locating games in maps of the payoff space of 2 × 2 games, including not only asymmetric ordinal games and the complete set of games with ties, but also ordinal and normalized equivalents of all games with ratio or real-value payoffs. An efficient nomenclature can contribute to a systematic understanding of the diversity of elementary social situations; clarify relationships between social dilemmas and other joint preference structures; identify interesting games; show potential solutions available through transforming incentives; catalog the variety of models of 2 × 2 strategic situations available for experimentation, simulation, and analysis; and facilitate cumulative and comparative research in game theory.

1. Introduction

Two-person, two-move games form the simplest possible models of strategic situations, where the outcomes of each person’s action depend on choices by another. Prisoner’s Dilemma, Chicken (also known as Hawk-Dove), and other 2 × 2 preference structures have played a central role in the development and application of game theory in economics, political science, evolutionary biology, and other fields. Most attention has focused on a small subset of strict symmetric games, with less attention to the much larger numbers of asymmetric games, where players do not face the same incentive structure, and to non-strict games, those with indifference (ties) between outcomes. Games have mostly been looked at in isolation, assuming static preferences, with limited consideration of how changes in payoffs may transform one incentive structure into another [2,3,4,5].

Even for 2 × 2 ordinal games, with only two players, two choices, and four ranked payoffs, the multitude of apparently different payoff structures for games can make it hard to understand the diversity of games and difficult to identify games that are similar or equivalent. Taxonomies and associated naming systems have played a significant role in organizing knowledge in many fields of science, such as the Periodic Table of the Elements, molecular names in chemistry, and Linnaean classification of species, but have not seen much application in game theory. Rapoport and Guyer [6] showed that for strict ordinal games, where each player has four differently ranked payoffs, there are 78 strategically distinct games, when payoff matrices formed by switching columns, rows, or positions (as row or column player) are treated as equivalent. They proposed a Linnaean-style branching taxonomy, based on properties including conflict, dominant strategies, Pareto-inferiority, and a concept of “natural outcomes” related to maximin strategies, pressure, and vulnerability to competition and threats. They analyzed the available research on 2 × 2 ordinal games, and provided an appendix with game numbers and payoff matrices. However, their taxonomy and game numbers have seen little subsequent use. A subsequent typology and alternative numbering scheme for strict ordinal 2 × 2 games (omitting “no conflict” games) developed as part of Brams’ Theory of Moves [7] has also seen little use by other authors.

If ties are allowed, then there are 726 strategically unique ordinal games [8]. Kilgour and Fraser noted that little attention had been paid to games with ties (non-strict), in part due to the large number of such games. In addition to strict games without ties, there are seven possible types of ties, creating eight preference orderings [8,9,10]. Fraser and Kilgour used a computer program to enumerate the complete set of 2 × 2 ordinal games and analyze their properties. Since they were not aware of any “natural order” in the 2 × 2 games, they used a somewhat arbitrary numbering scheme. Although they expressed the hope that their work would contribute to further work on games with ties, and expressed a willingness to share their detailed output and program code, their numbering system does not seem to have been further applied.

Robinson and Goforth [2] showed that swaps in adjoining payoffs link 2 × 2 strict ordinal games in a topology, as for example when swaps in the highest payoffs convert Prisoner’s Dilemma into Stag Hunt. This topology reveals a natural order in the payoff space of 2 × 2 games. Their “periodic table” display elegantly arranges 2 × 2 symmetric and asymmetric strict ordinal games in cross-cutting categories according to alignment of best payoffs, symmetry, number of dominant strategies and equilibria, externalities (inducement correspondences [11]), kinds of conflict (including zero-sum, pure cooperation, and mixed interests [12]), the presence of Pareto-inferior equilibria, and other properties. In their table, index numbers identify the strict 2 × 2 ordinal games, including pairs of games equivalent by swapping row and column positions. However, the way the numbers were initially assigned and the table adjusted to show game properties means that the sequence of index numbers is not obvious or intuitive, and instead requires some understanding of the structure of the topology. Robinson and Goforth’s game numbers do not seem to have seen much use in the ten years since their book was published.

The topology of 2 × 2 strict ordinal games can be expanded to include games with ties, with transformations that make or break ties treated as half-swaps [13,14,15]. Many more games have equivalent ordinal structures, so each ordinal game represents a much larger equivalence set of games with payoffs measured on ratio (interval) or real (cardinal) scales [2]. Normalized versions of symmetric games with real or ratio payoffs may be mapped onto a topology of the symmetric 2 × 2 games [4,5] and normalized versions of symmetric and asymmetric games may be similarly mapped onto the full topology of 2 × 2 games [16]. Thus, the topology of 2 × 2 games provides a unifying framework for understanding relationships between all 2 × 2 games.

While the author was developing additional visualizations of the topology of payoff swaps in 2 × 2 games, it became apparent that a simple naming scheme could be applied to locate games within these maps of payoff space. Each row has the same payoff pattern for the row player and each column has the same pattern for the column player. The strict symmetric games form a diagonal axis in the table. Thus, each asymmetric game combines payoff patterns from two different symmetric games, providing a way to specify the location, and a name, for each asymmetric game. The same approach extends to the games with ties, which requires first identifying all the symmetric 2 × 2 ordinal games with ties. Games with ties can be treated as transformations of games without ties, so names for twelve strict games and seven transformations suffice to name all the ordinal 2 × 2 games and locate them within the topology of 2 × 2 games.

Changes in expected payoffs are a common occurrence in strategic situations; as a result of better information, technological innovation, agreements with side payments, rules with sanctions, sympathy and other revisions in preferences, and other processes, and may switch the relative ranking of different outcomes, creating payoff swaps [2]. Changing rules and other institutions to modify incentives can be crucial to solving social dilemmas and other problems of collective action [17]. The nomenclature and maps of the topology of payoff swaps locate games and show their potential transformations, contributing to a dynamic understanding of how social situations may change. A nomenclature based on the topology of payoff swaps in 2 × 2 games contributes to a systematic understanding of the diversity of 2 × 2 games, putting the few highly-studied strict symmetric games into the larger context of the full range of elementary models of social situations. The nomenclature catalogs the many possible models available for research, including experiments, simulations, and analysis; and should facilitate comparative and cumulative research in game theory and related fields.

The next section of the paper briefly introduces the topology of 2 × 2 games and presents results including additional visualizations of the payoff space of 2 × 2 games, a nomenclature for locating games within the topology, the complete set of 38 strategically distinct 2 × 2 symmetric ordinal games, and the extension of the nomenclature to ordinal games with ties. The following section discusses how the nomenclature may be useful in identifying games that are equivalent or similar; distinguishing between similar games, such as different types of Stag Hunts and Cyclic Games; understanding relationships between games, such as the Volunteer’s Dilemma and Low Dilemma games that adjoin Chicken, and identifying interesting games for further study. Methods used in developing the nomenclature for locating games within the payoff space of 2 × 2 strategic situations are then described, followed by a brief summary of conclusions.

2. Results

2.1. Visualizing the Payoff Space of 2 × 2 Games

The topology of payoff swaps provides a natural ordering for arranging the 2 × 2 games, assuming that games linked by swaps in the lowest payoffs are nearest neighbors [2]. Four games linked by swaps in the two lowest payoffs (1↔2) form a tile. Tiles are linked by swaps in middle payoffs (2↔3), forming a layer of 9 tiles and 36 games. Swaps in the two highest payoffs (3↔4) link games across layers. While the full topology linking games in a network forms a three-dimensional torus with 37 holes, the payoff space can be conveniently displayed on a two-dimensional surface divided into four “layers.” Layers differ by the alignment of best payoffs, as shown in Figure 1 and Figure 2, which are enhanced visualizations of the topology of payoff swaps in 2 × 2 games, building on Robinson and Goforth’s Periodic Table format [18].

The twelve strict symmetric games form a diagonal axis from lower left to upper right. Games on Layer 1 have best payoffs in diagonally opposed cells, while those on Layer 3 have win–win outcomes with the best payoffs in the same cell. Each layer is a torus, and wraps from left to right and top to bottom. With Prisoner’s Dilemma scrolled toward the center, the entire table is also a torus that wraps from left-to-right and top-to-bottom, showing links from swaps of best and second-best payoffs (3↔4) that cross between layers, including, for example, the swaps that transform Prisoner’s Dilemma into Stag Hunt.

Within each layer, games in the lower left quadrant have two dominant strategies and a single Nash Equilibrium. Games in the adjoining quadrants, above and to the right, have one dominant strategy and a single Nash Equilibrium. Games in the upper right quadrant have no dominant strategies, with cyclic games (with no Nash Equilibria in pure strategies) on Layers 2 and 4, while stag hunts on Layer 3 and battles on Layer 1 both have two Nash Equilibria.

Robinson and Goforth’s Periodic Table of 2 × 2 Ordinal Games showed game payoff structures as graphs. The additional visualization (presented in Table 2 [18]) shows numeric payoffs as an alternative that may be easier to use for those to whom the payoff graphs are not intuitive. Robinson and Goforth identified families of games including win–win games, (with a subset of stag hunts); games where following a dominant strategy leads to a Pareto-inferior equilibrium, as in Prisoner’s Dilemma and its asymmetric siblings and cousins; varieties of Battle of the Sexes; and cyclic games. These form compact connected regions in the topology. The visualization presented here provides a complete set of families, based on payoffs at Nash Equilibria, shown in different colors (with shading for subfamilies with different numbers of dominant strategies), including win–win, social traps, battles, and cyclic games, and adding several more payoff families: second-best (3,3); biased (4,3); unfair (4,2); and sad games (3,2) without a Pareto-superior outcome.

Figure 1. In the Topology of 2 × 2 Games, swaps in adjoining payoffs link strict ordinal games. Based on [2] and [18].

Figure 1. In the Topology of 2 × 2 Games, swaps in adjoining payoffs link strict ordinal games. Based on [2] and [18].

Figure 2. The twelve strict symmetric games form a diagonal axis in this small schematic diagram of the Topology of 2 × 2 Games.

Figure 2. The twelve strict symmetric games form a diagonal axis in this small schematic diagram of the Topology of 2 × 2 Games.

This visualization includes borderlines separating games. Narrow borderlines separate games within the same tile. Borderlines mark the locations of games with ties that lie between the strict ordinal games, as discussed later. Intersections in the grid of borderlines mark the location of ordinal games with ties for both players. Thicker borderlines outline tiles of games, and form horizontal and vertical bands composed of three tiles. Bands share similar high swap (3↔4) linkages between equivalently-located tiles on different layers. Icons on the edges of the table indicate the pattern of payoff ranks for rows and columns of strict ordinal games. Pairs of arrows on the edges show the structure of games with dominant strategies for row or column, for each quadrant within a layer.

2.2. Names for Strict Ordinal 2 × 2 Games

The strict symmetric games lie along a diagonal axis in the Topology of 2 × 2 games, as shown in Figure 1 and in the schematic visualization of the topology in Figure 2. Payoffs are the same across each row for the row player and in each column for the column player, so payoff patterns from two symmetric games combine to form the bimatrix payoff structure for each asymmetric game, providing an efficient way to locate and name games. The nomenclature requires specifying unique names for each of the twelve strict games, as further described in the Methods section. Where games have been discussed under multiple names, and for asymmetric games with established names, those can be treated as a “common name,” with the formal name used as a “scientific name” analogous to Linnaean taxonomy, for example Samaritan’s Dilemma [19] (Harmony × Chicken). This binomial nomenclature conveniently locates each game in relation to neighboring games in the topology of 2 × 2 games.

Games in the table are symmetric around the diagonal axis, equivalent by switching position as row or column, and this naming system names make these mirror pairs obvious. In Figure 1, the games below the axis show common names for selected games. Many of these are based on earlier research, as in the Robinson–Goforth Periodic Table of 2 × 2 games [18], which in turn draws heavily on names from Brams’ research on 2 × 2 games [7], while others are suggested by characteristics of games that may be of interest. Abbreviations provide a compact notation for identifying games, thus Samaritan’s Dilemma would be HaCh.

2.3. The Complete Set of Symmetric Games with Ties

Extending the naming scheme to games with ties requires identifying and assigning unique names to all symmetric 2 × 2 games with ties. Fraser and Kilgour generated the complete set of all 2 × 2 strategically distinct ordinal 2 × 2 games [10], which would have included all the symmetric 2 × 2 ordinal games, although they did not publish the actual payoff structures. Subsequent publications by other researchers have shown the complete set of symmetric 2 × 2 ordinal games in a diagram using payoff graphs [4] and discussed them [5]. However, the complete set of 38 symmetric ordinal games does not appear to have been previously published in normal form matrices, as shown in the lower section of Figure 1, including the 26 strategically distinct 2 × 2 symmetric ordinal games with ties. Games with ties can be categorized according to the number and type of ties [9,10]. In addition to the strict games with no ties, games may have two ties for the lowest, middle, or highest payoffs; two pairs of ties; three ties for highest or lowest payoffs; or all ties.

Creating ties in the twelve strict games forms symmetric games with ties. The names of the adjoining strict games can be used to assign identifying names to the symmetric games with ties, as further discussed in the methods section. As an example, Volunteer’s Dilemma, located between Chicken and Battle would be Middle Battle. The 12 strict symmetric ordinal games and 26 symmetric ordinal games with ties (including the Zero “game” of complete indifference) compose a total of 38 strategically unique symmetric ordinal games. The Supplementary Materials for this paper include cards showing graphs, numeric payoffs, and other properties for each of the symmetric 2 × 2 ordinal games.

2.4. Locating Asymmetric Games with Ties

In the expanded topology of 2 × 2 games, most classes of games form compact rectangular matrices of games in which each game only appears once, as shown in Figure 3 and so can easily be assigned unique names in the same way as for strict games. However, games with ties for the two highest payoffs, High Ties and Double Ties along with the Zero game, require additional specifications. Matrices for these games contain alternate variants, equivalent by row and column swaps. Some of those alternate payoff structures for symmetric games are needed to form some of the asymmetric games, such as Matching Pennies (Double Coordination × Double Hero). As discussed in the methods section, versions in the lower left (win–win) Layer 3 can be designated as default versions, as indicated in Figure 3.

2.5. A Binomial Nomenclature for 2 × 2 Ordinal Games

All 2 × 2 ordinal games can be named and located within the topology of 2 × 2 games based on how they combine payoff patterns from the 2 × 2 symmetric ordinal games, with some additional specifications for games with ties on the two highest payoffs. As discussed in the methods section, variants equivalent by row and column swaps can be distinguished according to the location of the highest payoffs, for example following Robinson and Goforth’s convention of putting the highest row payoff in the right-hand column and the highest column payoff in the upper row, with variants designated using subscripts. Appropriate choice of names for games and types of ties allows compact abbreviations, which could also be used as the basis for short distinct hashtags (for example #2×2pd) and for unique resource identifiers (URIs) for 2 × 2 games in a semantic web [20] ontology. Each ordinal game represents an equivalence set of games with the same ordinally-ranked payoffs measured on ratio or real scales. A simple procedure can be used to find the ordinal equivalent for any 2 × 2 game. Normalized equivalents of games with ratio and real payoff values can also be mapped onto the topology. Thus, the tables show not only the ordinal games, with discrete payoffs, including games with ties at grid intersections, but also map a flat (2-dimensional) projection of the normalized payoffs for the continuous payoff space of the topology of payoff swaps for all 2 × 2 games. A binomial nomenclature based on the topology of 2 × 2 games thus provides a unifying framework to conveniently locate all 2 × 2 games in payoff space, and aid understanding of relationships between elementary models of strategic situations.

Figure 3. The complete set of 2 × 2 ordinal games. Symmetric games form the diagonal axis in this schematic diagram of an expanded topology of 2 × 2 games that includes games with ties. Games are linked by half-swaps that make or break ties. Games with low and middle ties games are interlaced with strict games in a checkerboard pattern [13].

Figure 3. The complete set of 2 × 2 ordinal games. Symmetric games form the diagonal axis in this schematic diagram of an expanded topology of 2 × 2 games that includes games with ties. Games are linked by half-swaps that make or break ties. Games with low and middle ties games are interlaced with strict games in a checkerboard pattern [13].

3. Discussion

3.1. Identifying Similar Games

The nomenclature aids identifying games that are the same, or ordinally equivalent, but have been discussed under different names. In the case of particularly famous games, this may already be well-understood. For example, most researchers would know that the strategic situation that game theorists usually refer to as Chicken is often discussed by evolutionary biologists as Hawk-Dove. However, there may be less awareness that the game of Snowdrift [21], often presented with algebraic relationships rather than numeric payoffs, is ordinally equivalent to Chicken. The game of Double Hunt is an interesting illustration of interdependence, where neither person can control their own payoff but can control the other’s payoff, which is why Aruka gives it the name Avatamsaka, based on a Buddhist story of such a situation [22,23]. However, he does not seem aware that this is the game that Rapoport, Guyer, and Gordon had earlier listed as game #79, one of the few non-strict games covered by their analysis of previous research (and a case of what they classed as “degenerate” games) [24]. This example illustrates how the same game may be studied under different names, apparently in ignorance of earlier research.

The nomenclature locates games within the map of 2 × 2 games created by the topology of payoff swaps, and so helps to clarify the relationships between games. Several researchers have noted the payoff structure of the interesting Low Dilemma game that lies between Chicken and Prisoner’s Dilemma [9,24], however it does not seem to have an established name. This game illustrates the limitations of dominant strategies as a solution concept, since they would lead to the unsatisfactory result of both getting the worst outcome. However, the Pareto-superior outcome is still vulnerable to temptation to defect. Having a consistent name could facilitate communication, and might be helpful in directing more attention to this and other interesting games. While game theory has tended to concentrate on the most difficult situations, names may also help direct more attention to situations, such as the second-best games of Deadlock and Compromise, which are not as potentially tragic, but which nonetheless may represent empirically important phenomena.

Robinson and Goforth point out that although there has been an enormous amount of research devoted to Prisoner’s Dilemma, many studies have focused on a single version, employing the payoff matrix used by Axelrod [25]. There has been almost no research on the adjoining asymmetric games, which also have Pareto-inferior equilibria. They offer a story where one prisoner has an alibi, creating an asymmetric structure [2]. However, they use the name Alibi for two different ordinal games (Stag Hunt × Dilemma and Assurance × Dilemma). For the third game with a Pareto-inferior equilibrium (Coordination × Dilemma) they use Steven Brams’ name, Revelation (which comes from his analysis of Biblical stories) [7,26]. The nomenclature, based on twelve strict symmetric games and seven types of tie transformations, provides an efficient way to locate similar and different games within the multitude of possibilities.

3.2. Distinguishing Different Games

Conversely, games with differences in ordinal structures that may have significant strategic implications are sometimes referred to with the same name, such as the variety of different stag hunt games that have two Nash Equilibria, one of which is Pareto-inferior. A systematic nomenclature can help distinguish between similar games, disambiguating games that otherwise might be confused. Robinson and Goforth apply one name, Coordination to two of these symmetric games, which this nomenclature distinguishes as Assurance [27] and Coordination. In one case, risk avoidance in a maximin strategy, preventing the worst payoffs, conflicts with achieving the best for both, so there is a severe assurance problem. However, in the other situation, a maximin strategy would also choose the move that leads to the Pareto-superior outcome. In addition to the three symmetric stag hunts, there are also three more pairs of asymmetric strict stag hunts, and many more with ties, which could offer fertile ground for additional study. Understanding the diversity of stag hunts, with a clear way to distinguish between similar but distinct games, could facilitate experimental research and comparison to look at the relationship that different payoff structures have with risk avoidance and maximin strategies. This might also contribute to a deeper understanding of trust and other social dynamics [28].

Some of the asymmetric battle games mix the (4,3/3,4) equilibria of Leader or Hero with the (4,2/2,4) equilibria of Chicken. One of these is the game Buchanan called Passive Samaritan’s Dilemma (Battle × Chicken), (which differs from Active Samaritan’s Dilemma (Harmony × Chicken) by switching the best and second-worst payoffs, equivalent to making two swaps in adjoining payoffs). It is useful to be able to uniquely identify this ordinal game and put it into context with Chicken and its other neighbors. Even the archetypal coordination game, Double Coordination, analogous to the choice of conventions such as which side of the road to drive on, seems to lack an established name. Gintis [29] refers to this as Merchant’s Dilemma, based on a story about silent trade, exchanging offers set out on a beach. The nomenclature provides a way to identify this and other games, including distinguishing among the variety of different games with multiple equilibria.

3.3. Locating Interesting Games

Zero-sum games were a central area of interest in early game theory. However, the only symmetric zero-sum game (more precisely for ordinal games, zero rank-sum) [2], located between Chicken and Deadlock, also seems to lack an established name. The nomenclature provides a standard name to identify the game based on its location, Middle Deadlock, though it might also be called Zero-sum as a common name.

The middle ties game Middle Harmony, located between Harmony and Concord, exemplifies situations where individual incentives lead to the best outcome, without requiring strategic anticipation or coordination, as with Adam Smith’s invisible hand (though it may still be useful to be aware that one is in such a favorable situation, rather than something more difficult or uncertain). The topology also makes clear that while such favorable situations occur, they are far outnumbered by situations where narrow non-strategic behavior does not necessarily lead to win–win.

High Hunt, the game between Prisoner’s Dilemma and Stag Hunt offers another example of an interesting game that seems to have received little attention. High Hunt shares the problems of two kinds of social dilemmas: (weakly) dominant strategies lead to a Pareto-inferior equilibrium, and cautious avoidance of the worst outcome also leads to the inferior equilibrium, so the game shows both a social trap that is a tragedy of collective action [30,31,32] and an assurance problem [27,33].

There are many asymmetric games with ties that may prove interesting, particularly those with payoff structures based on Prisoner’s Dilemma and its close neighbors. Simpson examined the game he called Red Dress (Double Hunt × Low Dilemma), where indifference may create apparently paradoxical incentives [34]. A game with low and middle ties (Middle Hunt × Low Dilemma) can be seen as a payoff structure for a moral hazard, which a swap in high payoffs transforms into a situation with well aligned payoffs for a principal and agent (Middle Hunt × Low Concord). Brams’ Theory of Moves [7] seems to have been motivated in part by the potential for finding better, “non-myopic,” solutions to situations such as those in the game he names based on the Biblical story of Samson and Delilah (Concord × Battle), where a second-best, (3,3) outcome could be preferable to the seemingly unfair (4,2) equilibrium. Brams is one of the few researchers who has paid systematic attention to asymmetric games, one reason that Robinson and Goforth’s periodic table [18] includes many of his names. However, in some cases, Brams gives the same name to several different ordinal games, and so designates a set games, which he calls a generic game [26], (and which may form a connected region in the topology). By providing unique names, the nomenclature could facilitate systematic attention to these and other asymmetric games.

Cyclic games are a particularly interesting group of asymmetric games, and have been used to examine problems such as law enforcement, for example in Inspector–Evader (Hunt × Battle) and similar cyclic situations [35]. The cyclic games pose challenges for solution concepts, since they lack Nash Equilibria in pure strategies (and mixed strategies cannot be meaningfully calculated for ordinal ranks). Even for ratio or real value payoffs, where mixed strategies could be calculated, the advantages of mixed strategies compared to maximin or other solution concepts may be questionable. Examining the cyclic games shows that in five out of the nine pairs of strict ordinal cyclic games, outcomes are available that would be better for both than a mixed strategy, if they could be reached through agreement on a focal point or other solution concept. Maximin solutions only achieve the superior outcome for two of these five cases. Having a map of the relationships between the various cyclic games, and a way to specify different games, could contribute to more systematic analysis of the relevance of various solution concepts in situations with cyclic payoff structures.

3.4. Proportions

To the extent that payoffs occur randomly, games will appear in the proportions shown in the table [34]. Thus, for example, one fourth of games have win–win outcomes. Cyclic games compose 18 out of 144 games, one eighth of the total, as shown in Figure 1. If payoffs are restricted to four values, and ties are allowed, the expected proportions of games differ from those in the table [36]. However, as more values are allowed, then the expected proportions will tend towards those in the 144 games in the topology table [34]. This would also apply to mapping of ordinalized or normalized equivalents onto the topology [37].

Thus, for example, in thinking about the evolution of human cooperation [36], to the extent payoffs occurred randomly, stag hunt games would have occurred about 6.25% of the time (18/144), favoring cooperation with no incentive to defect if coordination could be achieved. By contrast, Prisoner’s Dilemma and other social traps where following a dominant strategy leads to a Pareto-inferior result would have been slightly less common, 4.86% (7/144). Win–win, biased, and second-best games, where cooperation at least gets second-best, are much more frequent, 64% (92/144) than games with equilibria where one or both get poor, second-worst outcomes (Unfair, Traps, and Sad payoff families) or cyclic games which lack Nash Equilibria. More generally, the topology can be seen as a fitness landscape that favors the evolution of cooperation [37].

3.5. Game Names as Coordinates in Payoff Space

In the payoff space of 2 × 2 games, ordinal games are like integers plotted on a number line, identifying discrete locations. For normalized payoffs, equally-spaced ordinal values, such as 1,2,3,4, map onto the center of the square representing each game, while other normalized values move towards the side, until games with ties form the borderlines between different ordinal games. (More precisely, the flat projection of the topology on four layers maps the distance between the second-worst payoff and the adjoining worst and second-best payoffs. The relevant coordinates for mapping normalized games can be shown by calculating the second worst payoff as a proportion or percentage of the distance between the worst and second-best. The distance between second-best and the best and second-worst payoffs would map onto “hyperspace” dimensions of high swaps (3↔4) that link layers. Those cross-layer high swap links would similarly be proportionate to the distance of the second-best payoff between second-worst and best.) The ordinal games are like integer Cartesian coordinates mapping locations in the payoff space of 2 × 2 games. The topology thus provides a continuous map of the payoff space of 2 × 2 games, and the ordinal games can be used as coordinates for locating games within this space.

The 2 × 2 games with normalized payoffs are not limited to separate “quantized” entities, and so differ from the Periodic Table of the Elements. The Periodic Table of the Elements is essentially a spiral, with repeating patterns that lend themselves to presentation in a table that wraps from right to left descending row-by-row, patterns which turn out to be based on the underlying structure of electron shells. By contrast, the topology payoff space maps onto a torus (with 37-holes) [2]. It has a vertical and horizontal arrangement of payoff values, and symmetry on diagonal axes (Villarceau circles) including the axis of symmetric games [2]. The rows and columns provide the basis for the naming scheme presented in this paper.

The topology usefully arranges games according to a variety of relevant properties, including symmetry, and the number of dominant strategies and equilibria, which are relevant to solution concepts. However, research indicates that solution concepts do not necessarily align neatly with the boundaries between ordinal games. In some cases, ratio or real payoff values may have a significant impact on solutions [2,5]. Nevertheless, the topology provides a framework, and a map, for exploring relationships between different games. A systematic set of names for games offers a tool for locating games and exploring the diversity of strategic situations that lie within the payoff space of 2 × 2 games.

4. Experimental Section

This section describes methods involved in developing the nomenclature. Earlier numbering schemes were reviewed and tables prepared that show where earlier game numbers fit in the topology of 2 × 2 games. Conventions were specified for representing ordinal payoff ranks with numbers (1,2,3,4) and orienting rows and columns in payoff matrices according to the location of highest payoffs. Unique names were specified for the symmetric ordinal games, based on the transformations that create different types of ties in strict games. These provide a basis for locating and naming asymmetric games, with some additional specifications for games with ties on the highest two payoffs. Abbreviations create a compact notation, and a potential basis for tags and universal resource identifiers to identify research on similar and related games. A simple procedure locates any 2 × 2 game, including those with ratio and real payoff values, by converting payoffs to standard ordinal values, orienting highest payoffs, and finding symmetric games with the equivalent payoff structures.

4.1. Game Numbers

Rapoport and Guyer [6] clarified the seemingly enormous variety of 2 × 2 games by showing that there were only 78 strategically distinct strict ordinal games, if payoff matrices equivalent by switching row, column, or position are considered to be the same game. They listed the 78 games with numbers (but no names) in an appendix to their book on 2 × 2 games [24]. Their numbers are shown in Figure 4a. For his Theory of Moves and accompanying typology of games, Steven Brams [7] assigned a different set of numbers to strict ordinal 2 × 2 games, shown in Figure 4b. Numbers were not assigned to “no conflict” games, those with win–win outcomes, since they were not of interest for that analysis.

Figure 4. Three schemes for numbering strict ordinal games.

Figure 4. Three schemes for numbering strict ordinal games.

As part of their topology of 2 × 2 games, Robinson and Goforth assigned three-digit index numbers, with the first digit based on the layer, and the second and third on the row and column within the layer, as shown in Figure 4c. In the topology, games related by switching row and column positions of players are treated as different, creating pairs of games reflected around the diagonal axis of symmetry. Thus, numbers are needed for 144 games created by combining 12 different payoff patterns. Twelve of these are strict symmetric games, on the diagonal axis, while there are 66 pairs of asymmetric games, equivalent by switching row or column positions. The 12 symmetric and 66 asymmetric games make up the total of 78 strategically distinct 2 × 2 strict ordinal games, if positions are not considered relevant. If position as Row or Column is important, then 66 reflected pairs of asymmetric games, plus 12 symmetric games, compose a total of 144 strict ordinal games.

Robinson and Goforth chose to start their numbering with the most famous game, Prisoner’s Dilemma, a reasonable but somewhat arbitrary choice. In hindsight, this is comparable to beginning the periodic table of the elements with element 92, Uranium, an element that is interesting, dangerous, and complex. Furthermore, scrolling the layers to display Prisoner’s Dilemma next to the center elegantly arranged games according to their properties, but meant that their index numbers ended up in the sequence 1 6 5 4 3 2, making the numbering scheme unintuitive on first encounter, and somewhat complicated to learn and use.

Consistent with starting with Prisoner’s Dilemma as game 111, Robinson and Goforth put Prisoner’s Dilemma, and its layer of discord games with highest payoffs in diagonally opposite cells, in the lower left part of their table. A more logical arrangement, analogous to Cartesian coordinates that conventionally increase up and to the right, is to put the layer of simpler win–win games in the lower left, and the more complex discordant games in the upper right. If games with no dominant strategies and either two Nash Equilibria (stag hunts and battles) or none (cyclic) are placed in the upper right quadrant of each layer, then there is also a general trend toward increasing complexity within layers.

Binomial names are easier to remember than arbitrary numbers, if the number of names can be kept small. While it might be possible to come up with unique names for all the strict 2 × 2 ordinal names, these would be hard to remember, and impossible for the much larger number of games with ties. Names can be linked with numbers where needed, as shown by the abbreviations in Figure 4. Binomial names are also consistent across different ways of arranging layers and sequencing symmetric games within layers. Robinson–Goforth index numbers can also be extended to games with ties, adding a letter on the beginning to show the preference order (type of ties). The Supplementary Materials for this paper include cards showing each symmetric ordinal game, with names, graphs, and numeric payoff matrices, as well as abbreviations, indices, preference orders, dominant strategies, tile locations (showing hotspots and pipes), externalities, and payoff icons.

4.2. Payoff Values

Ordinal payoffs are defined only by their relative ranks, and may be given in terms of algebraic inequalities, for example a > b > c > d. However, if different authors define the inequalities using different symbols, this makes it harder to recognize games that are similar or ordinally equivalent. For specific ordinal games, it is easier and more intuitive to show simple numeric payoffs. While some authors start with zero, this may be confusing, especially if payoff values are transformed. The nomenclature proposed here follows Rapoport, Guyer, and Gordon [24]; Robinson and Goforth [2]; and many others in showing payoff values with numerals in ordinal ranks from one to four: 1 < 2 < 3 < 4. It should be noted that payoffs expressed algebraically may be equivalent to multiple games and to regions within the topology, which may also be mapped onto the topology.

For showing ties on a 1–4 scale, low ties can be treated as setting the two lowest values to 1 and high ties setting the two highest values to 4. This convention makes it easier to follow the half-swap transformations that form games with ties. Ties for middle payoffs can be conveniently shown as 3, (which takes up less space than 2.5, and since the decimal is not relevant for ordinal ranks). Because the null “game” of complete indifference is unique, it may sometimes be appropriate to show it with zero values for payoffs, all equally good, equally bad, or equally undifferentiated. Following a standard convention for displaying numeric payoff values from one to four makes it easier to identify games that are ordinally equivalent or similar.

4.3. Row and Column Orientation

Interchanging rows or columns or both allows a game to be arranged in as many as four different ways, which are usually considered to be equivalent [24]. The different ways of arranging payoffs are another reason it may be hard to identify and compare games that are the same or ordinally equivalent. Rapoport, Guyer, and Gordon [24] defined a “natural outcome” and put that in the upper left corner (with some exceptions), which makes the arrangement dependent on understanding and applying their criteria for natural outcomes. Robinson and Goforth primarily rely on graphs to display games, an approach that avoids the need for orienting numeric payoffs in rows and columns, since graphs are the same for any of the possible versions of a game obtained by switching rows and columns.

As suggested by Robinson and Goforth [2], it is useful to specify the arrangement of payoffs based on the location of best payoffs and to choose one arrangement as a default. For numeric payoff matrices, they use a convention of putting Row’s highest payoff (4) in the right column, and Column’s highest payoff in the upper row, which can be summarized as: Row’s 4 right, Column’s 4 up, or Right-Up (although they make an exception, not used for this nomenclature, to put 3,3 equilibria in the upper right). They justify this arrangement as being consistent with the convention in Cartesian graphs of putting higher values up and to the right. By contrast, discussions of Prisoner’s Dilemma and other symmetric 2 × 2 games usually place the cooperate-cooperate (CC) outcome in the upper left cell, a Left-Up orientation. However, the concept of a cooperate-cooperate outcome is problematic for battles, and for many asymmetric games, making this questionable as a basis for orienting the arrangement of payoffs.

Subscripts provide a convenient way to identify different orientations of the same game, equivalent by interchanging rows or columns. Thus, Robinson and Goforth’s version of Prisoner’s Dilemma would be Right-Up: Pd_RU while the format used by Axelrod and many others, with the cooperate-cooperate cell in the upper left, would be Left-Up: Pd_LU. The discussion here will follow Robinson and Goforth’s choice of a Right-Up, “Cartesian” display as the default arrangement, which is conveniently consistent with graphical displays of game payoffs. As with using numeric values from one to four, a default arrangement with Row’s highest payoff in the right column and Column’s best payoff in the upper row makes it easier to identify equivalent and similar games.

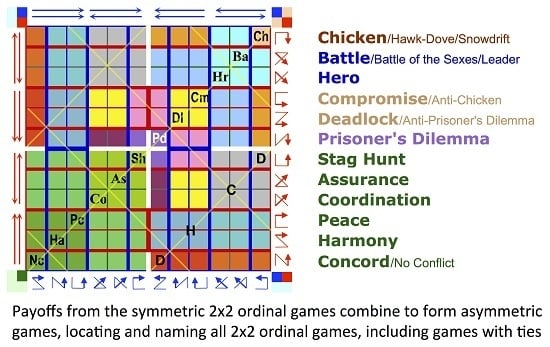
4.4. Strict Symmetric Games

Most but not all of the twelve strict symmetric ordinal games have established names. The nomenclature proposed here tries to follow established names where appropriate, particularly those in Robinson and Goforth’s Periodic Table of 2 × 2 Ordinal Games [18], while also seeking names that are distinctive and that will yield different abbreviations for a compact notation. The discussion starts with the six discordant games on Layer One, where best payoffs are diagonally opposed, including the famous games that have been the subjects of most research in game theory, and then proceeds to the win–win games on Layer Three.

4.4.1. Layer One: Discord Games

Prisoner’s Dilemma. With its combination of dominant strategies leading to a Pareto-inferior Nash Equilibrium, Prisoner’s Dilemma is arguably the most unique strict ordinal symmetric game and already has a well-established name. Where a shorter name is needed for naming games resulting from combining payoffs or transformations creating ties, these may be labeled just using the word dilemma, for example the Low Dilemma game between Prisoner’s Dilemma and Chicken, formed by ties in the lowest two payoffs.

Deadlock. Swaps in middle payoffs turn Prisoner’s Dilemma into the game sometimes called Deadlock [38]. Robinson and Goforth call this game Anti-Prisoner’s Dilemma, based on the similarity in the payoff graph. In this game, following dominant strategies means that neither gets their best payoff, and instead at the Nash Equilibrium both get second-best. For a nomenclature, positive names are preferable to ones that define a game in terms of another game. Avoiding “anti” names also makes for shorter names and more convenient abbreviations, so Deadlock is proposed as the standard name for this game. For naming games with ties, this may be shortened to Lock.

Compromise. Switching lowest payoffs in Deadlock creates another second-best game, which Robinson and Goforth refer to as Anti-Chicken, again based on the similarity in the “wiring diagram” of the payoff graph. The name proposed here is Compromise. This avoids defining the game in terms of another game, abbreviates more distinctly, and also, compared to the name for its neighbor Deadlock, reflects a less grim view of the not-so-bad result where dominant strategies lead both players to get second-best.

Hero. Rapoport [39] distinguishes the two strict battle games as Hero and Leader, based on the payoff to the player moving away from the “natural” maximin outcome when both avoid the worst payoff but instead get second-worst. In Hero, the player who changes to the other move, making it possible to reach a Nash Equilibrium, gets second-best as a result, making a kind of heroic sacrifice.

Battle. In Leader, the one who moves from the maximin outcome of both getting second-worst gets the best payoff, while the other gets second-best. Robinson and Goforth use the original name, Battle of the Sexes [40], for this game. Concern about gender stereotypes has led to suggestions for alternative names, such as Bach or Stravinsky, (allowing the same abbreviation, BoS) [41]. A more accurate name, capturing the conflict over first preferences (while avoiding gender stereotypes) might be Battle of Favorites. The name Battle is proposed here, for simplicity and shortness, to reduce concerns about sexism or gender stereotyping, and because the initial “B” provides a more distinctive abbreviation than the letter “L.” Alternative common names for this game would then include Leader, Battle of Favorites, Battle of the Sexes, and Bach or Stravinsky. As with scientific names for species in Linnaean taxonomy, it may be convenient to follow the common name with the binomial name in parentheses, in italic font, for example: Leader (Battle).

Chicken. The second-most famous game has two Nash Equilibria, both with unequal payoffs, where one or the other gets their best result while the other gets second-worst. Both are tempted to defect from the cooperative second-best outcome that would result if both play a dove strategy. However, if both try to get their best result, pursuing a Hawk strategy, they instead both end up at the worst outcome.

4.4.2. Layer Three: Win–Win Games

Stag Hunt. Swapping the top two payoffs for both players turns Prisoner’s Dilemma into Stag Hunt. For the strict ordinal game where the inferior equilibrium is second worst, Robinson and Goforth’s name seems well-suited, reflecting Rousseau’s story [42] about the hunter preferring the safer but much less desirable choice of a rabbit rather than a share of a stag that might be gained if others could be trusted to cooperate.

Assurance. Robinson and Goforth labeled both the other two symmetric ordinal stag hunts as Coordination. However, for the nomenclature there is a need to distinguish between them. The game next to Stag Hunt, resulting from swapping middle payoffs, represents a more severe form of an assurance problem as defined by Sen [27]. This occurs where there are two equilibria, one Pareto-inferior, and if the other does not choose the move that would lead to the best equilibrium, then it is better to also choose the alternate move. Thus, the assurance problem poses a conflict between getting the best, win–win outcome if the other can be trusted to cooperate, and doing much worse if the other does not choose to cooperate.

Coordination. In the third of the three strict symmetric stag hunts, the move that avoids the worst payoff also makes it possible to achieve the best, as discussed earlier. While there is an assurance problem, it is milder, since a player will not get the worst outcome, regardless of what the other does. It may be noted that the term coordination game can also be used in a more general sense. Some games require coordination to choose between one of two equilibria, including not only the strict win–win games of Stag Hunt, Assurance, and Coordination, but also Hero, Battle, and Chicken. This also applies to simpler games with ties, such as the simplest coordination game (Double Coordination) discussed below. In a looser sense, the term coordination could also include some cyclic games. In these games, players may seek a way to coordinate on the choice of a desirable outcome, perhaps through choosing a prominent focal point [12]. The more general meaning of the term coordination games is a reason to prefer the term stag hunts to identify the games with two Nash Equilibria, one win-win and one Pareto-inferior, and since the term stag hunt seems to be more commonly used than assurance.

Peace. This was the only one of the twelve strict symmetric games originally left nameless by Robinson and Goforth. [2] It is a game of mixed motives or mixed interests [2,12]. Its symmetric neighbors, Coordination and Harmony, are games of pure cooperation where one player’s incentives always lead to moves that also raise the other player’s payoff, all positive externalities and, in Greenberg’s [11] terminology, positive inducement correspondences. In Peace, there is an underlying conflict, a negative inducement correspondence, which is avoided. As long as the other player follows the logic of a dominant strategy and chooses the move that includes win–win, the first player’s incentives lead to a move that raises payoffs for both, a positive externality. However, if the other player did choose the alternate move, which does not lead to win–win, then the first player’s incentives would encourage a move that would make things worse for the other, imposing a negative externality. Thus in this situation, there is a degree of underlying conflict, even if dominant strategies mean that incentives should lead both to the win–win outcome, suggesting Peace as an appropriate name, for a situation where a potential conflict has been overcome.

Harmony. Incentives are strongly aligned in Harmony, where moves following dominant strategies raise payoffs by two ranks, from worst to second-best or second-worst to best. Robinson and Goforth do not cite a source for this name, but it seems appropriate.

Concord. Moves following dominant strategies only raise payoffs by one rank, but still lead both to win–win, so the incentives are in the same direction as Harmony, although not as strong. Robinson and Goforth originally called this game No Conflict. However, for games with ties (discussed below), names based on the tie transformations would lead to awkward terminology, such as Low No Conflict or High No Conflict. Therefore, the name Concord, with a similar meaning, is proposed, which conveniently also allows Nc and N as workable abbreviations. Using the letter N helps to distinguish this from Coordination, Compromise, and Chicken, which also begin with the letter C.

In a later publication, Robinson and Goforth [5] used the names Boring, Anti-Boring, and Anti-Stag Hunt, for Concord, Harmony, and Peace, which could be treated as alternative common names. It may be noted that all the games with win-win payoffs are sometimes called “no-conflict” games [7,24]. However, this is inaccurate if it includes the stag hunts, which are a kind of social dilemma where in some cases achieving the mutually best outcome conflicts with risk minimization, if assurance that others will cooperate is problematic. Therefore, win–win seems a more suitable appellation. Robinson and Goforth’s Layer numbers may also be used for simplicity, with the win–win games designated as Layer 3.

4.5. Symmetric Games with Ties

Games with ties can be linked by half-swaps that make or break ties, expanding the topology and providing a natural ordering for the complete set of 2 × 2 ordinal games. Thus, games with ties lie between the strict ordinal games [13,14,15]. For a nomenclature, symmetric games with ties can be identified as transformations from the twelve strict symmetric games. In the other direction, starting from the null game of complete indifference, breaking ties differentiates payoff structures into games with three ties for high or low payoffs, and then with two ties, or only a pair of ties for one or both players, followed by strict games. Combinations of the eight preference orderings divide 2 × 2 ordinal games into 64 preference classes, as shown in Figure 5. A nomenclature based on the symmetric ordinal games requires coming up with distinctive names for all the symmetric ordinal games, (as discussed above) and specifying distinctive names for the types of ties and the resulting games.

Low Ties. These games usually form ideal types for the neighboring strict games. Assigning names based on the adjoining strict games requires a choice, sometimes somewhat arbitrary, between the two neighbors. In general, the approach here favors the “lower left” game in the respective tile, the one nearer to Harmony. However, applying this rule too rigidly would sometimes generate misnomers, inaccurate names, such as Middle Dilemma, rather than Middle Deadlock, which actually has a single, second-best, equilibrium, like Deadlock. Therefore, to obtain more meaningful names, a slightly more flexible approach is applied. Low Battle lies between Hero and Leader (Battle), Low Lock between Deadlock and Compromise, Low Coordination between Assurance and Coordination, and Low Harmony between Harmony and Peace. Low Concord lies between Concord and Stag Hunt. Since it has weakly dominant strategies leading to a single win–win Nash Equilibrium, it is not a stag hunt and so is more like Concord. In Low Dilemma between Prisoner’s Dilemma and Chicken, weakly dominant strategies would lead to a Pareto-inferior outcome at a single equilibrium where both get the worst payoff, an unsatisfactory outcome.

Figure 5. Types of ties categorize the complete set of 2 × 2 ordinal games into eight preference orderings and sixty-four preference classes. Adapted from [13]. For preference orderings A–H see [9,10].

Figure 5. Types of ties categorize the complete set of 2 × 2 ordinal games into eight preference orderings and sixty-four preference classes. Adapted from [13]. For preference orderings A–H see [9,10].

Middle Ties. Volunteer’s Dilemma (Middle Battle) [43,44] is the most well-known game with ties for middle payoffs, and (along with Matching Pennies) is one of the few games with ties to have been the subject of substantial research and to have an established name. Volunteer’s Dilemma can be formed by making ties for middle values in Chicken or Battle. Middle Compromise is a second best game, between Hero and Compromise. Middle Deadlock, between Deadlock and Prisoner’s Dilemma, also has a second-best equilibrium. Middle Deadlock is remarkable as the only symmetrical zero-sum game (or more precisely, zero rank-sum ordinal game), and so an ideal type or exemplar of zero-sum games, although its uniqueness does not seem to have been recognized. Middle Hunt lies between Stag Hunt and Assurance. The usual story of Rousseau’s Stag Hunt makes no mention of concern about whether or not the other hunter might also safely get a hare, suggesting indifference, in which case a game with middle ties would most accurately model the story, suggesting Rousseau’s Hunt as a common name. Middle Peace is another harmonious game where dominant strategies lead to win–win. This is also the case for Middle Harmony, between Harmony and Concord.

High Ties. High Hunt lies between Stag Hunt and Prisoner’s Dilemma. The symmetric high ties games may come in two versions, depending on the starting point for the tie transformation. High Hunt ends up with the identical arrangement of payoffs as High Dilemma. High Chicken and High Concord also have identical payoff patterns. However, the other high ties games have two alternate variants, which differ by the orientation of rows and columns. One can be designated as the default version, and it seems suitable to prefer the version on Layer Three as a default. Where necessary for locating and naming asymmetric games, preference may also be given to lower left games within a tile, and to games with High Hunt payoffs for games on Layers 2 and 4. For the complete set of 2 × 2 ordinal games, as shown in Figure 3, the alternate variant (shaded gray) of some symmetric games with ties is still needed to form some asymmetric games with ties, including Matching Pennies (Double Coordination × Double Hero, DoDe). High Coordination (and High Assurance) and High Hero (and High Battle) both have two Nash Equilibria, in one of which both get the best payoff. High Concord (and High Chicken), High Harmony (and High Compromise), and High Peace (and High Lock) all have two dominant strategies leading to win–win at a single equilibrium.

Double Ties. These games have ties for both the two highest and two lowest payoffs. The Double Ties symmetric games can also come in alternate versions, equivalent by interchanging rows and columns, and the Layer Three versions can be used as default versions. Although thorough discussion is beyond the scope of this paper, it may be noted that these games are the roots of the two kinds of high swap (3↔4) linkages across layers between equivalently-located tiles identified by Robinson and Goforth, forming “pipes” composed of quartets of tiles and “hotspots” of pairs of tiles. Breaking ties in Double Ties games differentiates them into the six different kinds of hotspots and pipes (pipes are named here according to the combinations of H, C, and D bands; and hotspots by the layers they link).

Triple Ties. In these games, each dislikes one outcome. In both Triple Harmony and Triple Lock, weakly dominant strategies lead to a win–win equilibrium. Triple Lock has a second Nash equilibrium, while Triple Harmony has two more.

Basic Ties. These games are simplified ideal types for Layers One and Three, with best payoffs harmoniously located in the same cell in Basic Harmony, as in Layer Three; and discordantly aligned in diagonally opposed cells in Basic Discord (where synchronizing to take turns could be a solution in repeated play).

Zero. All ties, complete indifference, characterizes the null game where players have no preferences between different outcomes. While normalized versions of all other 2 × 2 games may be mapped onto to the surface of the topology of 2 × 2 games, normalizing the zero game would require dividing by zero. Thus, the Zero Game stays separate from the payoff space mapped by the topology of payoff swaps, like a singularity. It may be seen as the origin at the center of the eight–dimensional payoff space of 2 × 2 games.

Robinson and Goforth showed that the topology of 2 × 2 ordinal games is a torus with 37 holes [2] while the total of 37 strict symmetric 2 × 2 games arises from the number of nodes, edges, and faces in the topology of strict symmetric games, when games equivalent by row and column swaps are only counted once [4,5]. I suggest the conjecture that the number of 37 holes in the topology torus, and 37 symmetric ordinal games, not including the zero game, is not a coincidence regarding the prime number 37, but instead a necessary characteristic of the structure of the topology.

In total, including the zero game, there are 38 strategically unique 2 × 2 symmetric ordinal games. High ties and double ties games have alternate variants, equivalent by interchanging rows or columns, some of which are needed to generate asymmetric games outside Layer 3, so Figure 2 and Figure 3 show 47 symmetric games, including the nine alternates and the zero game.

4.6. Asymmetric Games

As discussed earlier, asymmetric games come in reflected pairs equivalent by switching row and column positions of the players. For convenience, these can be labeled as right-hand forms, below the diagonal line of symmetric games, and left-hand forms, above the diagonal. These are chiral forms with left and right-handed versions (as with chiral molecules that have different isomers). Where position does not matter, the right-hand form could be considered the default exemplar. (For cyclic games with counterclockwise movement, this conveniently happens to follow the “right hand rule” common in science and engineering.)

An advantage of the binomial nomenclature is that it makes the reflected pairs of asymmetric games obvious. By contrast, the Rapoport–Guyer taxonomy and Brams typology do not distinguish between reflections and do not provide a way to identify which is being shown. Robinson–Goforth index numbers do show the two reflections resulting from switching position of row and column. However, the index numbers require understanding the structure of layers and arrangement of games in each layer before it is possible to recognize the reflected variants.

4.7. Abbreviations and Tags

Two-letter abbreviations provide a convenient way to refer to games, following the example of abbreviations for chemical elements. The twelve strict symmetric games can each have their own two-letter abbreviation, for the strict game, and a shorter single letter abbreviation used in designating the related games formed by ties. Names for the types of ties, the different Fraser–Kilgour preference orderings, have been chosen to have different initial letters. Thus, games with ties can be identified with a first letter based on the type of tie, and the second letter based on a strict game from which it is created by a forming a tie. Asymmetric games would have a four-letter abbreviation.

Examples of abbreviations would be as follows:

• Pd: Prisoner’s Dilemma;
• HaCh: Harmony and Chicken, common name: Samaritan’s Dilemma;
• Ld: Low Dilemma;
• DoDe: Double Coordination × Double Hero, common name: Matching Pennies (right-hand, counter-clockwise version.

Abbreviations would be as shown in Table 1. Abbreviations could also be used as online “tags” for games, making it easier to label and find studies of the same game, even when these use different payoff values and orientations. These could be simple hashtags, such as #2×2pd for Prisoner’s Dilemma, which could be used like keywords to label articles and other items dealing with particular ordinal games. The topology of 2 × 2 games can satisfy the requirements of an ontology (in the information science sense of the term) and so could provide unique Universal Resource Identifiers (URIs) for the semantic web [20]. As discussed, a systematic way of identifying a preferred default version for games with high, double, or all ties for one or both players is necessary to locate names, and so provides a basis for unique URIs for all the 2 × 2 ordinal games.

Table 1. Abbreviations provide a compact notation for 2 × 2 Games.

Strict Games
Ch	c	Chicken/Hawk-Dove/Snowdrift
Ba	b	Battle/Leader
Hr	e	Hero
Dl	k	Deadlock/Lock/Anti-Prisoner’s Dilemma
Cm	m	Compromise/Anti-Chicken
Pd	d	Prisoner’s Dilemma
Hu	u	Stag Hunt
As	a	Assurance
Co	o	Coordination
Pc	p	Peace
Ha	h	Harmony
Nc	n	Concord/No Conflict
Types of Ties (Preference Orderings)
1,2,3,4	S	Strict
1,1,3,4	L	Low
1,3,3,4	M	Middle
1,2,4,4	H	High
1,1,4,4	D	Double
1,4,4,4	T	Triple
1,1,1,4	B	Basic
0,0,0,0	Z	Zero/All ties

Table 1. Abbreviations provide a compact notation for 2 × 2 Games.

Strict Games
Ch	c	Chicken/Hawk-Dove/Snowdrift
Ba	b	Battle/Leader
Hr	e	Hero
Dl	k	Deadlock/Lock/Anti-Prisoner’s Dilemma
Cm	m	Compromise/Anti-Chicken
Pd	d	Prisoner’s Dilemma
Hu	u	Stag Hunt
As	a	Assurance
Co	o	Coordination
Pc	p	Peace
Ha	h	Harmony
Nc	n	Concord/No Conflict
Types of Ties (Preference Orderings)
1,2,3,4	S	Strict
1,1,3,4	L	Low
1,3,3,4	M	Middle
1,2,4,4	H	High
1,1,4,4	D	Double
1,4,4,4	T	Triple
1,1,1,4	B	Basic
0,0,0,0	Z	Zero/All ties

4.8. Finding a Game

Starting with a matrix of payoff values, Figure 2 and Figure 5 can be used to find the name, based on the following steps:

• Make ordinal: Rank payoffs as integers from 1 to 4. In case of ties, low ties are 1, high ties are 4, and middle ties are 3.
• Orient Right-Up. Put Row’s best payoff in the right-hand column, and Column’s best payoff in the upper row.
• Categorize by type of ties: Determine the preference ordering for each player’s payoffs.
• Inspect preference class: Within class(es) formed by the preference ordering(s), find the symmetric game with the same payoff pattern by inspection of Figure 2.
• Check for alternate versions: For high ties, double ties, and all ties, check alternate versions formed by interchanging rows and columns to identify the preferred, default, variant as shown in Figure 3. As discussed above, Layer 3 variants, with win–win outcomes in the upper right corner of the payoff matrix, are preferred where available. For high ties, prefer games formed by payoffs from High Coordination, High Hero, and High Hunt. For double ties, prefer games formed by payoffs from Double Hunt, and prefer the right-hand (counter-clockwise) versions, to the right and below the axis of symmetry, such as the right-hand version of Matching Pennies (Double Coordination × Double Hero).

5. Conclusions

Robinson and Goforth’s topology of payoff swaps reveals an elegant structure in the payoff space of 2 × 2 games, which can be mapped onto a flat four-layer display. Names for games based on symmetric games provide coordinates for locating 2 × 2 ordinal games within this payoff space. This paper provides an enhanced visualization of the topology of 2 × 2 games; presents the full set of 38 strategically distinct symmetric 2 × 2 ordinal games, which lie on an axis of symmetry in the payoff space; and proposes an efficient nomenclature for naming and locating any 2 × 2 ordinal game. This nomenclature is based on the topology of swaps in 2 × 2 games, names for the symmetric games, and transformations that create different types of ties. It clarifies the unified order underlying the multitude of 2 × 2 games and different ways of presenting payoff values. It provides names based on the natural order revealed by the topology of 2 × 2 games. The nomenclature provides a consistent and systematic way of identifying all ordinally-equivalent 2 × 2 games and showing their relationships in payoff space. The nomenclature could contribute to clearer communication about games, aid understanding of similarities and differences between various strategic situations of conflict and cooperation, and facilitate cumulative and comparative research in game theory.