Estimating the Product Inhibition Constant from Enzyme Kinetic Equations Using the Direct Linear Plot Method in One-Stage Treatment

Abstract

A direct linear plot was applied to estimate kinetic constants using the product’s competitive inhibition equation. The challenge consisted of estimating three kinetic constants, V_max, K_m, and K_p, using two independent variables, substrates, and product concentrations, in just one stage of mathematical treatment. The method consisted of combining three initial reaction rate data and avoiding the use of the same three product concentrations (otherwise, this would result in a mathematical indetermination). The direct linear plot method was highly superior to the least-squares method in terms of accuracy and robustness, even under the addition of error. The direct linear plot method is a reliable and robust method that can be applied to estimate K_p in inhibition studies in pharmaceutical and biotechnological areas.

1. Introduction

The direct linear plot (DLP) is a graphic method to estimate kinetic constants from enzymatic reactions based on the median as a statistic. The method was developed by Eisenthal and Cornish-Bowden in 1974 [1]. The accuracy and robustness of this method were tested during the estimation of V_max and K_m from the Michaelis–Menten equation [1,2]. As in this article, all of the recent studies regarding the application of DLP are based on the estimation of these two parameters from the Michaelis–Menten equation. The application of DLP to equations with more than two parameters has not been studied until now [3]. This median-based method was applied herein to estimate three kinetic constants from the substrate-uncompetitive inhibition equation. The results indicated that DLP was not only applicable to equations with more than two parameters, but it was reliable and robust when compared to the least-squares (LS) method. In the present article, we explored the application of DLP to the product-competitive inhibition equation, which is a different type of problem, as will be exposed. Some attempts to estimate inhibition constants from enzyme kinetics using DLP have involved estimating apparent kinetic constants and using secondary plots to estimate the values of these inhibition constants. The application of DLP to estimate inhibition constants was first proposed by Eisenthal and Cornish-Bowden [1]. The literature contains outdated examples of this application because the use of DLP to estimate inhibition constants in one-stage has not been assessed [4,5,6,7,8]. In the literature, DLP has been used to estimate the apparent kinetic constants V_max and K_m; however, studies have used secondary plots to estimate the inhibition constant K_p. The present article studied the application of DLP to estimate the product inhibition constant in one-stage treatment, avoiding the estimation of apparent kinetic constants and secondary plots. As the proper characterization of inhibition in pharmaceutical and biotechnological applications is a major concern, the importance of this proposal is that it opens up the possibility of using a reliable and robust method to estimate product inhibition constants. The purpose of this study is to estimate V_max, K_m, and K_p from the competitive inhibition equation in just one stage of calculations, avoiding the apparent constants and secondary plots. This means the values of the product inhibition constants must be obtained from the DLP method, which has never been tried before. The problem is outlined as follows.

The equation for competitive product inhibition involves three parameters—V_max, K_m, and K_p—and three variables—substrate concentration, product concentration, and initial reaction rate (Equation (1)).

$$v=\frac{V_{max}S}{K_m+S+\frac{K_m}{K_p}P}$$

(1)

This is a different type of problem compared to previous articles where the substrate-uncompetitive inhibition equation involved three parameters—V_max, K_m, and K_S—but only two variables—substrate concentration and initial reaction rate (Equation (2)) [3].

$$v=\frac{V_{max}S}{K_m+S+\frac{S^2}{K_s}}$$

(2)

The experimental dataset required is traditionally used in the initial reaction rate method, which denotes a series of initial rates vs. substrate concentrations at constant product concentrations, as indicated in the scheme of Figure 1.

Equation (1) can be rearranged to Equation (3) in the following form:

$$v_{ij}{K}_m-S_j{V}_{max}+\frac{v_{ij}{P}_i{K}_m}{K_p}=-v_{ij}{S}_j$$

(3)

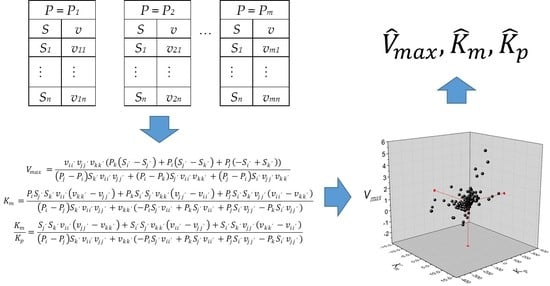
The definition of v_ij is the rate of product concentration P_i and substrate concentration S_j. As the estimation of three parameters is required, three data pairs and three equations are needed to solve the matrix system in Equation (4).

$$\left(\begin{array}{ccc}{v}_{i{i}^{\prime }}& -S_{i^{\prime }}& v_{i{i}^{\prime }}{P}_i\\ v_{j{j}^{\prime }}& -S_{j^{\prime }}& v_{j{j}^{\prime }}{P}_j\\ v_{k{k}^{\prime }}& -S_{k^{\prime }}& v_{k{k}^{\prime }}{P}_k\end{array}\right)\left(\begin{array}{c}{K}_m\\ V_{max}\\ \frac{K_m}{K_p}\end{array}\right)=\left(\begin{array}{c}-v_{i{i}^{\prime }}{S}_{i^{\prime }}\\ -v_{j{j}^{\prime }}{S}_{j^{\prime }}\\ -v_{k{k}^{\prime }}{S}_{k^{\prime }}\end{array}\right)$$

(4)

Likewise, the definition of v_ii’ = v(P_i, S_i’), i.e., i values are between 1 and m (the number of product concentrations), and i’ values are between 1 and n (the number of substrate concentrations). Alternatively, the solution for Equation (4) is presented in Equation (5) in algebraic form.

$$\begin{array}{c}{V}_{max}=\frac{v_{i{i}^{\prime }}{v}_{j{j}^{\prime }}{v}_{k{k}^{\prime }}\left(P_k\left(S_{i^{\prime }}-S_{j^{\prime }}\right)+P_i\left(S_{j^{\prime }}-S_{k^{\prime }}\right)+P_j\left(-S_{i^{\prime }}+S_{k^{\prime }}\right)\right)}{\left(P_j-P_i\right)S_{k^{\prime }}{v}_{i{i}^{\prime }}{v}_{j{j}^{\prime }}+\left(P_i-P_k\right)S_{j^{\prime }}{v}_{i{i}^{\prime }}{v}_{k{k}^{\prime }}+\left(P_j-P_i\right)S_{i^{\prime }}{v}_{j{j}^{\prime }}{v}_{k{k}^{\prime }}}\\ K_m=\frac{P_i{S}_{j^{\prime }}{S}_{k^{\prime }}{v}_{i{i}^{\prime }}(v_{k{k}^{\prime }}-v_{j{j}^{\prime }})+P_k{S}_{i^{\prime }}{S}_{j^{\prime }}{v}_{k{k}^{\prime }}\left(v_{j{j}^{\prime }}-v_{i{i}^{\prime }}\right)+P_j{S}_{i^{\prime }}{S}_{k^{\prime }}{v}_{j{j}^{\prime }}(v_{i{i}^{\prime }}-v_{k{k}^{\prime }})}{(P_i-P_j)S_{k^{\prime }}{v}_{i{i}^{\prime }}{v}_{j{j}^{\prime }}+v_{k{k}^{\prime }}(-P_i{S}_{j^{\prime }}{v}_{i{i}^{\prime }}+P_k{S}_{j^{\prime }}{v}_{i{i}^{\prime }}+P_j{S}_{i^{\prime }}{v}_{j{j}^{\prime }}-P_k{S}_{i^{\prime }}{v}_{j{j}^{\prime }})}\\ \frac{K_m}{K_p}=\frac{S_{j^{\prime }}{S}_{k^{\prime }}{v}_{i{i}^{\prime }}(v_{j{j}^{\prime }}-v_{k{k}^{\prime }})+S_{i^{\prime }}{S}_{j^{\prime }}{v}_{k{k}^{\prime }}\left(v_{i{i}^{\prime }}-v_{j{j}^{\prime }}\right)+S_{i^{\prime }}{S}_{k^{\prime }}{v}_{j{j}^{\prime }}\left(v_{k{k}^{\prime }}-v_{i{i}^{\prime }}\right)}{\left(P_i-P_j\right)S_{k^{\prime }}{v}_{i{i}^{\prime }}{v}_{j{j}^{\prime }}+v_{k{k}^{\prime }}(-P_i{S}_{j^{\prime }}{v}_{i{i}^{\prime }}+P_k{S}_{j^{\prime }}{v}_{i{i}^{\prime }}+P_j{S}_{i^{\prime }}{v}_{j{j}^{\prime }}-P_k{S}_{i^{\prime }}{v}_{j{j}^{\prime }})}\end{array}$$

(5)

The rank of the matrix in Equation (4) must be 3 for the system to have a solution. For the case when three product concentrations are taken from the same set, P_i = P_j = P_k, the system has no solution because the rank of the resulting matrix is 2. This problem can be easily checked by observing the denominators of Equation (5) when replacing P_i, P_j, and P_k with the same value of product concentration. The strategy proposed to solve this system is to take at least two different values of product concentration. In this way, the total number of feasible data combinations will be calculated using Equation (6).

In consequence, calculations of the kinetic constants V_max, K_m, and K_p will be obtained from the combination of two P values from the same dataset, one P from a different one, and the combination of three different P values from three datasets. A list of V_max, K_m, and K_p values from the total combinations indicated in Equation (6) will be obtained. Finally, the estimators of V_max, K_m, and K_p correspond to the median values from the list.

$$\left(\begin{array}{c}m·n\\ 3\end{array}\right)-\left(\begin{array}{c}n\\ 3\end{array}\right)·m$$

(6)

This article aims to compare the quality of the kinetic constant estimations from the product inhibition equation between the DLP and the LS methods.

2. Results and Discussion

As in our previous article [3], this problem consists of estimating three kinetic constants, but in this new case, three experimental variables will be used. Experimental data of initial rate perturbed with a random error of variance σ² were simulated in a dataset of 1000 runs. The dataset, according to

Table 1. Experimental design of substrate and product concentrations to calculate initial reaction rates.

P1 = 0		P2 = 0.5Kp		P3 = Kp		P4 = 2Kp		P5 = 4Kp
S	v	S	v	S	v	S	v	S	v
0.1	v11	0.1	v21	0.1	v31	0.1	v41	0.1	v51
0.2	v12	0.2	v22	0.2	v32	0.2	v42	0.2	v52
0.5	v13	0.5	v23	0.5	v33	0.5	v43	0.5	v53
1.0	v14	1.0	v24	1.0	v34	1.0	v44	1.0	v54
2.0	v15	2.0	v25	2.0	v35	2.0	v45	2.0	v55
5.0	v16	5.0	v26	5.0	v36	5.0	v46	5.0	v56
10.0	v17	10.0	v27	10.0	v37	10.0	v47	10.0	v57

, considers the values of the kinetic constants 1, 1 and 10 for V_max, K_m, and K_p, respectively, and the initial rates vs. the substrate concentrations at different product concentrations were plotted in Figure 2.

These data were used to estimate the kinetic constants using the DLP and LS methods. An example of the dataset obtained for the values of the kinetic constants V_max, K_m, and K_p with a normal distribution of error and variance 0.01 is plotted in Figure 3.

The number of kinetic constant values plotted in Figure 3 and Figure 4 was 6370. This amount of data was obtained avoiding the use of the same three product concentrations during the calculations with Equation (4). The dispersion of the data was enormous compared to the value of the kinetic constant, as can be observed in Figure 4. This is a typical result of the application of the DLP method to the estimation of kinetic constants. This behavior can be observed in previous publications [1,3,9]. Many points were left out of the layers just for illustration purposes; however, the vast majority of data are inside of layers corresponding to 98%, 99% and 99% for V_max, K_m and K_p, respectively. In terms of dispersion, 56% of calculated V_max values are in the range 0.95–1.05; 22% of calculated Km values are in the range 0.95–1.05 and 24% of calculated K_p values are in the range 9.5–10.5. The amount of data plotted in Figure 3 and Figure 4 was obtained to estimate the kinetic constants V_max, K_m, and K_p by calculating the median for each of them. This is the procedure needed in routine experiments to determine the inhibition constant K_p. The statistical evaluation of DLP requires the repetition of this procedure to avoid bias and erroneous conclusions. A total of 1000 experimental runs were carried out to evaluate and compare the quality of the estimations between the DLP and the LS methods. A comparison of the lower values of the sum of squared residuals (SSR) between DLP and LS is plotted in Figure 5. The DLP method obtained lower values of SSR for all the values of variance in the range from 0.001 to 0.020 when both procedures—calculation of the median of K_m/K_p and the median of K_p—were carried out. The calculation of the median of K_m/K_p was slightly superior for almost all variances explored. For example, at variance 0.010, the calculation of the median of K_m/K_p obtained a frequency of 0.8 compared to 0.78 for calculation of the median of K_p. This was not significant to conclude that one procedure was better than the other. However, when both calculations were compared regarding the SSR between them, the result depended on the variance, as shown in Figure 6a. The calculation of the median of K_m/K_p obtained a lower SSR at variance values lower than 0.010. The calculation of the median of K_p offered lower values of SSR at variances higher than 0.010. The effect of the ratio K_p/K_m was slightly superior to the calculation of the median of K_p, as shown in Figure 6b. However, this was not significantly different. In consequence, which procedure is better, in terms of the SSR, depends on the experimental error.

The relative error of the estimated kinetic constants by LS and DLP methods was plotted for 1000 experimental runs in Figure 7. The DLP always resulted in a lower accumulation of relative error during estimations of the three kinetic constants. The product inhibition constant K_p accumulated the highest relative error when estimated by both LS and DLP methods. However, the accumulated relative error was less than half with DLP compared to LS. This result shows that DLP is a very accurate method to estimate the competitive inhibition constant. The product inhibition constant K_p estimated with DLP method accumulated a lower relative error than the LS method even at higher variance σ² (experimental error), as shown in Figure 8. The behavior patterns of both the median of K_m/K_p and the median of K_p were repeated. The median of K_m/K_p was slightly more accurate at variances lower than 0.010. At higher values, the median of K_p was more accurate.

The effect of outliers was analyzed by adding fixed error values to the initial rate v₃₄ (S = 1; P = 10). The added error ranged from −0.01 to +0.01. The results are shown in Figure 9. The estimated values of V_max by LS were constant due to an artifact of the estimation method. The estimated V_max was obtained by choosing the highest value from the five non-linear regressions corresponding to the five datasets of product concentrations. The error was added to the initial rate value corresponding to the third dataset of product concentration; in consequence, the highest value of V_max was not perturbed, and it was always the same value. The DLP method estimated K_m and the K_p with more accuracy and with less perturbation than the LS method. Although the LS method estimated K_p with more accuracy at some high positive values of fixed error, the results clearly showed that DLP was more robust than the LS method. The perturbation generated by the added error is plotted in Figure 10. The perturbation of Vmax was omitted due to the artifact during its estimation by the LS method. The results indicated that the estimation of kinetic constants K_m and K_p was much less perturbed when the DLP method was used. Almost all the perturbations were maintained below 1%, compared to the LS method, where perturbations were in the range from 4% to 8%.

The DLP method exhibited the same pattern of behavior than that observed during application to the uncompetitive inhibition equation [3]. Lower SSR and estimation errors compared to the LS method were observed during estimations of the competitive inhibition constant. Again, the DLP method demonstrated accuracy and robustness during the estimation of kinetic constants. The possibility of using the DLP method to estimate inhibition constants in pharmaceutical and biotechnological studies was demonstrated. The performance of the DLP method applied to the competitive inhibition equation was different compared to the application of the substrate-uncompetitive inhibition equation previously studied. The addition of a variable product concentration caused mathematical indetermination during the calculations. The problem was overcome by avoiding using the same three product concentrations in Equations (4) and (5). This obligated a reduction in the number of combinations from 6545 to 6370, where 175 combinations resulted in the indetermination of the matrix (Equation (4)). Another difference is the dependence of K_p on the value of K_m, which can be observed in Equation (5), where the calculation consisted of the K_m/K_p value, and K_p was calculated after obtaining K_m. A significant implication of this is the transmission of the K_m error to K_p. Interestingly, based on the observations, this effect was not important. In general, the estimation of K_p by DLP was more accurate and robust than estimation by the LS method. The application of DLP to the uncompetitive inhibition equation exhibited a higher accuracy just in some cases compared to the LS method. In terms of robustness, the DLP was highly superior to the LS method. Presently, in this study, a higher superiority in terms of accuracy and robustness was observed. Despite the higher complexity of the competitive inhibition equation, requiring one more independent variable than the substrate-uncompetitive inhibition equation, the results were better. The transmission of error from K_m to K_p could be the key. This error is surely amplified when transmitted from one constant to another, and based on the observations, the effect was better softened by DLP compared to the LS method.

As Cornish-Bowden and Endrenyi commented [10], the median method cannot readily be generalized to equations of more than two parameters. This sentence became true when we found a mathematical issue during the application of the DLP to the product’s inhibition equation, where an indeterminate system of equations (Equation (5)) is generated when the same value for the product concentration was used. However, this problem can be solved by selecting the proper combination of data. We, again, demonstrated that DLP can be applied to equations with more than two parameters. Presently, we also demonstrated the application to equations with more than two variables.

We conclude that the DLP method is better than the LS method to estimate the product’s competitive inhibition constant in terms of accuracy and robustness. We now count on a new tool to estimate the product-competitive inhibition constant with reliable results.

3. Method

3.1. Experimental Design

The set of substrate and product concentrations was designed by first setting the real values of kinetic constants V_max, K_m, and K_p. The chosen values were 1 for V_max and K_m, and five different K_p values, including 10, 20, 50, 100 and 200, to study the effect on the estimation of the kinetic constants. These values correspond to the dimensionless kinetic constants in the case of V_max and K_m. Dimensionless V_max is the limit of S/(S + K_m) when S tends to infinity. Dimensionless K_m is obtained when the kinetic equation is written in the form S/K_m/(S/K_m + 1). In the case of K_p, the dimensionless value corresponds to K_p/K_m. As indicated by Cornish-Bowden et al. [2,10], the unitary values of V_max and K_m involved no loss of generality because they finally depend on the units of measurement. The values of substrate and product concentrations are listed in Table 1, corresponding to n = 7 and m = 5, according to the nomenclature in the scheme of Figure 1.

The chosen values of substrate concentrations were based on their distribution around the K_m value from 0.1 K_m to 10 K_m, with three values below K_m and three values above K_m, as recommended by Cornish-Bowden [11]. In the case of product concentrations, the choice was based on a K_p value-centered distribution. The experimental design consisted of 35 reaction rates (v_ij), which were calculated using the product-competitive inhibition equation (Equation (1)) assigning relative errors from a normal population of error ε_i with variance σ² (Equation (7)) to simulate the experimental error.

$$v_{ij}=\frac{V_{max}{S}_{ij}}{K_m+S_{ij}+\frac{K_m}{K_p}{P}_j}\left(1+{\epsilon }_i\right)$$

(7)

The calculated reaction rates (v_ij) were used as experimental values to estimate the kinetic constants V_max, K_m, and K_p. The estimations were carried out by DLP, using Equation (4), and by the LS method. The number of possible combinations of three initial rate values (v_ij) to calculate the kinetic constants V_max, K_m, and K_p was 6370, according to Equations (4) and (5). The median for each kinetic constant was obtained from this list. This procedure corresponded to one experiment to calculate the estimators of the kinetic constants, which is equivalent to an empirical procedure based on the initial rates method. A total of 1000 experiments were run to compare the accuracy of both methods and the quality of parameter estimations. An algorithm was written in Python software to perform all the calculations presented in this article. The algorithm can be downloaded from the repository indicated in the Supplementary Material. Estimation of K_p was carried out by two optional procedures: (i) calculating K_m/K_p for each of the 1000 experiments, calculating the median for K_m/K_p, and finally obtaining the estimated K_p using the corresponding K_m value, and (ii) calculating the K_p for each of the 1000 experiments and calculating the median of K_p (see Equation (5)). In the case of the LS method, a non-linear regression was applied to Equation (8), where the apparent K_m ($K_m^{app}$) was estimated. According to the experimental design, five values of V_max and $K_m^{app}$ were obtained, one for each product concentration. As V_max is not affected by competitive inhibition, a higher value was chosen as the estimated V_max through the LS method. The $K_m^{app}$ values were plotted against the product concentrations in a secondary plot, and the values of K_m and K_p were obtained by linear regression of Equation (9).

$$v=\frac{V_{max}S}{K_m^{app}+S}$$

(8)

$$K_m^{app}=K_m+\frac{K_m}{K_p}P$$

(9)

The effect of the K_p/K_m ratio was also evaluated. The values of K_p considered were 10, 20, 50, 100, and 200. The K_p/K_m ratios corresponded to the same values, considering that K_m was 1. As the values of K_p were modified, the experimental values of product concentration (P) were changed to maintain the same values of apparent K_m, according to Equation (9), among the different datasets to avoid negative effects in the experimental design.

3.2. Accuracy Test

The sum of squared residuals (SSR) was calculated for each of the 1000 experiments for both methods, DLP and LS, to evaluate their accuracies, according to Equation (10).

$$SSR={\displaystyle \sum }_{i=1}^n\left(v_i-{\widehat{v}}_i\right)$$

(10)

where $v_i$ is the i^th value of the experimental rate (Equation (7)), and ${\widehat{v}}_i$ is the i^th value of the predicted rate calculated according to Equation (1). The relative error (e_i) from the difference between the real ($\theta$) and the estimated value ($\widehat{\theta }$) was calculated for all kinetic constants according to Equation (11).

$$e_i=\left|\frac{\widehat{\theta }-\theta }{\theta }\right|$$

(11)

The number of experiments (out of 1000) in which the LS resulted in a lower SSR and e_i was calculated and compared with DLP for different values of the variance σ² for error ε_i.

3.3. Effect of Outliers

The sensitivity of both methods to outliers was tested by changing the initial rate value v₃₄ from Table 1. This value corresponds to the substrate concentration equal to K_m and the product concentration equal to K_p. The initial rate v₃₄ was changed by varying fixed values of ε_i from −0.1 to +0.1. The rest of the experimental initial rates were calculated as mentioned above using Equation (6) with random ε_i with σ² = 0.01. The perturbation generated on the estimated constant was calculated according to Equation (12).

$$\%Perturbation=\frac{{\widehat{\theta }}_u-{\widehat{\theta }}_l}{\theta }·100$$

(12)

where ${\widehat{\theta }}_u$ and ${\widehat{\theta }}_l$ are the upper and lower estimated values of the real constant $\theta$ in the range of the fixed error.