Modified Catalysts and Their Fractal Properties
Abstract
:1. Introduction
2. Results
2.1. Influences of Synthesis Parameters on the Fractal Dimension
2.1.1. Precursor Type Influences the Fractal Dimension of Perovskite
2.1.2. The Dopant (Sr) Influences the Fractal Dimension. The Limits of Self-Similarity
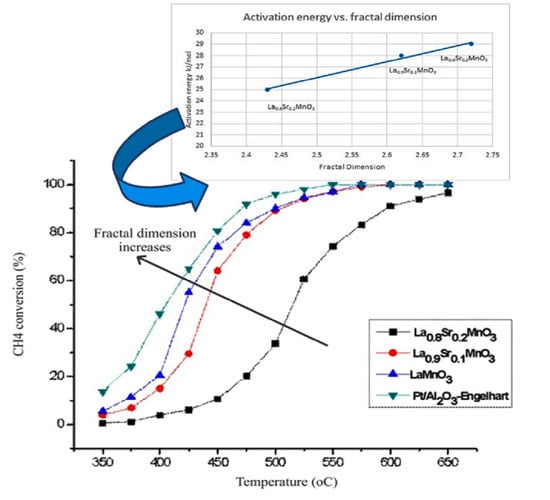
2.2. The Dependence of the Fractal Dimension on Catalytic Activity
2.3. The Fractal Structure of Mono- and Bi-Metallic Nanoparticles
2.4. The Influence of the Fractal Dimension of Supported Nanoparticles on Surface Basicity
3. Discussion Regarding the Fractal Properties of Catalysts
4. Materials and Methods
4.1. Synthesis of Materials
4.2. Methods
4.2.1. Fractal Dimension Determination Using Image Analysis
4.2.2. Fractal Dimension Determination Using Adsorption Isotherms
- -
- the BET fractal isotherm obtained by Fripiat [57]:
- -
- the Frenkel-Halsey-Hill [58] isotherm:
4.2.3. Avnir–Jaroniec Method
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mandelbrot, B.B. Fractals: Form, Chance and Dimension; Freeman, W.H., Ed.; MANDELBROT. WH Freeman and Co.: San Francisco, CA, USA, 1977. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman, W.H., Ed.; MANDELBROT. WH Freeman and Co.: San Francisco, CA, USA, 1982. [Google Scholar]
- Sorensen, C.M. Light scattering by fractal aggregates: A review. Aerosol Sci. Technol. 2001, 35, 648–687. [Google Scholar] [CrossRef]
- Abed, A.T.; Abu-AlShaer, M.J.; Jawad, A.M. Fractal antennas for wireless communications. In Modern Printed-Circuit Antennas; Al-Rizzo, H., Ed.; IntechOpen: London, UK, 2020. [Google Scholar]
- Witten, T.A.; Sander, L.M. Diffusion-limited aggregation. Phys. Rev. B 1983, 27, 5686–5697. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.W.; Xie, H. Direct estimation of the fractal dimensions of a fracture surface of rock. Surf. Rev. Lett. 2003, 10, 751–762. [Google Scholar] [CrossRef]
- Kopelman, R. Fractal Reaction Kinetics. Science 1988, 241, 1620–1626. [Google Scholar] [CrossRef] [PubMed]
- Mattfeldt, H.W.; Gottfried, H.W.; Schmidt, V.; Kestler, H.A. Classification of spatial textures in benign and cancerous glandular tissues by stereology and stochastic geometry using artificial neural networks. J. Microsc. 1999, 198, 143–158. [Google Scholar]
- Socoteanu, R.; Anastasescu, M.; Dobrescu, G.; Boscencu, R.; Vasiliu, G.; Constantin, C. AFM imaging, fractal analysis and in vitro cytotoxicity evaluation of Zn (II) vs. Cu (II) porphyrins. Chaos Solit. Fractals 2015, 77, 304–309. [Google Scholar] [CrossRef]
- Hang, J.T.; Kang, Y.; Xu, G.-K.; Gao, H. A hierarchical cellular structural model to unravel the universal power-law rheological behavior of living cells. Nat. Commun. 2021, 12, 6067. [Google Scholar] [CrossRef] [PubMed]
- Avnir, D.; Farin, D.; Pfeifer, P. Surface geometric irregularity of particulate materials: The fractal approach. J. Colloid Interface Sci. 1985, 103, 112–123. [Google Scholar] [CrossRef]
- Rothschild, W.G. Fractals in heterogeneous catalysis. Catal. Rev. Sci. Eng. 1991, 33, 71–107. [Google Scholar] [CrossRef]
- Pfeifer, P.; Obert, M.; Cole, M.W. Fractal BET and FHH theories of adsorption: A comparative study. Proc. R. Soc. Lond. A 1989, 423, 169–188. [Google Scholar]
- Pfeifer, P.; Avnir, D.; Farin, D. Complex Surface Geometry in Nano-Structure Solids: Fractal Versus Bernal-Type Models. Large Scale Molecular Systems—Quantum and Stochastic Aspects; NATO ASI, Series B; Gans, W., Blumen, A., Amann, A., Eds.; Plenum: New York, NY, USA, 1991; pp. 215–229. [Google Scholar]
- Meakin, P. Fractals and Reactions on Fractals. In Reactions in Compartmentalized Liquids; Knoche, W., Schomäcker, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 173–198. [Google Scholar]
- Avnir, D.; Jaroniec, M. An isotherm equation for adsorption on fractal surfaces of heterogeneous porous materials. Langmuir 1989, 5, 1431–1433. [Google Scholar] [CrossRef]
- Pfeifer, P.; Kenntner, J.; Cole, M.W. Detecting capillary condensation in the absence of adsorption/desorption hysteresis. In Fundamentals of Adsorption; American Institute of Chemical Engineers: New York, NY, USA, 1991; pp. 689–700. [Google Scholar]
- Ludlow, D.K.; Moberg, T.P. Technique for determination of surface fractal dimension using a dynamic flow adsorption instrument. Instrum. Sci. Technol. 1990, 19, 113–123. [Google Scholar] [CrossRef]
- Farin, D.; Avnir, D.; Pfeifer, P. Fractal dimensions of surfaces. The use of adsorption data for the quantitative evaluation of geometric irregularity. Particul. Sci. Technol. 1984, 2, 27–35. [Google Scholar] [CrossRef]
- Pfeifer, P.; Stella, A.L.; Toigo, F.; Cole, M.W. Scaling of the dynamic structure factor of an adsorbate on a fractal surface. Europhys. Lett. 1987, 3, 717–722. [Google Scholar] [CrossRef]
- Cheng, E.; Cole, M.W.; Pfeifer, P. Defractalization of films adsorbed on fractal surfaces. Phys. Rev. B 1989, 39, 12962–12965. [Google Scholar] [CrossRef]
- Avnir, D.; Farin, D. Fractal scaling laws in heterogeneous chemistry: Part I: Adsorptions, chemisorptions and interactions between adsorbates. N. J. Chem. 1990, 14, 197–206. [Google Scholar]
- Pfeifer, P.; Johnston, G.P.; Deshpande, R.; Smith, D.M.; Hurd, A.J. Structure analysis of porous solids from preadsorbed films. Langmuir 1991, 7, 2833–2843. [Google Scholar] [CrossRef]
- Kaneko, K.; Sato, M.; Suzuki, T.; Fujiwara, Y.; Nishikawa, K.; Jaroniec, M. Surface fractal dimension of microporous carbon fibres by nitrogen adsorption. J. Chem. Soc. Faraday Trans. 1991, 87, 179–184. [Google Scholar] [CrossRef]
- Gutfraind, R.; Sheintuch, M.; Avnir, D. Fractal and multifractal analysis of the sensitivity of catalytic reactions to catalyst structure. J. Chem. Phys. 1991, 95, 6100–6111. [Google Scholar] [CrossRef]
- Sanders, L.M.; Ghaisas, S.V. Fractals and patterns in catalysis. Phys. A 1996, 233, 629–639. [Google Scholar] [CrossRef]
- Che, M.; Bennett, C.O. The influence of particle size on the catalytic properties of supported metals. Adv. Catal. 1989, 36, 55–172. [Google Scholar]
- Matsubu, J.; Zhang, S.; DeRita, L.; Marinkovic, N.S.; Chen, J.G.; Graham, G.W.; Pan, X.; Christopher, P. Adsorbate-mediated strong metal–support interactions in oxide-supported Rh catalysts. Nat. Chem. 2017, 9, 120–127. [Google Scholar]
- Huang, R.; Wu, J.; Zhang, M.; Liu, B.; Zheng, Z.; Luo, D. Strategies to enhance photocatalytic activity of graphite carbon nitride-based photocatalysts. Mater. Des. 2021, 210, 110040. [Google Scholar]
- Dobrescu, G.; Berger, D.; Papa, F.; Fangli, I.; Rusu, M. Fractal dimensions of lanthanum cobaltites samples by adsorption isotherm method. In Interdisciplinary Applications of Fractal and Chaos Theory; Dobrescu, R., Vasilescu, C., Eds.; Editura Academiei Romane: Bucuresti, Romania, 2004; pp. 295–302. [Google Scholar]
- Dobrescu, G.; Berger, D.; Papa, F.; Ionescu, N.I. Fractal dimension of lanthanum ferrite samples by adsorption isotherm method. Appl. Surf. Sci. 2003, 220, 154–158. [Google Scholar] [CrossRef]
- Dobrescu, G.; Berger, D.; Papa, F.; Ionescu, N.I.; Rusu, M. Fractal analysis of micrographs and adsorption isotherms of La1−xSrxCoO3 samples. J. Optoelectron. Adv. 2003, 5, 1433–1437. [Google Scholar]
- Wojsk, R.; Terzyk, A.P. The structural parameters of microporous solid, including fractal dimension, on the basis of the potential theory of adsorption-the general solution. Comput. Chem. 1997, 21, 83–87. [Google Scholar]
- Papa, F.; Berger, D.; Dobrescu, G.; State, R.; Ionescu, N.I. Correlation of the Sr-dopant content in La1−xSrxCoO3 with catalytic activity for hydrogen peroxide decomposition. Rev. Roum. Chim. 2018, 63, 447–453. [Google Scholar]
- Aoa, M.; Pharma, G.H.; Sage, V.; Pareeka, V. Structure and activity of strontium substituted LaCoO3 perovskite catalysts forsyngas conversion. J. Mol. Catal. A Chem. 2016, 416, 96–104. [Google Scholar] [CrossRef]
- Prasad, D.H.; Park, S.Y.; Oh, E.O.; Ji, H.; Kim, H.R.; Yoon, K.J.; Yoon, J.; Son, J.W.; Lee, J.H. Synthesis of nano-crystalline La1−xSrxCoO3-δ perovskite oxides by EDTA-citrate complexing process and its catalytic activity for soot oxidation. Appl. Catal. A Gen. 2012, 447, 100–106. [Google Scholar] [CrossRef]
- Trypolskyi, A.I.; Gurnyk, T.M.; Strizhak, P.E. Fractal dimension of zirconia nanopowders and their activity in the CO oxidation. Catal. Commun. 2011, 12, 766–771. [Google Scholar] [CrossRef]
- Dobrescu, G.; Papa, F.; State, R.; Balint, I. Characterization of bimetallic nanoparticles by fractal analysis. Powder Technol. 2018, 338, 905–914. [Google Scholar] [CrossRef]
- Miyazaki, A.; Matsuda, K.; Papa, F.; Scurtu, M.; Negrila, C.; Dobrescu, G.; Balint, I. Impact of particle size and metal-support interaction on denitration behavior of wee-defined Pt-Cu nanoparticles. Catal. Sci. Technol. 2015, 5, 492–503. [Google Scholar] [CrossRef]
- Lanza, R.; Canu, P.; Jaras, S.G. Partial oxidation of methane over Pt-Ru bimetallic catalyst for syngas production. Appl. Catal. A Gen. 2008, 348, 221–228. [Google Scholar] [CrossRef]
- Liao, P.C.; Carberry, J.J.; Fleisch, T.H.; Wolf, E.E. CO oxidation activity and XPS studies of PtCuγ-Al2O3 bimetallic catalysts. J. Catal. 1982, 74, 307–316. [Google Scholar] [CrossRef]
- Soares, O.S.G.P.; Órfão, J.J.M.; Pereira, M.F.R. Bimetallic catalysts supported on activated carbon for the nitrate reduction in water: Optimization of catalysts composition. Appl. Catal. B Environ. 2009, 91, 441–448. [Google Scholar] [CrossRef]
- Baglio, V.; Stassi, A.; Di Blasi, A.; D’Urso, C.; Antonucci, V.; Arico, A.S. Investigation of bimetallic Pt-M/C as DMFC cathode catalysts. Electrochim. Acta 2007, 53, 1360. [Google Scholar] [CrossRef]
- Papa, F.; Negrila, C.; Dobrescu, G.; Miyazaki, A.; Balint, I. Preparation, characterization and catalytic behavior of Pt-Cu nanoparticles in methane combustion. J. Nat. Gas Chem. 2011, 20, 537–542. [Google Scholar] [CrossRef]
- Dobrescu, G.; Papa, F.; Atkinson, I.; Culita, D.; Balint, I. Correlation between the basicity and the fractal dimension of Rh-nanoparticles supported on Al2O3, TiO2 and WO3. IOSR-JAC 2021, 14, 11–25. [Google Scholar]
- Jang, W.; Shim, J.; Kim, H.; Yoo, S.; Roh, H. A review on dry reforming of methane in aspect of catalytic properties. Catal. Today 2019, 324, 15–26. [Google Scholar] [CrossRef]
- Wang, H.Y.; Ruckenstein, E. Carbon dioxide reforming of methane to synthesis gas over supported rhodium catalysts: The effect of support. Appl. Catal. A Gen. 2000, 204, 143–152. [Google Scholar] [CrossRef]
- Curtis Conner, W.; Bennett, C.O. Are the pore and surface morphologies of real fractal catalysts? J. Chem. Soc. Faraday Trans. 1993, 89, 4109–4114. [Google Scholar] [CrossRef]
- Rudzinski, W.; Lee, S.L.; Sanders yan, C.C.; Panczyk, T. A fractal approach to adsorption on heterogeneous solid surfaces. 1. The relationship between geometric and energetic surface heterogeneities. J. Phys. Chem. B 2001, 105, 10847–10856. [Google Scholar] [CrossRef]
- Berger, D.; Matei, C.; Papa, F.; Voicu, G.; Fruth, V. Pure and doped LaCoO3 obtained by combustion method. Prog. Solid State Chem. 2007, 35, 183–191. [Google Scholar] [CrossRef]
- Dobrescu, G.; Berger, D.; Papa, F.; Fangli, I.; Sitaru, I. Fractal analysis of micrographs and adsorption isotherms of LaCoO3 and LaFeO3 samples. Ann. West Univ. Timis. Ser. Chem. 2003, 12, 1505–1512. [Google Scholar]
- Papa, F.; Negrila, C.; Miyazaki, A.; Balint, I. Morphology and chemical state of PVP-protected Pt, Pt-Cu and Pt-Ag nanoparticles prepared by alkaline polyol method. J. Nanopart. Res. 2011, 13, 5057–5064. [Google Scholar] [CrossRef]
- Schepers, H.E.; van Beek, J.H.G.M.; Bassingthwaighte, J.B. Four methods to estimate the fractal dimension from self-affine signals (medical application). IEEE Eng. Med. Biol. 1992, 11, 57–64. [Google Scholar] [CrossRef] [Green Version]
- Botet, R.; Jullien, R. A theory of aggregating systems of particles: The clustering of clusters process. Ann. Phys. Fr. 1988, 13, 153–221. [Google Scholar] [CrossRef]
- Family, F.; Vicsek, T. Scaling of the active zone in the Eden process on percolation networks and the ballistic deposition model. J. Phys. A Math. Gen. 1985, 18, L75–L81. [Google Scholar] [CrossRef]
- Chauvy, P.F.; Madore, C.; Landolt, D. Variable length scale analysis of surface topography: Characterization of titanium surfaces for biomedical applications. Surf. Coat. Technol. 1998, 110, 48–56. [Google Scholar] [CrossRef]
- Fripiat, I.J.; Gatineau, L.; van Damme, H. Multilayer physical adsorption on fractal surfaces. Langmuir 1986, 2, 562–567. [Google Scholar] [CrossRef]
- Pfeifer, P.; Wu, Y.J.; Cole, M.W.; Krim, J. Multilayer adsorption on a fractally rough surface. Phys. Rev. Lett. 1989, 62, 1997–2000. [Google Scholar] [CrossRef] [PubMed]










| Precursor | Fractal Dimension DR Isotherm | Fractal Dimension AJ Method | BET Surface (m2/g) |
|---|---|---|---|
| Maleic acid | 2.3±0.06 | 2.34 ± 0.06 Fractional filling 0.40–0.80 | 20.42 |
| Alpha-alanine | 2.62±0.06 | 2.62 ± 0.06 Fractional filling 0.68–0.88 | 32.50 |
| Urea | 2.43±0.03 | 2.43 ± 0.03 Fractional filling 0.45–0.82 | 22.62 |
| Precursor | Fractal Dimension DR Isotherm Fitting | Fractal Dimension Avnir–Jaroniec Method |
|---|---|---|
| Maleic acid | 2.11 ± 0.04 | 2.07 ± 0.01 0.4–0.6 (fractional filling range) |
| Alpha-alanine | 2.42 ± 0.02 | 2.44 ± 0.05 0.46–0.93 (fractional filling range) |
| Urea | 2.40 ± 0.02 | 2.49 ± 0.01 0.77–0.86 (fractional filling range) |
| x | SEM Analysis | Self-Similarity Limits (nm) (SEM Analysis) | Fractal Dimension (DR Adsorption Isotherm) |
|---|---|---|---|
| 0 | 2.32 ± 0.01 | 250–1110 | 2.34 ± 0.06 |
| 0.1 | 2.51 ± 0.02 | 100–440 | 2.58 ± 0.02 |
| 0.2 | 2.43 ± 0.01 | 30–330 | 2.48 ± 0.01 |
| Sample | Fractal Dimension | Determination Coefficient |
|---|---|---|
| LaCoO3 | 2.39 ± 0.03 | 0.987 |
| La0.9Sr0.1CoO3 | 2.45 ± 0.01 | 0.989 |
| La0.8Sr0.2CoO3 | 2.48 ± 0.01 | 0.999 |
| La0.7Sr0.3CoO3 | 2.62 ± 0.03 | 0.970 |
| Samples | Method | Fractal Dimension | Determination Coefficient | Self-Similarity Limit (nm) |
|---|---|---|---|---|
| LaMnO3-alanine | SEM—correlation function method | 2.49 ± 0.01 | 0.999 | 100–282 |
| 2.70 ± 0.01 | 0.983 | 282–2326 | ||
| SEM—variable scale method | 2.53 ± 0.02 | 0.998 | 1000–4000 | |
| 2.74 ± 0.01 | 0.992 | 4000–12,000 | ||
| DR fractal isotherm | 2.54 ± 0.04 | 0.972 | - | |
| La0.9Sr0.1MnO3 | SEM—correlation function method | 2.20 ± 0.01 | 0.994 | 20–116 |
| 2.62 ± 0.01 | 0.984 | 116–820 | ||
| DR fractal isotherm | 2.19 ± 0.02 | 0.975 | - | |
| La0.8Sr0.2MnO3 | SEM—correlation function method | 2.18 ± 0.01 | 0.996 | 20–136 |
| 2.43 ± 0.01 | 0.988 | 136–700 | ||
| SEM—variable scale method | - | - | - | |
| DR fractal isotherm | 2.20 ± 0.02 | 0.989 | - |
| Sample | Fractal Dimension D0 | Lacunarity A0 |
|---|---|---|
| Pd | 1.427 ± 0.457 | 8.39 × 104 |
| Pd-Cu 4:1 Alloy | 1.912 ± 0.014 | 8.24 × 105 |
| Pd-Cu 1:1 Alloy | 1.681 ± 0.015 | 2.57 × 105 |
| Pd-Cu 1:4 Alloy | 1.799 ± 0.035 | 2.36 × 105 |
| Sample | D0 | λm | D (λm) | λ1 | D (λ1) | λ2 | D (λ2) |
|---|---|---|---|---|---|---|---|
| Pd-Cu Core-shell | 1.841 ± 0.009 | 140 | 1.773 ± 0.048 | 170 | 1.632 ± 0.074 | 130 | 1.826 ± 0.037 |
| Cu-Pd Inverse core-shell | 1.855 ± 0.010 | 110 | 1.796 ± 0.026 | 130 | 1.827 ± 0.029 | 100 | 1.813 ± 0.010 |
| Pd-Ag Core-shell | 1.854 ± 0.018 | 130 | 1.819 ± 0.107 | 160 | 1.669 ± 0.061 | 120 | 1.863 ± 0.079 |
| Ag-Pd Inverse Core-shell | 1.875 ± 0.032 | 100 | 1.836 ± 0.023 | 110 | 1.776 ± 0.018 | 90 | 1.884 ± 0.021 |
| Sample | Calculation Method | Fractal Dimension | Correlation Coefficient | Self-Similarity Domain/nm |
|---|---|---|---|---|
| (Pt-Cu)L | Correlation function | 2.50 ± 0.01 | 0.991 | 1.4–2.5 |
| 2.70 ± 0.01 | 0.981 | 2.5–5.0 | ||
| Variable length scale | 2.68 ± 0.01 | 0.984 | 5.0–27.5 | |
| (Pt-Cu)S | Correlation function | 2.40 ± 0.01 | 0.998 | 1.4–2.2 |
| 2.73 ± 0.01 | 0.996 | 7.5–12.5 | ||
| Variable length scale | 2.88 ± 0.01 | 0.992 | 12.5–22.5 |
| Fractal Dimension | Linear Correlation Coefficient | Self-Similarity Domain |
|---|---|---|
| 2.39 ± 0.01 | 0.996 | 0.18–1.24 |
| 2.81 ± 0.01 | 0.975 | 1.24–4.50 |
| Sample | Fractal Dimension | Correlation Coefficient | Self-Similarity Domain (nm) |
|---|---|---|---|
| Rh/Al2O3 | 2.872 ± 0.001 (C) | 0.9910 | 4.4–14.4 |
| 2.784 ± 0.051 (S) | 0.8186 | 7.2–11.8 | |
| Al2O3 | 2.952 ± 0.001 (C) | 0.9375 | 0.7–8.1 |
| 2.962 ± 0.004 (S) | 0.9549 | 1.4–2.8 | |
| Rh/TiO2 | 2.733 ± 0.001 (C) | 0.9884 | 4.9–14.4 |
| 2.832 ± 0.009 (S) | 0.9649 | 5.4–17.3 | |
| TiO2 | 2.831 ± 0.001 (C) | 0.857 | 6.5–11 |
| 2.911 ± 0.017 (S) | 0.925 | 2.4–3.00 | |
| Rh/WO3 | 2.490 ± 0.001 (C) | 0.9975 | 0.2–2.7 |
| 2.330 ± 0.001 (C) | 0.9991 | 2.7–13.8 | |
| 2.469 ± 0.035 (S) | 0.9747 | 4.5–11 | |
| 2.226 ± 0.047 (S) | 0.9334 | 11–29.3 | |
| WO3 | 2.660 ± 0.004 (C) | 0.990 | 0.2–1.2 |
| 2.293 ± 0.002 (C) | 0.986 | 1.8–5.0 | |
| 2.652 ± 0.042 (S) | 0.949 | 4.1–5.9 |
| Sample | Fractal Dimension | Correlation Coefficient | Self-Similarity Domain (p/p0) | CO2-TPD |
|---|---|---|---|---|
| Rh/Al2O3 | 2.607 ± 0.004 | 0.9986 | 0.033–0.850 | Before |
| 2.534 ± 0.009 | 0.9973 | 0.011–0.350 | After | |
| 2.623 ± 0.002 | 0.9998 | 0.350–0.800 | After | |
| Rh/TiO2 | 2.604 ± 0.003 | 0.9989 | 0.011–0.750 | Before |
| 2.292 ± 0.011 | 0.9980 | 0.005–0.350 | After | |
| 2.548 ± 0.005 | 0.9987 | 0.350–0.850 | After | |
| Rh/WO3 | 2.448 ± 0.012 | 0.9977 | 0.005–0.200 | Before |
| 2.589 ± 0.014 | 0.9889 | 0.200–0.750 | Before | |
| 2.595 ± 0.008 | 0.9970 | 0.005–0.350 | After | |
| 2.003 ± 0.003 | 0.9993 | 0.350–0.875 | After |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dobrescu, G.; Papa, F.; State, R.; Raciulete, M.; Berger, D.; Balint, I.; Ionescu, N.I. Modified Catalysts and Their Fractal Properties. Catalysts 2021, 11, 1518. https://doi.org/10.3390/catal11121518
Dobrescu G, Papa F, State R, Raciulete M, Berger D, Balint I, Ionescu NI. Modified Catalysts and Their Fractal Properties. Catalysts. 2021; 11(12):1518. https://doi.org/10.3390/catal11121518
Chicago/Turabian StyleDobrescu, Gianina, Florica Papa, Razvan State, Monica Raciulete, Daniela Berger, Ioan Balint, and Niculae I. Ionescu. 2021. "Modified Catalysts and Their Fractal Properties" Catalysts 11, no. 12: 1518. https://doi.org/10.3390/catal11121518
APA StyleDobrescu, G., Papa, F., State, R., Raciulete, M., Berger, D., Balint, I., & Ionescu, N. I. (2021). Modified Catalysts and Their Fractal Properties. Catalysts, 11(12), 1518. https://doi.org/10.3390/catal11121518