Effect of Temperature on Luminescence of LiNbO3 Crystals Single-Doped with Sm3+, Tb3+, or Dy3+ Ions
Abstract
:1. Introduction
2. Materials and Methods
3. Results
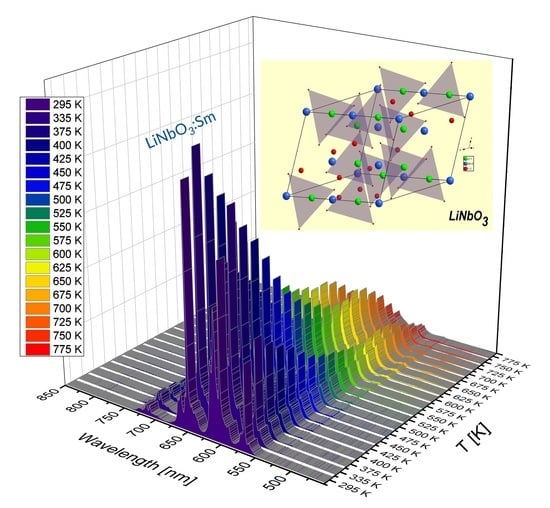
3.1. Effect of Temperature on Luminescence of Sm3+ and Dy3+ in LiNbO3
3.2. Effect of Temperature on Luminescence of Tb3+ in LiNbO3 and LiTaO3
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Boyd, G.D.; Miller, R.C.; Nassau, K.; Bond, W.L.; Savage, A. LiNbO3: An efficient phase matchable nonlinear optical material. Appl. Phys. Lett. 1964, 5, 234. [Google Scholar] [CrossRef]
- Lee, M.; Takedawa, S.; Furukawa, Y.; Kitamura, K.; Hatano, H.; Tanaka, S. Nonvolatile two-color holographic recoding in Tb-doped LiNbO3. Appl. Phys. Lett. 2000, 76, 1653–1655. [Google Scholar] [CrossRef]
- Adibi, A.; Buse, K.; Psaltis, D. Two-center holographic recording. J. Opt. Soc. Am. B 2001, 18, 584–601. [Google Scholar] [CrossRef]
- Myers, L.E.; Eckhardt, R.C.; Fejer, M.M.; Byer, R.L.; Bosenberg, W.R.; Pierce, J.W. Quasi-phase-matched optical parametric oscillations in bulk periodically poled LiNbO3. J. Opt. Soc. Am. 1995, B12, 21022116. [Google Scholar] [CrossRef]
- Ross, G.W.; Pollnau, M.; Smith, P.G.R.; Clarkson, W.A.; Britton, P.E.; Hanna, D.C. Generation of high-power blue light in periodically poled LiNbO3. Opt. Lett. 1998, 23, 171–173. [Google Scholar] [CrossRef]
- Lallier, E.; Pachole, J.P.; Papuchon, M.; Micheli, M.; Li, M.J.; He, Q.; Ostrovsky, D.B.; Grezes-Besset, C.; Pelletier, E. Nd:Mgo:LiNbO3 waveguide laser and amplifier. Opt. Lett. 1990, 15, 682–684. [Google Scholar] [CrossRef]
- Amin, J.; Aust, J.A.; Veasey, D.L.; Sanfard, N.A. Dual wavelength 980 nm pumped Er/Yb-codoped waveguide laser in Ti:LiNbO3. Electron. Lett. 1998, 34, 456–458. [Google Scholar] [CrossRef]
- Li, R.; Wang, C.J.; Liang, X.; Peng, K.; Xu, G. CW Nd:Mg:LiNbO3 self-frequency-doubling laser at room temperature. IEEE J. Quantum Electron. 1993, 29, 2419–2420. [Google Scholar] [CrossRef]
- Jiangou, Z.; Shipin, Z.; Dingquan, X.; Xiu, W.; Guanfeng, X. Optical absorption properties of doped lithium niobate crystals. J. Phys. Condens. Matter. 1992, 4, 2977. [Google Scholar] [CrossRef]
- Kase, S.; Ohi, K. Optical absorption and interband Faraday rotation in LiTaO3 and LiNbO3. Ferroelectrics 1974, 8, 419. [Google Scholar] [CrossRef]
- Schmidt, W.G.; Albrecht, M.; Wippermann, S.; Blankenburg, S.; Rauls, E.; Fuchs, F.; Rodl, C.; Furthmuller, J.; Hermann, A. LiNbO3 ground- and excited-state properties from first-principles calculations. Phys. Rev. B 2006, 77, 035106. [Google Scholar] [CrossRef]
- Thierfelder, C.; Sanna, S.; Schindlmayr, A.; Schmidt, W.G. Do we know the band gap of lithium niobate? Phys. Stat. Solidi C 2010, 7, 362–365. [Google Scholar] [CrossRef]
- Mamoun, S.; Merad, A.E.; Guilbert, L. Energy band gap and optical properties of lithium niobate from ab initio calculations. Comp. Mater. Sci. 2013, 79, 125–131. [Google Scholar] [CrossRef]
- Abrahams, S.C.; Marsh, P. Defect structure dependence on composition in lithium niobate. Acta Cryst. B 1986, 42, 61. [Google Scholar] [CrossRef]
- Iyi, N.; Kitamura, K.; Izumi, F.; Yamamoto, J.K.; Hayashi, K.; Asano, H.; Kimura, J. Comparative study of defect structures in lithium niobate with different compositions. J. Solid State Chem. 1992, 101, 340. [Google Scholar] [CrossRef]
- Zotov, N.; Boysen, H.; Frey, F.; Metzger, T.; Born, E. Cation substitution models of congruent LiNbO3 investigated by X-ray and neutron powder diffraction. J. Phys. Chem. Solids 1994, 55, 145–152. [Google Scholar] [CrossRef]
- Lorenzo, A.; Jaffrezic, H.; Roux, B.; Boulon, G.; Garcia-Sole, J. Lattice location of rare earth ions in LiNbO3. Appl. Phys. Lett. 1995, 67, 3735. [Google Scholar] [CrossRef]
- Gasparotto, G.; Cebim, M.A.; Goes, M.S.; Lima, S.A.M.; Davolos, M.R.; Varela, J.A.; Paiva-Santos, C.O.; Zaghete, M.A. Correlation between the spectroscopic and structural properties with the occupation of the Eu3+ sites in powdered Eu3+-doped LiTaO3 prepared by the Pechini method. J. Appl. Phys. 2009, 106, 063509. [Google Scholar] [CrossRef] [Green Version]
- Shu, S.; Wang, Y.; Ke, Y.; Deng, B.; Liu, R.; Song, Q.; Wang, J.; Yu, R. NaCaTiTaO6:Sm3+: A novel orange-red-emitting tantalate phosphor with excellent thermal stability and high color purity for white LEDs. J. Alloy. Compd. 2020, 848, 156359. [Google Scholar] [CrossRef]
- Su, K.; Zhang, Q.; Yang, X.; Ma, B. Crystal structure and luminescence properties of thermally stable Sm3+-doped Sr9In(PO4)7 orange-red phosphor. J. Phys. D Appl. Phys. 2020, 53, 385101. [Google Scholar] [CrossRef]
- Zhang, L.; Che, J.; Ma, Y.; Wang, J.; Kang, R.; Deng, B.; Yu, R.; Geng, H. Luminescent and thermal properties of novel orange-red emitting Ca2MgTeO6:Sm3+ phosphors for white LED’s. J. Lumin. 2020, 225, 117374. [Google Scholar] [CrossRef]
- Kovács, L.; Kocsor, L.; Tichy-Rács, É.; Lengyel, K.; Bencs, L.; Corradi, G. Hydroxyl ion probing transition metal dopants occupying Nb sites in stoichiometric LiNbO3. Opt. Mater. Express 2019, 9, 4506–4516. [Google Scholar] [CrossRef]
- Mandula, G.; Kis, Z.; Kovacs, L.; Szaller, Z.; Krampf, A. Site-selective measurement of relaxation properties at 980 nmin Er3+-doped congruent and stoichiometric lithium niobite crystals. Appl. Phys. B 2016, 122, 72. [Google Scholar] [CrossRef]
- Kis, Z.; Mandula, G.; Lengyel, K.; Hajdara, I.; Kovacs, L.; Imlau, M. Homogeneous linewidth measurements of Yb3+ ions in congruent and stoichiometric lithium niobate crystals. Opt. Mater. 2014, 37, 845–853. [Google Scholar] [CrossRef]
- Robbins, D.J.; Cockayne, B.; Lent, B.; Glasper, J.L. The mechanism of 5D3–5D4 cross-relaxation in Y3Al5O12:Tb3+. Solid State Commun. 1976, 20, 673–676. [Google Scholar] [CrossRef]
- Park, J.Y.; Jung, H.C.; Raju, S.R.; Moon, B.K.; Jeong, J.H.; Kim, J.H. Solvothermal synthesis and luminescence properties of Tb3+-doped gadolinium aluminum garnet. J. Lumin. 2010, 130, 478–482. [Google Scholar] [CrossRef]
- Praveena, R.; Shim, J.J.; Cai, P.; Seo, H.J.; Chung, W.; Kwon, T.H.; Jayasankar, C.K.; Haritha, P.; Venkatramu, V. Luminescence properties of Lu3Al5O12:Tb3+ nano-garnet. J. Korean Phys. Soc. 2014, 64, 1859–1865. [Google Scholar] [CrossRef]
- Teng, X.; Wang, W.; Cao, Z.; Li, J.; Duan, G.; Liu, Z. The development of new phosphors 3f Tb3+/Eu3+ co-doped Gd3Al5O12 with tunable emission. Opt. Mater. (Amst.) 2017, 69, 175–180. [Google Scholar] [CrossRef]
- Solarz, P.; Głowacki, M.; Lisiecki, R.; Sobczyk, M.; Komar, J.; Macalik, B.; Ryba-Romanowski, W. Impact of temperature on excitation, emission and cross-relaxation processes of terbium ions in GGAG single crystal. J. Alloy. Compd. 2019, 789, 409–415. [Google Scholar] [CrossRef]
- Hakeem, D.A.; Pi, J.W.; Kim, S.W.; Park, K. New Y2LuCaAl2SiO12:Ln (Ln = Ce3+, Eu3+, and Tb3+) phosphors for white LED applications. Inorg. Chem. Front. 2018, 5, 1336–1345. [Google Scholar] [CrossRef]
- Deopa, N.; Rao, A.S. Spectroscopic studies of single near ultraviolet pumped Tb3+ doped Lithium Lead Alumino Borate glasses for green lasers and tricolour w-LEDs. J. Lumin. 2018, 194, 56–63. [Google Scholar] [CrossRef]
- Loiko, P.; Volokitina, A.; Mateos, X.; Dunina, E.; Kornienko, A.; Vilejshikova, E.; Aguiló, M.; Díaz, F. Spectroscopy of Tb3+ ions in monoclinic KLu(WO4)2 crystal application of an intermediate configuration interaction theory. Opt. Mater. 2018, 78, 495–501. [Google Scholar] [CrossRef]
- Liu, G.K.; Carnall, W.T.; Jones, R.P.; Cone, R.L.; Huang, J. Electronic energy level structure of Tb3+ in LiYF4. J. Alloy. Compd. 1994, 207–208, 69–73. [Google Scholar] [CrossRef]
- Gusowski, M.A.; Ryba-Romanowski, W. Unusual behavior of Tb3+ in K3YF6 green-emitting phosphor. Opt. Lett. 2008, 33, 1786–1788. [Google Scholar] [CrossRef] [PubMed]
- Metz, P.W.; Marzahl, D.T.; Huber, G.; Kränkel, C. Performance and wavelength tuning of green emitting terbium lasers. Opt. Express 2017, 25, 5716. [Google Scholar] [CrossRef]
- Rajendra, H.J.; Pandurangappa, C.; Monika, D.L. Luminescence properties of dysprosium doped YVO4 phosphor. J. Rare Earths 2018, 36, 1245–1249. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, G.; Wang, J.; Dong, X.; Yu, W. Multicolor photoluminescence and energy transfer properties of dysprosium and europium-doped Gd2O3 phosphors. J. Alloy. Compd. 2015, 649, 96–103. [Google Scholar] [CrossRef]
- Rimbach, A.C.; Steudel, F.; Ahrens, B.; Schweizer, S. Tb3+, Eu3+, and Dy3+ doped lithium borate and lithium aluminoborate glass: Glass properties and photoluminescence quantum efficiency. J. Non Cryst. Solids 2018, 499, 380–386. [Google Scholar] [CrossRef]
- Perera, S.S.; Rabuffetti, F.A. Dysprosium-activated scheelite-type oxides as thermosensitive phosphors. J. Mater. Chem. C 2019, 7, 7601. [Google Scholar] [CrossRef]
- Nikolić, M.G.; Jovanović, D.J.; Dramićanin, M.D. Temperature dependence of emission and lifetime in Eu3+- and Dy3+-doped GdVO4. Appl. Opt. 2013, 52, 1716–1724. [Google Scholar] [CrossRef]
- Hertle, E.; Chepyga, L.; Batentschuk, M.; Will, S.; Zigan, L. Temperature-dependent luminescence characteristics of Dy3+ doped in various crystalline hosts. J. Lumin. 2018, 204, 64–74. [Google Scholar] [CrossRef]
- Bowman, S.R.; O’Connor, S.; Condon, N.J. Diode pumped yellow dysprosium lasers. Opt. Express 2012, 20, 12906–12911. [Google Scholar] [CrossRef] [PubMed]
- Haro-González, P.; Martín, L.L.; Martín, I.R.; Berkowski, M.; Ryba-Romanowski, W. Optical amplification properties of Dy3+-doped Gd2SiO5, Lu2SiO5 and YAl3(BO3)4 single crystals. Appl. Phys. B Lasers Opt. 2011, 103, 597–602. [Google Scholar] [CrossRef]
- Repelin, Y.; Husson, E.; Proust, F.B.C. Raman spectroscopy of lithium niobate and lithium tantalite. Force field calculations. J. Phys. Chem. Solids 1999, 60, 819–825. [Google Scholar] [CrossRef]
- Dominiak-Dzik, G. Sm3+-doped LiNbO3 crystal, optical properties and emission cross-sections. J. Alloy. Compd. 2005, 391, 26–32. [Google Scholar] [CrossRef]
- Dominiak-Dzik, G.; Ryba-Romanowski, W.; Palatnikov, M.N.; Sidorov, N.V.; Kalinnikov, V.T. Dysprosium-doped LiNbO3 crystal. Optical properties and effect of temperature on fluorescence dynamics. J. Mol. Struct. 2004, 704, 139–144. [Google Scholar] [CrossRef]
- Gryk, W.; Dyl, D.; Ryba-Romanowski, W.; Grinberg, M. Spectral properties of LiTaO3:Pr3+ under high hydrostatic pressure. J. Phys. Condens. Matter 2005, 17, 5381–5395. [Google Scholar] [CrossRef]
- Boutinaud, P. Rationalization of the Pr3+-to-transition metal charge transfer model: Application to the luminescence of Pr3+ in titano-nobates. J. Lumin. 2019, 214, 116557. [Google Scholar] [CrossRef]
- Englman, R.; Jortner, J. The energy gap law for radiationless transitions in large molecules. J. Mol. Phys. 1970, 18, 145. [Google Scholar] [CrossRef]
- Dorenbos, P.; Krumpel, A.H.; Boutinaud, E.v.P.; Bettinelli, M.; Cavalli, E. Lanthanide level location in transition metal complex compounds. Opt. Mater. 2010, 32, 1681–1685. [Google Scholar] [CrossRef]
- Dorenbos, P. Charge transfer bands in optical materials and related defect level location. Opt. Mater. 2017, 69, 8–22. [Google Scholar] [CrossRef]
- Nikl, M.; Morlotti, R.; Magro, C.; Bracco, R. Emission and storage properties of LiTaO3:Tb3+ phosphor. J. Appl. Phys. 1996, 79, 2853–2856. [Google Scholar] [CrossRef]
- Boutinaud, P.; Bettinelli, M.; Diaz, F. Intervalence charge transfer in Pr3+-and Tb3+-doped double tungstate crystals KRE(WO4)2 (RE = Y, Gd, Yb, Lu). Opt. Mater. 2010, 32, 1659–1663. [Google Scholar] [CrossRef]








| LiNbO3:Sm | LiNbO3:Dy | |
|---|---|---|
| Wnr (1/s) | 855 | 508 |
| Ea (cm−1) | 16,159 | 14,795 |
| α (cm−1/K) | 23.3 | 26.1 |
| ħω (cm−1) | 672 | 680 |
| Wr (1/s) | 1540 | 5164 |
| LiNbO3:Tb | LiTaO3:Tb | |
|---|---|---|
| Wnr (1/s) | 1064 | 807 |
| Ea (cm−1) | 1984 | 8128 |
| α (cm−1/K) | 17.1 | 17.6 |
| ħω (cm−1) | 693 | 778 |
| Wr (1/s) | 1874 | 1464 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lisiecki, R.; Macalik, B.; Kowalski, R.; Komar, J.; Ryba-Romanowski, W. Effect of Temperature on Luminescence of LiNbO3 Crystals Single-Doped with Sm3+, Tb3+, or Dy3+ Ions. Crystals 2020, 10, 1034. https://doi.org/10.3390/cryst10111034
Lisiecki R, Macalik B, Kowalski R, Komar J, Ryba-Romanowski W. Effect of Temperature on Luminescence of LiNbO3 Crystals Single-Doped with Sm3+, Tb3+, or Dy3+ Ions. Crystals. 2020; 10(11):1034. https://doi.org/10.3390/cryst10111034
Chicago/Turabian StyleLisiecki, Radosław, Bogusław Macalik, Robert Kowalski, Jarosław Komar, and Witold Ryba-Romanowski. 2020. "Effect of Temperature on Luminescence of LiNbO3 Crystals Single-Doped with Sm3+, Tb3+, or Dy3+ Ions" Crystals 10, no. 11: 1034. https://doi.org/10.3390/cryst10111034
APA StyleLisiecki, R., Macalik, B., Kowalski, R., Komar, J., & Ryba-Romanowski, W. (2020). Effect of Temperature on Luminescence of LiNbO3 Crystals Single-Doped with Sm3+, Tb3+, or Dy3+ Ions. Crystals, 10(11), 1034. https://doi.org/10.3390/cryst10111034