Effects of the Domain Wall Conductivity on the Domain Formation under AFM-Tip Voltages in Ion-Sliced LiNbO₃ Films

Abstract

The specified domain patterns were written by AFM-tip voltages in LiNbO₃ films composing LNOI (LiNbO₃-on-insulator). The domain wall conductivity (DWC) was estimated in the written patterns. This estimate was based on the effects of load resistors R_L inserted between DWs and the ground, on the features of occurring domains. In this case, the domain formation is controlled by the ratio between R_L and the DWs’ resistance R_DW. Starting from the comparison of patterns appearing at different R_L, the value of R_DW in a specified pattern was estimated. The corresponding DWC is of σ_DW ≈ 10⁻³ (Ohm cm)⁻¹ which exceeds the tabular bulk conductivity of LiNbO₃ by no less than twelve orders of magnitude. A small DW inclination angle of (10⁻⁴)⁰ responsible for this DWC is not caused by any external action and characterizes the domain frontal growth under an AFM-tip voltage.

1. Introduction

Ferroelectric materials have undergone a renaissance in the last two decades due to the discovery of many novel applications based on micro- and nanosized ferroelectric domains. The main examples of these applications are the nonlinear optical-frequency conversion [1] and an ultrahigh-density data storage [2]. More recently, interest has centered on the conductivity of charged domain walls (CDWs) which is a fundamental property of ferroelectric domains. The authors of [3] were the first to discuss the screening effects at the boundary of “encountering” (“head-to-head”) 180°-domains. The specificity of ferroelastic (twin) domain walls (DWs) was discussed in the pioneering works of Salje and co-authors, e.g., [4,5]. Particularly, the superconductivity at DWs in weakly reduced WO₃ and trapping of O-vacancies by DWs in CaTiO₃ was reported in [4] and [5], respectively. Later on, an enhanced domain-wall conductivity (DWC) up to the superconductivity was observed in a large amount of ferroelectric films and crystals; the detailed bibliography can be found in several reviews [6,7,8]. Taking into account a small DW thickness and a spatial mobility of ferroelectric domains, CDWs can be regarded as the field controlled nanosized wires. In the context of various applications, a concept of “DW nanoelectronics” was proposed by Catalan and coauthors [7].

DWC is caused by a DW inclination with respect to the direction of spontaneous polarization P_s and subsequent accumulation of a screening charge with the density of σ = 2P_s sinθ (where θ is the DWs’ inclination angle). The authors of [9] for the first time proved experimentally the relation of DWC to the DW inclination angle in LiNbO₃ crystals. In the recent TEM experiments [10], an essential meandering of 180° DWs has been found in PPLN, which predicts the appearance of DWC even at non-inclined DWs; for this case, the 2D resistor network approach was proposed [11].

The largest part of DWC studies were performed in LiNbO₃ [9,10,11,12,13,14,15], which is the most convenient object for these investigations not only because of its practical potentials, but due to the fact that domain patterns fabricated in this material by any technique, are stable.

The pioneering work [9] concerning the specified DWC in LiNbO₃ was mentioned above. The authors of [12] succeeded in enhancing DWC in LiNbO₃ by 3–4 orders of magnitude compared to [9], by means of the DWs’ field shaping in combination with a photoactive illumination. In [14] DWC was measured in the domain patterns with a specified DW inclination angle, written by AFM-tip voltages in LiNbO₃: 5% Mg plates.

The results described below were obtained in the domain patterns fabricated by AFM-tip voltages in LiNbO₃ films forming LNOI (LiNbO₃-on-insulator). For the further discussion, we dwell shortly on this device. The comprehensive bibliography can be found, e.g., in the reviews [8,16,17,18]. LNOI (schematically presented in Figure 1a) consists of an ion-sliced single-crystal single-domain LiNbO₃ film bonded on an insulating substrate (thin SiO₂ layer in our case); this sandwich is fixed onto a LiNbO₃ plate. In the LNOI samples under investigations, a thin metal layer serving as an electrode is inserted between LiNbO₃ film and SiO₂. Recently, we presented the AFM -tip domain writing in LiNbO₃ films forming LNOI [19,20] and DWC measurements in the written patterns [13]. Later on, AFM domain writing in LNOI and DWC observations in the written patterns were reported in [15,21,22].

According to the general concept, DWs represent regions of charge accumulation. As a result, an electrostatic repulsion between the closely spaced domains can be expected. Actually, some experimental data provide indirect evidence for this effect. When AFM domain writing in thin LiNbO₃ crystals, the neighboring domains became unstable [23] as the inter-domain distance Λ was reduced. Similarly, when AFM domain writing in He-LiNbO₃ optical waveguides, the domain sizes tended to decrease as Λ was decreased [24]. An instability and chaotic behavior observed in the domain patterns written by AFM-tip voltages in relatively thick LiNbO₃ films [25], can be attributed to an inter-domain electrostatic repulsion.

One can expect that an electrostatic repulsion should be suppressed by the DWs’ grounding leading to the elimination of accumulated charge. This effect was actually observed when AFM domain writing in LNOI [20]. If the metal layer was grounded when writing, the written patterns were regular and stable. Oppositely, if the metal layer was disconnected from the ground, the formed patterns were chaotic and unstable.

For clarity, the further reasoning underlying the problem setting is illustrated by Figure 1b. A domain pattern can be regarded as a system of conducting nanowires with a resistance R_DW, embedded into an insulating matrix. Two abovementioned extreme scenarios, namely, the regular and chaotic patterns occurring at R_L = 0 and R_L = ∞, can be interpreted as the results of grounding DWs and their disconnection from the ground, respectively.

The aim of the present research was to examine an “intermediate” case, namely, the domain formation in the conditions of R_DW grounding through a load resistor R_L ≠ 0 (Figure 1b). It was expected that the characteristics of the occurring domain patterns will be affected by R_L insertion, the effects being controlled by the ratio between R_DW and R_L.

Experiments were performed in LNOI samples provided by NANOLN Electronics (Jinan, China).

2. Experimental Results

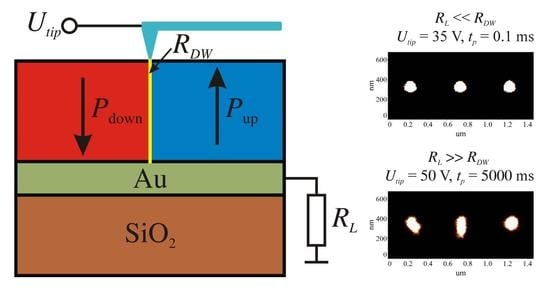
2.1. The Effects of R_L Insertion on the Domain Formation

The panels shown in Figure 2a–c, present the phase PFM images of the patterns written at different conditions. One can detect three types of scenarios, depending on the writing conditions.

Let us start from the writing at R_L = 0 (Figure 2a). In accordance with our recent results [19,20], domains appear on applying certain threshold U_tip. At U_tip lower than the threshold, no domains are detected obviously because of the backswitching.

In 500 nm thick films the threshold U_tip of the domain appearance is of 18 V; for thicker films it is somewhat larger. Figure 2a presents the results of writing at t_p = 0.1 ms, U_tip = 35 V. Qualitatively similar panels are visualized on writing in the ranges of U_tip > 22 V and t_p ≥ 0.1 ms (the shortest experimental t_p). The exposure characteristics of the domain diameter D(U_tip) and D(t_p) were presented in [19]. In agreement with [19,20], the written domains are fully stable. The dependences of the domain sizes D(U_tip) and D(t_p) are not affected by the inter-domain spacing. A specific feature of these patterns is the domain merging as the distance between the neighboring DWs is decreased (the upper rows in Figure 2a). This merging ignores the domain sizes and occurs when the distance between the neighboring DWs becomes lesser than 20–30 nm. The domain merging phenomenon was described in detail in our preceding publications [19,20].

We dwell shortly on the “pre-threshold” U_tip range from 18 to 22 V (Figure 2b) (R_L = 0). Figure 2b gives an example of panel written at U_tip = 20 V, t_p = 500 ms. The appearing domains are unstable since on turning-off U_tip, the domain diameter D is slowly shrinking during hours. At the smallest Λ = 100 nm (the upper row in Figure 2b) the domain sizes become somewhat irregular.

The insertion of load resistors R_L leads to the following results. Up to certain R_L value denoted below as R_crit, the scenario is very similar to that observed at R_L = 0, the writing conditions being the same (Figure 2a). At R_L > R_crit the writing characteristics change abruptly (Figure 2c). Now, to create a stable pattern with the domain sizes close to those observed at R_L = 0 under the same U_tip, the exposure time should be increased up to seconds, which exceeds t_p required for writing at 0 ≤ R_L ≤ R_crit more than by order of magnitude.

Let us discuss in order the phenomena described. In further consideration an ohmic contact between DWs and the metal layer was assumed.

A written pattern shorted to the metal layer, in its turn grounded through a resistor R_L can be represented jointly by an equivalent circuit consisting of two resistors, R_DW and R_L, connected in series (Figure 1b); here R_DW is the total DWs resistance. As the resistance of the surrounding crystal bulk is by orders of magnitude larger than R_DW, the voltage drop on it is neglected.

The phenomena occurring at R_L = 0 can be qualitatively accounted for by the elimination of an inter-domain repulsion due to the DW’s grounding. As a result, the times required for the formation of an equilibrium domain structure are rather short. Due to the disappearance of an inter-domain electrostatic repulsion, nothing prevents the domains from merging when they come together. The physical meaning of the critical distance of 20–30 nm between the neighboring DWs at which the domains start to merge, is unclear yet.

As follows from Figure 1b, at R_L≠ 0 the domain formation is governed by the ratio between R_L and R_DW. Provided that R_DW ≥ R_L, the voltage drop occurs mainly on R_DW; oppositely, in the case that R_L ≥ R_DW, the voltage drops dominantly on R_L. Therefore, in the latter case to write a pattern with the same characteristics as at R_L = 0, the exposure times should be increased essentially. This is actually observed in the case illustrated by Figure 2c. At U_tip = 35 V, R_L = 0 the exposure times of writing are of tenth of seconds, whereas when inserting R_L = 10¹⁰ Ohm, t_p becomes of the order of seconds.

In the framework of our consideration, a threshold change in the domain formation takes place at R_crit ≈ R_DW. In other words, at R_L = R_crit the voltage is divided approximately equally between R_L and R_DW. It should be taken into account (see the experimental procedure) that when writing any next panel, the value of R_L was changed by an order of magnitude. Due to this, the switch from the scenario illustrated by Figure 2a to that shown in Figure 2c occurs in a step-like manner. Therefore, for a given domain pattern, R_crit can be evaluated within an order of magnitude.

We dwell briefly on the domain formation in the “pre-threshold” voltage range Utip = 18–20 V (Figure 2b). The observed instability of domain patterns can be qualitatively accounted for by the fact that these voltages are insufficient to provide a complete grounding, so an inter-domain repulsion still persists. This qualitative explanation is supported by the fact that the threshold U_tip at which the writing characteristics change abruptly, grows with the film thickness being of 22 and 25 V for the 500 and 700 nm thick films, respectively. Note, an instability of AFM written domains in LNOI mentioned in [21], might be related to a non-complete grounding.

Summing up this section, a load resistor R_crit at which the results of writing change radically (from the panel 2a to 2c), is of the order of magnitude of DWs’ resistance R_DW. This approach paths the way to estimate R_DW in a given domain pattern by investigating the dependence of the occurring domain structures on the inserted resistors R_L.

The following remark is relevant here. Our consideration was illustrated by Figure 2a–c presenting the static ultimate structures. These structures result from the process, involving various stages, the slowest of which being obviously the screening of the bound charge by the free carriers. It occurs within a time of τ_M =εε₀/σ (where εε₀ and σ are the dielectric permittivity and conductivity, respectively). Taking the obtained below DW conductivity σ ≈ 2 × 10⁻⁷ (Ohm cm)⁻¹ and ε₃₃ ≈ 30 for LiNbO₃, we come to τ_M ≈ 10⁻⁷ s. Therefore, the final DWs’ equilibrium (static) state visualized by the PFM scanning is attained within the times by three orders shorter than the shortest exposure times t_p.

2.2. DWC Estimation Based on the Examination of Domain Patterns

A simplified reasoning presented above, paves the way to evaluate DWC in a given domain pattern. It can be done by investigating the effects of specified resistors R_L inserted between the metal layer and the ground, on the domain formation. In this section we present an example of this evaluation.

These experiments were performed by writing a row of circled domains by means of step-by-step AFM-tip movement. Figure 3a,b present, respectively, the amplitude PFM image of a fragment of this row and the scanline of an individual domain. The domains were written by U_tip = 27 V, t_p = 500 ms; the specified distance between the writing points was of Λ = 100 nm.

The sequence of these measurements was the same as when writing the domain panels discussed above. First, the domain row was written at R_L = 0 (the reference case). Then, the writing procedure was repeated with the inserted load resistors R_L ≠ 0, at each subsequent writing step R_L being raised by an order of magnitude. Up to R_L = 10⁹ Ohm the shape of the PFM image (illustrated by Figure 3a) remained almost unchanged. At R_L = 10¹⁰ Ohm a drastic change of the writing conditions was observed, namely to write a row identical to that shown in Figure 3a, tp should be increased up to several seconds, thus more than at ten times. In the framework of our consideration this jump takes place at R_L exceeding R_DW. Summing up, in the given pattern R_DW ≈ R_L = 10⁹ Ohm (correct to first order).

3. Discussion

This section consists of two parts. First, for the pattern shown in Figure 3, the DW conductivity σ_DW was calculated based on the above experimental estimate R_DW ≈ 10⁹ Ohm. Second, the DW inclination angle in the pattern shown in Figure 3 was evaluated in the framework of the approach proposed in [14].

3.1. DWC Calculations

Two independent approaches were used to calculate DWC. The first approach is as follows. A single domain can be represented by a cylinder with the diameter D; a DW is represented by a thin-walled tube with the wall thickness of w. The domains written by the U_tip amplitudes large enough, penetrate through the whole film thickness, thus the tube length is taken equal to the film thickness L. The resistance of a cylindrical domain with the DW thickness of w can be presented as:

R_DW = ρ_DW (L/πDw) ≡ 1/σ_DW (L/πDw)

(1)

As shown above, the conditions of the domain appearance change radically at certain load resistor R_crit. In the framework of our consideration it is equal to R_DW (correct to first order). From this it follows:

σ_DW = L/(πDwR_crit)

(2)

(for the notations see above).

All terms in this equation are specified except for the value of DW thickness w, which requires to be discussed in more detail. For different materials, e.g., BFO, BTO, and PZT, the value of w ≈ 10 nm was reported repeatedly (for references see [8]). In our measurements, to find this value, we used a tip with r ≤ 10 nm for the PFM scanning. This small tip radius permitted us to improve the accuracy of the DW’s thickness estimation. The repeated measurements in varied domain patterns analogous to that shown in Figure 3a, gave an average value of w ≈ 20 nm with the error of 10%. This value is in line with the literature data mentioned above [8].

Substituting R_crit = 10⁹ Ohm, L = 500 nm, D = 100 nm, w = 20 nm to Equation (2) we obtain σ_DW = 8 × 10⁻⁴ (Ohm cm)⁻¹. This estimate of DWC is conservative, since for DW thicknesses lesser than 20 nm, σ_DW would be larger.

We now turn to the alternative estimation of σ_DW, which is based on the approach proposed in [14]. The tip contact is considered as a point contact width d. The lines of the current density are curving and spreading out of the DW plane when moving away from the upper electrode. Then:

R_DW = ρ_DW (F/w) ≡ (1/σ_DW)(F/w)

(3)

where F is a dimensionless factor governed by the contact geometry; other notations see above. According to [14], the dependence of F on the contact geometry is satisfactorily approximated by a logarithmic function:

F = 0.72⋅lg(5L/a) ≈ 0.72⋅lg(5L/R_tip)

(4)

where a is the point contact width.

As was shown above, R_crit = R_DW. Taking into account Equation (4) we obtain:

σ_DW = F/(wR_crit) ≈ 0.72⋅lg(5L/R_tip)/(wR_crit)

(5)

Substituting into Equation (5) the values used above for calculations by Equation (2) (R_crit = 10⁹ Ohm, L = 500 nm, R_tip= 35 nm, w = 20 nm) we obtain σ_DW = 7 × 10⁻⁴ (Ohm cm)⁻¹. This is very close to the above alternative estimate σ_DW = 8 × 10⁻⁴ (Ohm cm)⁻¹. The value of σ_DW obtained by two methods exceeds the tabular bulk conductivity of LiNbO₃ not less than by twelve orders of magnitude.

3.2. The DW Inclination Angle

We now evaluate the DW inclination angle θ responsible for the σ_DW value estimated above. In these simplified calculations we follow [14]. The conductivity is expressed as σ = neµ, where n is the screening charge concentration, e is the elementary charge and µ is the charge mobility; so n = σ/eµ. Taking µ ≤ 10⁻² cm²/Vs and substituting it together with σ_DW ≈ 8 × 10⁻⁴ (Ohm cm)⁻¹ into the expression for the concentration of compensating electrons, we obtain n ≥ 0.6 × 10¹⁶ cm⁻³. The inclination angle θ required to provide this compensating charge is calculated from the expression new = 2P_s sinθ [14]. Substituting n ≥ 0.6 × 10¹⁶ cm⁻³, w = 20 nm and P_s = 70 µC cm⁻² to this expression, we obtain an inclination angle of θ ≈ (7 × 10⁻³)°. The validity of this estimate is supported by the results of [14], underlying our consideration. In that work, the calculations were performed for the angle θ ≈ 1° specified experimentally. As seen, the inclination of DWs in our case is by orders of magnitude lesser than the angles achieved with the aid of various experimental tricks (e.g., [9,12,14]). A negligible smallness of θ finds the following obvious explanation. As opposed to the aforementioned works aimed at rising DWC by increasing θ, in our case a domain was growing without any external action, so to say, “on its own”. Assuming the frontal DW motion to be the dominant mechanism of the domain growth, the DWs’ inclination angle is governed by the axial field distribution. So, the value of θ specified by the domain frontal growth itself, should be very small. Certain analogy can be drawn with the electron-beam EB domain writing in LiNbO₃ [26]. In that case the domains were growing axially under a local field created by EB-irradiation of the polar plane. The DWs in the formed domains appeared to be inclined by a very small angle.

4. Materials and Methods

The samples under study were LNOI wafers composed of a +Z-cut ion-sliced single-domain LiNbO₃ film bonded onto SiO₂ coated LiNbO₃ plate. The film thicknesses in the samples under study were of 300, 500 and 700 nm. The thickness of SiO₂ layers was of 1.4 µm. A 100 nm thick Au/Cr layer inserted between the bottom film surface and SiO₂ layer, served as an electrode. The total size of the samples was of X × Y × Z = (11 × 9 × 0.5) mm³.

The methods of the domain examination with the aid of scanning probe microscopy are commonly known, so needless to describe them in detail. The only detail should be mentioned. Two types of AFM tips were utilized for different aims. The domain writing and subsequent PFM scanning were performed using Si tip with Pt coating HA_FM/Pt (Tipsnano, Tallinn, Estonia) with the tip curvature radius R ≤ 35 nm. To determine the DWs’ thickness w in the written patterns, we used the Si tips with boron doped diamond coating HA_HR_DCP (Tipsnano) having a tip curvature radius R ≤ 10 nm. All AFM experiments were carried out with a NTEGRA PRIMA SPM system (NT–MDT, Moscow, Russia).

To search for the effects expected, the panels (illustrated by Figure 2) consisting of domain rows with the specified distances Λ between the writing points were written by the stepwise tip movement; in a given row Λ = const. On writing, each next panel was PFM–scanned. Any panel consisting of the domain rows with Λ decreasing from 1000 to 100 nm (bottom-up) was written under constant exposure conditions (U_tip = const, t_p = const).

When studying the effects of load resistors R_L ≠ 0 inserted between the metal layer and the ground on the domain occurrence, the sequence of operations was as follows. First, a reference panel was written under the given writing conditions (U_tip = const, t_p = const) at R_L = 0. Then, the following panels were written with the same U_tip and t_p, a load resistor R_L being inserted between LNOI and the ground. When writing each subsequent panel, the R_L value was increased (or decreased) by an order of magnitude. The domain panels written with R_L ≠ 0 were compared to the reference one.

The DWC measurements were performed in a row of circled domains written by step-by-step AFM-tip movement (Figure 3a,b). The sequence of these measurements was the same as when writing the domain panels (Figure 2). First, the domain row was written at R_L = 0 (the reference case). Then, the writing procedure was repeated with the inserted load resistors R_L ≠ 0. At each subsequent writing step, R_L was raised by an order of magnitude

5. Conclusions

The main results obtained here can be summarized as follows: The AFM-tip domain writing in LiNbO₃ films was investigated under various conditions of the DW’s grounding through the specified load resistors R_L inserted between DWs and the ground. The features of arising patterns are determined by the ratio between the domain-wall resistance R_DW and R_L. The formed patterns depend critically on R_L. This permitted us to estimate DWC in a specified pattern. Importantly, this estimate was based on the observations of ferroelectric phenomena. It was performed by comparing the patterns occurring at given Utip and tp with varied R_L. The calculations of DWC on the basis of two independent approaches gave the very close values of σ_DW = (7–8) × 10⁻⁴ (Ohm cm)⁻¹. In the framework of the approach developed in [14] this DWC corresponds to a small inclination angle of θ ≈ (7 × 10⁻³)°. The observed DWC not caused by any external manipulation, is related to a DW inclination accompanying the domain frontal growth under an AFM-tip field.

In our opinion, an important general conclusion is as follows: When creating a small-scale domain pattern, no matter by which method, an electrostatic repulsion between the neighboring DWs and, thus, the conditions of DWs’ grounding affect substantially the features of the occurring terminal domain structure.