Space-Selective Control of Functional Crystals by Femtosecond Laser: A Comparison between SrO-TiO2-SiO2 and Li2O-Nb2O5-SiO2 Glasses
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Samples
2.2. Laser Irradiation and Material Characterization
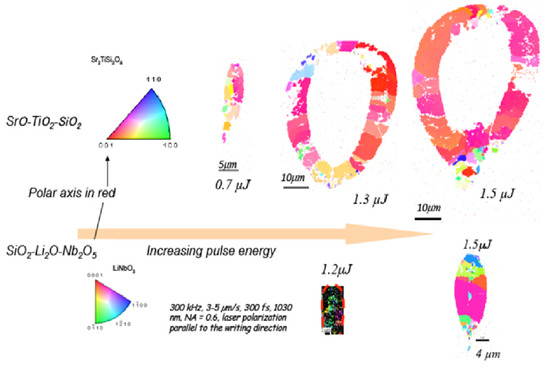
3. Results
- (1).
- At low pulse energy, the laser trace is completely crystallized in the Fresnoite system. The c-axis is rather well oriented in the direction of writing when the scanning speed is not too large, i.e., below a few μm/s.
- (2).
- Increasing the pulse energy, the size of the HAV increases dramatically and a crystallized shell surrounds an amorphous volume. In 3D, this defines an amorphous tube with crystallized walls. Again, the Fresnoite crystals are rather well oriented with c-axis aligned in the direction of beam scanning.
- (3).
- Increasing further the pulse energy (1.7 μJ at 20 μm/s or 1.5 μJ at 10 μm/s), the top of the tube is partially filled (see Figure 3g).
- (4).
- We note that the Fresnoite crystal texture with c-axis in the direction of scanning is deteriorated for large scanning speed (see Figure 3g).
- (5).
- At high energy but low speed, a SrTiO3 phase appears in the top of the HAV, mixed with Fresnoite and may reach about 50% of the volume.
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Choi, J.; Bellec, M.; Royon, A.; Bourhis, K.; Papon, G.; Cardinal, T.; Canioni, L.; Richardson, M. Three-dimensional direct femtosecond laser writing of second-order nonlinearities in glass. Opt. Lett. 2012, 37, 1029–1031. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Q.; Gan, F.; Zhao, X.; Tanaka, K.; Narazaki, A.; Hirao, K. Second-harmonic generation in Ge20As25S55 glass irradiated by an electron beam. Opt. Lett. 2001, 26, 1347–1349. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, Y.; Benino, Y.; Fujiwara, T.; Komatsu, T. Optical Second Order Nonlinearity of Transparent Ba2TiGe2O8 Crystallized Glasses. Appl. Phys. Lett. 2002, 81, 223. [Google Scholar] [CrossRef]
- Ochi, Y.; Meguro, T.; Kakegawa, K. Orientated crystallization of fresnoite glass-ceramics by using a thermal gradient. J. Eur. Ceram. Soc. 2006, 26, 627–630. [Google Scholar] [CrossRef]
- Ding, Y.; Masuda, N.; Miura, Y.; Osaka, A. Preparation of polar oriented Sr2TiSi2O8 films by surface crystallization of glass and second harmonic generation. J. Non-Cryst. Solids 1996, 203, 88–95. [Google Scholar] [CrossRef]
- Oikawa, T.; Honma, T.; Komatsu, T. Laser-induced crystal growth of nonlinear optical Ba3Ti3O6(BO3)2 on glass surface. Cryst. Res. Technol. 2008, 43, 1253–1257. [Google Scholar] [CrossRef]
- Komatsu, T.; Honma, T. Nucleation and Crystal Growth in Laser-Patterned Lines in Glasses. Front. Mater. 2016, 3. [Google Scholar] [CrossRef] [Green Version]
- Komatsu, T. Design and control of crystallization in oxide glasses. J. Non-Cryst. Solids 2015, 428, 156–175. [Google Scholar] [CrossRef]
- Miura, K.; Qiu, J.; Mitsuyu, T.; Hirao, K. Space-selective growth of frequency-conversion crystals in glasses with ultrashort infrared laser pulses. Opt. Lett. 2000, 25, 408–410. [Google Scholar] [CrossRef]
- Dai, Y.; Zhu, B.; Qiu, J.R.; Ma, H.L.; Lu, B.; Cao, S.X.; Yu, B.K. Direct writing three-dimensional Ba2TiSi2O8 crystalline pattern in glass with ultrashort pulse laser. Appl. Phys. Lett. 2007, 90, 181109. [Google Scholar] [CrossRef]
- Stone, A.; Jain, H.; Dierolf, V.; Sakakura, M.; Kashyap, R. Direct Laser-Writing of Ferroelectric Single-Crystal Waveguide Architectures in Glass for 3D Integrated Optics. Sci. Rep. 2015, 5, 10391. [Google Scholar] [CrossRef]
- Svaasand, L.O.; Eriksrud, M.; Nakken, G.; Grande, A.P. Solid-solution range of LiNbO3. J. Cryst. Growth 1974, 22, 230–232. [Google Scholar] [CrossRef]
- Cao, J.; Mazerolles, L.; Lancry, M.; Brisset, F.; Poumellec, B. Modifications in lithium niobium silicate glass by femtosecond laser direct writing: Morphology, crystallization, and nanostructure. J. Opt. Soc. Am. B 2017, 34, 160–168. [Google Scholar] [CrossRef]
- Fan, C. Contribution to Nano or Micro Crystallization Induction in Silica-Based Glass by Femtosecond Laser Irradiation. Ph.D. Thesis, Universite Paris-saclay, Orsay, France, 2012. [Google Scholar]
- Musgraves, J.D.; Richardson, K.; Jain, H. Laser-induced structural modification, its mechanisms, and applications in glassy optical materials. Opt. Mater. Express 2011, 1, 921–935. [Google Scholar] [CrossRef]
- Cao, J.; Lancry, M.; Brisset, F.; Mazerolles, L.; Saint-Martin, R.; Poumellec, B. Femtosecond Laser-Induced Crystallization in Glasses: Growth Dynamics for Orientable Nanostructure and Nanocrystallization. Cryst. Growth Des. 2019, 19, 2189–2205. [Google Scholar] [CrossRef]
- Cao, J.; Poumellec, B.; Brisset, F.; Helbert, A.L.; Lancry, M. Tunable angular-dependent second-harmonic generation in glass by controlling femtosecond laser polarization. J. Opt. Soc. Am. B 2016, 33, 741–747. [Google Scholar] [CrossRef]
- Wisniewski, W.; Thieme, K.; Rüssel, C. Fresnoite glass-ceramics—A review. Prog. Mater. Sci. 2018, 98, 68–107. [Google Scholar] [CrossRef]
- Lipat’ev, A.S.; Moiseev, I.A.; Lotarev, S.V.; Lipat’eva, T.O.; Presnyakov, M.Y.; Vasetskii, A.M.; Sigaev, V.N. Femtosecond Laser Assisted Local Crystallization of Barium-Titanate-Silicate Glass. Glass Ceram. 2018, 74, 423–427. [Google Scholar] [CrossRef]
- Höche, T.; Rüssel, C.; Neumann, W. Incommensurate modulations in Ba2TiSi2O8, Sr2TiSi2O8, and Ba2TiGe2O8. Solid State Commun. 1999, 110, 651–656. [Google Scholar] [CrossRef]
- Fokin, V.M.; Nascimento, M.L.F.; Zanotto, E.D. Correlation between maximum crystal growth rate and glass transition temperature of silicate glasses. J. Non-Cryst. Solids 2005, 351, 789–794. [Google Scholar] [CrossRef] [Green Version]
- Dai, Y.; Zhu, B.; Qiu, J.; Ma, H.; Lu, B.; Yu, B. Space-selective precipitation of functional crystals in glass by using a high repetition rate femtosecond laser. Chem. Phys. Lett. 2007, 443, 253–257. [Google Scholar] [CrossRef]
- He, X.; Poumellec, B.; Liu, Q.; Brisset, F.; Lancry, M. One-step photoinscription of asymmetrically oriented fresnoite-type crystals in glass by ultrafast laser. Opt. Lett. 2014, 39, 5423–5426. [Google Scholar] [CrossRef]
- He, X.; Fan, C.; Poumellec, B.; Liu, Q.; Zeng, H. Size-controlled oriented crystallization in SiO2-based glasses by femtosecond laser irradiation. J. Opt. Soc. Am. B 2014, 31, 376–381. [Google Scholar] [CrossRef]
- Ritland, H.N. Limitations of the Fictive Temperature Concept. J. Am. Ceram. Soc. 1956, 39, 403–406. [Google Scholar] [CrossRef]
- Poumellec, B.; Lancry, M.; Chahid-Erraji, A.; Kazansky, P.G. Modification thresholds in femtosecond laser processing of pure silica: Review of dependencies on laser parameters [Invited]. Opt. Mater. Express 2011, 1, 766–782. [Google Scholar] [CrossRef]
- Cao, J.; Poumellec, B.; Brisset, F.; Helbert, A.L.; Lancry, M. Angular Dependence of the Second Harmonic Generation Induced by Femtosecond Laser Irradiation in Silica-Based Glasses: Variation with Writing Speed and Pulse Energy. World J. Nano Sci. Eng. 2015, 5, 11. [Google Scholar] [CrossRef] [Green Version]
- Poumellec, B.; Lancry, M.; Desmarchelier, R.; Hervé, E.; Brisset, F.; Poulin, J.C. Asymmetric Orientational Writing in glass with femtosecond laser irradiation. Opt. Mater. Express 2013, 3, 1586–1599. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Tu, Z.; Du, X.; Zhang, H.; Qiu, J. Femtosecond laser induced migration of alkali ions in calcium silicate glasses. Mater. Lett. 2014, 137, 92–95. [Google Scholar] [CrossRef]
- Shimizu, M.; Sakakura, M.; Kanehira, S.; Nishi, M.; Miura, K. Formation Mechanism of Element Distribution in Glass Under Femtosecond Laser Irradiation. Opt. Lett. 2011, 36, 2161–2163. [Google Scholar] [CrossRef]
- Vogel, A.; Noack, J.; Hüttman, G.; Paltauf, G. Mechanisms of femtosecond laser nanosurgery of cells and tissues. Appl. Phys. B 2005, 81, 1015–1047. [Google Scholar] [CrossRef]
- Sanders, D.J. Temperature distributions produced by scanning Gaussian laser beams. Appl. Opt. 1984, 23, 30–35. [Google Scholar] [CrossRef]
- Miyamoto, I.; Horn, A.; Gottmann, J.; Wortmann, D.; Yoshino, F. Fusion Welding of Glass Using Femtosecond Laser Pulses with High-repetition Rates. J. Laser Micro Nanoeng. 2007, 2, 57–63. [Google Scholar] [CrossRef]
- Lax, M. Temperature rise induced by a laser beam. J. Appl. Phys. 1977, 48, 3919–3924. [Google Scholar] [CrossRef]
- Miyamoto, I.; Horn, A.; Gottmann, J. Local Melting of Glass Material and Its Application to Direct Fusion Welding by Ps-laser Pulses. J. Laser Micro Nanoeng. 2007, 2, 7–14. [Google Scholar] [CrossRef]
- Avramov, I.; Keding, R.; Rüssel, C. Crystallization kinetics and rigidity percolation in glass-forming melts. J. Non-Cryst. Solids 2000, 272, 147–153. [Google Scholar] [CrossRef]
- Wisniewski, W.; Patschger, M.; Russel, C. Sr-fresnoite surface crystallisation in a 2SrO center dot TiO2 center dot 2.75 SiO2 glass studied by EBSD. Crystengcomm 2012, 14, 5425–5433. [Google Scholar] [CrossRef]
- Cao, J.; Poumellec, B.; Brisset, F.; Lancry, M. Pulse energy dependence of refractive index change in lithium niobium silicate glass during femtosecond laser direct writing. Opt. Express 2018, 26, 7460–7474. [Google Scholar] [CrossRef]
- Stone, A.; Sakakura, M.; Shimotsuma, Y.; Miura, K.; Hirao, K.; Dierolf, V.; Jain, H. Femtosecond laser-writing of 3D crystal architecture in glass: Growth dynamics and morphological control. Mater. Des. 2018, 146, 228–238. [Google Scholar] [CrossRef]
- Inc. Chemical Catalog Company. Chemical Engineering Catalog, 12th ed.; The Chemical Catalog Company, Inc.: New York, NY, USA, 1927. [Google Scholar]
- Fang, Z.; Xiao, X.; Wang, X.; Ma, Z.; Lewis, E.; Farrell, G.; Wang, P.; Ren, J.; Guo, H.; Qiu, J. Glass-ceramic optical fiber containing Ba2TiSi2O8 nanocrystals for frequency conversion of lasers. Sci. Rep. 2017, 7, 44456. [Google Scholar] [CrossRef]
- Kingery, W.D. Thermal Conductivity: XII, Temperature Dependence of Conductivity for Single-Phase Ceramics. J. Am. Ceram. Soc. 1955, 38, 251–255. [Google Scholar] [CrossRef]
- Morgan, R.A.; Kang, K.I.; Hsu, C.C.; Koliopoulos, C.L.; Peyghambarian, N. Measurement of the thermal diffusivity of nonlinear anisotropic crystals using optical interferometry. Appl. Opt. 1987, 26, 5266–5271. [Google Scholar] [CrossRef] [PubMed]
- Vigouroux, H. Etude de Vitrocéramiques Optiques Pour le Doublement de Fréquence; University of Bordeaux: Bordeaux, France, 2012. [Google Scholar]
- Shimada, M.; Honma, T.; Komatsu, T. Laser patterning of oriented LiNbO3 crystal particle arrays in NiO-doped lithium niobium silicate glasses. Int. J. Appl. Glass Sci. 2018, 9, 518–529. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Xu, X.; Yu, G.; Wang, N. Electronic Structures and Pr3+ Photoluminescence Characteristics in Fresnoite, Sr-Frenoite, and Ge-Frenoite. J. Am. Ceram. Soc. 2011, 94, 496–500. [Google Scholar] [CrossRef]
- Thierfelder, C.; Sanna, S.; Schindlmayr, A.; Schmidt, W. Do we know the band gap of lithium niobate? Phys. Status Solidi 2010, 7, 362–365. [Google Scholar] [CrossRef]
- Yonesaki, Y.; Kiyotaka, M.; Ryuhei, A.; Koji, F.; Kazuyuki, H. Space-selective precipitation of non-linear optical crystals inside silicate glasses using near-infrared femtosecond laser. J. Non-Cryst. Solids 2005, 351, 885–892. [Google Scholar] [CrossRef]
- Shimotsuma, Y.; Kazansky, P.G.; Qiu, J.R.; Hirao, K. Self-organized nanogratings in glass irradiated by ultrashort light pulses. Phys. Rev. Lett. 2003, 91, 247405. [Google Scholar] [CrossRef] [Green Version]
- Shimotsuma, Y.; Sakakura, M.; Miura, K. Photoinduced self-assembly of nanostructure. In Proceedings of the 77th JSAP Autumn Meeting, Niigata city, Japan, 13–16 September 2016; pp. 301–307. [Google Scholar]
- Cao, J.; Poumellec, B.; Mazerolles, L.; Brisset, F.; Helbert, A.L.; Surble, S.; He, X.; Lancry, M. Nanoscale Phase Separation in Lithium Niobium Silicate Glass by Femtosecond Laser Irradiation. J. Am. Ceram. Soc. 2017, 100, 115–124. [Google Scholar] [CrossRef] [Green Version]
- Höche, T.; Neumann, W.; Esmaeilzadeh, S.; Uecker, R.; Lentzen, M.; Rüssel, C. The Crystal Structure of Sr2TiSi2O8. J. Solid. State. Chem. 2002, 166, 15–23. [Google Scholar] [CrossRef]
- Halliyal, A.; Safari, S.; Bhalla, R.; Newnham, E.; Cross, L. Grain-Oriented Glass-Ceramics for Piezoelectric Devices. J. Am. Ceram. Soc. 1984, 67, 331–335. [Google Scholar] [CrossRef]








| STS Glass | LNS Glass | Ref. | |
|---|---|---|---|
| Heat capacity Cp | 410 J·kg−1·K−1 | 650 J·kg−1·K−1 | [18,40] |
| Specific mass ρ | 3887 kg/m3 | 3830 kg/m3 | [41] and interpolation |
| Thermal conductivity κ | 10.1 J/Kms | 2.65 J/Kms | Deduced from diffusivity |
| Thermal diffusivity DT | 70 × 10−7 m2/s | 9 × 10−7 m2/s | Interpolated from [42,43] |
| Melting Tm (°C) | Sr-Fresnoite = 1312 | LiNbO3 = 1257 | [36,44] |
| Glass temp. Tg (°C) | 760 | 551 | [18,45] |
| Bandgap (eV) | 5.1 | 3.7–4.7 | [46,47] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Liu, Q.; Lancry, M.; Brisset, F.; Poumellec, B. Space-Selective Control of Functional Crystals by Femtosecond Laser: A Comparison between SrO-TiO2-SiO2 and Li2O-Nb2O5-SiO2 Glasses. Crystals 2020, 10, 979. https://doi.org/10.3390/cryst10110979
He X, Liu Q, Lancry M, Brisset F, Poumellec B. Space-Selective Control of Functional Crystals by Femtosecond Laser: A Comparison between SrO-TiO2-SiO2 and Li2O-Nb2O5-SiO2 Glasses. Crystals. 2020; 10(11):979. https://doi.org/10.3390/cryst10110979
Chicago/Turabian StyleHe, Xuan, Qiming Liu, Matthieu Lancry, François Brisset, and Bertrand Poumellec. 2020. "Space-Selective Control of Functional Crystals by Femtosecond Laser: A Comparison between SrO-TiO2-SiO2 and Li2O-Nb2O5-SiO2 Glasses" Crystals 10, no. 11: 979. https://doi.org/10.3390/cryst10110979
APA StyleHe, X., Liu, Q., Lancry, M., Brisset, F., & Poumellec, B. (2020). Space-Selective Control of Functional Crystals by Femtosecond Laser: A Comparison between SrO-TiO2-SiO2 and Li2O-Nb2O5-SiO2 Glasses. Crystals, 10(11), 979. https://doi.org/10.3390/cryst10110979