Determination of Long-Range Internal Stresses in Cyclically Deformed Copper Single Crystals Using Convergent Beam Electron Diffraction

Abstract

Understanding long range internal stresses (LRIS) may be crucial for elucidating the basis of the Bauschinger effect, plastic deformation in fatigued metals, and plastic deformation in general. Few studies have evaluated LRIS using convergent beam electron diffraction (CBED) in cyclically deformed single crystals oriented in single slip and there are no such studies carried out on cyclically deformed single crystals in multiple slip. In our earlier and recent study, we assessed the LRIS in a cyclically deformed copper single crystal in multiple slip via measuring the maximum dislocation dipole heights. Nearly equal maximum dipole heights in the high dislocation density walls and low dislocation density channels suggested a uniform stress state across the labyrinth microstructure. Here, we evaluate the LRIS by determining the lattice parameter in the channels and walls of the labyrinth dislocation structure using CBED. Findings of this work show that lattice parameters obtained were almost equal near the walls and within the channels. Thus, a homogenous stress state within the heterogeneous dislocation microstructure is again suggested. Although the changes in the lattice parameter in the channels are minimal (less than 10⁻⁴ nm), CBED chi-squared analysis suggests that the difference between the lattice parameter values of the cyclically deformed and unstrained copper are slightly higher in the proximity of the walls in comparison with the channel interior. These values are less than 6.5% of the applied stress. It can be concluded that the dominant characteristics of the Bauschinger effect may need to include the Orowan-Sleeswyk mechanism type of explanation since both the maximum dipole height measurements and the lattice parameter assessment through CBED analysis suggest a homogenous stress state. This work complements our earlier work that determined LRIS based on dipole heights by assessing LRIS through a different methodology, carried out on a cyclically deformed copper single crystal oriented for multiple slip.

1. Introduction

The concept of LRIS in metals refers to the deviation of local stress from the applied stress that occurs over relatively long length scales such as that of the spacing of dislocation heterogeneities (e.g. labyrinth microstructure [1], persistent slip bands (PSB) walls, cell walls, subgrain boundaries, etc). LRIS may have been initially discussed in connection with the Bauschinger effect [2]. Understanding LRIS is essential for characterizing the Bauschinger effect and plastic deformation in cyclically deformed metals [3,4]. Metals strain harden during plastic deformation and upon reversal of the applied stress, yielding occurs at a much lower (absolute value) stress than if the material continued monotonic deformation. This effect is referred to as the Bauschinger effect and is contrary to what is expected based on isotropic hardening. When a metal is cyclically deformed, the lost strength due to the Bauschinger effect occurs with each reversal of the applied stress. This results in low hardening rates and saturation stresses compared to the (monotonic) fracture stress [3]. Different theories have been proposed for rationalizing the Bauschinger effect [5,6,7,8]. The two prominent theories are Mughrabi’s composite model [5], which proposed relatively high values of LRIS, and the Orowan-type mechanism [6], which involves no internal stresses.

The Mughrabi composite model presented the heterogenous dislocation microstructure as hard (high dislocation density walls) and soft (low dislocation density channels or cell interiors) sections. In the forward direction of deformation (tension), the stress is positive in both the walls and channels (hard and soft regions). However, in the reverse direction of deformation (compression), while the stress in the walls are still positive, these regions can place the cell interiors, PSB channels, etc. in compression. Thus, the Bauschinger effect, which is the occurrence of yielding at lower stresses, is observed in this simplified model [2].

The Orowan-type mechanism, which was discussed in more details by Brown in [9,10], suggests that mobile dislocations in the forward direction of straining encounter an increasing lineal density of obstacles (forest dislocations or dislocation walls). However, in the reverse direction, there is a lower lineal density of obstacles (channels or cells interiors). Therefore, plastic strains are accumulated at a much lower stresses on reversal [6,7].

Historic LRIS assessment studies on high dislocation density heterogeneities of cyclically deformed single crystals oriented for single slip suggest internal stresses in the so-called hard phase varying from a factor of 1.0 (no LRIS) to 3, or more (larger than the applied stress). These studies were based on measurements of dislocation dipole height, dislocation loop radii, asymmetry in X-ray peaks, and lattice parameter measurements through CBED analysis [5,11,12,13,14,15,16,17,18,19]. In an earlier recent study by the authors [1], the maximum dipole heights were discovered to be approximately independent of location, being almost identical in the walls and channels of the labyrinth dislocation microstructure in <001> Cu single crystals oriented for multiple slip. Since the maximum dipole height strength values may be indicative of the local stresses, nearly equal maximum dipole heights in the walls and channels support a uniform stress state and low LRIS. However, the maximum value for dipole heights suggest dipole strengths that were about a factor of 2.4 higher than the applied stress based on the usual athermal equation to separate the dislocations of a dipole. Extra stress at the dipoles may be provided by tripoles or small dislocation pile-ups [20]. A nearly homogenous stress distribution with only small internal stresses were suggested by the authors in an earlier study [1] to be present based on the maximum dipole separation stress values. This is consistent with the observation of uniform dipole height across the heterogeneous dislocation microstructure. Other studies reported similar behaviors, observing homogenous dipole heights and higher dipole separation stresses for cyclically deformed metal single crystals oriented in single slip (except aluminum, which has a similar dipole separation stress to the applied stress but homogenous dipole heights as usual) [11,12,13]. It should be noted that accounting on either the anisotropy of cubic elasticity or the finite elongation ratios of dipoles did not allow the authors to explain the aluminum specificity. As stated earlier, since the maximum dipole heights are the upper limit of stable dipoles under the imposed local stress, they can predict the local stresses in cyclically deformed materials. The local stresses may be more accurately measured by determining the lattice parameters using convergent beam electron diffraction. This method involves using a small convergent electron probe to generate a diffraction pattern containing the higher order Laue zone (HOLZ) lines that are very sensitive to small elastic distortions in the lattice.

There have been few studies on internal stress assessment using the CBED technique in creep deformed and fatigued polycrystals and single crystals oriented in single slip. Such studies on cyclically deformed single crystals oriented in multiple slip are missing in the literature. Straub et al. [21] and Maier et al. [22] examined internal stresses using CBED analysis in polycrystalline copper specimens experiencing either creep or cyclic deformation. They did not quantify the internal stresses but suggested that internal stresses exist. It should be noted that both of these studies used kinematical simulations for deriving the position of the HOLZ lines, but dynamical effects may be important. Kassner et al. observed a homogenous stress distribution with no internal stresses in an unloaded monotonically (creep deformed) polycrystalline copper using CBED analysis [23]. In another CBED study by Kassner et al., an absence of internal stresses in creep deformed aluminum single crystal was reported [24]. In the most recent study by Kassner et al. on a cyclically deformed copper single crystal oriented for single slip at ambient temperature, lattice parameter measurements in the channels and close to the vein bundles showed no evidence of LRIS. The uncertainty of these measurements was ±30 MPa, which is 80% of their applied stress [25]. Furthermore, it was not determined whether relaxation occurred leading to a reduction in the LRIS. Legros et al. [26] assessed the internal stresses in a cyclically deformed silicon single crystal oriented for single slip at 1078 K using chi-squared analysis on CBED patterns. Chi-squared is the typical refinement method for producing the best match between the simulated and experimental CBED patterns [27]. Legros et al. suggested small internal stresses closer to the dislocation wall (7 MPa or about 14% of their applied stress) and negligible internal stresses within the cell interior exist in the cyclically deformed silicon single crystal [26]. This is basically consistent with the earlier work by the authors of this paper on the structures without PSBs. Again, all of the studies in the literature that use CBED for strain measurements were performed on unloaded material, and, of course, examined on the thin regions of the foil. Thus, LRIS relaxation is possible.

In this study, we evaluated the lattice parameters using CBED in the channels and close to the walls of the labyrinth microstructure of a cyclically deformed copper <001> single crystal oriented in multiple slip which complements the dipole study of our earlier work [1].

2. Materials and Methods

Copper single crystals of 99.999% purity oriented in [001], were cyclically deformed in tension/compression at room temperature to 157 cycles at a strain amplitude of 4.0 × 10⁻³ and a strain rate of 2 × 10⁻³ s⁻¹. This single crystal copper was cyclically deformed in multiple slip with 8 active slip systems of identical Schmid factor of 0.408. Figure 1a illustrates the stress versus strain behavior of the cyclically deformed specimen. Figure 1b illustrates that the copper single crystal was fatigued to saturation to an axial stress of 275 MPa (a resolved shear stress of 112 MPa in the <110> direction on a {111} plane). A deceleration in the cyclic hardening rate up to the maximum peak stress at the 108th cycle followed by a very slow softening until the 157th cycle was observed. The specimens were stored in a liquid nitrogen container to suppress recovery and recrystallization subsequent to deformation, which has been observed in other high purity metals [28,29]. TEM disks from the (100), (001), and (010) planes were prepared using conventional jet electropolishing with a Fischione twin jet (Fischione Instruments Inc., Export, PA, USA). Foil preparation details can be found in earlier publication by the authors [1]. Figure 1a shows that the macroscopic back stress is about one half of the maximum stress, independent from the number of cycles (a few cycles: no labyrinth structure versus about 80 cycles close to the quasi-saturation stage, considered as the labyrinth domain).

CBED studies were done on both the cyclically deformed copper and a 99.999% pure unstrained copper using the JEOL JEM-2100F transmission electron microscope (TEM) (JEOL Inc., Peabody, MA, USA) at the University of Southern California at an accelerating voltage of 200 kV and a beam diameter of about 40 nm. In order to obtain the lattice parameter from CBED patterns, comparisons between the experimental CBED patterns with simulated ones were made [27]. In this study the EMSOFT codes that consider a dynamical behavior of the electrons within the specimen were used for CBED patterns simulations [30].

Figure 2 illustrates the 3-dimensional microstructure based on TEM images taken from the (100), (010), and (001) planes of the cyclically deformed copper [1]. The stress axis is parallel to the vertical [001] direction. The heterogeneous labyrinth dislocation microstructure consisting of orthogonal high dislocation density walls and low dislocation density channels is observed. Dislocation density in the walls and channels of the labyrinth structure was 8.6 × 10¹⁴ m/m³ and 1.55 × 10¹³ m/m³ respectively [1].

Figure 3 illustrates TEM micrographs of the labyrinth structure viewing from the [010] direction. All the dipole height measurements [1] and CBED analysis were performed on the labyrinth structure on the (010) planes.

3. Results and Discussion

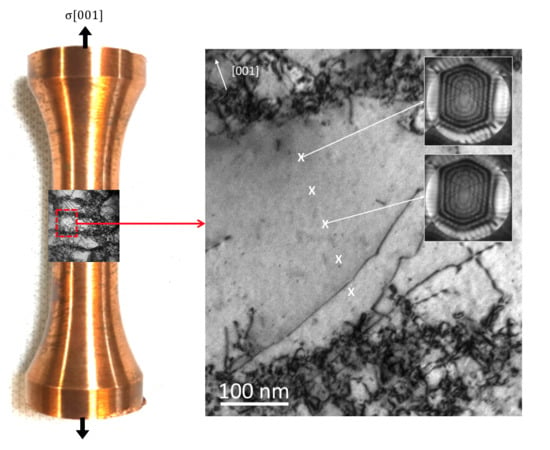
Strain determination is based on the shifts of the HOLZ lines in the strained specimen relative to the unstrained pattern. Specific orientations are more sensitive to the changes in the strain state. The <411> zone axis has been shown to be highly sensitive to changes in strain of face centered cubic (FCC) crystals [31]. The <411> CBED patterns were acquired in small volumes of the cyclically deformed copper very close to and remote from a dislocation heterogeneity (dislocation walls) and in the direction of applied stress ([001]). A channel with five locations where a CBED pattern was acquired is illustrated in Figure 4. The closest a CBED pattern could be acquired from a dislocation heterogeneity was approximately 30 nm. Below 30 nm, the dislocation tangles within the walls are too close to the electron probe, causing perturbations within the CBED pattern.

Lattice parameter determination was performed using the normalized distance between different HOLZ line intersections. Normalization by using the ratios of the distance between different intersections was used to adjust for differences in magnification. The comparison of simulated and experimental patterns is achieved by using the chi-squared equation, which is the typical refinement method for producing the best match between the simulated and experimental patterns [27]. The chi-squared equation is defined as:

$${\chi }^2={\displaystyle \sum }_i^N\frac{1}{d_{is}}{\left(d_{is}-d_{ix}\right)}^2$$

(1)

where N is the number of data points, d_s is the normalized distance between two intersections in the simulated pattern, and d_x is the normalized distance between the same intersections of the experimental pattern. As stated earlier, the CBED pattern of an unstrained copper single crystal has also been recorded and compared with the simulated patterns to determine the observed lattice parameter of the undeformed copper. Consequently, the strain can be evaluated by comparing the lattice parameter of the cyclically deformed copper with the unstrained value. The strain was converted into stress using the elastic modulus along the [001] direction E [001] = 66.6 ± 0.5 GPa [32], accounting for the cubic elasticity anisotropy of copper.

Figure 5 shows the lattice parameter measurements and stress calculations corresponding to different positions within the channel. The data are obtained from four channels in two TEM foils. The horizontal axis shows the distance from the walls normalized by the channel width. The average channel width is 0.36 μm and the wall width is about 0.12 μm. Minor scatterings exist in the lattice parameters of different channels that is ±2 × 10⁻⁴ nm. Identical values of lattice parameters in each channel show that the internal stresses are homogenous in the channel and close to the walls of the labyrinth dislocation microstructure. Comparing the lattice parameter of cyclically deformed copper single crystal with that of unstrained copper indicates that the internal stresses are minimal. Considering Brown’s note on permanent softening, this weak backstress is in line with the fact that the measured cyclic softening in our test was weak [9,10]. Of course, it is possible that internal stresses exist and are less than the measurement error. The accuracy of lattice parameter measurements is about ±1 × 10⁻⁴ nm. The error in stress measurements is then approximately ±18 MPa that is 6.5% of the applied axial stress of 275 MPa.

Following the Legros et al. [26] method of chi-squared analysis, an effort was made to assess the local changes of the lattice parameter within a single channel. Since the lattice parameter of the unstrained copper was observed to be 0.3592 nm, channel four with the lattice parameter of 0.3592 nm in the cyclically deformed copper was chosen for this analysis. HOLZ lines of simulated CBED patterns corresponding to the lattice parameter of 0.35920 nm were considered as the reference point for chi-squared analysis. The data illustrated in Figure 6 is a chi-squared fit between the aforementioned HOLZ lines intersection ratios for cyclically deformed (yellow) and undeformed (red) copper. Chi-squared analysis can “refine” the strain measurement below 10⁻⁴ and provide increased resolution of the elastic strain, although precise values of the strain within in the 10⁻⁵ range is not possible. The chi-squared results plotted in Figure 6 are somewhat qualitative. Although the changes in the lattice parameter in a channel are minimal and less than 1 × 10⁻⁴ nm, the data shown in Figure 6 can show that the difference between the lattice parameter values of the cyclically deformed copper and the unstrained copper are slightly higher in the proximity of the walls in comparison with the values in the channel interior. This result is consistent with the composite model but with much lower values of internal stresses (less than 6.5% of the applied stress). It should also be noted that the aforementioned differences in the chi-squared values might be due to the higher quality of HOLZ lines in the middle of the channels as opposed to the vicinity of the walls. Considering the two renowned theories that rationalize the Bauschinger effect (Composite model and Orowan-Sleeswyk mechanism), it appears that the dominant characteristics of the Bauschinger effect may need to include the Orowan–Sleeswyk [6] mechanism type of explanation since both the maximum dipole height measurements and the lattice parameter assessment through CBED analysis suggest a relatively homogenous stress state. As stated earlier, no internal stresses are involved in the Orowan-Sleeswyk mechanism where the Bauschinger effect is rationalized by the lower lineal density of obstacles in reverse direction of straining.

It should be noted that dislocations may eject out of the surface in the thin areas of the TEM foil. This will result in stress relaxation and can subsequently alter the values of the internal stress. This is rather challenging since thin areas of the specimen are to be used for acquiring high quality HOLZ lines in a CBED pattern. It must be emphasized that these relaxations may be negligible as the labyrinth pattern with similar characteristics such as dislocation density, channel, and wall width were observed both in the thin regions as well as thicker areas. The dislocation density in the thinner regions (approximately 130 ± 10 nm) where CBED patterns were recorded was 8.2 × 10¹⁴ m/m³ in the walls and 1.8 × 10¹³ m/m³ in the channels. This is very close to the wall dislocation density of 8.6 × 10¹⁴ m/m³ and channel dislocation density of 1.5 × 10¹³ m/m³ in relatively thicker regions (approximately 0.23 $\mathsf{\mu }\mathrm{m}$) where dislocation densities were measured [1]. Although copper has a fairly low stacking fault energy of 60 mJ/m² and the labyrinth microstructure characteristics including dislocation densities are consistent in the thick and thin regions, relaxations caused by dislocations ejecting the thin regions of the foil cannot be completely neglected.

As stated earlier, there have been few studies on internal stress assessment using the CBED technique in creep deformed and fatigued polycrystals and single crystals oriented in single slip. Such studies on cyclically deformed single crystals oriented in multiple slip are missing in the literature. The current study shows a uniform stress state within the crystal since the lattice parameters are almost identical near the dislocation walls and within the channel. This is similar to the findings of earlier studies on fatigued copper and silicon oriented for single slip and creep deformed aluminum and copper [21,22,23,24,25,26]. All of the deformation conditions of the current study along with other studies that used CBED to assess LRIS are summarized in

Table 1. Summary of studies on creep and cyclically deformed materials that utilized CBED to assess long range internal stresses.

CBED Studies	This Study	Kassner [25]	Legros [26]	Kassner [24]	Kassner [23]		Straub [21]	Maier [22]
Material	Copper [001] Single Crystal	Copper [123] Single Crystal	Silicon [231] Single Crystal	Aluminum Single Crystal	Copper Polycrystal		Copper Polycrystal	Copper Polycrystal
Deformation Type	Cyclic	Cyclic	Cyclic	Creep Steady State	Creep Steady State		Creep	Cyclic
Applied Stress (MPa)	112 (Shear) Saturation	19 (Shear) Presaturation	49 (Shear) Presaturation	7 (Axial)	20	40	162 (Axial)	144 (Axial)
					(Axial)
Strain	0.40%	0.125% Plastic only	6 × 10−4 Plastic only	-	0.04	0.05	3.6	5 × 10−3 Plastic only
Strain Rate (s−1)	2 × 10−3	2.5 × 10−3	3 × 10−4	-	2.5 × 10−5	5.6 × 10−7	1.9 × 10−3	-
Slip	Polyslip	Single Slip	Single Slip	-	-		-	-
Number of Cycles	157	200	-	-	-		-	2000
Temperature (K)	293	293	1078	663	823		573	293
LRIS	None	None	None	None	None		Observed	Observed

.

4. Conclusions

The lattice parameter assessment through convergent beam electron diffraction patterns recorded in the channels and close to the walls of the labyrinth dislocation structure suggest very low long range internal stresses (LRIS). Our earlier dipole height work on the same cyclically deformed copper also suggests low internal stresses. The stress to separate dipoles with the widest height was independent of the location. Therefore, the results of the current CBED analysis study is consistent with our earlier maximum dipole height measurement work.

Minimal changes (less than 10⁻⁴ nm) were observed in the lattice parameters recorded throughout a single channel. These values are less than 6.5% of the applied stress. Hence, negligible internal stresses in the channel interior and near the dislocation walls were observed. The Kassner et al. X-ray synchrotron study on monotonically deformed (to 30% strain at ambient temperature) copper single crystals [32] suggest that long range internal stresses were nearly 10% of the applied stress. Thus, the outcome of the present cyclic deformation study is consistent with the earlier monotonic deformation work. Although the changes in the lattice parameter in a channel are very minimal (less than 10⁻⁴ nm), chi-squared analysis suggest that the difference between the lattice parameter values of the cyclically deformed copper and the unstrained copper are slightly higher in the proximity of the walls in comparison with the channel interior. These internal stresses are less than 6.5% of the applied stress. This is consistent with the composite model originally suggested by Mughrabi but with perhaps lower values of internal stresses. Therefore, it appears that a low proportion of the Bauschinger effect may be influenced by the existence of long range internal stresses. The dominant feature of the Bauschinger effect may include the Orowan–Sleeswyk [6] mechanism type of explanation, since both the maximum dipole height measurements and the lattice parameter assessment through CBED analysis suggest a relatively homogenous stress state within the heterogeneous dislocation microstructure.