2.1. 31P NMR of LDP
In the solid state, the NMR response of a spin
nucleus such as
31P is governed by the chemical shift (CS), and by dipolar (direct) couplings between spins [
3]. In the LiH
PO
lattice, the dipolar couplings between the nuclear spins result in homogeneous line broadening only (as discussed in more detail below), and will not be quantitatively evaluated here. The resonance frequency
of
P in LDP may thus be described by the following general notation:
Here,
is the Larmor frequency which scales with the magnetic field strength, and
the contribution of the chemical shift which is gauged by the chemical shift tensor
. Generally, for NMR spectroscopy of single crystals, it is useful to define three distinct coordinate systems, i.e., the laboratory frame, where the
z axis is defined by the orientation of the external magnetic field, the crystal lattice (
) frame and the principal axis system (
). In the orthorhombic unit cell of LDP, the four phosphorus (and lithium) atoms at Wyckoff position
are related by a two-fold rotation axis parallel to the crystallographic
c axis and two glides parallel to the
, and
plane. Since NMR is invariant to translational elements and inversions, one can trace four
P atoms in the single-crystal spectra (see
Figure 1c), which are related by 180° rotations about the three crystallographic
axes, starting from the atom closest to the unit cell origin:
Their respective CS tensors in the orthorhombic
frame are therefore described by six independent tensor components which differ only by sign for each
P position:
To quantitatively determine these chemical shift tensors, a single crystal of LDP with approximate dimensions of
mm
grown from solution (see Experimental) was fixed on a wooden rotation axis as depicted in
Figure 1a. In the goniometer setup, this rotation axis is oriented perpendicular to the external magnetic field. The line positions observed in the
P NMR spectrum depend on the relative orientation of the magnetic field vector
to the
tensor in the crystal frame, and, in ppm, are given by [
9,
10]:
P-NMR spectra of the LDP crystal were recorded in steps of 10°, some of which are shown in
Figure 2a. Plotting the resonance position for each phosphorus atom over a 180° interval, as depicted in
Figure 2b, results in a so-called ‘rotation pattern’. The contribution of each magnetically inequivalent
P(
n) atom, with
, in these rotation pattern follows the type of harmonic function shown in Equation (
4), which is defined by the three factors
,
, and
. These factors are linear combinations of the CS tensor components and depend on the relative orientation of
to the
frame. The step-wise movement of
by angle
in the orthorhombic crystal frame may be written as:
Here,
and
are auxiliary unit vectors in the plane perpendicular to the (initially unknown) rotation axis
. To unequivocally set
,
, and the offset angle
, a reference vector perpendicular to
is needed. For our data, we chose the crystallographic
c axis as a reference vector, with the calculation details shown in reference [
11]. For one physical rotation axis
, the four harmonics in the
P rotation pattern are linked by one constraint to one another [
12]. Hence,
linear independent parameters may be extracted from fitting the data of one rotation pattern. The chemical shift tensor we want to obtain possesses six independent components according to Equation (
3). Adding the two angles
and
defining the orientation of the rotation axis in the
frame, and the offset angle
, a total of nine fit parameters need to be extracted from the NMR data. Thus, in principle, one rotation pattern (such as the one shown in
Figure 2b) encapsulates sufficient information to determine the
P CS tensor in LDP, together with the orientation of the rotation axis and the offset angle.
However, as may be seen in the single-crystal spectra depicted in
Figure 2a, their resolution is comparatively poor. All resonance lines are extremely broad, with a full width at half-maximum
kHz, leading to extensive overlap in many spectra. We attribute this line broadening to the strong homo- and heteronuclear dipolar interactions between phosphorus and lithium atoms in the structure. For NH
H
PO
, a
P–
P dipolar coupling constant of 270 Hz was shown to lead to an observed maximum line broadening in the
P single-crystal spectra of
kHz [
13]. The dipolar coupling constants in LDP, calculated from the atomic distances, are 200 Hz (average of the four closest
P), and
Hz (average of the four closest
Li), which means that the ratio of the largest coupling constants and the
’s in NH
H
PO
and LiH
PO
are very similar. Thus, with high certainty, dipolar broadening can be identified as the only factor for the observed line broadening. While additional broadening mechanisms such as orientational disorder or lattice defects cannot be ruled out completely, their extent must be small, in accordance with the findings of a neutron diffraction study [
6].
The variation of the
P chemical shift in LDP we are attempting to extract from resonance lines with
ppm is of the order of
ppm. Consequently, precise localization of the four resonance positions in each spectrum of the rotation pattern is challenging and error-prone. To increase the accuracy for the determined tensors (especially of the quadrupole coupling tensor of
Li, as will be discussed below), we acquired three full rotation patterns over three non-orthogonal (and non-parallel) rotation axes
(
Figure 2b),
(
Figure 3a), and
(
Figure 3b). The three rotation patterns were then subjected to a multi-parameter fit according to Equation (
4), with the motion of the field vector
described by Equation (
5), and the chemical shift tensors given in Equation (
3). To enhance the accuracy of the determined crystal orientation (expressed by the rotation axis orientation and offset angle) for each rotation pattern, we simultaneously fitted the quadrupole coupling tensor of
Li according to Equation (
10) and detailed in
Section 2.2, as the orientation of the LDP single crystal for the measurements of both nuclides is identical. The fit converged on a global solution with the following rotation axes and
P chemical shift tensor components (the error values reflect the fit residuals):
Transformation of the CS tensor from the
frame to the
frame changes
to diagonal form, with the eigenvalues
,
, and
placed on the main diagonal. The weighted trace of
determines the isotropic chemical shift
, with the asymmetry parameter of the CS tensor defined by
. Here, we generally order the tensor components according to the convention
, and make use of the reduced anisotropy
[
14]. The eigenvalues and eigenvectors of the
P CS tensor for LDP are listed in
Table 1 (left). The CS tensor is clearly biaxial, with the asymmetry parameter
reflecting the low site symmetry of Wyckoff site
[
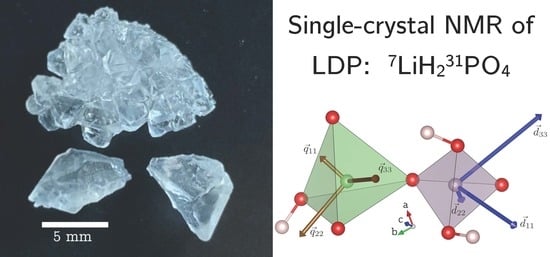
7]. The orientation of the CS tensor eigenvectors in the orthorhombic unit cell of LDP for P(1), scaled according to the associated eigenvalues, are depicted in Figure 7. The eigenvector orientations are free to orient according to the electronic environment generated predominantly by the surrounding oxygen atoms.
As a useful comparison to our single-crystal data, a
P-NMR spectrum of a sample of LDP crushed into a powder was acquired at 5 kHz MAS spinning speed, shown in
Figure 4. The isotropic chemical shift
ppm extracted from this spectrum is in reasonable agreement with the value
ppm derived from single-crystal NMR and identical with the previously reported value from a powder sample under MAS [
5]. To also extract the three eigenvalues of the CS tensor, a Herzfeld–Berger analysis [
15] of the MAS spectrum was performed using the
hba 1.7.5 program [
16]. The results are given in
Table 1 (right), showing that the magnitude of the MAS-derived eigenvalues are in good agreement with the single-crystal values. The error values of the Herzfeld–Berger quantities
, and
are estimated from the contour plots generated by the
hba 1.7.5 program. Due to the steep slope of the contour lines in this plot, the error values of
are estimated to be larger than those of
and are unsymmetric, resulting in different upper and lower error margins for the CS eigenvalues. The narrow signal at 10.5 ppm in
Figure 4 is attributed to the
P chemical shift in aqueous LiH
PO
solution, which is formed over time by the hygroscopic LDP powder with residual moisture in the MAS rotor.
In order to extend the potential of NMR spectroscopy as an analytical tool for inorganic solids, constant efforts are being made trying to relate NMR parameters to structural features of the studied compounds. One example is the correlation of the isotropic chemical shift of
Pb in lead-bearing minerals to the distance of oxygen atoms in the lead coordination sphere [
11]. However, for
P in phosphates, where the first coordination sphere is always formed by covalently bound oxygen atoms, it is notoriously difficult to establish such relations [
17]. One structural parameter that is promising in this context is the dimensionless distortion index (
) of the O–P–O bond angles in the PO
tetrahedra, i.e., their deviation from the ideal tetrahedral angle, 109.47°. According to Baur [
18], the
is defined by:
A distortion of PO
tetrahedra leads to a non-zero value of the
, and is expected to have an effect on the anisotropy of the chemical shift, which in the convention used here [
14], is quantified by the parameter
. For LDP, we find
from the X-ray structure [
6], showing a comparatively strong distortion [
18]. The
P CS anisotropy of
ppm (see
Table 1) is also large, which conforms to expectation. For comparison, the phosphate groups in the mineral pyromorphite, Pb
(PO
)
Cl, exhibit a smaller distortion with
, and accordingly also a smaller CS anisotropy of
ppm [
19]. However, this apparent correlation between the distortion of the tetrahedral geometry and the anisotropy of the
P chemical tensor has only limited validity [
17].
2.2. 7Li NMR of LDP
For
Li with spin
, the quadrupolar coupling between the non-symmetric charge distribution of the nucleus and its electronic surroundings also needs to be considered [
20]. The number of energy levels for a spin
I in an external magnetic field is
, resulting in
NMR transitions, which are classified according to their magnetic quantum number
m. With a particular transition
designated by the parameter
[
21,
22], the resonance frequency
of this transition may then be described by adding the contribution of the quadrupolar interaction to Equation (
1):
Here,
and
are the effects of the quadrupolar interaction described by perturbation theory to first and second order, respectively. For the three transitions of
Li with
, the values for
k are
for the central transition, and
for the two satellite transitions (ST’s). Representative
Li single-crystal NMR spectra of LDP are shown in
Figure 5a, with the satellite pairs for
symmetrically positioned around the non-resolved central transitions of the four independent lithium atoms in the crystal structure. All
Li resonance lines are fairly broad with
kHz, and hence overlap in almost every spectrum. As discussed in detail above for
P, strong homo- and heteronuclear dipolar coupling is assumed to be the dominating effect of line broadening. With similar
Li line widths encountered in other inorganic compounds [
23], no additional broadening mechanism needs to be invoked. The magnitude and orientation dependency of the quadrupolar interaction may be expressed using a quadrupole coupling tensor
. Similar to the electrical field gradient (EFG) tensor
, to which it is related by
, this second-rank tensor is symmetric and traceless, i.e.,
and
. The quadrupolar coupling constant
is equal to the largest
tensor eigenvalue, i.e.,
, and the asymmetry is defined as
, with
. Taking into account the same symmetry arguments as for the CS tensor
of
P at Wyckoff position
given in Equations (
2) and (
3), the
tensors for
Li in the orthorhombic crystal frame of LDP are given by:
These tensors are conveniently determined from the separations (‘splittings’) of the satellite transitions (ST’s) with
for
Li, since these are not affected by either the second-order quadrupolar interaction or the chemical shift. Thus, the difference
of the resonance frequencies depends on the relative orientation of the
tensor to the external magnetic field vector
:
The experimentally determined satellite splittings for
are plotted over the rotation angle
for the three rotation axes
(
Figure 6a),
(
Figure 6b), and
(
Figure 6c) and show a number of comparatively ill-defined data points. However, it has to be kept in mind that for determining the
Li ST splittings in LDP, we need to trace the eight satellite resonances with a
kHz in a limited spectral range of maximum
kHz. Here, the spectral range is defined as the difference between the position of the two outermost satellite transitions. In fact, the average spectral range (calculated over 49
Li spectra and three rotation patterns) is only
kHz and the always overlapping central transitions reduce the localizable range for the ST’s further by their
kHz.
The quadrupole coupling tensors in Equation (
9) were determined by a multi-parameter fit of the experimental splittings according to Equation (
10) with the motion of the field vector
described by Equation (
5), with the fit being coupled to the CS tensor fit of
P to improve accuracy. The rotation axes extracted thereby are given in Equation (
6) and the components of the quadrupole coupling tensor for
Li are (the error values reflect the fit residuals):
kHz,
kHz,
kHz,
kHz, and
kHz. The eigenvalues and the corresponding eigenvectors in the
frame of the
Li
tensor are listed in
Table 2. The quadrupolar coupling constant derived is
kHz and the asymmetry parameter
confirms a biaxial symmetric tensor, as might be expected for Wyckoff position
with the low site symmetry,
. The orientation of the eigenvectors, scaled according to the length of the associated eigenvalue are depicted in
Figure 7.
Having determined the size of the quadrupolar coupling, we can now estimate the extent to which the resonance frequency given in Equation (
8) is affected by the second-order quadrupolar interaction, i.e., the relative magnitude of
. The angle-independent part of the second-order quadrupolar induced shift
provides a quantitative measure for the second-order effect. For the CT (
) of a spin
nuclide at a Larmor frequency of
MHz, this calculates to [
24]:
Obviously, the effects of the quadrupolar interaction to second order for
Li in LDP are negligibly small, especially taking into account the very broad resonance lines. Accordingly, it should now be possible to determine its chemical shift tensor by tracing the variation of the center of the satellite transitions without correcting for second order effects [
21]. However, the chemical shift anisotropy of lithium atoms is generally very small (in the range of 5 ppm [
2]), making detection of anisotropic effects from resonance lines with a
ppm practically impossible. The isotropic chemical shift was, nevertheless, determined from a sample of LDP crushed into a powder and measured at 10 kHz MAS spinning speed. The isotropic shift
ppm extracted thereby is in good agreement with the previously reported value
ppm derived from a polycrystalline powder sample under MAS [
5].