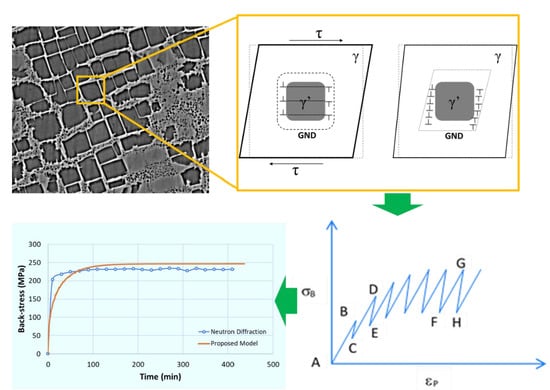
Back-Stress and Its Evolution during Primary Creep in Particle Strengthened Nickel Superalloys
Abstract
:1. Introduction
1.1. Back-Stress
1.2. Back-Stress in Creep
1.3. Neutron Diffraction Studies in Superalloys
2. Back-Stress Model for Particle Reinforced Materials
- (1)
- Stress transfer from γ to γ’ defines primary creep (Postulate-2.1),
- (2)
- completion of the stress transfer process corresponds to the onset of secondary creep (Postulate-2.2), and
- (3)
- saturated value of back-stress is a function only of the applied stress and the volume fraction of the reinforcing particles (Postulate-2.3).
Correlating Neutron Diffraction Results with Back-Stress
3. Experimental Details
Creep Experiment Procedure
4. Results and Discussion
4.1. Effect of Applied Stress on Back-Stress
Effect of a Stress-Jump
4.2. Back-Stress Evolution
4.3. Effect of γ’ Volume Fraction
5. Summary and Conclusions
- The transfer of stress from γ to γ’ has a decelerating effect on creep strain rate, and the attainment of saturation by the phase-specific lattice strains is concomitant with the end of primary creep and the onset of secondary creep.
- The maximum back-stress attained at the end of primary-creep is linearly proportional to the applied stress, with particle volume fraction being the proportionality constant.
- When the applied stress is changed abruptly, the back-stress quickly evolves to reach the maximum level that corresponds to the new applied stress.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eshelby, J.D. Elastic Inclusions and Inhomogeneities. Prog. Solid Mech. 1961, 2, 89–140. [Google Scholar]
- Eshelby, J.D. Distortion of a Crystal by Point Imperfections. J. Appl. Phys. 1954, 25, 255–261. [Google Scholar] [CrossRef]
- Brown, L.M.; Stobbs, W.M. The work hardening of Copper-Silica I: A model based on internal stresses with no plastic relaxation. Philos. Mag. 1971, 23, 1185–1189. [Google Scholar] [CrossRef]
- Ashby, M.F. The deformation of plastically non-homogeneous materials. Philos. Mag. 1970, 170, 399–423. [Google Scholar] [CrossRef]
- Brown, L.M.; Stobbs, W.M. The work hardening of copper-silica V. Equilibrium plastic relaxation by secondary dislocations. Philos. Mag. 1976, 34, 351–372. [Google Scholar] [CrossRef]
- Mori, T.; Mura, T. Calculation of Back-stress decrease caused by climb of Orowan loops in a dispersion hardened alloy. Acta Metall. 1978, 26, 1199–1204. [Google Scholar] [CrossRef]
- Kamat, S.V.; Manoharan, M. Work hardening behavior of alumina particulate reinforced 2024 aluminum alloy matrix composites. J. Compos. Mater. 1993, 27, 1714–1721. [Google Scholar] [CrossRef]
- McLean, M.; Dyson, B.F. Modeling the Effects of Damage and Microstructural Evolution on the Creep Behavior of Engineering Alloys. J. Eng. Mater. Technol. 2000, 22, 273–278. [Google Scholar] [CrossRef]
- Ion, J.C.; Barbosa, A.; Ashby, M.F.; Dyson, B.F.; McLean, M. The Modelling of Creep for Engineering Design-I; NPL Report DMAA115; Middesex: Teddington, UK, 1986. [Google Scholar]
- Dyson, B.F. Microstructure based creep constitutive model for precipitation strengthened alloys—Theory and application. Mater. Sci. Technol. 2009, 25, 213–220. [Google Scholar] [CrossRef]
- Daymond, M.R.; Preuss, M.; Clausen, B. Evidence of variation in slip mode in a polycrystalline nickel-base superalloy with change in temperature from neutron diffraction strain measurements. Acta Mater. 2007, 55, 3089–3102. [Google Scholar] [CrossRef]
- Grant, B.M.B.; Francis, E.M.; Fonseca, J.Q.D.; Daymond, M.R.; Preuss, M. Deformation behaviour of an advanced nickel-based superalloy studied by neutron diffraction and electron microscopy. Acta Mater. 2012, 60, 6829–6841. [Google Scholar] [CrossRef]
- Francis, E.M.; Grant, B.M.B.; Fonseca, J.Q.; Phillips, P.J.; Mills, M.J.; Daymond, M.R.; Preuss, M. High-temperature deformation mechanisms in a polycrystalline nickel-base superalloy studied by neutron diffraction and electron microscopy. Acta Mater. 2014, 74, 18–29. [Google Scholar] [CrossRef]
- Dye, D.; Coakley, J.; Vorontsov, V.; Stone, H.; Rogge, R. Elastic Moduli and load partitioning in a single-crystal nickel superalloy. Scr. Mater. 2009, 61, 109–112. [Google Scholar] [CrossRef]
- Preuss, M.; Fonseca, J.Q.; Grant, B.; Knoche, E.; Moat, R.; Daymond, M. The effect of γ′ particle size on the deformation mechanism in an advanced polycrystalline nickel-base superalloy. Superalloys 2008, 11, 405–414. [Google Scholar]
- Ma, S.; Brown, D.; Bourke, M.; Daymond, M.; Majumdar, B. Microstrain evolution during creep of a high volume fraction superalloy. Mater. Sci. Eng. 2005, 399, 141–153. [Google Scholar] [CrossRef]
- Coakley, J.; Reed, R.; Warwick, J. Lattice strain evolution during creep in single-crystal superalloys. Acta Mater. 2012, 60, 2729–2738. [Google Scholar] [CrossRef]
- Coakley, J.; Ma, D.; Frost, M.; Dye, D.; Seidman, D.; Dunand, D.; Stone, H. Lattice strain evolution and load partitioning during creep of a Ni-based superalloy single crystal with rafted γ′ microstructure. Acta Mater. 2017, 135, 77–87. [Google Scholar] [CrossRef] [Green Version]
- Oruganti, R.; Shukla, A.; Nalawade, S.; Sarkar, S.; Sivakumar, K.G.V.; Vishwanath, T.; Sondhi, S.; Wei, D.; Peck, A.; Bain, K.; et al. A Microstructure-based model for creep of gamma prime strengthened nickel-based Superalloys. J. Eng. Mater. Technol. 2019, 142. [Google Scholar] [CrossRef]









| Material | Ni | Cr | Co | Mo | W | Al | Ti | Nb | Ta |
|---|---|---|---|---|---|---|---|---|---|
| DS-GTD111 † | Bal. | 14.0 | 9.5 | 1.5 | 3.8 | 3.0 | 4.9 | - | 2.8 |
| DS-GTD444 ‡ | Bal. | 9.8 | 7.5 | 1.5 | 6.0 | 4.2 | 3.5 | 0.5 | 4.8 |
| Sample ID | Material | Total γ′ Vol% | γ′ Distribution | Test Condition |
|---|---|---|---|---|
| A2 | DS-GTD111 | 55 | Unimodal | 816 °C, 470 MPa |
| A3 | DS-GTD111 | 55 | Unimodal | 816 °C, 450 MPa |
| A4 | DS-GTD111 | 55 | Unimodal | 816 °C, 414 MPa → 470 MPa |
| M1 | DS-GTD444 | 65 | Bimodal | 871 °C and 414 MPa |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarkar, S.; Gao, Y.; Huang, S.; Bhattacharya, S.; Patil, S.; Oruganti, R. Back-Stress and Its Evolution during Primary Creep in Particle Strengthened Nickel Superalloys. Crystals 2020, 10, 306. https://doi.org/10.3390/cryst10040306
Sarkar S, Gao Y, Huang S, Bhattacharya S, Patil S, Oruganti R. Back-Stress and Its Evolution during Primary Creep in Particle Strengthened Nickel Superalloys. Crystals. 2020; 10(4):306. https://doi.org/10.3390/cryst10040306
Chicago/Turabian StyleSarkar, Sanket, Yan Gao, Shenyan Huang, Saswata Bhattacharya, Swapnil Patil, and Ramkumar Oruganti. 2020. "Back-Stress and Its Evolution during Primary Creep in Particle Strengthened Nickel Superalloys" Crystals 10, no. 4: 306. https://doi.org/10.3390/cryst10040306
APA StyleSarkar, S., Gao, Y., Huang, S., Bhattacharya, S., Patil, S., & Oruganti, R. (2020). Back-Stress and Its Evolution during Primary Creep in Particle Strengthened Nickel Superalloys. Crystals, 10(4), 306. https://doi.org/10.3390/cryst10040306