Structural Dynamics of An ELM-11 Framework Transformation Accompanied with Double-Step CO2 Gate sorption: An NMR Spin Relaxation Study
Abstract
:1. Introduction
2. Experimental
3. Results and Discussion
3.1. CO2 Sorption Isotherms
3.2. Calculating the Second Moment Plateau Values
3.3. Temperature Dependence of T1 in the Closed form of ELM-11
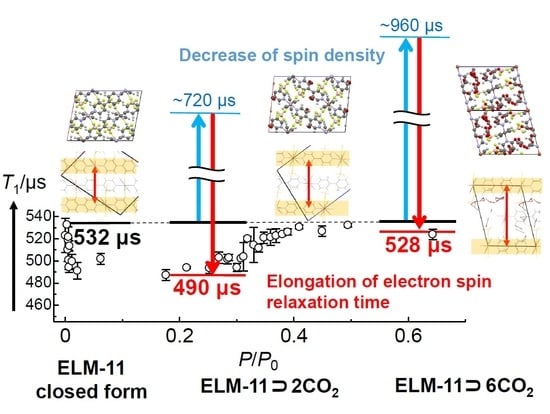
3.4. CO2-Uptake Dependence of T1 in ELM-11
3.5. Spin–Spin Relaxation Time (T2) in ELM-11
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Calculating Second Moments for ELM-11
Appendix A.1. Theoretical Description of the NMR Second Moment

Appendix A.2. 1H Second Moments
| Interaction | Rigid Lattice | Averaged Value | ||
|---|---|---|---|---|
| bpy Flip | BF4− Rotation | bpy Flip + BF4− Rotation | ||
| 1 | ||||
| bpy 1 (0.09°)1 | ||||
| 7.348 | 7.348 | 7.348 | 7.348 | |
| 2.865 | 1.327 | 2.865 | 1.327 | |
| 1.217 | 1.217 | 0.692 | 0.692 | |
| total | 11.43 | 9.892 | 10.905 | 9.367 |
| bpy 2 (54.6°)1 | ||||
| 2.086 | 1.634 | 2.086 | 1.634 | |
| 2.829 | 2.264 | 2.829 | 2.264 | |
| 0.883 | 0.443 | 0.499 | 0.317 | |
| total | 5.798 | 4.341 | 5.414 | 4.215 |
| 2 | ||||
| bpy 1 (0.74°) 1 | ||||
| 5.683 | 5.683 | 5.683 | 5.683 | |
| 1.267 | 1.252 | 1.267 | 1.252 | |
| 1.301 | 1.301 | 0.637 | 0.637 | |
| total | 8.251 | 8.236 | 7.587 | 7.572 |
| bpy 2 (70.64°)1 | ||||
| 1.958 | 1.735 | 1.958 | 1.735 | |
| 1.278 | 1.152 | 1.278 | 1.152 | |
| 0.808 | 0.435 | 0.576 | 0.250 | |
| total | 4.044 | 3.322 | 3.812 | 3.137 |
| 3 | ||||
| bpy 1 (0.52°) 1 | ||||
| 8.454 | 8.454 | 8.454 | 8.454 | |
| 0.664 | 0.572 | 0.664 | 0.572 | |
| 0.712 | 0.712 | 0.370 | 0.370 | |
| total | 9.830 | 9.738 | 9.488 | 9.396 |
| bpy 2 (14.98°) 1 | ||||
| 6.202 | 5.045 | 6.202 | 5.045 | |
| 0.690 | 0.670 | 0.690 | 0.670 | |
| 0.612 | 0.612 | 0.368 | 0.368 | |
| total | 7.504 | 6.327 | 7.260 | 6.083 |
| bpy 1’ (17.52°) 1 | ||||
| 6.093 | 4.756 | 6.093 | 4.756 | |
| 0.725 | 0.540 | 0.725 | 0.540 | |
| 0.682 | 0.682 | 0.373 | 0.373 | |
| total | 7.500 | 5.978 | 7.191 | 5.669 |
| bpy 2’ (49.46°) 1 | ||||
| 2.357 | 1.770 | 2.357 | 1.770 | |
| 0.586 | 0.319 | 0.586 | 0.319 | |
| 0.507 | 0.146 | 0.299 | 0.079 | |
| total | 3.450 | 2.235 | 3.242 | 2.168 |
Appendix A.3. 19F Second Moment Values
| Interaction | Rigid Lattice | Averaged Value | ||
|---|---|---|---|---|
| bpy Flip | BF4− Rotation | bpy Flip + BF4− Rotation | ||
| 1 | ||||
| 6.507 | 6.507 | 0 | 0 | |
| 6.872 | 6.872 | 2.369 | 2.369 | |
| 5.337 | 4.220 | 3.028 | 2.563 | |
| 0.757 | 0.757 | 0 | 0 | |
| 8.660 | 8.660 | 0 | 0 | |
| total | 28.133 | 27.016 | 5.397 | 4.932 |
| 2 | ||||
| 6.337 | 6.337 | 0 | 0 | |
| 6.485 | 6.485 | 0.089 | 0.089 | |
| 5.358 | 5.088 | 3.080 | 2.622 | |
| 0.729 | 0.729 | 0 | 0 | |
| 8.343 | 8.343 | 0 | 0 | |
| total | 27.252 | 26.982 | 3.169 | 2.711 |
| 3 | ||||
| 5.478 | 5.478 | 0 | 0 | |
| 2.811 | 2.811 | 0.040 | 0.040 | |
| 6.302 | 2.486 | 3.537 | 1.308 | |
| 0.628 | 0.628 | 0 | 0 | |
| 7.189 | 7.189 | 0 | 0 | |
| total | 22.408 | 18.592 | 3.577 | 1.348 |
Appendix B. Theoretical Background for NMR Spin-Lattice Relaxation of Multi-Spins

References
- Kitagawa, S.; Kitaura, R.; Noro, S. Functional porous coordination polymers. Angew. Chem. Int. Ed. 2004, 43, 2334–2375. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, A.J.; Thomas, K.M.; Rosseinsky, M.J. Flexibility in metal-organic framework materials: Impact on sorption properties. J. Solid State Chem. 2005, 178, 2491–2510. [Google Scholar] [CrossRef]
- Férey, G. Hybrid porous solids: Past, present, future. Chem. Soc. Rev. 2008, 37, 191–214. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Kaneko, K. Hydrogen bond-regulated microporous nature of copper complex-assembled microcrystals. Chem. Phys. Lett. 2001, 335, 50–56. [Google Scholar] [CrossRef]
- Kitagawa, S.; Matsuda, R. Chemistry of coordination space of porous coordination polymers. Coord. Chem. Rev. 2007, 251, 2490–2509. [Google Scholar] [CrossRef]
- Tanaka, D.; Nakagawa, K.; Higuchi, M.; Horike, S.; Kubota, Y.; Kobayashi, T.C.; Takata, M.; Kitagawa, S. Kinetic gate-opening process in a flexible porous coordination polymer. Angew. Chem. Int. Ed. 2008, 47, 3914–3918. [Google Scholar] [CrossRef] [PubMed]
- Serre, C.; Millange, F.; Thouvenot, C.; Noguès, M.; Marsolier, G.; Louër, D.; Férey, G. Very large breathing effect in the first nanoporous chromium (III)-based solids: MIL-53 or CrIII(OH)·{O2C-C6H4-CO2}·{HO2C-C6H4-CO2H}x·H2Oy. J. Am. Chem. Soc. 2002, 124, 13519–13526. [Google Scholar] [CrossRef] [PubMed]
- Coudert, F.-X.; Jeffroy, M.; Fuchs, A.H.; Boutin, A.; Mellot-Draznieks, C. Thermodynamics of guest-induced structural transitions in hybrid organic-inorganic frameworks. J. Am. Chem. Soc. 2008, 130, 14294–14302. [Google Scholar] [CrossRef] [Green Version]
- Mason, J.A.; Oktawiec, J.; Taylor, M.K.; Hudson, M.R.; Rodriguez, J.; Bachman, J.E.; Gonzalez, M.I.; Cervellino, A.; Guagliardi, A.; Brown, C.M.; et al. Methane storage in flexible metal–organic frameworks with intrinsic thermal management. Nature 2015, 527, 357–361. [Google Scholar] [CrossRef]
- Krause, S.; Bon, V.; Senkovska, I.; Stoeck, U.; Wallacher, D.; Többens, D.M.; Zander, S.; Pillai, R.S.; Maurin, G.; Coudert, F.X.; et al. A pressure-amplifying framework material with negative gas adsorption transitions. Nature 2016, 532, 348–352. [Google Scholar] [CrossRef]
- Tanaka, H.; Hiraide, S.; Kondo, A.; Miyahara, M.T. Modeling and visualization of CO2 adsorption on elastic layer-structured metal−organic framework-11: Toward a better understanding of gate adsorption behavior. J. Phys. Chem. C 2015, 119, 11533–11543. [Google Scholar] [CrossRef]
- Hiraide, S.; Tanaka, H.; Miyahara, M.T. Understanding gate adsorption behaviour of CO2 on elastic layer-structured metal–organic framework-11. Dalton Trans. 2016, 45, 4193–4202. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Yu, Q.; Zhao, Q.; Liang, J.; Dong, J.; Li, J. Adsorption CO2, CH4 and N2 on two different spacing flexible layer MOFs. Micropor. Mesopor. Mater. 2012, 161, 154–159. [Google Scholar] [CrossRef]
- Bon, V.; Senkovska, I.; Wallacher, D.; Heerwig, A.; Klein, N.; Zizak, I.; Feyerherm, R.; Dudzik, E.; Kaskel, S. In situ monitoring of structural changes during the adsorption on flexible porous coordination polymers by X-ray powder diffraction: Instrumentation and experimental results. Micropor. Mesopor. Mater. 2014, 188, 190–195. [Google Scholar] [CrossRef]
- Kondo, A.; Kojima, N.; Kajiro, H.; Noguchi, H.; Hattori, Y.; Okino, F.; Maeda, K.; Ohba, T.; Kaneko, K.; Kanoh, H. Gas adsorption mechanism and kinetics of an elastic layer-structured metal−organic framework. J. Phys. Chem. C 2012, 116, 4157–4162. [Google Scholar] [CrossRef]
- Bousquet, B.; Coudert, F.-X.; Fossati, A.G.J.; Neimark, A.V.; Fuchs, A.H.; Boutin, A. Adsorption induced transitions in soft porous crystals: An osmotic potential approach to multistability and intermediate structures. J. Chem. Phys. 2013, 138, 174706. [Google Scholar] [CrossRef]
- Watanabe, S.; Sugiyama, H.; Adachi, H.; Tanaka, H.; Miyahara, M.T. Free energy analysis for adsorption-induced lattice transition of flexible coordination framework. J. Chem. Phys. 2009, 130, 164707. [Google Scholar] [CrossRef]
- Numaguchi, R.; Tanaka, H.; Watanabe, S.; Miyahara, M.T. Simulation study for adsorption-induced structural transition in stacked-layer porous coordination polymers: Equilibrium and hysteretic adsorption behaviors. J. Chem. Phys. 2013, 138, 054708. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kitaura, R.; Fujimoto, K.; Noro, S.; Kondo, M.; Kitagawa, S. A pillared-layer coordination polymer network displaying hysteretic sorption: [Cu2(pzdc)2(dpyg)]n (pzdc = pyrazine-2,3-dicarboxylate; dpyg = 1,2-di(4-pyridyl)-glycol). Angew. Chem. Int. Ed. 2002, 41, 133–135. [Google Scholar] [CrossRef]
- Kitaura, R.; Seki, K.; Akiyama, G.; Kitagawa, S. Porous coordination-polymer crystals with gated channels specific for supercritical gases. Angew. Chem. Int. Ed. 2003, 42, 428–431. [Google Scholar] [CrossRef]
- Seo, J.; Matsuda, R.; Sakamoto, H.; Bonneau, C.; Kitagawa, S. A Pillared-layer coordination polymer with a rotatable pillar acting as a molecular gate for guest molecules. J. Am. Chem. Soc. 2009, 131, 12792–12800. [Google Scholar] [CrossRef] [PubMed]
- Uemura, K.; Yamasaki, Y.; Komagawa, Y.; Tanaka, K.; Kita, H. Two-step adsorption/desorption on a jungle-gym-type porous coordination polymer. Angew. Chem. Int. Ed. 2007, 46, 6662–6665. [Google Scholar] [CrossRef] [PubMed]
- Hye, J.C.; Dinca, M.; Long, J.R. Broadly hysteretic H2 adsorption in the microporous metal-organic framework Co(1,4-benzenedipyrazolate). J. Am. Chem. Soc. 2008, 130, 7848–7850. [Google Scholar]
- Kondo, A.; Noguchi, H.; Ohnishi, S.; Kajiro, H.; Tohdoh, A.; Hattori, Y.; Xu, W.C.; Tanaka, H.; Kanoh, H.; Kaneko, K. Novel Expansion/shrinkage modulation of 2D layered MOF triggered by clathrate formation with CO2 molecules. Nano Lett. 2006, 6, 2581–2584. [Google Scholar] [CrossRef] [PubMed]
- Kondo, A.; Noguchi, H.; Carlucci, L.; Proserpio, D.M.; Ciani, G.; Kajiro, H.; Ohba, T.; Kanoh, H.; Kaneko, K. Double-step gas sorption of a two−dimensional metal−organic framework. J. Am. Chem. Soc. 2007, 129, 12362–12363. [Google Scholar] [CrossRef] [PubMed]
- Kanoh, H.; Kondo, A.; Noguchi, H.; Kajiro, H.; Tohdoh, A.; Hattori, Y.; Xu, W.C.; Inoue, M.; Sugiura, T.; Morita, K.; et al. Elastic layer-structured metal organic frameworks (ELMs). J. Colloid Interface Sci. 2009, 334, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Kajiro, H.; Noguchi, H.; Kondo, A.; Ohba, T.; Hattori, Y.; Kaneko, K.; Kanoh, H. Tuning of gate opening of an elastic layered structure MOF in CO2 sorption with a trace of alcohol molecules. Langmuir 2011, 27, 6905–6909. [Google Scholar] [CrossRef]
- Ichikawa, M.; Kondo, A.; Noguchi, H.; Kojima, N.; Ohba, T.; Kajiro, H.; Hattori, Y.; Kanoh, H. Double-step gate phenomenon in CO2 sorption of an elastic layer-structured MOF. Langmuir 2016, 32, 9722–9726. [Google Scholar] [CrossRef]
- Hiraide, S.; Tanaka, H.; Ishikawa, N.; Miyahara, M.T. Intrinsic thermal management capabilities of flexible metal−organic frameworks for carbon dioxide separation and capture. ACS Appl. Mater. Interfaces 2017, 9, 41066–41077. [Google Scholar] [CrossRef]
- Kultaeva, A.; Bon, V.; Weiss, M.S.; Pöppl, A.; Kaskel, S. Elucidating the formation and transformation mechanisms of the switchable metal−organic framework ELM-11 by powder and single-crystal EPR study. Inorg. Chem. 2018, 57, 11920–11929. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, J.; Kasumaj, B.; Jeschke, G.; Hunger, M.; Mallat, T.; Baiker, A. Adsorption-desorption induced structural changes of Cu-MOF evidenced by solid state NMR and EPR spectroscopy. J. Am. Chem. Soc. 2009, 131, 2058–2059. [Google Scholar] [CrossRef] [PubMed]
- Panich, A.M.; Sergeev, N.A. Towards determination of distances between nanoparticles and grafted paramagnetic ions by NMR relaxation. Appl. Magn. Reson. 2018, 49, 195–208. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kristinaityte, K.; Zalewski, T.; Kempka, M.; Sakirzanovas, S.; Baziulyte-Paulaviciene, D.; Jurga, S.; Rotomskis, R.; Valeviciene, N.R. Spin–lattice relaxation and diffusion processes in aqueous solutions of gadolinium-based upconverting nanoparticles at different magnetic fields. Appl. Magn. Reson. 2019, 50, 553–561. [Google Scholar] [CrossRef]
- Yamabayashi, T.; Atzori, M.; Tesi, L.; Cosquer, G.; Santanni, F.; Boulon, M.-E.; Morra, E.; Benci, S.; Torre, R.; Chiesa, M.; et al. Scaling up electronic spin qubits into a three-dimensional metal−organic framework. J. Am. Chem. Soc. 2018, 140, 12090–12101. [Google Scholar] [CrossRef]
- Bokor, M.; Marek, T.; Tompa, K. Solid-state NMR of 1-propyltetrazole complexes of iron(II) and zinc(II). 1. 1H spin–lattice relaxation time. J. Magn. Reson. A 1996, 122, 157–164. [Google Scholar] [CrossRef]
- Lim, A.R. Tetragonal-orthorhombic-tetragonal phase transitions in organic-inorganic perovskite-type (CH3NH3)2MnCl4. Solid State Commun. 2017, 267, 18–22. [Google Scholar]
- Jang, S.E.; Kim, M.J.; Lim, A.R. Structural geometry of the layered perovskite-type (CH3CH2CH2NH3)2CuCl4 single crystal near phase transition temperatures. AIP Adv. 2018, 8, 105324. [Google Scholar] [CrossRef] [Green Version]
- Lim, A.R.; Kim, S.H. Study on paramagnetic interactions of (CH3NH3)2CoBr4 hybrid perovskites based on nuclear magnetic resonance (NMR) relaxation time. Molecules 2019, 24, 2895. [Google Scholar] [CrossRef] [Green Version]
- Abragam, A. The Principles of Nuclear Magnetism; Oxford University Press: New York, NY, USA, 1961. [Google Scholar]
- Mikuli, E.; Hetmańczyk, J.; Grad, B.; Kozak, A.; Wąsicki, J.W.; Bilski, P.; Hołderna-Natkaniec, K.; Medycki, W. The relationship between reorientational molecular motions and phase transitions in [Mg(H2O)6](BF4)2, studied with the use of 1H and 19F NMR and FT-MIR. J. Chem. Phys. 2015, 142, 064507. [Google Scholar] [CrossRef]
- Soda, G.; Chihara, H. Note on the theory of nuclear spin relaxation exact formulae in the weak collision limit. J. Phys. Soc. Jpn. 1974, 36, 954–958. [Google Scholar] [CrossRef]
- Wąsicki, J.; Pająk, Z.; Kozak, A. Cation and anion reorientation at phase transition in pyridinium tetrafluoroborate. Z. Naturforsch. 1990, 45a, 33–36. [Google Scholar] [CrossRef]
- Mikuli, E.; Hetmańczyk, Ł.; Medycki, W.; Kowalska, A. Phase transitions and molecular motions in [Zn(NH3)4](BF4)2 studied by nuclear magnetic resonance, infrared and Raman spectroscopy. J. Phys. Chem. Solids 2007, 68, 96–103. [Google Scholar] [CrossRef]
- Mikuli, E.; Grad, B.; Medycki, W.; Hołderna-Natkaniec, K. Phase transitions and molecular motions in [Cd(H2O)6](BF4)2 studied by DSC, 1H and 19F NMR and FT-MIR. J. Solid State Chem. 2004, 177, 3795–3804. [Google Scholar] [CrossRef]
- Pérez-Jiménez, Á.J.; Sancho-García, J.C.; Pérez-Jordá, J.M. Torsional potential of 4,4′-bipyridine: Ab initio analysis of dispersion and vibrational effects. J. Chem. Phys. 2005, 123, 134309. [Google Scholar] [CrossRef] [PubMed]
- Emsley, J.W.; Stephenson, D.S.; Lindon, J.C.; Lunazzi, L.; Pulga, S. Structure and conformation of 4,4′-bipyridyl by nuclear magnetic resonance spectroscopy of a nematic solution. J. Chem. Soc. Perkin Trans. 2 1975, 1541–1544. [Google Scholar] [CrossRef]
- Lowe, I.J.; Tse, D. Nuclear spin-lattice relaxation via paramagnetic centers. Phys. Rev. 1968, 166, 279–291. [Google Scholar] [CrossRef]
- Lee, C.E.; Choi, I.; Kim, J.E.; Lee, C.H. Nuclear magnetic relaxation in dense paramagnet CuF2·2H2O. J. Phys. Soc. Jpn. 1994, 63, 3509–3514. [Google Scholar] [CrossRef]
- Bloembergen, N. On the interaction of nuclear spins in a crystalline lattice. Physica 1949, 15, 386–426. [Google Scholar] [CrossRef]
- Albert, S.; Gutowsky, H.S. Nuclear relaxation and spin exchange in ammonium hexafluorophosphate (NH4PF6). J. Chem. Phys. 1973, 59, 3585–3594. [Google Scholar] [CrossRef]
- Blinc, R.; Lahajnar, G. Magnetic resonance study of molecular motion in cubic (NH4)2SiF6. J. Chem. Phys. 1967, 47, 4146–4152. [Google Scholar] [CrossRef]
- Zdanowska-Frączek, M.; Medycki, W. 1H NMR study of N(CH3)4H(ClF2CCOO)2. Solid State Nucl. Magn. Reson. 2000, 15, 189–193. [Google Scholar] [CrossRef]
- Satterlee, J.D. Fundamental concepts of NMR in paramagnetic systems. Part II: Relaxation effects. Concepts Magn. Reson. 1990, 2, 119–129. [Google Scholar] [CrossRef]
- Moreau, F.; Kolokolov, D.I.; Stepanov, A.G.; Easun, T.L.; Dailly, A.; Lewis, W.; Blake, A.J.; Nowell, H.; Lennox, M.J.; Besley, E.; et al. Tailoring porosity and rotational dynamics in a series of octacarboxylate metal-organic frameworks. Proc. Natl. Acad. Sci. USA 2017, 114, 3056–3061. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Inukai, M.; Fukushima, T.; Hijikata, Y.; Ogiwara, N.; Horike, S.; Kitagawa, S. Control of molecular rotor rotational frequencies in porous coordination polymers using a solid-solution approach. J. Am. Chem. Soc. 2015, 137, 12183–12186. [Google Scholar] [CrossRef]
- Takemura, H.; Nakashima, S.; Kon, N.; Yasutake, M.; Shinmyozu, T.; Inazu, T. A study of C-F···M+ interaction: Metal complexes of fluorine-containing cage compounds. J. Am. Chem. Soc. 2001, 123, 9293–9298. [Google Scholar] [CrossRef] [PubMed]




| Interaction | Motional Mode | ||
|---|---|---|---|
| bpy Flip | BF4− Rotation | bpy Flip + BF4− Rotation | |
| 1 | |||
| bpy 1 | |||
| 0 | 0 | 0 | |
| 1.538 | 0 | 1.538 | |
| 0 | 0.525 | 0.525 | |
| total | 1.538 | 0.525 | 2.063 |
| bpy 2 | |||
| 0.452 | 0 | 0.452 | |
| 0.565 | 0 | 0.565 | |
| 0.44 | 0.384 | 0.566 | |
| total | 1.457 | 0.384 | 1.583 |
| 2 | |||
| bpy 1 | |||
| 0 | 0 | 0 | |
| 0.015 | 0 | 0.015 | |
| 0 | 0.664 | 0.664 | |
| total | 0.015 | 0.664 | 0.679 |
| bpy 2 | |||
| 0.223 | 0 | 0.223 | |
| 0.126 | 0 | 0.126 | |
| 0.373 | 0.232 | 0.558 | |
| total | 0.722 | 0.232 | 0.907 |
| 3 | |||
| bpy 1 | |||
| 0 | 0 | 0 | |
| 0.092 | 0 | 0.092 | |
| 0 | 0.342 | 0.342 | |
| total | 0.092 | 0.342 | 0.434 |
| bpy 2 | |||
| 1.157 | 0 | 1.157 | |
| 0.02 | 0 | 0.02 | |
| 0 | 0.244 | 0.244 | |
| total | 1.177 | 0.244 | 1.421 |
| bpy 1’ | |||
| 1.337 | 0 | 1.337 | |
| 0.185 | 0 | 0.185 | |
| 0 | 0.309 | 0.309 | |
| total | 1.522 | 0.309 | 1.831 |
| bpy 2’ | |||
| 0.587 | 0 | 0.587 | |
| 0.267 | 0 | 0.267 | |
| 0.361 | 0.208 | 0.428 | |
| total | 1.215 | 0.208 | 1.282 |
| bpy 1 | |||
| 0 | 0 | 0 | |
| 0.092 | 0 | 0.092 | |
| 0 | 0.342 | 0.342 | |
| total | 0.092 | 0.342 | 0.434 |
| Interaction | Motional Mode | ||
|---|---|---|---|
| bpy Flip | BF4− Rotation | bpy Flip + BF4− Rotation | |
| 1 | |||
| 0 | 6.507 | 6.507 | |
| 0 | 4.503 | 4.503 | |
| 1.117 | 2.309 | 2.774 | |
| 0 | 0.757 | 0.757 | |
| 0 | 8.66 | 8.660 | |
| total | 1.117 | 22.736 | 23.201 |
| 2 | |||
| 0 | 6.337 | 6.337 | |
| 0 | 6.396 | 6.396 | |
| 0.270 | 2.278 | 2.736 | |
| 0 | 0.729 | 0.729 | |
| 0 | 8.343 | 8.343 | |
| total | 0.270 | 24.083 | 24.541 |
| 3 | |||
| 0 | 5.478 | 5.478 | |
| 0 | 2.771 | 2.771 | |
| 3.816 | 2.765 | 4.994 | |
| 0 | 0.628 | 0.628 | |
| 0 | 7.189 | 7.189 | |
| total | 3.816 | 18.831 | 21.06 |
| Parameter | Expt. | Calc. |
|---|---|---|
| 1H interaction | ||
| τH,0/s | 1.0 × 10−12 | ----- |
| Ea(H)/kJ mol−1 | 18 | ----- |
| ΔM2HH/10−8 T2 | 1.28 | 1.28 |
| ΔM2HF/10−8 T2 | 0.55 | 0.55 |
| 19F interaction | ||
| τF,0/s | 4.0 × 10−14 | ----- |
| Ea(F)/kJ mol−1 | 32 | ----- |
| ΔM2FF/10−8 T2 | 10 | 11.0 |
| ΔM2FH/10−8 T2 | 1.6 | 2.77 |
| ΔM2F11B/10−8 T2 | 7.0 | 8.66 |
| ΔM2F10B/10−8 T2 | 0.61 | 0.76 |
| Parameter | 1 | 2 | 3 | ||
|---|---|---|---|---|---|
| T/K | 273 | 195 | 273 | 195 | 195 |
| T1p, exp/μs | 500 | 532 | 455 | 490 | 529 |
| T1p, calc/μs | 523 | 449 | 490 | 528 | |
| τe/s | 1.22 × 10−11 | 3.08 × 10−11 | 2.59 × 10−11 | 4.05 × 10−11 | |
| D/m2s−1 | 2.87 × 10−16 | 2.87 × 10−16 | 2.87 × 10−16 | ||
| Np/m−3 | 1.91 × 1027 | 1.51 × 1027 | 1.21 × 1027 | ||
| rave.(Cu-Cu)/nm | 0.9105 | 0.9959 | 1.0692 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ohazama, K.; Ueda, T.; Ukai, K.; Ichikawa, M.; Masu, H.; Kajiro, H.; Kanoh, H. Structural Dynamics of An ELM-11 Framework Transformation Accompanied with Double-Step CO2 Gate sorption: An NMR Spin Relaxation Study. Crystals 2020, 10, 328. https://doi.org/10.3390/cryst10040328
Ohazama K, Ueda T, Ukai K, Ichikawa M, Masu H, Kajiro H, Kanoh H. Structural Dynamics of An ELM-11 Framework Transformation Accompanied with Double-Step CO2 Gate sorption: An NMR Spin Relaxation Study. Crystals. 2020; 10(4):328. https://doi.org/10.3390/cryst10040328
Chicago/Turabian StyleOhazama, Kazuki, Takahiro Ueda, Kazuki Ukai, Manami Ichikawa, Hyuma Masu, Hiroshi Kajiro, and Hirofumi Kanoh. 2020. "Structural Dynamics of An ELM-11 Framework Transformation Accompanied with Double-Step CO2 Gate sorption: An NMR Spin Relaxation Study" Crystals 10, no. 4: 328. https://doi.org/10.3390/cryst10040328
APA StyleOhazama, K., Ueda, T., Ukai, K., Ichikawa, M., Masu, H., Kajiro, H., & Kanoh, H. (2020). Structural Dynamics of An ELM-11 Framework Transformation Accompanied with Double-Step CO2 Gate sorption: An NMR Spin Relaxation Study. Crystals, 10(4), 328. https://doi.org/10.3390/cryst10040328