2.1. Operation Principle and Aberration Properties of LC-Based GRIN Lens
Figure 1a,b show the operating principle of the polarization-dependent-switching LC GRIN lens array. The lens array is divided into a polarization-switching layer through which the incident polarization state can be controlled and an LC GRIN lens array that can be optically switched to the periodic focusing or defocusing mode according to the incident polarization state. The LC GRIN lens array has two flat surfaces at the entrance and exit planes of the device structure, where the plano-convex LC layer is formed below the plano-concave isotropic polymer. The refractive index (
np) of the isotropic polymer is identical to the ordinary refractive index (
no) of the LC layer. However, the extraordinary refractive index (
ne) is larger than
np. As shown in
Figure 1a, when the incident polarization state is perpendicular to the alignment axis of the LC layer, the incident light is not refracted according to index-matching conditions (
no =
np), and the structure operates in the defocusing state (2D display mode). By contrast, as shown in
Figure 1b, when the polarization state of the incident light is parallel to the alignment axis of the LC layer, the incident light is periodically refracted owing to the index-mismatching (
ne >
np) condition, and the structure operates in the focusing state (3D display mode). The polarization-switching layer controls the incident polarization state according to the applied voltage. Thus, the stacked module can be switched between the defocusing and focusing modes in a 2D/3D switchable multi-view display.
Figure 1c shows the aberration properties of the polarization-dependent-switching LC GRIN lens array. The spherical aberration of the lens array can be divided into transverse spherical aberration (TSA) and longitudinal spherical aberration (LSA) induced by the difference in the focal length formed by the marginal rays and paraxial rays. Ray distortion caused by the TSA of the LC GRIN lens array can sensitively affect the 3D crosstalk level because of the broad luminance distribution at each viewpoint, resulting from ray distortion in the 3D mode. As shown in
Figure 1c, the polarization-dependent-switching LC GRIN lens array involves additional ray refraction at the flat air-substrate interface, unlike a conventional passive lens array with the plano-convex surface geometry. In particular, the additional refraction further increases the TSA and LSA in a smaller
f-number lens array compared with those of the plano-convex-shaped passive lens. This implies that the aberration values and 3D crosstalk levels of an LC GRIN lens designed for 2D/3D switchable mobile displays would be high. This information should be considered when designing the switchable lens [
30].
In designing the switchable LC GRIN lens array exhibiting an effectively reduced aberration property, the chromatic aberration, induced by the material dispersion, needs to be also considered [
31]. Under the normal dispersion condition of the wavelength-dependent refractive index property of general optical materials, the focal length of a blue-colored light becomes shorter than that of a red-colored light as shown in
Figure 1d. Like the spherical aberration, the chromatic aberration can also be divided into transverse chromatic aberration (TCA) and longitudinal chromatic aberration (LCA). Between both chromatic aberration effects, reducing the TCA effect is more important for achieving an improved 3D crosstalk level, especially in designing a small
f-number lens [
31]. However, unlike the switchable LC lens that forms GRIN profiles within the LC layer operated by fringe fields [
16,
17,
18,
19,
20,
21,
22,
23,
24], the TCA effect of the polarization-dependent-switching LC GRIN lens array on the focusing properties can be effectively reduced by properly choosing the optical materials used for the plano-convex and plano-concave layers. The TCA effect by the material dispersion of the plano-convex LC lens part can be compensated by the TCA effect by the material dispersion of the plano-concave isotropic polymer lens part [
32].
In this study, we designed the interfacial curvature between the plano-convex LC layer and the plano-concave isotropic polymer layer by considering the aberration properties of a small f-number lens. We sectionalized the interfacial curvature into 100 subregions for each elemental lens and used a curvature-fitting procedure to determine the interfacial curvature profile corresponding to the minimum TSA value for the incident rays. We fitted three different curvature functions corresponding to (i) the conventional spherical curvature, (ii) a quadratic polynomial aspherical curvature, and (iii) a high-order (fourth-order) polynomial aspherical curvature. For the different interfacial curvature designs, we analyzed the TSA values for the red, green, and blue wavelengths considering the material dispersion characteristics of real optical materials potentially applicable to the plano-convex birefringent and plano-concave isotropic layers. The TCA properties of the polarization-dependent-switching LC GRIN lens arrays adopting three different interfacial curvatures were also evaluated for comparison.
2.2. Interfacial Curvature Design for LC-Based GRIN Lens with Small F-Number
Figure 2 shows a schematic depicting the interfacial curvature between the plano-concave isotropic polymer layer and the plano-convex-shaped birefringent LC layer of the assembled structure of the LC GRIN lens array. The LC molecules need not be electrically reoriented for switching between the defocusing and focusing modes, which corresponds to switching between the 2D and 3D modes, since the defocusing and focusing modes are determined by the incident polarization state, unlike conventional electrically switching LC lenses. Therefore, the lens can maintain an ideal lens profile according to the designed interfacial curvature shape. In conventional LC lenses, however, the LC is directly electrically reoriented to switch between the focusing and defocusing modes, and the reorientation depends on the applied voltage and complex internal electric field distribution. Therefore, a low-viscosity LC is needed to use a low switching voltage while achieving a relatively fast response time. However, low-viscosity LCs have low-∆
n property, meaning that it is difficult to obtain a small-
f-number lens with a large curvature for the GRIN lens profile determined by the LC geometry. As the structure of polarization-dependent-switching LC GRIN lenses is divided into an LC GRIN lens and the polarization-switching layer, the operating voltage and switching response time are determined by the polarization-dependent-switching layer and not by the LC GRIN lens. Therefore, high-viscosity high-∆
n LCs can be used in the presented polarization-dependent-switching LC GRIN lenses. An advantage of using LCs with high-∆
n in GRIN lenses is that the refractive index difference at the interface between the isotropic polymer layer and the birefringent LC layer is large, and this decreases in the required thickness of the LC layer in the LC GRIN lens, even for a small-
f-number lens. The reduction in the thickness of the lens is very important to obtain an ideal lens profile. In this study, a comparison of two types of polarization-dependent-switching LC GRIN lenses—one with a low-∆
n LC and the other with a high-∆
n LC—was performed by varying the interfacial curvature profile, which was the simulation parameter. For each type of LC, the curvature profiles were designed according to the
xy plane, as shown in
Figure 2.
In this study, the ray-tracing-based Advanced System Analysis Program (ASAP
TM; Breault Research Organization, Inc.) simulation tool was used to analyze the focusing properties of the LC GRIN lenses with the designed curvatures at λ = 550 nm (green).
Figure 3 shows the results of the focusing property simulation for the low-∆n LC GRIN lens for different curvature profiles, namely, spherical, quadratic polynomial aspherical, and high-order polynomial aspherical curvature profiles at the single wavelength (λ = 550 nm). In the LC GRIN lens structure, the refractive index of the isotropic polymer (
np) was
np = 1.51 [
32], and the refractive indices of the LC layer (
ne,
no, ∆
n =
ne –
no) were
ne = 1.69,
no = 1.51, and ∆
n = 0.18, respectively, at λ = 550 nm [
30]. The
f-number and elemental lens pitch of the designed GRIN lens were 1.08 and 285 µm, respectively, irrespective of the type of interfacial curvature. We previously reported a polarization-dependent-switching LC GRIN lens with an
f-number of 4 for 10-view 3D viewing conditions; an elemental lens pitch of 150 μm, viewing window of 15° and a 5.5 inch mobile panel (2560 × 1440, 538 ppi) were used [
30]. In this work, a much smaller
f-number lens (
f-number = 1.08) was considered for a wider 3D viewing window of 50°. In our previous work where the switchable lens was designed for a 3D viewing window of 15°, the use of the quadratic polynomial aspherical interfacial curvature was sufficient to achieve reduced aberration compared with the aberration for the spherical interfacial curvature. Furthermore, for a lens with an
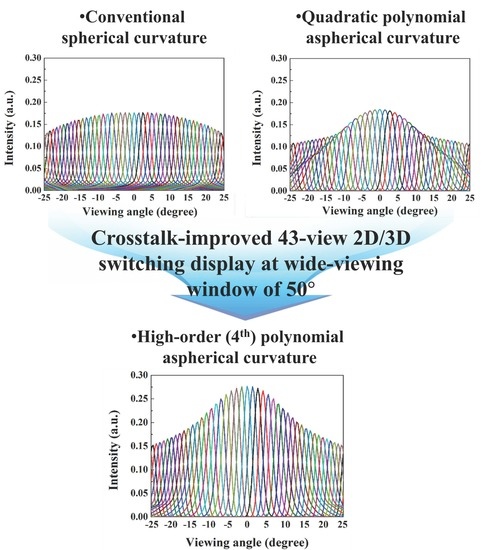
f-number of 1.08, the focusing behavior of the LC GRIN lens with a quadratic polynomial aspherical interfacial curvature was far superior to that with a spherical interfacial curvature, as shown in
Figure 3a,b. However, the aberration properties of
Figure 3b should be improved further for a lens with a considerably small
f-number, which is considered in the present work.
Figure 3c shows that the lens aberration can be considerably improved by adopting a high-order polynomial aspherical curvature for the polarization-dependent-switching LC GRIN lens. The obtained TSA values for the LC GRIN lenses with the three types of interfacial curvatures were 1000.5, 80.1, and 15.2 μm for the spherical, quadratic polynomial, and high-order polynomial aspherical curvatures, respectively. For the different types of interfacial curvatures, the optimized curvature functions for minimizing the TSA and the evaluated TSA values are listed in
Table 1.
Figure 4a,b show the positional curvature profiles and positional curvature slopes of the low-∆
n LC GRIN lens for spherical, quadratic polynomial aspherical, and high-order polynomial aspherical curvatures; the curvature profiles are given by
,
, and
, respectively. The
x and
y values are in millimeters. For the spherical interfacial curvature, the curvature profile function was determined from the elemental lens pitch required for the f-number of the lens. For the quadratic polynomial aspherical and high-order polynomial aspherical curvatures, the curvature functions were derived based on the minimization of the aberration value. According to the curvature profiles in
Figure 4a, the lens thickness of the plano-convex LC layer was 142.5, 175, and 165 μm for the spherical, quadratic polynomial aspherical, and high-order polynomial aspherical curvatures, respectively. As shown in
Figure 1c, the TSA of the lens can be determined from the difference between the focusing of the marginal ray and paraxial ray. To minimize the difference in focal length for these two rays, the curvature slope around the marginal ray must be reduced, while that around the paraxial ray must be increased. When we compare the positional slope of the spherical curvature with those of the aspherical curvatures in
Figure 4b, the curvature slope of the spherical curvature is greater for lens positions around the marginal ray. In addition, the curvature slope for the paraxial ray is the smallest for the spherical curvature. Consequently, the shortest and longest focal lengths are observed for the marginal ray and paraxial ray in the LC GRIN lens with a spherical interfacial curvature, resulting in the lens exhibiting the largest aberration among the three types of lens designs.
In the case of the quadratic polynomial aspherical curvature, the focal length for the marginal ray exceeds that for the paraxial ray, and the focal length difference between them is lower than that for the spherical curvature lens design, as shown in
Figure 3b and
Figure 4b. However, for our small
f-number lens, the relatively large focal length for the marginal rays in the quadratic polynomial aspherical curvature lens prevents further improvement of the aberration properties of the LC GRIN lens although it can be useful for improving the aberration properties of a larger-
f-number lens [
30]. In the case of the high-order polynomial aspherical curvature, the curvature slope around the marginal ray was larger and that around the paraxial ray was lower compared with the curvature slopes for the quadratic polynomial aspherical curvature, as shown in
Figure 3c and
Figure 4b. In the case of the high-order polynomial aspherical curvature, the focal length for the marginal ray is shorter than that for the paraxial ray, similar to the case of the spherical interfacial curvature. However, the focal length difference between the paraxial ray and the marginal ray can be effectively reduced in the case of the high-order polynomial aspherical curvature, even for the small
f-number (=1.08) of the LC GRIN lens.
As explained before, unlike LC-based electro-optic devices that involve direct field-induced switching of the LC layer, a high-∆
n LC can be employed as the plano-convex birefringent layer in a polarization-dependent-switching LC GRIN lens. Ray simulations were performed for the three types of interfacial curvatures by using a high-∆
n LC (∆
n = 0.4 at λ = 550 nm), and the simulation results are shown in
Figure 5. In the high-∆
n LC GRIN lens structure, the refractive index of the isotropic polymer was set to be
np = 1.51, which was identical to the refractive index of the isotropic polymer used in the low-∆
n LC GRIN lens. The refractive indices of the high-∆
n LC were assumed to be
ne = 1.91 and
no = 1.51. The commercially available high-∆
n LC LCM-1107 (LC Matter Co.:
ne = 1.94,
no = 1.54 at λ = 550 nm) has refractive index values similar to those considered in our simulation [
33,
34]. It has been reported that the high-∆
n LCs are not stable under UV exposures in general due to the molecular structures introduced to increase the LC birefringence [
33,
34]. However, unlike the polarization-dependent-switching GRIN lens arrays using the reactive mesogen (RM) as the plano-convex birefringent layer [
30], the polarization-dependent-switching LC GRIN lens arrays do not require the UV exposure process for UV-induced polarization of the RM layer during manufacturing compared with the manufacturing procedures explained in detail in our previous work with the polarization-dependent-switching RM GRIN lens arrays [
30]. The
f-number and lens pitch of the designed high-∆
n LC GRIN lens were 1.08 and 285 µm, respectively, irrespective of the type of interfacial curvature, and these values were identical to those of the low-∆
n LC GRIN lens. For the three types of curvature-fitting functions, the optimized curvature profiles for the minimum TSA were derived, as listed in
Table 1. For the high-∆
n LC, the focusing properties of the three curvatures shown in
Figure 5a–c are superior to those for the low-∆
n LC shown in
Figure 3a–c. The determined TSA values of the LC GRIN lenses with spherical, quadratic polynomial, and high-order polynomial aspherical curvatures were 100.3, 30.4, and 10.2 μm, respectively, which are lower than the TSA values of the low-∆
n LC GRIN lens for these curvatures by factors of 10, 2.6, and 1.5, respectively. Similar to the case of the low-∆
n LC GRIN lenses, the smallest and largest TSA values of the high-∆
n LC GRIN lenses were observed for the high-order polynomial aspherical curvature and spherical curvature, respectively, and the reason for this observation is identical to that presented for
Figure 3 and
Figure 4.
Figure 6a,b show positional curvature profiles and positional curvature slopes for the high-∆
n LC GRIN lenses with spherical, quadratic polynomial aspherical, and high-order polynomial aspherical curvatures. The curvature profiles of the designed lenses were
(spherical curvature),
(quadratic polynomial aspherical curvature), and
(high-order polynomial aspherical curvature). As shown in
Figure 6a, the thickness required for the plano-convex LC layer was 85, 75, and 72 μm for the spherical, quadratic polynomial aspherical, and high-order polynomial aspherical profiles, respectively. For all the curvatures, the LC layer thickness required for the high-∆
n LC GRIN lens was smaller than that required for the low-∆
n LC GRIN lens, which is evident from
Table 1. From the practical viewpoint of the manufacturing yield, a considerably small LC layer thickness can facilitate the uniformity of the homogeneously planar LC alignment, although the ideal LC alignment was assumed in our simulation analysis. Importantly, the use of the high-∆
n LC for the LC GRIN lens led to the positional curvature slopes for both the marginal ray and paraxial ray being considerably smaller than those for the low-∆
n LC GRIN lens with the same
f-number (
Figure 4b and
Figure 6b). Furthermore, the TSA values of the designed curvatures of the high-∆
n LC GRIN lens can be further reduced, unlike the case of the low-∆
n LC GRIN lens. These results show that an LC material with high-∆
n as well as an optimized aspherical curvature design can minimize the TSA of the 2D/3D switchable LC GRIN lens with a small
f-number. For the three interfacial curvatures designed for the high-∆
n LC GRIN lens arrays, the practically available optical material conditions were applied to the polarization-dependent-switching LC GRIN lens array structures to analyze the aberration effects by the material dispersion characteristics and their wavelength-dependent TSA and TCA properties were evaluated. As the plano-convex high-∆
n LC and plano-concave isotropic layers, the material dispersion curves of LCM 1107 and UV-cured NOA81, respectively, were used [
32,
33,
34]. The Cauchy equations used to consider the material dispersion properties in our aberration analysis are
In Equations (1) and (2),
ne(λ) and
no(λ) are the Cauchy functions of the high-∆
n LC of LCM 1107. Equation (3) for
np(λ) is the Cauchy function of NOA81. As shown in
Figure 7a, the two Cauchy curves of
ne(λ) and
np(λ) have similar dispersion characteristics and
ne = 1.916 and
np = 1.492 for λ = 630 nm (red),
ne = 1.940 and
np = 1.511 for λ = 550 nm (green), and
ne = 2.004 and
np = 1.565 for λ = 450 nm (blue). Thus, although the (
ne-
np) amount becomes slightly increased with decreasing wavelength, the wavelength-dependence of the (
ne−
np) values is negligible, as shown in
Figure 7b, exhibiting a small value of maximum deviation of 0.009 at λ = 450 nm from the average amount of <
ne−
np> = 0.430 over the entire visible region. Compared with the dispersion property of the (
ne−
np) value for the 3D mode operation, the dispersion property of the (
no−
np) value for the 2D mode operation shows a relatively higher wavelength dependency, as shown in
Figure 7a,b. However, the average of the (
no−
np) values over the visible region is 0.0256, exhibiting quite a low level of index mismatching. For achieving a more ideal index-matching condition over the entire visible region, a further material optimization would be needed.
When the material dispersion conditions shown in
Figure 7 were applied to the high-∆
n LC GRIN lens arrays designed with the three different interfacial curvatures listed in
Table 1, the wavelength-dependent TSA values listed in
Table 2 show the minimum at λ = 630 nm (red) and the maximum at λ = 450 nm (blue) identically for three types of interfacial curvatures because the interfacial curvatures shown in
Table 1 were designed with the assumption that the refractive index condition of
ne−
np = 0.4, which matches better in the red light rather than the blue light in the case of using the commercially available materials of LCM 1107 and NOA81. However, the wavelength-dependent TSA values of
Table 2 do not show a meaningful difference between each other over the entire visible range for each interfacial curvature design condition, although the refractive indices of LCM 1107 and NOA81 are highly dependent on the wavelength, as shown in the dispersion curves of
Figure 7a. Among the three interfacial curvature designs, the TSA values were the lowest over the whole visible range in the case of using the high-order polynomial aspherical curvature. The variation of the wavelength-dependent TSA values was also the lowest under the high-order polynomial aspherical curvature condition.
Using the material dispersion values, the TCA properties according to the interfacial curvature designs were also characterized, as shown in
Figure 8. For the spherical, quadratic polynomial, and high-order polynomial aspherical interfacial curvatures, the TCA values over the visible range were derived as TCA = 13.4 μm, 12.2 μm, and 11.5 μm, respectively, as listed in
Table 2. For all cases, the TCA values were lower than the TSA values, indicating that it is more important to reduce the TSA properties by employing the well-designed interfacial curvature in a small
f-number lens. It is worthwhile to note that the TSA value of the LC GRIN lens array with the spherical interfacial curvature is quite large but the TCA value is quite small. In the polarization-dependent- switching LC GRIN lens array, the wavelength-dependent TSA and TCA properties are determined by the dispersion characteristics of (
ne−
np) not by the individual dispersion properties of
ne(λ) and
np(λ). One of the merits of the presented switchable lens type is that the wavelength-dependent aberration effect in the plano-convex lens can be effectively compensated with that in the plano-concave lens by properly choosing the optical materials of the plano-convex and plano-concave lens parts for the (
ne−
np) value to be nearly constant over the visible range. For comparison, the wavelength-dependent ray simulation result for the single-layered plano-convex lens with the spherical curvature at the polymer-air interface is presented in
Figure 8a, where the NOA81 was used as the isotropic polymer layer. In
Figure 8a, the lens conditions of the lens pitch, the focal length, and the
f-number were the same as those of
Figure 8b–d. However, the TCA value in
Figure 8a was 59.4 μm, which was much higher than the TCA values obtained in three types of the polarization-dependent-switching LC GRIN lens arrays. These results clearly indicate that the presented lens type of the polarization-dependent-switching LC GRIN lens array utilizing the index mismatching condition between two assembled optical layers of the plano-convex and plano-concave lenses is advantageous compared to the single-layered switchable lens types, such as the field-driven LC-switching GRIN lenses [
16,
17,
18,
19,
20,
21,
22,
23,
24], in reducing the TCA properties, especially for a small
f-number lens design with a highly-dispersive high-Δ
n LC.