Spontaneous Growth of CaBi4Ti4O15 Piezoelectric Crystal Using Mixed Flux Agents
Abstract
:1. Introduction
2. Materials and Methods
2.1. Polycrystalline Preparation
2.2. Flux Selection and Growth of CBT Crystal
2.3. Transmission Spectra Measurement and Phase Characterization
2.4. Theoretical Calculations
3. Results and Discussion
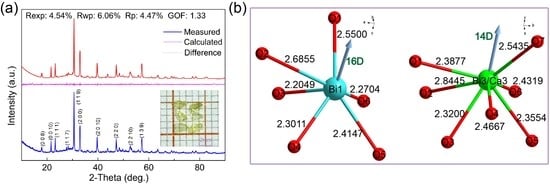
3.1. XRPD Analysis and Crystallization
3.2. Structure–Morphology Relationships
3.3. Piezoelectric Activity Evaluation
3.3.1. Transmission Spectra
3.3.2. Dipole Moment Calculation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, S.J.; Yu, F.P. Piezoelectric materials for high temperature sensors. J. Am. Ceram. Soc. 2011, 94, 3153–3170. [Google Scholar] [CrossRef]
- Jiang, X.N.; Kim, K.; Zhang, S.J.; Johnson, J.; Salazar, G. High-temperature piezoelectric sensing. Sensors 2014, 14, 144–169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, J.G.; Gao, X.Y.; Chen, J.G.; Wang, C.M.; Zhang, S.J.; Dong, S.X. Review of high temperature piezoelectric materials, devices, and applications. Acta Phys. Sin. 2018, 67, 207701. [Google Scholar]
- Yokota, Y.; Ohashi, Y.; Kudo, T.; Kochurikhin, V.V.; Medvedev, A.; Kurosawa, S.; Kamada, K.; Yoshikawa, A. Effects of Al Substitution for Ca3Ta(Ga1−xAlx)3Si2O14 Piezoelectric Single Crystals. J. Cryst. Growth 2017, 468, 321–325. [Google Scholar] [CrossRef]
- Hagiwara, M.; Noguchi, H.; Hoshina, T.; Takeda, H.; Fujihara, S.; Kodama, N.; Tsurumi, T. Growth and Characterization of Ca2Al2SiO7 Piezoelectric Single Crystals for High-Temperature Sensor Applications. Jpn. J. Appl. Phys. 2013, 52, 09KD03. [Google Scholar] [CrossRef]
- Zhang, S.J.; Fei, Y.T.; Frantz, E.; Snyder, D.W.; Chai, B.H.T.; Shrout, T.R. High-Temperature Piezoelectric Single Crystal ReCa4O(BO3)3 for Sensor Applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 2703–2708. [Google Scholar] [CrossRef]
- Zheng, L.Y.; Li, G.R.; Zhang, W.Z.; Yin, Q.R. The Structure and Properties of Bi-Layered Piezoelectric Ceramics Bi4(Ca, Sr)Ti4O15. Jpn. J. Appl. Phys. 2002, 41, L1471–L1473. [Google Scholar] [CrossRef]
- Yan, H.X.; Li, C.E.; Zhou, J.G.; Zhu, W.M.; He, L.X.; Song, Y.X.; Yu, Y.H. Effects of A-Site (NaCe) Substitution with Na-Deficiency on Structures and Properties of CaBi4Ti4O15-Based High-Curie-Temperature Ceramics. Jpn. J. Appl. Phys. 2001, 40, 6501–6505. [Google Scholar] [CrossRef]
- Subbarao, E.C. A Family of Ferroelectric Bismuth Compounds. J. Phys. Chem. Solids 1962, 23, 665–676. [Google Scholar] [CrossRef]
- Khokhar, A.; Mahesh, M.L.V.; James, A.R.; Goyal, P.K.; Sreenivas, K. Sintering Characteristics and Electrical Properties of BaBi4Ti4O15 Ferroelectric Ceramics. J. Alloy. Compd. 2013, 581, 150–159. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Li, Y.C.; Hui, S.P.; Dong, X.L. Effect of Tungsten Doping in Bismuth-Layered Na0.5Bi2.5Nb2O9 High Temperature Piezoceramics. Appl. Phys. Lett. 2014, 104, 012904. [Google Scholar] [CrossRef]
- Takeuchi, T.; Tani, T.; Saito, Y. Piezoelectric Properties of Bismuth Layer-Structured Ferroelectric Ceramics with a Preferred Orientation Processed by the Reactive Templated Grain Growth Method. Jpn. J. Appl. Phys. 1999, 38, 5553–5556. [Google Scholar] [CrossRef]
- Jaeger, R.E.; Egerton, L. Hot Pressing of Potassium-Sodium Niobates. J. Am. Ceram. Soc. 1962, 45, 209–213. [Google Scholar] [CrossRef]
- Lin, D.B.; Li, Z.R.; Zhang, S.J.; Xu, Z.; Yao, X. Dielectric/Piezoelectric Properties and Temperature Dependence of Domain Structure Evolution in Lead Free (K0.5Na0.5)NbO3 single crystal. Solid State Commun. 2009, 149, 1646–1649. [Google Scholar] [CrossRef]
- Tang, D.Y.; Xia, Y.N.; Wu, B.C.; Chen, C.T. Growth of A New UV Nonlinear Optical Crystal: KBe2(BO3)F2. J. Cryst. Growth 2001, 222, 125–129. [Google Scholar] [CrossRef]
- Tellier, T.; Boullay, P.; Manier, M.; Mercurio, D. A Comparative Study of the Aurivillius Phase Ferroelectrics CaBi4Ti4O15 and BaBi4Ti4O15. J. Solid State Chem. 2004, 177, 1829–1837. [Google Scholar] [CrossRef]
- Dong, M.; Ye, Z.G. High-Temperature Solution Growth and Characterization of the Piezo-/Ferroelectric (1−x)Pb(Mg1/3Nb2/3)O3-xPbTiO3 [PMNT] single crystals. J. Cryst. Growth 2000, 209, 81–90. [Google Scholar] [CrossRef]
- Saitoh, S.; Takeuchi, T.; Kobayashi, T.; Harada, K.; Shimanuki, S.; Yamashita, Y. An Improved Phased Array Ultrasonic Probe Using 0.91Pb(Zn1/3Nb2/3)O3-0.09PbTiO3 Single Crystal. Jpn. J. Appl. Phys. 1999, 38, 3380–3384. [Google Scholar] [CrossRef]
- Yamashita, Y.; Shimanuki, S. Synthesis of Lead Scandium Niobate-Lead Titanate Pseudo Binary System Single Crystals. Mater. Res. Bull. 1996, 31, 887–895. [Google Scholar] [CrossRef]
- Brunskill, I.H.; Boutellier, R.; Depmeier, W.; Schmid, H. High-Temperature Solution Growth of Pb(Fe0.5Nb0.5)O3 and Pb(Mn0.5Nb0.5)O3 Crystals. J. Cryst. Growth 1982, 56, 541–546. [Google Scholar] [CrossRef]
- Brixel, W.; Boutellier, R.; Schmid, H. Flux Growth and Characterization of Single Crystals of the Perovskites Pb2FeTaO6 and Pb2CoWO6. J. Cryst. Growth 1987, 82, 396–404. [Google Scholar] [CrossRef] [Green Version]
- Ye, Z.G.; Tissot, P.; Schmid, H. Pseudo-Binary Pb(Mg1/3Nb2/3)O3-PbO Phase Diagram and Crystal Growth of Pb(Mg1/3Nb2/3)O3 [PMN]. Mater. Res. Bull. 1990, 25, 739–748. [Google Scholar] [CrossRef]
- Sun, B.N.; Boutellier, R.; Sciau, P.; Burkhardt, E.; Rodriguez, V.; Schmid, H. High Temperature Solution Growth of Perovskite Pb2CoWO6 Single Crystals. J. Cryst. Growth 1991, 112, 71–83. [Google Scholar] [CrossRef]
- Ye, Z.G.; Schmid, H. Growth From High Temperature Solution and Characterization of Pb(Fe2/3W1/3)O3 Single Crystals. J. Cryst. Growth 1996, 167, 628–637. [Google Scholar] [CrossRef]
- Elwell, D.; Sheel, H.J. Crystal Growth from High Temperature Solution, 3rd ed.; Academic Press: New York, NY, USA, 1975; pp. 94–95. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for ab initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid Functionals Based on a Screened Coulomb Potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef] [Green Version]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Kennedy, B.J.; Zhou, Q.D.; Ismunandar; Kubota, Y.; Kato, K. Cation Disorder and Phase Transitions in the Four-Layer Ferroelectric Aurivillius Phases ABi4Ti4O15 (A = Ca, Sr, Ba, Pb). J. Solid State Chem. 2008, 181, 1377–1386. [Google Scholar] [CrossRef]
- Tanwar, A.; Sreenivas, K.; Gupta, V. Effect of Orthorhombic Distortion on Dielectric and Piezoelectric Properties of CaBi4Ti4O15 Ceramics. J. Appl. Phys. 2009, 105, 084105. [Google Scholar] [CrossRef]
- Halasyamani, P.S. Asymmetric Cation Coordination in Oxide Materials: Influence of Lone-Pair Cations on the Intra-Octahedral Distortion in d0 Transition Metals. Chem. Mater. 2004, 16, 3586–3592. [Google Scholar] [CrossRef]
- Brese, N.E.; O’Keeffe, M. Bond-Valence Parameters for Solids. Acta Cryst. B 1991, 47, 192–197. [Google Scholar] [CrossRef]
- Ok, K.M.; Halasyamani, P.S. Mixed-Metal Tellurites: Synthesis, Structure, and Characterization of Na1.4Nb3Te4.9O18 and NaNb3Te4O16. Inorg. Chem. 2005, 44, 3919–3925. [Google Scholar] [CrossRef]
- Maggard, P.A.; Nault, T.S.; Stern, C.L.; Poeppelmeier, K.R. Alignment of Acentric MoO3F33− Anions in a Polar Material: (Ag3MoO3F3)(Ag3MoO4)Cl. J. Solid State Chem. 2003, 175, 27–33. [Google Scholar] [CrossRef]
- Izumi, H.K.; Kirsch, J.E.; Stern, C.L.; Poeppelmeier, K.R. Examining the Out-of-Center Distortion in the [NbOF5]2− Anion. Inorg. Chem. 2005, 44, 884–895. [Google Scholar] [CrossRef]
- Kim, J.H.; Halasyamani, P.S. A Rare Multi-Coordinate Tellurite, NH4ATe4O9·2H2O (A = Rb or Cs): The Occurrence of TeO3, TeO4, and TeO5 Polyhedra in the Same Material. J. Solid State Chem. 2008, 181, 2108–2112. [Google Scholar] [CrossRef]
- Chen, F.F.; Jiang, C.; Tian, S.W.; Yu, F.P.; Cheng, X.F.; Duan, X.L.; Wang, Z.P.; Zhao, X. Electroelastic Features of Piezoelectric Bi2ZnB2O7 Crystal. Cryst. Growth Des. 2018, 18, 3988–3996. [Google Scholar] [CrossRef]






| Crystal | Species | ∆d (Å) | Dipole Moments | ||||
|---|---|---|---|---|---|---|---|
| x (a) | y (b) | z (c) | Debye | ×10−4 edu·cm/Å3 | |||
| CBT * | Bi(1)O6 | 1.37 | −2.0168 | −6.7630 | −14.5406 | 16.16 | 541.46 |
| Ca(1)/Bi(2)O8 | 0.60 | −9.9685 | −0.1447 | 0 | 9.97 | 333.99 | |
| Ca(3)/Bi(3)O7 | - | −8.2239 | 3.3904 | 10.8491 | 14.03 | 470.00 | |
| Ti(1)O6 | 0.44 | 4.3457 | 0.0852 | −2.8455 | 5.20 | 174.04 | |
| Ti(2)O6 | 0.69 | 2.3948 | −0.5329 | −8.4905 | 8.84 | 296.07 | |
| Unit cell | - | 0 | 0 | −37.35 | −37.35 | −312.78 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, M.; Wu, G.; Yu, F.; Li, L.; Li, Y.; Cheng, X.; Zhao, X. Spontaneous Growth of CaBi4Ti4O15 Piezoelectric Crystal Using Mixed Flux Agents. Crystals 2020, 10, 698. https://doi.org/10.3390/cryst10080698
Fan M, Wu G, Yu F, Li L, Li Y, Cheng X, Zhao X. Spontaneous Growth of CaBi4Ti4O15 Piezoelectric Crystal Using Mixed Flux Agents. Crystals. 2020; 10(8):698. https://doi.org/10.3390/cryst10080698
Chicago/Turabian StyleFan, Mengdi, Guangda Wu, Fapeng Yu, Lili Li, Yanlu Li, Xiufeng Cheng, and Xian Zhao. 2020. "Spontaneous Growth of CaBi4Ti4O15 Piezoelectric Crystal Using Mixed Flux Agents" Crystals 10, no. 8: 698. https://doi.org/10.3390/cryst10080698
APA StyleFan, M., Wu, G., Yu, F., Li, L., Li, Y., Cheng, X., & Zhao, X. (2020). Spontaneous Growth of CaBi4Ti4O15 Piezoelectric Crystal Using Mixed Flux Agents. Crystals, 10(8), 698. https://doi.org/10.3390/cryst10080698