Surface Stabilized Topological Solitons in Nematic Liquid Crystals
Abstract
:1. Introduction
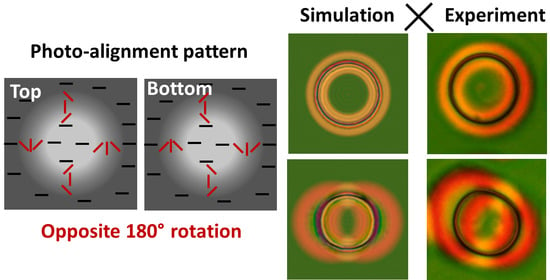
2. Materials and Methods
φ = +/− π (r − rin)/(rout − rin) for rin < r < rout,
φ = +/− π for r > rout
ne = 1.67906 + 0.01546 µm2/λ2 + 0.001663 µm4/λ4
3. Results
3.1. Experimental Results
3.2. Simulation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Peng, C.; Turiv, T.; Guo, Y.; Shiyanovskii, S.V.; Wei, Q.-H.; Lavrentovich, O.D. Control of colloidal placement by modulated molecular orientation in nematic cells. Sci. Adv. 2016, 2, e1600932. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Babakhanova, B.; Yu, H.; Chaganava, I.; Wei, Q.-H.; Shiller, P.; Lavrentovich, O.D. Controlled Placement of Microparticles at the Water—Liquid Crystal Elastomer Interface. ACS Appl. Mater. Interface 2019, 11, 15007–15013. [Google Scholar] [CrossRef] [PubMed]
- Babakhanova, B.; Turiv, T.; Guo, Y.; Hendrikx, M.; Wei, Q.-H.; Schenning, A.P.H.J.; Broer, D.J.; Lavrentovich, O.D. Liquid crystal elastomer coatings with programmed response of surface profile. Nat. Commun. 2018, 9, 456. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zeng, H.; Wani, O.M.; Wasylczyk, P.; Kaczmarek, R.; Priimagi, A. Self-Regulating Iris Based on Light-Actuated Liquid Crystal Elastomer. Adv. Mater. 2017, 29, 1–7. [Google Scholar] [CrossRef]
- Peng, C.; Turiv, T.; Guo, Y.; Wei, Q.-H.; Lavrentovich, O.D. Command of active matter by topological defects and patterns. Science 2016, 354, 882–885. [Google Scholar] [CrossRef] [Green Version]
- Kobashi, J.; Yoshida, H.; Ozaki, M. Planar optics with patterned chiral liquid crystals. Nat. Photonics 2016, 10, 389–392. [Google Scholar] [CrossRef]
- Nys, I.; Stebryte, M.; Ussembayev, Y.Y.; Beeckman, J.; Neyts, K. Tilted chiral liquid crystal gratings for efficient large-angle diffraction. Adv. Opt. Mater. 2019, 7, 1901364. [Google Scholar] [CrossRef]
- Xiang, X.; Kim, J.; Escuti, M.J. Bragg polarization gratings for wide angular bandwidth and high efficiency at steep deflection angles. Sci. Rep. 2018, 8, 10–15. [Google Scholar] [CrossRef] [Green Version]
- Jiang, M.; Yu, H.; Feng, X.; Guo, Y.; Chaganava, I.; Turiv, T.; Lavrentovich, O.D.; Wei, Q.-H. Liquid Crystal Pancharatnam—Berry Micro-Optical Elements for Laser Beam Shaping. Adv. Opt. Mater. 2018, 6, 1800961. [Google Scholar] [CrossRef]
- Yaroshchuk, O.; Reznikov, Y. Photoalignment of liquid crystals: Basics and current trends. J. Mater. Chem. 2012, 22, 286. [Google Scholar] [CrossRef]
- Chigrinov, V. Photoaligning and Photopatterning—A New Challenge in Liquid Crystal Photonics. Crystals 2013, 3, 149–162. [Google Scholar] [CrossRef] [Green Version]
- Bisoyi, H.K.; Li, Q. Light-Driven Liquid Crystalline Materials: From Photo-Induced Phase Transitions and Property Modulations to Applications. Chem. Rev. 2016, 116, 15089–15166. [Google Scholar] [CrossRef] [PubMed]
- Miskiewicz, M.N.; Escuti, M.J. Direct-writing of complex liquid crystal patterns. Optics Express 2014, 22, 12691. [Google Scholar] [CrossRef] [PubMed]
- De Sio, L.; Roberts, D.E.; Liao, Z.; Nersisyan, S.; Uskova, O.; Wickboldt, L.; Tabiryan, N.; Steeves, D.M.; Kimball, B.R. Digital polarization holography advancing geometrical phase optics. Optics Express 2016, 24, 18297–18306. [Google Scholar] [CrossRef]
- Berteloot, B.; Nys, I.; Poy, G.; Beeckman, J.; Neyts, K. Ring-shaped liquid crystal structures through patterned planar photo-alignment. Soft Matter 2020, 16, 4999–5008. [Google Scholar] [CrossRef]
- Guo, Y.; Jian, M.; Peng, C.; Sun, K.; Yaroshchuk, O.; Lavrentovich, O.; Wei, Q.-H. High-Resolution and High-Throughput Plasmonic Photopatterning of Complex Molecular Orientations in Liquid Crystals. Adv. Mater. 2016, 28, 2353–2358. [Google Scholar] [CrossRef]
- Marrucci, L.; Manzo, C.; Paparo, D. Pancharatnam-Berry phase optical elements for wave front shaping in the visible domain: Switchable helical mode generation. Appl. Phys. Lett. 2006, 88, 221102. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, U.; Pagliusi, P.; Provenzano, C.; Lepera, E.; Cipparrone, G. Liquid crystal microlens arrays recorded by polarization holography. Appl. Optics 2015, 54, 3303–3307. [Google Scholar] [CrossRef]
- Chen, P.; Lu, Y.Q.; Hu, W. Beam shaping via photopatterned liquid crystals. Liq. Cryst. 2016, 43, 2051–2061. [Google Scholar] [CrossRef]
- Larocque, H.; Gagnon-Bischoff, J.; Bouchard, F.; Fickler, R.; Upham, J.; Boyd, R.W.; Karimi, E. Arbitrary optical wavefront shaping via spin- to-orbit coupling. J. Optics 2016, 18, 124002. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Li, Y.; Yokoyama, H. Artificial web of disclination lines in nematic liquid crystals. Nat. Commun. 2017, 8, 389–392. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Provenzano, C.; Pagliusi, P.; Cipparrone, G. Electrically tunable two-dimensional liquid crystals gratings induced by polarization holography. Optics Express 2007, 15, 5872–5878. [Google Scholar] [CrossRef] [PubMed]
- Nys, I.; Beeckman, J.; Neyts, K. Switchable 3D liquid crystal grating generated by periodic photo-alignment on both substrates. Soft Matter 2015, 11, 7802–7808. [Google Scholar] [CrossRef] [PubMed]
- Nys, I.; Nersesyan, V.; Beeckman, J.; Neyts, K. Complex liquid crystal superstructures induced by periodic photo-alignment at top and bottom substrate. Soft Matter 2015, 14, 6892–6902. [Google Scholar] [CrossRef] [PubMed]
- Nersesyan, V.; Nys, I.; Van Acker, F.; Wang, C.-T.; Beeckman, J.; Neyts, K. Observation of symmetry breaking in photoalignment-induced periodic 3D LC structures. J. Mol. Liq. 2020, 306, 112864. [Google Scholar] [CrossRef]
- Ouchi, T.; Imamura, K.; Sunami, K.; Yoshida, H.; Ozaki, M. Topologically Protected Generation of Stable Wall Loops in Nematic Liquid Crystals. Phys. Rev. Lett. 2019, 123, 097801. [Google Scholar] [CrossRef]
- Sunami, K.; Imamura, K.; Ouchi, T.; Yoshida, H.; Ozaki, M. Shape control of surface-stabilized disclination loops in nematic liquid crystals. Phys. Rev. E 2018, 97, 020701. [Google Scholar] [CrossRef] [Green Version]
- Honma, M.; Toyoshima, W.; Nose, T. Bistable liquid crystal device fabricated via microscale liquid crystal alignment. J. Appl. Phys. 2016, 120, 143105. [Google Scholar] [CrossRef]
- Honma, M.; Takahashi, K.; Yamaguhi, R.; Nose, T. Driving voltage properties sensitive to microscale liquid crystal orientation pattern in twisted nematic liquid crystal cells. Jpn. J. Appl. Phys. 2016, 55, 041701. [Google Scholar] [CrossRef]
- Honma, M.; Nose, T. Twisted nematic liquid crystal polarization grating with the handedness conservation of a circularly polarized state. Optics Express 2012, 20, 18449–18458. [Google Scholar] [CrossRef]
- Ackerman, P.J.; van de Lagemaat, J.; Smalyukh, I.I. Self-assembly and electrostriction of arrays and chains of hopfion particles in chiral liquid crystals. Nat. Commun. 2015, 6, 6012. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smalyukh, I.I.; Lansac, Y.; Clark, N.A.; Trivedi, R.P. Three-dimensional structure and multistable optical switching of triple-twisted particle-like excitations in anisotropic fluids. Nat. Mater. 2010, 9, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Varanytsia, A.; Chien, L.-C. Photoswitchable and dye-doped bubble domain texture of cholesteric liquid crystals. Optics Lett. 2015, 40, 4392. [Google Scholar] [CrossRef] [PubMed]
- Loussert, C.; Brasselet, E. Multiple chiral topological states in liquid crystals from unstructured light beams. Appl. Phys. Lett. 2014, 104, 051911. [Google Scholar] [CrossRef] [Green Version]
- Loussert, C.; Iamsaard, S.; Katsonis, N.; Brasselet, E. Subnanowatt opto-molecular generation of localized defects in chiral liquid crystals. Adv. Mater. 2014, 26, 4242. [Google Scholar] [CrossRef] [Green Version]
- Tai, J.S.B.; Smalyukh, I.I. Surface anchoring as a control parameter for stabilizing torons, skyrmions, twisted walls, fingers and their hybrids in chiral nematics. Phys. Rev. E 2020, 101, 042702. [Google Scholar] [CrossRef]
- Hess, A.J.; Poy, G.; Tai, J.S.B.; Žumer, S.; Smalyukh, I.I. Control of light by topological solitons in soft chiral birefringent media. Phys. Rev. X 2020, 10, 031042. [Google Scholar] [CrossRef]
- Nys, I.; Chen, K.; Beeckman, J.; Neyts, K. Periodic planar-homeotropic anchoring realized by photoalignment for stabilization of chiral superstructures. Adv. Opt. Mater. 2018, 6, 1701163. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals, 2nd ed.; Oxford University Press: Oxford, UK, 1993; pp. 76–78. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M.; Pitaevskii, L.P. Statistical Physics, 3rd ed.; Pergamon Press: Oxford, UK, 1980; pp. 440–442. [Google Scholar]
- James, R.; Willman, E.; Fernández, F.A.; Day, S.E. Finite-Element Modeling of Liquid-Crystal Hydrodynamics with a Variable Degree of Order. IEEE Trans. Electron. Devices 2006, 53, 1575–1582. [Google Scholar] [CrossRef]
- Willman, E.; Fernández, F.A.; James, R.; Day, S.E. Modeling of weak anisotropic anchoring of nematic liquid crystals in the Landau-de Gennes theory. IEEE Trans. Electron. Devices 2007, 54, 2630–2637. [Google Scholar] [CrossRef]
- Willman, E.; Fernández, F.A.; James, R.; Day, S.E. Switching Dynamics of a Post-Aligned Bistable Nematic Liquid Crystal Device. J. Display Technol. 2008, 4, 276–281. [Google Scholar] [CrossRef]
- James, R.; Fernández, F.A.; Day, S.E.; Bulja, S.; Mirshekar-Syahkal, D.; Yazdanpanahi, M. Finite Element Analysis of a Balanced Microstrip Line Filled with Nematic Liquid Crystal. In Proceedings of the 2009 IEEE MTT-S International Microwave Symposium Digest, Boston, MA, USA, 7–12 June 2009; Volume 1–3, pp. 133–136. [Google Scholar] [CrossRef]
- Poy, G.; Žumer, S. Physics-based multistep beam propagation in inhomogeneous birefringent media. Optics Express 2020, 28, 24327–24341. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; McGinty, C.; West, J.; Bryant, D.; Finnemeyer, V.; Reich, R.; Berry, S.; Clark, H.; Yaroshchuk, O.; Bos, P. Effects of humidity and surface on photoalignment of brilliant yellow. Liq. Cryst. 2016, 44, 863–872. [Google Scholar] [CrossRef]
- Yaroshchuk, O.; Hegde, G.; Chigrinov, V.G.; Kwok, H.; Hasebe, H.; Takatsu, H. Photoalignment properties of brilliant yellow dye. In Proceedings of the 14th International Display Workshops, IDW ’07, Sapporo, Japan, 5–7 December 2007; pp. 1665–1668. [Google Scholar]
- Finnemeyer, V.; Bryant, D.; Bos, P. 67.1: Reactive mesogen stabilized azodye alignment for high-contrast displays. In Proceedings of the SID Symposium Digest of Technical Papers, San Jose, CA, USA, 21 May–5 June 2015; Volume 46, pp. 991–993. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics, 3rd ed.; Roberts and Company Publishers: Englewood, CO, USA, 2005. [Google Scholar]












© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nys, I.; Berteloot, B.; Poy, G. Surface Stabilized Topological Solitons in Nematic Liquid Crystals. Crystals 2020, 10, 840. https://doi.org/10.3390/cryst10090840
Nys I, Berteloot B, Poy G. Surface Stabilized Topological Solitons in Nematic Liquid Crystals. Crystals. 2020; 10(9):840. https://doi.org/10.3390/cryst10090840
Chicago/Turabian StyleNys, Inge, Brecht Berteloot, and Guilhem Poy. 2020. "Surface Stabilized Topological Solitons in Nematic Liquid Crystals" Crystals 10, no. 9: 840. https://doi.org/10.3390/cryst10090840
APA StyleNys, I., Berteloot, B., & Poy, G. (2020). Surface Stabilized Topological Solitons in Nematic Liquid Crystals. Crystals, 10(9), 840. https://doi.org/10.3390/cryst10090840