Contact-Mediated Nucleation of Subcooled Droplets in Melt Emulsions: A Microfluidic Approach
Abstract
:1. Introduction
1.1. Contact-Mediated Nucleation
1.2. Microfluidics
1.3. Theoretical Description of Contact-Mediated Nucleation—An Approach
2. Materials and Methods
2.1. Materials Used
2.2. Microfluidic Measurement Setup
2.3. Melting Point Measurements
2.4. Specific Interfacial Energy Measurements
2.5. Wetting
3. Results
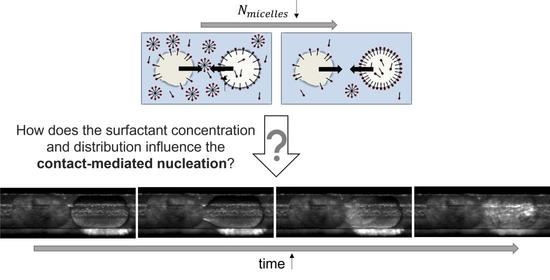
3.1. Surfactant Distribution between the Water and Oil Phase and the Liquid-Liquid Interface
3.2. Effect of Tween®20 Distribution on Contact-Mediated Nucleation
3.3. Formation of Liquid Bridges before Contact-Mediated Nucleation
3.4. Induction Time
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bancroft, W.D. The Theory of Emulsification, V. J. Phys. Chem. 1913, 17, 501–519. [Google Scholar] [CrossRef] [Green Version]
- Sharma, M.K.; Shah, D.O. Introduction to Macro- and Microemulsions. In Proceedings of the ACS Symposium Series; American Chemical Society (ACS): Washington, DC, USA, 1985; Volume 28, pp. 1–18. [Google Scholar]
- Tadros, T.F. Emulsion Formation, Stability, and Rheology. In Emulsion Formation and Stability; Tadros, T.F., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013; pp. 1–75. [Google Scholar]
- Rosen, M.J.; Kunjappu, J.T. Surfactants and Interfacial Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 1–38. [Google Scholar]
- Lauth, G.J.; Kowalczyk, J. Einführung in die Physik und Chemie der Grenzflächen und Kolloide; Springer Spektrum: Heidelberg/Berlin, Germany, 2016; pp. 53–89. [Google Scholar]
- Callen, H.B. Thermodynamics And An Introduction To Thermostatics; John Wiley & Sons: New York, NY, USA, 1985; pp. 35–58. [Google Scholar]
- Nernst, W. Ueber die Berechnung chemischer Gleichgewichte aus thermischen Messungen. Nachr. Ges. Wiss. Göttingen Math. Phys. Kl. 1906, 1906, 1–40. [Google Scholar]
- McClements, J.D.; Dickinson, E.; Povey, M. Crystallization in hydrocarbon-in-water emulsions containing a mixture of solid and liquid droplets. Chem. Phys. Lett. 1990, 172, 449–452. [Google Scholar] [CrossRef]
- McClements, D.J.; Dungan, S.R. Effect of Colloidal Interactions on the Rate of Interdroplet Heterogeneous Nucleation in Oil-in-Water Emulsions. J. Colloid Interface Sci. 1997, 186, 17–28. [Google Scholar] [CrossRef] [PubMed]
- Dickinson, E.; Kruizenga, F.-J.; Povey, M.J.; van der Molen, M. Crystallization in oil-in-water emulsions containing liquid and solid droplets. Colloids Surf. A Physicochem. Eng. Asp. 1993, 81, 273–279. [Google Scholar] [CrossRef]
- Hindle, S.A.; Povey, M.J.W.; Smith, K. Kinetics of Crystallization in n-Hexadecane and Cocoa Butter Oil-in-Water Emulsions Accounting for Droplet Collision-Mediated Nucleation. J. Colloid Interface Sci. 2000, 232, 370–380. [Google Scholar] [CrossRef]
- Dudek, M.; Fernandes, D.; Helno Herø, E.; Øye, G. Microfluidic method for determining drop-drop coalescence and contact times in flow. Colloids Surf. A Physicochem. Eng. Asp. 2019, 586, 124265. [Google Scholar] [CrossRef]
- Basheva, E.S.; Kralchevsky, P.A.; Danov, K.D.; Ananthapadmanabhan, K.P.; Lips, A. The colloid structural forces as a tool for particle characterization and control of dispersion stability. Phys. Chem. Chem. Phys. 2007, 9, 5183–5198. [Google Scholar] [CrossRef] [PubMed]
- Vanapalli, S.A.; Coupland, J.N. Orthokinetic Stability of Food Emulsions. In Food Emulsions; Friberg, S., Ed.; CRC Press: Boca Raton, FL, USA, 2003; pp. 327–352. [Google Scholar]
- Kaysan, G.; Schork, N.; Herberger, S.; Guthausen, G.; Kind, M. Contact-mediated nucleation in melt emulsions investigated by Rheo-NMR. Magn. Reson. Chem. 2021. [Google Scholar] [CrossRef]
- Chesters, A. The modelling of coalescence processes in fluid-liquid dispersions: A review of current understanding. Chem. Eng. Res. Des. 1991, 69, 259–270. [Google Scholar]
- Bremond, N.; Bibette, J. Exploring emulsion science with microfluidics. Soft Matter 2012, 8, 10549–10559. [Google Scholar] [CrossRef]
- Puigmartí-Luis, J. Microfluidic platforms: A mainstream technology for the preparation of crystals. Chem. Soc. Rev. 2013, 43, 2253–2271. [Google Scholar] [CrossRef] [PubMed]
- Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef] [PubMed]
- Muijlwijk, K.; Berton-Carabin, C.; Schroën, K. Cross-flow microfluidic emulsification from a food perspective. Trends Food Sci. Technol. 2016, 49, 51–63. [Google Scholar] [CrossRef]
- Schroën, K.; Bliznyuk, O.; Muijlwijk, K.; Sahin, S.; Berton-Carabin, C.C. Microfluidic emulsification devices: From micrometer insights to large-scale food emulsion production. Curr. Opin. Food Sci. 2015, 3, 33–40. [Google Scholar] [CrossRef]
- Won, J.Y.; Krägel, J.; Makievski, A.V.; Javadi, A.; Gochev, G.; Loglio, G.; Pandolfini, P.; Leser, M.E.; Gehin-Delval, C.; Miller, R. Drop and bubble micro manipulator (DBMM)—A unique tool for mimicking processes in foams and emulsions. Colloids Surf. A Physicochem. Eng. Asp. 2013, 441, 807–814. [Google Scholar] [CrossRef]
- Dickinson, E.; Murray, B.S.; Stainsby, G. Coalescence stability of emulsion-sized droplets at a planar oil–water interface and the relationship to protein film surface rheology. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1988, 84, 871–883. [Google Scholar] [CrossRef]
- Neumann, S.M.; van der Schaaf, U.S.; Karbstein, H.P. Investigations on the relationship between interfacial and single droplet experiments to describe instability mechanisms in double emulsions. Colloids Surf. A Physicochem. Eng. Asp. 2018, 553, 464–471. [Google Scholar] [CrossRef]
- Taboada, M.; Leister, N.; Karbstein, H.P.; Gaukel, V. Influence of the Emulsifier System on Breakup and Coalescence of Oil Droplets during Atomization of Oil-In-Water Emulsions. ChemEngineering 2020, 4, 47. [Google Scholar] [CrossRef]
- Shinnar, R.; Church, J.M. Statistical Theories of Turbulence in Predicting Particle Size in Agitated Dispersions. Ind. Eng. Chem. 1960, 52, 253–256. [Google Scholar] [CrossRef]
- Verwey, E.J.W. Theory of the stability of lyophobic colloids. J. Phys. Colloid Chem. 1947, 51, 631–636. [Google Scholar] [CrossRef] [Green Version]
- Derjaguin, B.; Landau, L. Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes. Prog. Surf. Sci. 1993, 43, 30–59. [Google Scholar] [CrossRef]
- Fuchs, N. Über die Stabilität und Aufladung der Aerosole. Eur. Phys. J. A 1934, 89, 736–743. [Google Scholar] [CrossRef]
- Dimitrova, T.D.; Leal-Calderon, F. Forces between Emulsion Droplets Stabilized with Tween 20 and Proteins. Langmuir 1999, 15, 8813–8821. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Burlington, MA, USA, 2011; pp. 191–499. [Google Scholar]
- Trokhymchuk, A.; Henderson, D.; Nikolov, A.; Wasan, D.T. A Simple Calculation of Structural and Depletion Forces for Fluids/Suspensions Confined in a Film. Langmuir 2001, 17, 4940–4947. [Google Scholar] [CrossRef]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminform. 2012, 4, 17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chou, W.-L.; Lee, P.-Y.; Yang, C.-L.; Huang, W.-Y.; Lin, Y.-S. Recent Advances in Applications of Droplet Microfluidics. Micromachines 2015, 6, 1249–1271. [Google Scholar] [CrossRef] [Green Version]
- Angeli, P.; Gavriilidis, A. Hydrodynamics of Taylor flow in small channels: A Review. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci. 2008, 222, 737–751. [Google Scholar] [CrossRef]
- Baroud, C.N.; Gallaire, F.; Dangla, R. Dynamics of microfluidic droplets. Lab Chip 2010, 10, 2032–2045. [Google Scholar] [CrossRef] [Green Version]
- Musterd, M.; van Steijn, V.; Kleijn, C.R.; Kreutzer, M.T. Calculating the volume of elongated bubbles and droplets in microchannels from a top view image. RSC Adv. 2015, 5, 16042–16049. [Google Scholar] [CrossRef] [Green Version]
- Selzer, D.; Spiegel, B.; Kind, M. A Generic Polycarbonate Based Microfluidic Tool to Study Crystal Nucleation in Microdroplets. J. Cryst. Process. Technol. 2018, 8, 1–17. [Google Scholar] [CrossRef] [Green Version]
- McClements, D.; Dungan, S.; German, J.; Simoneau, C.; Kinsella, J. Droplet Size and Emulsifier Type Affect Crystallization and Melting of Hydrocarbon-in-Water Emulsions. J. Food Sci. 1993, 58, 1148–1151. [Google Scholar] [CrossRef]
- Vélez, C.; Khayet, M.; Ortiz de Zárate, J.M. Temperature-dependent thermal properties of solid/liquid phase change even-numbered n-alkanes: N-Hexadecane, n-octadecane and n-eicosane. Appl. Energy 2015, 143, 383–394. [Google Scholar] [CrossRef]
- Zou, G.L.; Tan, Z.C.; Lan, X.Z.; Sun, L.X.; Zhang, T. Preparation and characterization of microencapsulated hexadecane used for thermal energy storage. Chin. Chem. Lett. 2004, 15, 729–732. [Google Scholar]
- González, J.A.; Zawadzki, M.; Domanska, U. Thermodynamics of mixtures containing polycyclic aromatic hydrocarbons. J. Mol. Liq. 2008, 143, 134–140. [Google Scholar] [CrossRef]
- Zhang, P.; Ma, Z.; Wang, R. An overview of phase change material slurries: MPCS and CHS. Renew. Sustain. Energy Rev. 2010, 14, 598–614. [Google Scholar] [CrossRef]
- Spiegel, B.; Käfer, A.; Kind, M. Crystallization Behavior and Nucleation Kinetics of Organic Melt Droplets in a Microfluidic Device. Cryst. Growth Des. 2018, 18, 3307–3316. [Google Scholar] [CrossRef]
- Schroën, K.; de Ruiter, J.; Berton-Carabin, C. The Importance of Interfacial Tension in Emulsification: Connecting Scaling Relations Used in Large Scale Preparation with Microfluidic Measurement Methods. ChemEngineering 2020, 4, 63. [Google Scholar] [CrossRef]
- Hashimoto, M.; Garstecki, P.; Stone, H.A.; Whitesides, G.M. Interfacial instabilities in a microfluidic Hele-Shaw cell. Soft Matter 2008, 4, 1403–1413. [Google Scholar] [CrossRef] [PubMed]
- van der Graaf, S.; Schroën, C.G.P.H.; van der Sman, R.G.M.; Boom, R.M. Influence of dynamic interfacial tension on droplet formation during membrane emulsification. J. Colloid Interface Sci. 2004, 277, 456–463. [Google Scholar] [CrossRef]
- Miller, R.; Aksenenko, E.; Fainerman, V. Dynamic interfacial tension of surfactant solutions. Adv. Colloid Interface Sci. 2017, 247, 115–129. [Google Scholar] [CrossRef]
- Tween®20; Safety Data Sheet for Tween® 20 (Polysorbat) 817072 [Online]; MERCK: Darmstadt, Germany, 5 December 2020; Available online: https://www.merckmillipore.com/DE/de/product/msds/MDA_CHEM-817072 (accessed on 31 May 2021).
- Tween®20; Product Information on Polyoxyethylenesorbitan Monolaurate (Tween20) [Online]; Sigma Aldrich: St. Louis, MO, USA, 29 July 2021; Available online: https://www.sigmaaldrich.com/content/dam/sigma-aldrich/docs/Sigma/Product_Information_Sheet/1/p6585pis.pdf (accessed on 24 November 2021).
- Pollard, J.M.; Shi, A.J.; Göklen, K.E. Solubility and Partitioning Behavior of Surfactants and Additives Used in Bioprocesses. J. Chem. Eng. Data 2006, 51, 230–236. [Google Scholar] [CrossRef]
- Jin, F.; Balasubramaniam, R.; Stebe, K.J. Surfactant Adsorption to Spherical Particles: The Intrinsic Length Scale Governing the Shift from Diffusion to Kinetic-Controlled Mass Transfer. J. Adhes. 2004, 80, 773–796. [Google Scholar] [CrossRef]
- Staszak, M. A Linear Diffusion Model of Adsorption Kinetics at Fluid/Fluid Interfaces. J. Surfactants Deterg. 2016, 19, 297–314. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chanamai, R.; McClements, D. Isothermal titration calorimetry measurement of enthalpy changes in monodisperse oil-in-water emulsions undergoing depletion flocculation. Colloids Surf. A Physicochem. Eng. Asp. 2001, 181, 261–269. [Google Scholar] [CrossRef]
- Helenius, A.; McCaslin, D.R.; Fries, E.; Tanford, C. Properties of detergents. In Biomembranes Part G: Bioenergetics: Biogenesis of Mitochondria, Organization, and Transport; Kaplan, N.P., Colowick, N.P., Fleischer, S., Sies, H., Eds.; Elsevier: Amsterdam, The Netherlands, 1979; pp. 734–749. [Google Scholar]
- Bera, B.; Khazal, R.; Schroën, K. Coalescence dynamics in oil-in-water emulsions at elevated temperatures. Sci. Rep. 2021, 11, 1–10. [Google Scholar] [CrossRef]
- Nowak, E.; Kovalchuk, N.; Che, Z.; Simmons, M. Effect of surfactant concentration and viscosity of outer phase during the coalescence of a surfactant-laden drop with a surfactant-free drop. Colloids Surf. A Physicochem. Eng. Asp. 2016, 505, 124–131. [Google Scholar] [CrossRef] [Green Version]
- Scriven, L.E.; Sterling, C.V. The Marangoni Effects. Nature 1960, 187, 186–188. [Google Scholar] [CrossRef]
- Schuchmann, H.P.; Danner, T. Emulgieren: Mehr als nur Zerkleinern. Chemie Ingenieur Technik 2004, 76, 364–375. [Google Scholar] [CrossRef]
- Köhler, K.; Hensel, A.; Kraut, M.; Schuchmann, H.P. Melt emulsification—Is there a chance to produce particles without additives? Particuology 2011, 9, 506–509. [Google Scholar] [CrossRef]
- Chen, J.-D.; Hahn, P.S.; Slattery, J.C. Coalescence time for a small drop or bubble at a fluid-fluid interface. AIChE J. 1984, 30, 622–630. [Google Scholar] [CrossRef]
- Mackay, G.D.M.; Mason, S.G. The gravity approach and coalescence of fluid drops at liquid interfaces. Can. J. Chem. Eng. 1963, 41, 203–212. [Google Scholar] [CrossRef]
- Hodgson, T.; Woods, D. The effect of surfactants on the coalescence of a drop at an interface. II. J. Colloid Interface Sci. 1969, 30, 429–446. [Google Scholar] [CrossRef]
- Leister, N.; Karbstein, H.P. Influence of Hydrophilic Surfactants on the W1–W2 Coalescence in Double Emulsion Systems Investigated by Single Droplet Experiments. Colloids Interfaces 2021, 5, 21. [Google Scholar] [CrossRef]
- Christov, N.C.; Danov, K.D.; Zeng, Y.; Kralchevsky, P.A.; von Klitzing, R. Oscillatory Structural Forces Due to Nonionic Surfactant Micelles: Data by Colloidal-Probe AFM vs. Theory. Langmuir 2010, 26, 915–923. [Google Scholar] [CrossRef] [PubMed]
- Hsu, J.-P.; Nacu, A. Behavior of soybean oil-in-water emulsion stabilized by nonionic surfactant. J. Colloid Interface Sci. 2003, 259, 374–381. [Google Scholar] [CrossRef]
- Hammer, M.U.; Anderson, T.H.; Chaimovich, A.; Shell, M.S.; Israelachvili, J. The search for the hydrophobic force law. Faraday Discuss. 2010, 146, 299–308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meyer, E.E.; Rosenberg, K.J.; Israelachvili, J. Recent progress in understanding hydrophobic interactions. Proc. Natl. Acad. Sci. USA 2006, 103, 15739–15746. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhu, Y.; Granick, S. Softened hydrophobic Attraction between Macroscopic Surfaces in Relative Motion. J. Am. Chem. Soc. 2001, 123, 6736–6737. [Google Scholar] [CrossRef]
- Singh, S.; Houston, J.; van Swol, F.; Brinker, C.J. Superhydrophobicity: Drying transition of confined water. Nature 2006, 442, 526. [Google Scholar] [CrossRef]
- Krawczyk, M.A.; Wasan, D.T.; Shetty, C. Chemical demulsification of petroleum emulsions using oil-soluble demulsifiers. Ind. Eng. Chem. Res. 1991, 30, 367–375. [Google Scholar] [CrossRef]
- Opawale, F.O.; Burgess, D.J. Influence of Interfacial Properties of Lipophilic Surfactants on Water-in-Oil Emulsion Stability. J. Colloid Interface Sci. 1998, 197, 142–150. [Google Scholar] [CrossRef] [PubMed]
- Muijlwijk, K.; Colijn, I.; Harsono, H.; Krebs, T.; Berton-Carabin, C.; Schroën, K. Coalescence of protein-stabilised emulsions studied with microfluidics. Food Hydrocoll. 2017, 70, 96–104. [Google Scholar] [CrossRef]














| Parameter | Value |
|---|---|
| Micelle diameter of Tween®20 [13] | |
| Radius n-hexadecane droplet in the microfluidic device | |
| Temperature | 290.35 K |
| Length of emulsifier’s brush layer (determined by Avogardo, Version 1.2.0 [33]) | |
| Hamaker constant for an emulsion system [13] | J |
| 8.2 | 3.5 ± 0.3 |
| 16.6 | 2.9 ± 0.2 |
| 6.4 | 1.9 ± 0.4 |
| 12.9 | 0.9 ± 0.3 |
| Wetting Angle | Nucleation? | Wetting? | Abstraction | Experimental |
|---|---|---|---|---|
| φ = 180°, blank | no | no |  |  |
| φ = 0°, hug | yes | not initially |  |  |
| 0° < φ < 180° | yes | yes |  |  |
| φ = 0° | yes | yes |  |  |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaysan, G.; Rica, A.; Guthausen, G.; Kind, M. Contact-Mediated Nucleation of Subcooled Droplets in Melt Emulsions: A Microfluidic Approach. Crystals 2021, 11, 1471. https://doi.org/10.3390/cryst11121471
Kaysan G, Rica A, Guthausen G, Kind M. Contact-Mediated Nucleation of Subcooled Droplets in Melt Emulsions: A Microfluidic Approach. Crystals. 2021; 11(12):1471. https://doi.org/10.3390/cryst11121471
Chicago/Turabian StyleKaysan, Gina, Alexander Rica, Gisela Guthausen, and Matthias Kind. 2021. "Contact-Mediated Nucleation of Subcooled Droplets in Melt Emulsions: A Microfluidic Approach" Crystals 11, no. 12: 1471. https://doi.org/10.3390/cryst11121471
APA StyleKaysan, G., Rica, A., Guthausen, G., & Kind, M. (2021). Contact-Mediated Nucleation of Subcooled Droplets in Melt Emulsions: A Microfluidic Approach. Crystals, 11(12), 1471. https://doi.org/10.3390/cryst11121471