3.1. Multi-Grained Materials
Figure 2 shows the PXRD patterns of samples I, II and III after being annealed at 990 °C for 240 h. The intensities are drawn on a logarithmic scale to enhance the weakest peaks. Therefore, the background noise, mostly visible at high Bragg angles, exhibited a relative increase when relating it to the adjacent low-intensity peaks. The PXRD patterns revealed the presence of five different intermetallic compounds. All the diffraction peaks were sharply defined Bragg peaks. They were deconvoluted into separated patterns and subsequently indexed using the PDF4+ database. The AlCr
2 compound crystallises in the MoSi
2 tetragonal structure type with space group I4/mmm and lattice parameters a = 0.29984 nm and c = 0.86303 nm [
25]. Al
3Sc has the space group Pm-3m, with a cubic structure and a lattice parameter a = 0.41030 nm [
26]. Al
3Cr
7 has the space group Im-3m and a lattice parameter a = 0.30000 nm [
27]. The φ-Al
8Cr
4Sc ternary phase [
3] belongs to the Al
8Cr
4RE prototype crystal structure, which crystallises in the tetragonal structure type with space group I4/mmm and lattice parameters a = 0.88557 nm and c = 0.50970 nm. The fifth compound is the ternary phase, which was the focus of our research.
The PXRD pattern of sample I (
Figure 2a) showed that four intermetallic compounds coexisted in the specimen: the φ-Al
8Cr
4Sc ternary phase, two binary phases with compositions AlCr
2 and Al
3Sc and a predominant phase with a hexagonal crystal structure of a MgZn
2 prototype that we called Al
2−xCr
xSc for reasons that are explained later in this article. This particular hexagonal crystal structure in the Al-Cr-Sc system was first identified from SCXRD data by Radzieowski et al. [
4], but with a different composition, i.e., a different Al/Cr ratio, when compared with our system.
Sample II (
Figure 2b) consisted of the binary Al
3Cr
7 phase [
27] and the Al
2−xCr
xSc crystal structure, in addition to a tiny amount of AlCr
2 and Al
8Cr
4Sc. In sample III (
Figure 2c), the Al
2−xCr
xSc crystal structure was identified as the dominant phase with the highest peak intensity, together with the binary phase AlCr
2 in a smaller amount. These results indicated that the Al
2−xCr
xSc compound was stable in all three samples.
The SEM/BSE images for the three annealed samples provided a direct microstructural comparison of the alloys (
Figure 3a,c,e). These images were taken from the central areas of the samples. The contrast variations in the SEM/BSE images due to the atomic number Z-contrast indicated the existence of different phases with different chemical compositions. Several quantitative EDXS point-beam analyses were systematically performed on grains with different grey levels to extract the chemical compositions of the phases with high statistical confidence. The detailed chemical compositions of the samples, grain size distributions and prototype crystal structures are presented in
Table 2. All the identified phases are marked in the high-magnification SEM/BSE micrographs (
Figure 3b,d,f): φ-Al
8Cr
4Sc, AlCr
2, Al
3Sc, Al
3Cr
7 and Al
2−xCr
xSc.
The dominant phase was analysed first in all three samples. In sample I (
Figure 3a,b), a binary eutectic (φ-Al
8Cr
4Sc + Al
2−xCr
xSc) was formed with a morphology that was typical of a normal eutectic (eutectic cell or rod-like structures). The Al
3Sc and AlCr
2 compounds were minor phases with volumes that were smaller than the analytical interaction volumes for the EDXS analysis. It should be noted that determining the exact chemical composition of these two phases using EDXS was very difficult because of the relatively small analysed grains when compared with the analytical interaction volume for the EDXS in the SEM, leading to the partial signal formation from the surrounding or neighbouring phases. As a result, the assigned phases were deduced by combining the EDXS and PXRD data with the SEM/BSE images.
The microstructure of the binary eutectic (Al
3Cr
7 + Al
2−xCr
xSc) also had the typical morphology of rod-like eutectics in sample II and is visible in
Figure 3c,d. The predominant Al
2−xCr
xSc phase, along with the particles of the AlCr
2 phase in sample III, are easily identified in
Figure 3e,f. The average composition of the Al
2−xCr
xSc phase corresponded to Al 53.0 ± 0.5 at%, Cr 13.2 ± 0.3 at% and Sc 33.8 ± 0.3 at% and it departed slightly from these figures in the other two samples. This phase was attributed to a MgZn
2 prototype compound with a chemical formula Al
2−xCr
xSc, where x varied between 0.4 and 0.5. The estimated volume fraction of the Al
2−xCr
xSc phase was the largest in sample III, and this sample was used in the subsequent experimental characterisations.
Figure 4 presents the DSC curves of a pristine fragment of the arc-melted sample III with a nominal composition of Al
52Cr
14Sc
34. DSC was used to investigate the thermal stability of the phases under flowing Ar in the range 24–1500 °C during heating and cooling at a rate of 3 °C/min.
The DSC experiments revealed that both the heating and cooling curves featured three major peaks, as marked in
Figure 4. The beginning of each of the most noticeable peaks is marked with an arrow, accompanied by the corresponding initial temperature. It was observed (
Figure 4) that the liquidus temperature was 1397 ± 1 °C where the primary crystallisation of the Al
2−xCr
xSc phase began. The solidus lay at 1141 °C where the peritectic formation of the Al
3Sc phase [
26] started. It was followed by the peritectic formation of the AlCr
2 [
28] phase at 1124 °C.
The metallographic analysis (inset in
Figure 4) showed the existence of three different phases. The results of the EDXS analyses of the sample after the DSC experiment are presented in
Table 3. They were consistent with those that were already observed in the same sample III after being annealed at 990 °C for 240 h (
Table 2). The sample after the DSC analysis was further checked using the PXRD technique, which confirmed that all the phases were identical to the phases that were observed in the annealed sample. A tiny amount of a few wt% of the AlCr
2 phase could be detected thanks to its most intense peak, as shown by an arrow in
Figure 5. Lines due to other compounds were too weak to be observed.
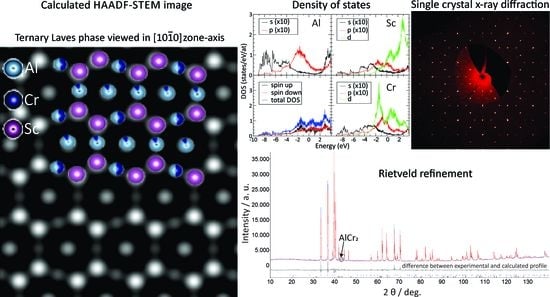
The structure refinement was initiated with an approximate model based on the two AlCr2 and Al2–xCrxSc phases that were clearly identified in the annealed sample III. The structures were refined using TOPAS (full-matrix least square) with isotropic atomic displacement parameters for all the atoms. The confirmation of the crystal structures was assessed using a Rietveld refinement. The final refinements were carried out using the atomic occupancy, leading to a final reliability factor of Rwp = 4.18% and RBragg = 2.30%. The dimensions of the Al2–xCrxSc hexagonal unit cell thus obtained were a = 0.533993(2) nm and c = 0.862609(5) nm.
According to the single-crystal refinement, as explained below, final refinements for all the atomic positions showed a mixed occupation at the Al/Cr sites with 0.37/0.63 for Cr (1)/Al (1) and 0.89/0.11 for Al (2)/ Cr (2). The final reliability factor was Rwp = 4.18%. The calculated composition from the powder Rietveld refinement data was Al
54.9Cr
11.8Sc
33.3 (at%). As mentioned in
Figure 2c, the diffraction peak that was observed at 2θ = 43.48° was assigned to AlCr
2, leading to the tetragonal lattice parameters a = 0.3014 nm and b = 0.8656 nm according to the MoSi
2 type of structure mentioned in the literature.
3.2. Single Grain Sample
To obtain reliable crystallographic data, a single crystal with approximate dimensions of 15 μm × 20 μm × 20 μm as extracted by mechanical grinding from sample III, which was essentially formed of the Al
2–xCr
xSc phase. It was studied using SCXRD at room temperature.
Figure 6 presents SCXRD precession patterns in two low-index zones of the ternary phase and the corresponding crystal structure when moving along the
zone axis.
The crystallographic data and positional parameters using the program Structure Tidy [
29] for the single crystal are listed in
Table 4. The atomic coordinates and isotropic and anisotropic displacement parameters are gathered in
Table 5 in comparison with single-crystal refinement data. The corresponding crystallographic information file (CIF) of the ternary Laves phase (see next sub-section) can be found in the
Supplementary Materials section.
The ternary compound crystallised with a hexagonal close-packed unit cell, with a = 0.53424(2) nm and c = 0.86302(3) nm, space group no. 194 P63/mmc. Direct methods were used to define the positions of the independent atoms: Sc (1) in (4f), Cr (1) and Al (1) in (2a), Cr (2) in (6h) and Al (2) in (6h). A mixed occupation at the Al/Cr sites with 0.528/0.472 for Cr (1)/Al (1) and 0.886/0.114 for Al (2)/Cr (2) was confirmed after the final refinements, including occupation factors for all the atoms. No other mixed occupancy was observed. The final reliability factors were R1 = 2.23% and wR2 = 3.57%. After the final refinement of the single crystal, the composition of the investigated crystal was Al53.3Cr13.3Sc33.3 (at%).
3.3. Site Occupancy
It was observed from the PXRD and SCXRD measurements that the Al-Cr-Sc ternary phase was characterised by the coexistence of all three elements, namely, Al, Cr and Sc, and it belonged to the prototype structure MgZn2, which is a well-known Laves phase. The crystal structure was hexagonal with the space group P63/mmc and lattice parameters a = 0.53424(2) nm and c = 0.86302(3) nm from the single crystal data and a = 0.533993(2) nm and c = 0.862609(5) nm from the powder refinement. From both diffraction methods, the Wyckoff site 4f had full Sc occupancy. The Rietveld refinement from the polycrystalline sample indicated a mixed occupancy of both Al Wyckoff sites: for site 2a with a ratio of 0.64 Al to 0.36 Cr and site 6h with a ratio of 0.89 Al to 0.11 Cr. From the extracted single crystal, the mixed occupancy of both sites was 0.53 Al/0.47 Cr for site 2a and 0.89 Al/0.11 Cr for site 6h. The calculated composition from single-crystal diffraction was Al53.3Cr13.3Sc33.3 (at%) and from the powder, it was Al54.9Cr11.8Sc33.3 (at%). The difference between the occupancy ratios at site 2a confirmed the slight homogeneity that was observed by EDXS for this phase.
SAED pattern analysis combined with high-resolution HAADF-STEM imaging was performed to verify the predicted crystal structure of the Al-Cr-Sc ternary phase at an atomic scale.
Figure 7a shows the experimental SAED patterns that were acquired along the
zone axis, exposing both the basal
and prism
principal planes of the analysed hexagonal ternary phase. The measured lattice parameters for the given basal and prism set of planes were 0.87 nm and 0.46 nm, which is in excellent agreement with the corresponding theoretical values of 0.863 nm and 0.462 nm, respectively.
An experimental atomic resolution HAADF-STEM image that was acquired from the same specimen region as the SAED pattern of
Figure 7a is shown in
Figure 7b. Experimental images were processed by applying a low-frequency filter to reduce the slowly varying intensity extending over the large image section well beyond the individual atomic columns. For clarity, the original experimental image is shown as an inset in the left-side part of the figure. As the contrast variation in the atomic resolution HAADF-STEM images roughly followed a Z
2 dependence on the average atomic number Z, small compositional differences in the probed atomic columns are reflected in significant contrast variations. The observed image intensity could be characterised by two sets of basal planes (B) with an undulated appearance, separated by flat planes (F), as marked in
Figure 7c. The undulated planes are mirrored over the flat planes, following the predicted atomic model of the ternary phase (
Figure 7c). A detailed analysis of the intensity variations within the undulated planes shows a periodic arrangement of two bright spots that were intercalated with a spot of slightly weaker intensity. According to the predicted model, the highest-intensity spots corresponded to a pair of Sc (Z = 21) columns, which were intercalated with a mixed Al(13)-Cr(24) column. Here, 47% of the Al sites were replaced by Cr atoms (from here on denoted as the 2a site), which was in fair agreement with the observed intensity variations. The intensity variation within the flat plane showed a periodic exchange of high-intensity spots with spots of very low intensity (marked by arrows). According to the predicted structure model, the atomic columns of the flat plane all had the same composition, namely, Al-Cr mixed with 11.4% of Al exchanged by Cr atoms (6h-site), which was not directly evident from the corresponding experimental observation. This can be explained by the fact that the projected atomic density within the individual Al-Cr mixed atomic columns was different, which had a direct impact on the observed signal intensity. Namely, within a unit cell, the 6h sites were characterised by a single-atom site, namely, 6h-I, that was exchanged with two-atom sites, namely, 6h-II, when the atomic columns were observed in the
viewing direction. In other words, the projected atomic density within the flat planes periodically oscillated between neighbouring columns, thus explaining the observed intensity oscillations.
The HAADF-STEM image simulations were performed to quantify the observed intensity variations as a function of the mixed occupancies that were predicted by the structural model, as shown in
Figure 7d. The overall arrangement of the atomic columns, as revealed by the simulated image, agreed with the experimental observation. Furthermore, the relative intensity differences within the undulated planes between the Sc 4f and Al/Cr 2a sites and within the flat planes followed similar trends to the experimental image. Small differences between the simulation and experiment could be found by comparing the relative intensity variations between the 2a and 6h-II sites, where the experimentally observed intensities at the 6h-I sites were higher than those predicted by the model. This result suggested that the amount of Cr was not entirely fixed to the given Al sites and could be locally changed, which partially explained the small differences in the composition between the EDXS and the single-crystal diffraction analyses.
The symmetry of the neighbourhood around the 2a Al/Cr sites in (0,0,0) and (0, 0, 0.5) is shown in
Figure 8a,b, respectively. It consisted of a perfect icosahedron made of six (6h) Al/Cr and six Sc atoms, which were connected by sharing an edge of two Sc atoms located in the (a, b) plane and a triangular facet of three Al/Cr atoms along the c axis. This specific configuration enforced the a = b = c/τ relationship, where τ = (1 + √5)/2 is the golden ratio. Like in other Laves phases, icosahedral order was therefore dominant in this Al-Cr-Sc compound. It also extended to the next-nearest neighbours of the 6h Al/Cr atoms, which was a pentagonal dodecahedron of atoms that were located at distances of 0.32 and 0.49 nm (
Figure 8c).
3.4. Computed Structure and Density of Electronic States
According to
Table 5, the crystal structure of the Al
2–xCr
xSc compound contained positions with mixed occupancies. Such disorder was not straightforward to implement within our modelling method based on periodic boundary conditions. Indeed, the previous long-range vision had no physical relevance at the local level, where two atoms could not occupy the same physical position. As a consequence, large ordered supercells were used here, followed by configurational averaging, as detailed below [
30].
Using a supercell generally implies a study of numerous atomic configurations. Before starting an extensive exploration of possible crystal structures, we first built a model by assuming that the 6h position was fully occupied by Al atoms. The input structure was built starting from the MgZn
2 type (P63/mmc). Six Al and four Sc atoms were positioned in 6h and 4f sites, respectively. According to the experimental study, the 2a sites had a mixed occupancy (Al/Cr, close to 1:1). Thus, one site—(0,0,0)—was filled with one Al atom and the other one—(0,0,0.5)—with one Cr atom. Therefore, the symmetry of the structure was reduced to P-3m1. We then performed a geometric optimisation using DFT. Accurate geometry optimisations were ensured using tight criteria for the convergence of both total electronic energy (±10
−6 eV) and residual forces acting on the nuclei (±0.02 eV·Å
−1). The resulting disorder was thus restricted to the 2a position, which was occupied by Al/Cr atoms with 0.5 occupancy. This led to a first model, which was labelled M0, that contained one Cr, four Sc and seven Al atoms in the cell, and exhibited the P-3m1 symmetry (space group 164). Atomic relaxations kept the shape of the cell intact. This led, after relaxation, to the lattice parameters a
calc = 0.537 nm and c
calc = 0.862 nm and atomic coordinates that were in good agreement with the experimental ones. The atomic coordinates of the output structure are detailed in
Table 6. In particular, the computed values of the lattice parameters came from the atomic optimisation based on the DFT. These theoretical values, as obtained from DFT, were in very good agreement with the experimental single-crystal XRD data that is provided in
Table 4 (a = 0.53424(2) and c = 0.86302(3)), since the differences were less than 0.6%.
Other models with atomic compositions closer to the experimental observations (
Table 7) resulted from a protocol that was based on the supercell code [
30] using the cell parameters from the previous relaxation and the occupancies from the experimental analysis (
Table 5). Sufficiently large supercells were required to minimise the size effects, i.e., to reduce the influence of local environments on their own periodic images in all directions. Each run included a symmetry-based search for equivalent structures. The 2 × 2 × 1 supercell showed the lowest anisotropy (side dimension of approx. 8–10 Å in all directions) and contained several atoms (25 Al, 7 Cr and 16 Sc), which was perfectly compatible with the DFT calculations. While the M
111 model (1 × 1 × 1 cell) was fully optimised (cell shape, cell volume, atomic positions), only the atomic positions were relaxed in the M
112, M
211 and M
221 models (1 × 1 × 2, 2 × 1 × 1 and 2 × 2 × 1 supercells). Their lattice parameters were fixed according to the ones of the M
111 model.
Total energy calculations were systematically performed using a variety of configurations within the 1 × 1 × 1, 1 × 1 × 2 and 2 × 1 × 1 supercells, which limited the number of combinations that were achievable with quantum chemical calculations. For the 2 × 2 × 1 supercell, a single configuration was considered (M221) after a random selection from among all possible configurations. It was found to be representative of the grown crystal according to its chemical composition and exhibited a diffraction pattern that was close to the experimental observations. Yet, DFT calculations cannot be achieved with partial or mixed occupancies in a simple way. Our structural models were then built from XRD data but were modified in order to obey the constraints of full occupancy of all sites that were introduced in the computational box. It then modified the composition that was determined using XRD. We believe that this difference was not sufficient to make our conclusions invalid. Note that the DFT computation was done at 0 K, with an accuracy of approx. 1%, which was much smaller than any lattice parameter variation due to temperature.
The total energy calculations were systematically performed using all possible combinations in the case of the 1 × 1 × 1 (1), 1 × 1 × 2 (4) and 2 × 1 × 1 (8) supercells (the number between brackets is the number of calculations performed). According to these calculations, the deviation that was calculated for the formation energies was smaller than 3 meV/atom, i.e., much smaller than the formation energies (between −361 meV/atom and −394 meV/atom), and rather similar within a given cell type. It strongly depended on the cell shape, as demonstrated by the comparison of our results that were calculated using the elongated 1 × 1 × 2 simulation box and the more isotropic 2 × 1 × 1 one. Only one configuration was considered for the 2 × 2 × 1 supercell because our objective was the determination of the formation energy, which was shown to present only tiny variations within a given supercell.
Electronic structure calculations were performed using the M
221 model. Standard DFT calculations highlighted a magnetic compound due to the presence of Cr 3d states, resulting in a calculated total magnetisation of 12.27μ
B in the cell. The magnetic properties of the compound were also indicated by a shift between the observed spin-up and spin-down contributions to the DOS, which is shown in
Figure 9, together with the Al s,p; Cr s,p and d; and Sc s,p and d partial DOSs. We took the non-magnetic Cr crystal as the reference to calculate the formation energies. Obviously, this is not the realistic ground state for bcc chromium [
31,
32]. Indeed, neutron diffraction and coherent X-ray diffraction experiments showed the magnetic ground state of bcc Cr to be a spin-density wave (SDW) with an incommensurate period regarding the crystal lattice below its Néel temperature of 311 K. The SDW corresponded to a quasi-sinusoidal modulation of the magnitude of the magnetic moments along the propagation of the wave, keeping a locally antiferromagnetic order. More precisely, from 0 to 123 K, the SDW was longitudinally polarised with magnetic moments that were oriented along a 100 axis of the crystal lattice, roughly corresponding to a period of 20 lattice parameters. At 123 K, the polarisation of the SDW switched to transverse, with magnetic moments directed perpendicular to its propagation direction, before vanishing at the Néel temperature.
A deeper investigation of the magnetic properties of Al-Cr-Sc would require extensive calculations. Using the M221 model, our spin-polarised calculation ended up with six Cr atoms showing a positive magnetic moment, and one Cr atom that was coupled antiferromagnetically with the others. The mean magnetic moment per Cr atom was calculated by dividing the total magnetic moment of the supercell by the number of Cr atoms (12.27/7 = 1.75 μ
B). The magnetic moment that was carried by Cr atoms was found to be larger than the magnetic moment of bcc chromium, which lies between 0.9 and 1.2 μ
B [
32].
The Bader charge analysis [
32,
33,
34,
35,
36] showed that a charge transfer occurred from the Sc atoms that were positively charged (+1.27 el/at), whereas the Cr and Al atoms exhibited an average charge of −0.82 el/at and −0.59 el/at, respectively. These results were consistent with the respective electronegativities of the Sc, Al and Cr elements, respectively, according to the Pauling scale. The amount of charge transfer was also found to be very similar to the one that was calculated recently for the φ-Al
8Cr
4Sc compound, except for Al (which was positively charged in φ-Al
8Cr
4Sc) [
4].
The total DOS presented a pronounced sp character in the [−10, +4] eV region, which mostly arose from the Al atoms. The Cr and Sc d states showed main contributions above −3 eV, where several maxima were observed. Faint features overlapped along the energy axis in the DOS between the Cr and Sc d states, and the Al sp states, highlighting a non-negligible hybridisation. The metallic character of the compound was assessed from the many states that were present at the Fermi energy (EF). No marked pseudo-gap was found at EF or in its close vicinity, but a shallow pseudo-gap was visible at approx. −0.5 eV under the Fermi energy, which produced a weak but definite contribution to the thermodynamic stability of the compound.