Design and Realization of a Compact Efficient Beam Combiner, Based on Liquid Crystal Pancharatnam–Berry Phase Gratings
Abstract
:1. Introduction
2. Materials and Methods
2.1. Liquid Crystal Sample Preparation
2.2. Photoalignment Patterning and Fabrication
3. Results
3.1. Characterization of the Gratings
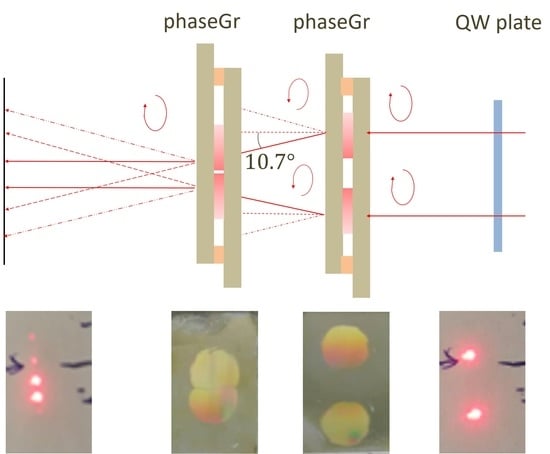
3.2. Characterization of the Beam Combiner
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marrucci, L.; Manzo, C.; Paparo, D. Pancharatnam–Berry phase optical elements for wave front shaping in the visible domain: Switchable helical mode generation. Appl. Phys. Lett. 2006, 88, 221102. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Weng, Y.; Xu, D.; Tabiryan, N.V.; Wu, S.T. Beam steering for virtual/augmented reality displays with a cycloidal diffractive waveplate. Opt. Express 2016, 24, 7287–7298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, M.; Yu, H.; Feng, X.; Guo, Y.; Chaganava, I.; Turiv, T.; Lavrentovich, O.D.; Wei, Q.H. Liquid Crystal Pancharatnam–Berry Micro-Optical Elements for Laser Beam Shaping. Adv. Opt. Mater. 2018, 6, 1800961. [Google Scholar] [CrossRef]
- Slussarenko, S.; Alberucci, A.; Jisha, C.P.; Piccirillo, B.; Santamato, E.; Assanto, G.; Marrucci, L. Guiding light via geometric phases. Nat. Photonics 2016, 10, 571. [Google Scholar] [CrossRef] [Green Version]
- Moon, S.; Lee, C.K.; Nam, S.W.; Jang, C.; Lee, G.Y.; Seo, W.; Sung, G.; Lee, H.S.; Lee, B. Augmented reality near-eye display using Pancharatnam–Berry phase lenses. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.H.; Tan, G.; Zhan, T.; Weng, Y.; Liu, G.; Gou, F.; Peng, F.; Tabiryan, N.V.; Gauza, S.; Wu, S.T. Recent progress in Pancharatnam–Berry phase optical elements and the applications for virtual/augmented realities. Opt. Data Process. Storage 2017, 3, 79–88. [Google Scholar] [CrossRef]
- Kim, J.; Oh, C.; Escuti, M.J.; Serati, S. Wide-angle nonmechanical beam steering using thin liquid crystal polarization gratings. In Advanced Wavefront Control: Methods, Devices, and Applications VI; SPIE: San Diego, CA, USA, 2008; Volume 7093, p. 709302. [Google Scholar]
- Ichimura, K. Photoalignment of liquid-crystal systems. Chem. Rev. 2000, 100, 1847–1874. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Li, Y.; Miskiewicz, M.N.; Oh, C.; Kudenov, M.W.; Escuti, M.J. Fabrication of ideal geometric-phase holograms with arbitrary wavefronts. Optica 2015, 2, 958–964. [Google Scholar] [CrossRef]
- Zhan, T.; Xiong, J.; Lee, Y.H.; Chen, R.; Wu, S.T. Fabrication of Pancharatnam–Berry phase optical elements with highly stable polarization holography. Opt. Express 2019, 27, 2632–2642. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yaroshchuk, O.; Reznikov, Y. Photoalignment of liquid crystals: Basics and current trends. J. Mater. Chem. 2012, 22, 286–300. [Google Scholar] [CrossRef]
- Kim, J.; Oh, C.; Serati, S.; Escuti, M.J. Wide-angle, nonmechanical beam steering with high throughput utilizing polarization gratings. Appl. Opt. 2011, 50, 2636–2639. [Google Scholar] [CrossRef] [PubMed]
- Gou, F.; Peng, F.; Ru, Q.; Lee, Y.H.; Chen, H.; He, Z.; Zhan, T.; Vodopyanov, K.L.; Wu, S.T. Mid-wave infrared beam steering based on high-efficiency liquid crystal diffractive waveplates. Opt. Express 2017, 25, 22404–22410. [Google Scholar] [CrossRef] [PubMed]
- Bhandari, R. Polarization of light and topological phases. Phys. Rep. 1997, 281, 1–64. [Google Scholar] [CrossRef]
- Feugnet, G.; Bussac, C.; Larat, C.; Schwarz, M.; Pocholle, J.P. High-efficiency TEM00 Nd:YVO4 laser longitudinally pumped by a high-power array. Opt. Lett. 1995, 20, 157–159. [Google Scholar] [CrossRef] [PubMed]
- Janssens, P.; Malfait, K. Future prospects of high-end laser projectors. In Proceedings of the Emerging Liquid Crystal Technologies IV, San Jose, CA, USA, 25–28 January 2009; Chien, L.C., Wu, M.H., Eds.; Volume 7232. [Google Scholar] [CrossRef]
- Wang, P.; Gheen, A.; Wang, Z. Beam shaping technology for laser diode arrays. In Proceedings of the 3rd Conference on Laser Beam Shaping, Seattle, WA, USA, 9–11 July 2002; Dickey, F.M., Holswade, S.C., Shealy, D.L., Eds.; Volume 4770, pp. 131–135. [Google Scholar] [CrossRef]
- Bokor, N.; Davidson, N. Adiabatic shaping of diffuse light with a tapered gradient-index element. Opt. Commun. 2001, 196, 9–16. [Google Scholar] [CrossRef]
- Ghasemi, S.H.; Lafouti, M. A beam shaping design for coupling high power diode laser stack to fiber with capability of spectral narrowing and stabilizing. Opt. Commun. 2012, 285, 2879–2882. [Google Scholar] [CrossRef]
- Oh, C.; Escuti, M.J. Numerical analysis of polarization gratings using the finite-difference time-domain method. Phys. Rev. A 2007, 76, 043815. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wen, C.H.; Gauza, S.; Lu, R.; Wu, S.T. Refractive indices of liquid crystals for display applications. J. Display Technol. 2005, 1, 51. [Google Scholar] [CrossRef]
- Escuti, M.J.; Oh, C.; Sánchez, C.; Bastiaansen, C.; Broer, D.J. Simplified spectropolarimetry using reactive mesogen polarization gratings. In Imaging Spectrometry XI. International Society for Optics and Photonics; SPIE: San Diego, CA, USA, 2006; Volume 6302, p. 630207. [Google Scholar]






| Diffraction Order | 2 | 1 | 0 | Total | |
|---|---|---|---|---|---|
| sample1-grating1 | 0.07% | 99.03% | 0.71% | 0.19% | 100% |
| sample1-grating2 | 0.04% | 98.07% | 1.69% | 0.19% | 100% |
| sample2-grating1 | 0.03% | 98.50% | 1.28% | 0.19% | 100% |
| sample2-grating2 | 0.07% | 99.28% | 0.61% | 0.03% | 100% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, B.; Beeckman, J.; Neyts, K. Design and Realization of a Compact Efficient Beam Combiner, Based on Liquid Crystal Pancharatnam–Berry Phase Gratings. Crystals 2021, 11, 220. https://doi.org/10.3390/cryst11020220
Gao B, Beeckman J, Neyts K. Design and Realization of a Compact Efficient Beam Combiner, Based on Liquid Crystal Pancharatnam–Berry Phase Gratings. Crystals. 2021; 11(2):220. https://doi.org/10.3390/cryst11020220
Chicago/Turabian StyleGao, Boxuan, Jeroen Beeckman, and Kristiaan Neyts. 2021. "Design and Realization of a Compact Efficient Beam Combiner, Based on Liquid Crystal Pancharatnam–Berry Phase Gratings" Crystals 11, no. 2: 220. https://doi.org/10.3390/cryst11020220
APA StyleGao, B., Beeckman, J., & Neyts, K. (2021). Design and Realization of a Compact Efficient Beam Combiner, Based on Liquid Crystal Pancharatnam–Berry Phase Gratings. Crystals, 11(2), 220. https://doi.org/10.3390/cryst11020220