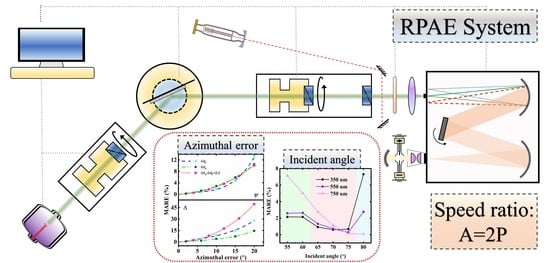
Method for Analyzing the Measurement Error with Respect to Azimuth and Incident Angle for the Rotating Polarizer Analyzer Ellipsometer
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Incident Angle and Principal Angle
3.1.1. Spectroscopic Measurement
3.1.2. Monochromatic Measurement
3.2. Azimuthal Error
3.2.1. Theoretical Analysis
3.2.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Azzam, R.M.A.; Bashara, N.M. Ellipsometry and Polarized Light; North-Holland: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Hauge, P.S. Recent developments in instrumentation in ellipsometry. Surf. Sci. 1980, 96, 108–140. [Google Scholar] [CrossRef]
- Woollam, J.A.; Snyder, P.G.; Rost, M.C. Variable angle spectroscopic ellipsometry—A non-destructive characterization technique for ultrathin and multilayer materials. Thin Solid Film. 1988, 166, 317–323. [Google Scholar] [CrossRef]
- Collins, R.W. Automatic rotating element ellipsometers: Calibration, operation, and real-time applications. Rev. Sci. Instrum. 1990, 61, 2029–2062. [Google Scholar] [CrossRef]
- Aspnes, D.E. Expanding horizons: New developments in ellipsometry and polarimetry. Thin Solid Film. 2004, 455–456, 3–13. [Google Scholar] [CrossRef]
- Tompkins, H.G.; Irene, E.A. Handbook of Ellipsometry; William Andrew: New York, NY, USA, 2005. [Google Scholar]
- Fujiwara, H. Spectroscopic Ellipsometry: Principles and Applications; John Wiley & Sons: Tokyo, Japan, 2007. [Google Scholar]
- Aspnes, D.E. Spectroscopic ellipsometry—Past, present, and future. Thin Solid Film. 2014, 571, 334–344. [Google Scholar] [CrossRef]
- Azzam, R.M.A. Polarization, thin-film optics, ellipsometry, and polarimetry: Retrospective. J. Vac. Sci. Technol. B 2019, 37, 060802. [Google Scholar] [CrossRef]
- Cahan, B.D.; Spanier, R.F. A high speed precision automatic ellipsometer. Surf. Sci. 1969, 16, 166–176. [Google Scholar] [CrossRef]
- Stobie, R.W.; Rao, B.; Dignam, M.J. Analysis of a novel ellipsometric technique with special advantages for infrared spectroscopy. J. Opt. Soc. Am. 1975, 65, 25–28. [Google Scholar] [CrossRef]
- Aspnes, D.E. Fourier transform detection system for rotating-analyzer ellipsometers. Opt. Commun. 1973, 8, 222–225. [Google Scholar] [CrossRef]
- Aspnes, D.E.; Studna, A.A. High Precision Scanning Ellipsometer. Appl. Opt. 1975, 14, 220. [Google Scholar] [CrossRef]
- Schubert, M.; Rheinlander, B.; Woollam, J.A.; Johs, B.; Herzinger, C.M. Extension of rotating-analyzer ellipsometry to generalized ellipsometry: Determination of the dielectric function tensor from uniaxial TiO2. J. Opt. Soc. Am. 1996, 13, 875. [Google Scholar] [CrossRef]
- Azzam, R.M.A. A simple Fourier photopolarimeter with rotating polarizer and analyzer for measuring Jones and Mueller matrices. Opt. Commun. 1978, 25, 137–140. [Google Scholar] [CrossRef]
- Chen, L.Y.; Lynch, D.W. Scanning ellipsometer by rotating polarizer and analyzer. Appl. Opt. 1987, 26, 5221–5228. [Google Scholar] [CrossRef]
- Chen, L.Y.; Feng, X.W.; Su, Y.; Ma, H.Z.; Qian, Y.H. Improved rotating analyzer-polarizer type of scanning ellipsometer. Thin Solid Films 1993, 234, 385–389. [Google Scholar] [CrossRef]
- Chen, L.Y.; Feng, X.W.; Su, Y.; Ma, H.Z.; Qian, Y.H. Design of a scanning ellipsometer by synchronous rotation of the polarizer and analyzer. Appl. Opt. 1994, 33, 1299–1305. [Google Scholar] [CrossRef]
- El-Agez, T.M.; El Tayyan, A.A.; Taya, S.A. Rotating polarizer-analyzer scanning ellipsometer. Thin Solid Film. 2010, 518, 5610–5614. [Google Scholar] [CrossRef]
- El-Agez, T.M.; Taya, S.A. Development and construction of rotating polarizer analyzer ellipsometer. Opt. Laser. Eng. 2011, 49, 507–513. [Google Scholar] [CrossRef]
- Mccrackin, F.L. Analyses and corrections of instrumental errors in ellipsometry. J. Opt. Soc. Am. 1970, 60, 57–63. [Google Scholar] [CrossRef]
- Aspnes, D.E. Measurement and correction of first-order errors in ellipsometry. J. Opt. Soc. Am. 1971, 61, 1077–1085. [Google Scholar] [CrossRef]
- Aspnes, D.E. Optimizing precision of rotating-analyzer ellipsometers. J. Opt. Soc. Am. 1974, 64, 639–646. [Google Scholar] [CrossRef]
- Aspnes, D.E. Optimizing precision of rotating-analyzer and rotating-compensator-ellipsometers. J. Opt. Soc. Am. 2004, 21, 403–410. [Google Scholar] [CrossRef] [PubMed]
- Azzam, R.M.A.; Bashara, N.M. Unified analysis of ellipsometry errors due to imperfect components, cell-window birefringence, and incorrect azimuth angles. J. Opt. Soc. Am. 1971, 61, 600–607. [Google Scholar] [CrossRef]
- Azzam, R.M.A.; Bashara, N.M. Analysis of systematic errors in rotating-analyzer ellipsometers. J. Opt. Soc. Am. 1974, 64, 1459–1469. [Google Scholar] [CrossRef]
- Zeidler, J.R.; Kohles, R.B.; Bashara, N.M. Beam Deviation Errors in Ellipsometric Measurements; an Analysis. Appl. Opt. 1974, 13, 1938–1945. [Google Scholar] [CrossRef] [Green Version]
- Jin, L.; Kasuga, S.; Kondoh, E. General window correction method for ellipsometry measurements. Opt. Express 2014, 22, 27811–27820. [Google Scholar] [CrossRef]
- Nissim, N.; Eliezer, S.; Bakshi, L.; Moreno, D.; Perelmutter, L. In situ correction of windows’ linear birefringence in ellipsometry measurements. Opt. Commun. 2009, 282, 3414–3420. [Google Scholar] [CrossRef]
- Humlicek, J. Sensitivity extrema in multiple-angle ellipsometry. J. Opt. Soc. Am. A 1985, 2, 713–722.31. [Google Scholar] [CrossRef]
- Kleim, R.; Kuntzler, L.; El Ghemmaz, A. Systematic errors in rotating-compensator ellipsometry. J. Opt. Soc. Am. A 1994, 11, 2550–2559. [Google Scholar] [CrossRef]
- Bertucci, S.; Pawlowski, A.; Nicolas, N.; Johann, L.; El Ghemmaz, A.; Stein, N.; Kleim, R. Systematic errors in fixed polarizer, rotating polarizer, sample, fixed analyzer spectroscopic ellipsometry. Thin Solid Films 1998, 313–314, 73–78. [Google Scholar] [CrossRef]
- Chao, Y.F.; Lee, K.Y.; Lin, Y.D. Analytical solutions of the azimuthal deviation of a polarizer and an analyzer by polarizer-sample-analyzer ellipsometry. Appl. Opt. 2006, 45, 3935–3939. [Google Scholar] [CrossRef]
- Nijs, J.M.M.; Silfhout, A.V. Systematic and random errors in rotating-analyzer, ellipsometry. J. Opt. Soc. Am. A 1988, 5, 773–781. [Google Scholar] [CrossRef]
- En Naciri, A.; Broch, L.; Johann, L.; Kleim, R. Fixed polarizer, rotating-polarizer and fixed analyzer spectroscopic ellipsometer: Accurate calibration method, effect of errors and testing. Thin Solid Films 2002, 406, 103–112. [Google Scholar] [CrossRef]
- Nguyen, N.V.; Pudliner, B.S.; An, I.; Collins, R.W. Error correction for calibration and data reduction in rotating-polarizer ellipsometry applications to a novel multichannel ellipsometer. J. Opt. Soc. Am. A 1991, 8, 919–931. [Google Scholar] [CrossRef]
- Nee, S. Error analysis for Mueller matrix measurement. J. Opt. Soc. Am. A 2003, 20, 1651–1657. [Google Scholar] [CrossRef]
- Broch, L.; Naciri, A.E.; Johann, L. Systematic errors for a Mueller matrix dual rotating compensator ellipsometer. Opt. Express 2008, 16, 8814–8824. [Google Scholar] [CrossRef] [PubMed]
- El-Agez, T.M.; Taya, S.A. An extensive theoretical analysis of the 1:2 ratio rotating polarizer–analyzer Fourier ellipsometer. Phys. Scr. 2011, 83, 25701. [Google Scholar] [CrossRef]
- Mao, P.; Zheng, Y.; Cai, Q.; Zhang, D.; Zhang, R.; Zhao, H.; Chen, L. Approach to Error Analysis and Reduction for Rotating-Polarizer-Analyzer Ellipsometer. J. Phys. Soc. Jpn. 2012, 81, 124003. [Google Scholar] [CrossRef]
- Hajduk, B.; Bednarski, H.; Trzebicka, B. Temperature-Dependent Spectroscopic Ellipsometry of Thin Polymer Films. J. Phys. Chem. B 2020, 124, 3229–3251. [Google Scholar] [CrossRef] [PubMed]
- Nosidlak, N.; Jaglarz, J.; Danel, A. Ellipsometric studies for thin polymer layers of organic photovoltaic cells. J. Vac. Sci. Technol. B 2019, 37, 062402. [Google Scholar] [CrossRef]
- Hajduk, B.; Bednarski, H.; Jarząbek, B.; Nitschke, P.; Janeczek, H. Phase diagram of P3HT:PC70BM thin films based on variable-temperature spectroscopic ellipsometry. Polym. Test 2020, 84, 106383. [Google Scholar] [CrossRef]
- Jarząbek, B.; Nitschke, P.; Hajduk, B.; Domański, M.; Bednarski, H. In situ thermo-optical studies of polymer:fullerene blend films. Polym. Test 2020, 88, 106573. [Google Scholar] [CrossRef]
- Azzam, R.M.A. Contours of constant principal angle and constant principal azimuth in the complex epsilon-plane. J. Opt. Soc. Am. A 1981, 71, 1523–1528. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Zhao, H.; Zhang, R.; Ma, Y.; Liu, Z.; Li, J.; Shen, Z.; Wang, S.; Chen, L. Analytical study of the principal angle used in optical experiments. Appl. Opt. 2002, 41, 2592–2595. [Google Scholar] [CrossRef] [PubMed]
- Aspnes, D.E.; Kinsbron, E.; Bacon, D.D. Optical-properties of Au: Sample effects. Phys. Rev. B 1980, 21, 3290–3299. [Google Scholar] [CrossRef]
- Takeuchi, K.; Adachi, S. Optical properties of β-Sn films. J. Appl. Phys. 2009, 105, 073520. [Google Scholar] [CrossRef]









| Incident Angle (°) | 55 | 60 | 65 | 70 | 75 | 80 |
|---|---|---|---|---|---|---|
| MARE-ε1 (%) | 6.25 | 4.90 | 1.78 | 0.10 | 1.70 | 1.94 |
| MARE-ε2 (%) | 9.12 | 5.45 | 3.8 | 1.39 | 4.19 | 4.19 |
| Incident Angle (°) | 55 | 60 | 65 | 70 | 75 | 80 |
|---|---|---|---|---|---|---|
| Amount of data points | 30 | 27 | 96 | 100 | 68 | 8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, H.; Zheng, Y.; Shan, Y.; Chen, Y.; Zhang, H.; Zhang, R.; Wang, S.; Li, J.; Lee, Y.; Chen, L. Method for Analyzing the Measurement Error with Respect to Azimuth and Incident Angle for the Rotating Polarizer Analyzer Ellipsometer. Crystals 2021, 11, 349. https://doi.org/10.3390/cryst11040349
Tu H, Zheng Y, Shan Y, Chen Y, Zhang H, Zhang R, Wang S, Li J, Lee Y, Chen L. Method for Analyzing the Measurement Error with Respect to Azimuth and Incident Angle for the Rotating Polarizer Analyzer Ellipsometer. Crystals. 2021; 11(4):349. https://doi.org/10.3390/cryst11040349
Chicago/Turabian StyleTu, Huatian, Yuxiang Zheng, Yao Shan, Yao Chen, Haotian Zhang, Rongjun Zhang, Songyou Wang, Jing Li, YoungPak Lee, and Liangyao Chen. 2021. "Method for Analyzing the Measurement Error with Respect to Azimuth and Incident Angle for the Rotating Polarizer Analyzer Ellipsometer" Crystals 11, no. 4: 349. https://doi.org/10.3390/cryst11040349
APA StyleTu, H., Zheng, Y., Shan, Y., Chen, Y., Zhang, H., Zhang, R., Wang, S., Li, J., Lee, Y., & Chen, L. (2021). Method for Analyzing the Measurement Error with Respect to Azimuth and Incident Angle for the Rotating Polarizer Analyzer Ellipsometer. Crystals, 11(4), 349. https://doi.org/10.3390/cryst11040349