Design, Simulation, and Analysis of Optical Microring Resonators in Lithium Tantalate on Insulator
Abstract
:1. Introduction
2. Device Description
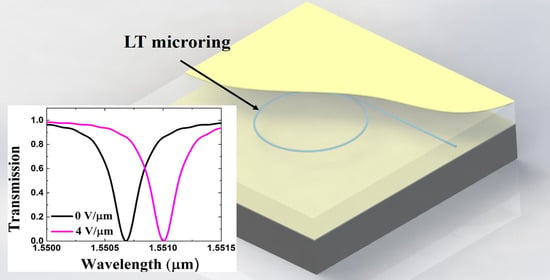
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bogaerts, W.; De Heyn, P.; Van Vaerenbergh, T.; De Vos, K.; Selvaraja, S.K.; Claes, T.; Dumon, P.; Bienstman, P.; Van Thourhout, D.; Baets, R. Silicon microring resonators. Laser Photonics Rev. 2012, 6, 47–73. [Google Scholar] [CrossRef]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Xiang, B. Simulation and analysis of electro-optic tunable microring resonators in silicon thin film on lithium niobate. Sic. Rep. 2019, 9, 6302. [Google Scholar] [CrossRef] [PubMed]
- Mak, J.C.C.; Sacher, W.D.; Xue, T.Y.; Mikkelsen, J.C.; Yong, Z.; Poon, J.K.S. Automatic resonance alignment of high-order microring filters. IEEE J. Quantum. Elect. 2015, 51, 1–11. [Google Scholar] [CrossRef]
- Barwicz, T.; Popovic, M.A.; Rakich, P.T.; Watts, M.R.; Haus, H.A.; Ippen, E.P.; Smith, H.I. Microring-resonator-based add-drop filters in SiN: Fabrication and analysis. Opt. Express 2004, 12, 1437–1442. [Google Scholar] [CrossRef]
- Chen, G.P.; Jiang, C. Reverse design of microring resonator channel dropping filters. Results Phys. 2020, 19, 103380. [Google Scholar] [CrossRef]
- Xu, Q.F.; Manipatruni, S.; Schmidt, B.; Shakya, J.; Lipson, M. 12.5 Gbit/s carrier-injection-based silicon micro-ring silicon modulators. Opt. Express 2007, 15, 430–436. [Google Scholar] [CrossRef] [Green Version]
- Cao, W.; Hagan, D.; Thomson, D.J.; Nedeljkovic, M.; Littlejohns, C.G.; Knights, A.; Alam, S.U.; Wang, J.J.; Gardes, F.; Zhang, W.W.; et al. High-speed silicon modulators for the 2 μm wavelength band. Optica 2018, 5, 1055–1062. [Google Scholar] [CrossRef]
- Wang, Y.H.; Lv, P.; Zhang, Y.L.; Song, M.X.; Liu, C.L.; Wang, G.F.; Wang, C.X.; Qin, Z.K. Analysis of characteristics of a parallel channel microring resonator electro-optic switch array. Optik 2018, 165, 332–340. [Google Scholar] [CrossRef]
- Emelett, S.J.; Soref, R. Design and simulation of silicon microring optical routing switches. J. Lightwave Technol. 2005, 23, 1800–1807. [Google Scholar] [CrossRef]
- Cardenas, J.; Foster, M.A.; Sherwood-Droz, N.; Poitras, C.B.; Lira, H.L.R.; Zhang, B.B.; Gaeta, A.L.; Khurgin, J.B.; Morton, P.; Lipson, M. Wide-bandwidth continuously tunable optical delay line using silicon microring resonators. Opt. Express 2010, 18, 26525–26534. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, M.; Buscaino, B.; Wang, C.; Shams-Ansari, A.; Reimer, C.; Zhu, R.R.; Kahn, J.M.; Loncar, M. Broadband electro-optic frequency comb generation in a lithium niobate microring resonator. Nature 2019, 568, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Kovach, A.; Chen, D.Y.; He, J.H.; Choi, H.; Dogan, A.H.; Ghasemkhani, M.; Taheri, H.; Armani, A.M. Emerging material systems for integrated optical Kerr frequency combs. Adv. Opt. Photonics 2020, 12, 135–222. [Google Scholar] [CrossRef] [Green Version]
- Fujii, S.; Tanabe, T. Dispersion engineering and measurement of whispering gallery mode microresonator for Kerr frequency comb generation. Nanophotonics 2020, 9, 1087–1104. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Zhang, M.; Yu, M.J.; Zhu, R.R.; Hu, H.; Loncar, M. Monolithic lithium niobate photonic circuits for Kerr frequency comb generation and modulation. Nat. Commun. 2019, 10, 978. [Google Scholar] [CrossRef]
- Reed, G.T.; Mashanovich, G.; Gardes, F.Y.; Thomson, D.J. Silicon optical modulators. Nat. Photonics 2010, 4, 518–526. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.F.; Fattal, D.; Beausoleil, R.G. Silicon microring resonators with 1.5-µm radius. Opt. Express 2008, 16, 4309–4315. [Google Scholar] [CrossRef] [Green Version]
- Mi, G.C.; Horvath, C.; Aktary, M.; Van, V. Silicon microring refractometric sensor for atmospheric CO2 gas monitoring. Opt. Express 2016, 24, 1773–1780. [Google Scholar] [CrossRef] [PubMed]
- Zamora, V.; Lutzow, P.; Weiland, M.; Pergande, D. Investigation of cascaded SiN microring resonators at 1.3 µm and 1.5 µm. Opt. Express 2013, 21, 27550–27557. [Google Scholar] [CrossRef]
- Guarino, A.; Poberaj, G.; Rezzonico, D.; Degl’Innocenti, R.; Gunter, P. Electro-optically tunable microring resonators in lithium niobate. Nat. Photonics 2007, 1, 407–410. [Google Scholar] [CrossRef]
- Lu, J.J.; Surya, J.B.; Liu, X.W.; Bruch, A.W.; Gong, Z.; Xu, Y.T.; Tang, H.X. Periodically poled thin-film lithium niobate microring resonators with a second-harmonic generation efficiency of 250,000%/W. Optica 2019, 6, 1455–1460. [Google Scholar] [CrossRef] [Green Version]
- Yu, M.J.; Okawachi, Y.; Cheng, R.; Wang, C.; Zhang, M.; Gaeta, A.L.; Loncar, M. Raman lasing and soliton mode-locking in lithium niobate microresonators. Light. Sci. Appl. 2020, 9, 9. [Google Scholar] [CrossRef] [Green Version]
- Han, H.P.; Xiang, B.X.; Zhang, J.L. Simulation and analysis of single-mode microring resonators in lithium niobate thin films. Crystals 2018, 8, 342. [Google Scholar] [CrossRef] [Green Version]
- Casson, J.L.; Gahagan, K.T.; Scrymgeour, D.A.; Jain, R.K.; Robinson, J.M.; Gopalan, V.; Sander, R.K. Electro-optic coefficients of lithium tantalate at near-infrared wavelengths. J. Opt. Soc. Am. B 2004, 21, 1948–1952. [Google Scholar] [CrossRef] [Green Version]
- Barie, N.; Wessa, T.; Bruns, M.; Rapp, M. Love waves in SiO2 layers on STW-resonators based on LiTaO3. Talanta 2004, 62, 71–79. [Google Scholar] [CrossRef]
- Lobino, M.; Marshall, G.D.; Xiong, C.; Clark, A.S.; Bonneau, D.; Natarajan, C.M.; Tanner, M.G.; Hadfield, R.H.; Dorenbos, S.N.; Zijlstra, T.; et al. Correlated photon-pair generation in a periodically poled MgO doped stoichiometric lithium tantalate reverse proton exchanged waveguide. Appl. Phys. Lett. 2011, 99, 081110. [Google Scholar] [CrossRef] [Green Version]
- Kawachi, O.; Mineyoshi, S.; Endoh, G.; Ueda, M.; Ikata, O.; Hashimoto, K.; Yamaguchi, M. Optimal cut for leaky SAW on LiTaO3 for high performance resonators and filters. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2001, 48, 1442–1448. [Google Scholar] [CrossRef] [PubMed]
- Takai, T.; Iwamoto, H.; Takamine, Y.; Yamazaki, H.; Fuyutsume, T.; Kyoya, H.; Nakao, T.; Kando, H.; Hiramoto, M.; Toi, T.; et al. High performance SAW resonator on new mutilayered substrate using LiTaO3 crystal. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 1382–1389. [Google Scholar] [CrossRef]
- Yan, X.S.; Liu, Y.A.; Ge, L.C.; Zhu, B.; Wu, J.W.; Chen, Y.P.; Chen, X.F. High optical damage threshold on-chip lithium tantalate microdisk resonator. Opt. Lett. 2020, 45, 4100–4103. [Google Scholar] [CrossRef]
- Yan, Y.Q.; Huang, K.; Zhou, H.Y.; Zhao, X.M.; Li, W.Q.; Li, Z.X.; Yi, A.L.; Huang, H.; Lin, J.J.; Zhang, S.B.; et al. Wafer-scale fabrication of 42° rotated Y-cut LiTaO3-on-insulator (LTOI) substrate for a SAW resonator. ACS Appl. Electron. Mater. 2019, 1, 1660–1666. [Google Scholar] [CrossRef]
- Tauzin, A.; Dechamp, J.; Madeira, F.; Mazen, F.; Zussy, M.; Deguet, C.; Clavelier, L.; Moulet, J.S.; Richtarch, C.; Akatsu, T.; et al. 3-inch single-crystal LiTaO3 films onto metallic electrode using Smart CutTM technology. Electron. Lett. 2008, 44, 822–824. [Google Scholar] [CrossRef]
- Ma, C.D.; Lu, F.; Xu, B.; Fan, R.R. Visualized strain profile in the process of crystal ion slicing of LiTaO3. J. Phys. D Appl. Phys. 2016, 49, 205301. [Google Scholar] [CrossRef]
- Berenger, J.P. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Smith, R.T.; Welsh, F.S. Temperature dependence of the elastic, piezoelectric, and dielectric constants of lithium tantalate and lithium niobate. J. Appl. Phys. 1971, 42, 2219–2230. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, M.; Stern, B.; Lipson, M.; Lončar, M. Nanophotonic lithium niobate electro-optic modulators. Opt. Express 2018, 26, 1547–1555. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mahmoud, M.; Cai, L.; Bottenfield, C.; Piazza, G. Lithium niobate electro-optic racetrack modulator etched in Y-cut LNOI platform. IEEE Photonics J. 2018, 10, 6600410. [Google Scholar] [CrossRef]
- Chen, L.; Xu, Q.; Wood, M.G.; Reano, R.M. Hybrid silicon and lithium niobate electro-optical ring modulator. Optica 2014, 1, 112–118. [Google Scholar] [CrossRef]
- Chen, L.; Chen, J.; Nagy, J.; Reano, R.M. Highly linear ring modulator from hybrid silicon and lithium niobate. Opt. Express 2015, 23, 13255–13264. [Google Scholar] [CrossRef] [PubMed]
- Krasnokutska, I.; Tambasco, J.L.J.; Peruzzo, A. Tunable large free spectral range microring resonators in lithium niobate on insulator. Sci. Rep. 2019, 9, 11086. [Google Scholar] [CrossRef] [Green Version]
- Siew, S.Y.; Saha, S.S.; Tsang, M.; Danner, A.J. Rib Microring Resonators in Lithium Niobate on Insulator. IEEE Photonics Technol. Lett. 2016, 28, 573–576. [Google Scholar] [CrossRef]









| Material | LiTaO3 | SiO2 | Si |
|---|---|---|---|
| Refractive index | no = 2.1189 ne = 2.1228 | 1.46 | 3.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, S.; Han, H.; Jiang, S.; Xiang, B.; Chai, G.; Ruan, S. Design, Simulation, and Analysis of Optical Microring Resonators in Lithium Tantalate on Insulator. Crystals 2021, 11, 480. https://doi.org/10.3390/cryst11050480
Yao S, Han H, Jiang S, Xiang B, Chai G, Ruan S. Design, Simulation, and Analysis of Optical Microring Resonators in Lithium Tantalate on Insulator. Crystals. 2021; 11(5):480. https://doi.org/10.3390/cryst11050480
Chicago/Turabian StyleYao, Siyang, Huangpu Han, Shangen Jiang, Bingxi Xiang, Guangyue Chai, and Shuangchen Ruan. 2021. "Design, Simulation, and Analysis of Optical Microring Resonators in Lithium Tantalate on Insulator" Crystals 11, no. 5: 480. https://doi.org/10.3390/cryst11050480
APA StyleYao, S., Han, H., Jiang, S., Xiang, B., Chai, G., & Ruan, S. (2021). Design, Simulation, and Analysis of Optical Microring Resonators in Lithium Tantalate on Insulator. Crystals, 11(5), 480. https://doi.org/10.3390/cryst11050480