Absence of Superconductivity in the Hubbard Dimer Model for κ-(BEDT-TTF)2X
Abstract
:1. Introduction
2. Methods
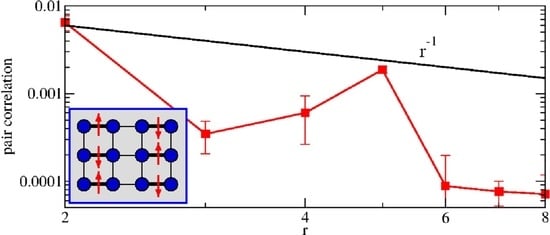
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statements
Conflicts of Interest
References
- Mazumdar, S. A unified theoretical approach to superconductors with strong Coulomb correlations: The organics, LiTi2O4, electron- and hole-doped copper oxides and doped BaBiO3. In Interacting Electrons in Reduced Dimensions. Proceedings of a NATO Advanced Research Workshop; Baeriswyl, D., Campbell, D.K., Eds.; Plenum: New York, NY, USA, 1989; pp. 315–329.BaBiO3. In Interacting Electrons in Reduced Dimensions. Proceedings of a NATO Advanced Research Workshop; Baeriswyl, D., Campbell, D.K., Baeriswyl, D., Campbell, D.K., Eds.; Plenum: New York, NY, USA, 1989; pp. 315–329. [Google Scholar]
- Uemura, Y.J.; Le, L.P.; Luke, G.M.; Sternlieb, B.J.; Wu, W.D.; Brewer, J.H.; Riseman, T.M.; Seaman, C.L.; Maple, M.B.; Ishikawa, M.; et al. Basic similarities among cuprate, bismuthate, organic, Chevrel-phase, and heavy-fermion superconductors shown by penetration-depth measurements. Phys. Rev. Lett. 1991, 66, 2665–2668. [Google Scholar] [CrossRef]
- Fukuyama, H.; Hasegawa, Y. Superconductivity in organics and oxides: Similarity and dissimilarity. Physica B+C 1987, 148, 204–211. [Google Scholar] [CrossRef]
- Fukuyama, H. On some organic conductors in the light of oxide superconductors. In Physics and Chemistry of Organic Superconductors. Proceedings of the ISSP International Symposium; Saito, G., Kagoshima, S., Eds.; Springer: Berlin, Germany, 1990; pp. 15–20. [Google Scholar]
- McKenzie, R.H. Similarities between organic and cuprate superconductors. Science 1997, 278, 820–821. [Google Scholar] [CrossRef] [Green Version]
- Iwasa, Y.; Takenobu, T. Superconductivity, Mott-Hubbard states, and molecular orbital order in intercalated fullerides. J. Phys. Condens. Matter 2003, 15, R495. [Google Scholar] [CrossRef]
- Capone, M.; Fabrizio, M.; Castellani, C.; Tosatti, E. Colloquium: Modeling the unconventional superconducting properties of expanded A3C60 fullerides. Rev. Mod. Phys. 2009, 81, 943–958. [Google Scholar] [CrossRef]
- Mazumdar, S.; Clay, R.T. Is there a common theme behind the correlated-electron superconductivity in organic charge-transfer solids, cobaltates, spinels and fullerides? Phys. Stat. Solidi 2012, 249, 995–998. [Google Scholar] [CrossRef] [Green Version]
- Baskaran, G. RVB states in doped band insulators from Coulomb forces: Theory and a case study of superconductivity in BiS2 layers. Supercond. Sci. Technol. 2016, 29, 124002. [Google Scholar] [CrossRef]
- Jérome, D.; Mazaud, A.; Ribault, M.; Bechgaard, K. Superconductivity in a synthetic organic conductor (TMTSF)2PF6. J. Phys. (Paris) Lett. 1980, 41, L95–L98. [Google Scholar] [CrossRef] [Green Version]
- Kanoda, K.; Kato, R. Mott physics in organic conductors with triangular lattices. Annu. Rev. Condens. Matter Phys. 2011, 2, 167–188. [Google Scholar] [CrossRef]
- Kato, R. Special issue: Molecular conductors. Crystals 2012, 2012, 56–1482. [Google Scholar]
- Brown, S.E. Organic superconductors: The Bechgaard salts and relatives. Physica C 2015, 514, 279–289. [Google Scholar] [CrossRef]
- Clay, R.T.; Mazumdar, S. From charge- and spin-ordering to superconductivity in the organic charge-transfer solids. Phys. Rep. 2019, 788, 1–89. [Google Scholar] [CrossRef] [Green Version]
- Dressel, M.; Tomić, S. Molecular quantum materials: Electronic phases and charge dynamics in two-dimensional organic solids. Adv. Phys. 2020, 69, 1–120. [Google Scholar] [CrossRef]
- Kino, H.; Kontani, H. Phase diagram of superconductivity on the anisotropic triangular lattice Hubbard model: An effective model of κ-(BEDT-TTF) salts. J. Phys. Soc. Jpn. 1998, 67, 3691–3694. [Google Scholar] [CrossRef] [Green Version]
- Schmalian, J. Pairing due to spin fluctuations in layered organic superconductors. Phys. Rev. Lett. 1998, 81, 4232–4235. [Google Scholar] [CrossRef] [Green Version]
- Kondo, H.; Moriya, T. Spin Fluctuation-Induced Superconductivity in Organic Compounds. J. Phys. Soc. Jpn. 1998, 67, 3695–3698. [Google Scholar] [CrossRef] [Green Version]
- Vojta, M.; Dagotto, E. Indications of unconventional superconductivity in doped and undoped triangular antiferromagnets. Phys. Rev. B 1999, 59, R713–R716. [Google Scholar] [CrossRef] [Green Version]
- Baskaran, G. Mott Insulator to High Tc Superconductor via Pressure: Resonating Valence Bond Theory and Prediction of New Systems. Phys. Rev. Lett. 2003, 90, 197007. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Schmalian, J.; Trivedi, N. Pairing and Superconductivity Driven by Strong Quasiparticle Renormalization in Two-Dimensional Organic Charge Transfer Salts. Phys. Rev. Lett. 2005, 94, 127003. [Google Scholar] [CrossRef] [Green Version]
- Kyung, B.; Tremblay, A.M.S. Mott transition, antiferromagnetism, and d-wave superconductivity in two-dimensional organic conductors. Phys. Rev. Lett. 2006, 97, 046402. [Google Scholar] [CrossRef] [Green Version]
- Yokoyama, H.; Ogata, M.; Tanaka, Y. Mott Transitions and d-Wave Superconductivity in Half-Filled-Band Hubbard Model on Square Lattice with Geometric Frustration. J. Phys. Soc. Jpn. 2006, 75, 114706. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, T.; Yokoyama, H.; Tanaka, Y.; Inoue, J. Superconductivity and a Mott Transition in a Hubbard Model on an Anisotropic Triangular Lattice. J. Phys. Soc. Jpn. 2006, 75, 074707. [Google Scholar] [CrossRef] [Green Version]
- Sahebsara, P.; Sénéchal, D. Antiferromagnetism and Superconductivity in Layered Organic Conductors: Variational Cluster Approach. Phys. Rev. Lett. 2006, 97, 257004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nevidomskyy, A.H.; Scheiber, C.; Sénéchal, D.; Tremblay, A.M.S. Magnetism and d-wave superconductivity on the half-filled square lattice with frustration. Phys. Rev. B 2008, 77, 064427. [Google Scholar] [CrossRef] [Green Version]
- Sentef, M.; Werner, P.; Gull, E.; Kampf, A.P. Superconducting Phase and Pairing Fluctuations in the Half-Filled Two-Dimensional Hubbard Model. Phys. Rev. Lett. 2011, 107, 126401. [Google Scholar] [CrossRef] [Green Version]
- Hebert, C.D.; Semon, P.; Tremblay, A.M.S. Superconducting dome in doped quasi-two-dimensional organic Mott insulators: A paradigm for strongly correlated superconductivity. Phys. Rev. B 2015, 92, 195112. [Google Scholar] [CrossRef] [Green Version]
- Clay, R.T.; Li, H.; Mazumdar, S. Absence of superconductivity in the half-filled band Hubbard model on the anisotropic triangular lattice. Phys. Rev. Lett. 2008, 101, 166403. [Google Scholar] [CrossRef]
- Dayal, S.; Clay, R.T.; Mazumdar, S. Absence of long-range superconducting correlations in the frustrated -filled band Hubbard model. Phys. Rev. B 2012, 85, 165141. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, T.; Yokoyama, H.; Tanaka, Y.; Inoue, J. Predominant magnetic states in the Hubbard model on anisotropic triangular lattices. Phys. Rev. B 2008, 77, 214505. [Google Scholar] [CrossRef]
- Tocchio, L.F.; Parola, A.; Gros, C.; Becca, F. Spin-liquid and magnetic phases in the anisotropic triangular lattice: The case of κ-(ET)2X. Phys. Rev. B 2009, 80, 064419. [Google Scholar] [CrossRef] [Green Version]
- Gomes, N.; Clay, R.T.; Mazumdar, S. Absence of superconductivity and valence bond order in the Hubbard-Heisenberg model for organic charge-transfer solids. J. Phys. Condens. Matter 2013, 25, 385603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qin, M.; Chung, C.M.; Shi, H.; Vitali, E.; Hubig, C.; Schollwöck, U.; White, S.R.; Zhang, S. Absence of superconductivity in the pure two-dimensional Hubbard model. Phys. Rev. X 2020, 10, 031016. [Google Scholar] [CrossRef]
- White, S.R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863–2866. [Google Scholar] [CrossRef]
- Fishman, M.; White, S.R.; Stoudenmire, E.M. The ITensor Software Library for Tensor Network Calculations. arXiv 2020, arXiv:2007.14822. [Google Scholar]
- Stoudenmire, E.M.; White, S.R. Real-space parallel density matrix renormalization group. Phys. Rev. B 2013, 87, 155137. [Google Scholar] [CrossRef] [Green Version]
- Chung, C.M.; Qin, M.; Zhang, S.; Schollwöck, U.; White, S.R. Plaquette versus ordinary d-wave pairing in the t′-Hubbard model on a width 4 cylinder. Phys. Rev. B 2020, 102, 041106. [Google Scholar] [CrossRef]
- Luther, A.; Emery, V.J. Backward Scattering in the One-Dimensional Electron Gas. Phys. Rev. Lett. 1974, 33, 589–592. [Google Scholar] [CrossRef]
- Aimi, T.; Imada, M. Does Simple Two-Dimensional Hubbard Model Account for High-Tc Superconductivity in Copper Oxides? J. Phys. Soc. Jpn. 2007, 76, 113708. [Google Scholar] [CrossRef] [Green Version]
- Gomes, N.; De Silva, W.W.; Dutta, T.; Clay, R.T.; Mazumdar, S. Coulomb Enhanced Superconducting Pair Correlations in the Frustrated Quarter-Filled Band. Phys. Rev. B 2016, 93, 165110. [Google Scholar] [CrossRef] [Green Version]
- Clay, R.T.; Gomes, N.; Mazumdar, S. Theory of triangular lattice quasi-one-dimensional charge-transfer-solids. Phys. Rev. B 2019, 100, 115158. [Google Scholar] [CrossRef] [Green Version]
- Dolfi, M.; Bauer, B.; Keller, S.; Troyer, M. Pair correlations in doped Hubbard ladders. Phys. Rev. B 2015, 92, 195139. [Google Scholar] [CrossRef] [Green Version]
- Ito, H.; Asai, T.; Shimizu, Y.; Hayama, H.; Yoshida, Y.; Saito, G. Pressure-induced superconductivity in the antiferromagnet κ-(ET)2CF2(SO)3. Phys. Rev. B 2016, 94, 020503(R). [Google Scholar] [CrossRef]
- Kobayashi, T.; Ding, Q.P.; Taniguchi, H.; Satoh, K.; Kawamoto, A.; Furukawa, Y. Charge disproportionation in the spin-liquid candidate κ-(ET)2Cu2(CN)3 at 6 K revealed by 63Cu NQR measurements. Phys. Rev. Res. 2020, 2, 042023(R). [Google Scholar] [CrossRef]
- Sedlmeier, K.; Elsässer, S.; Neubauer, D.; Beyer, R.; Wu, D.; Ivek, T.; Tomic, S.; Schlueter, J.A.; Dressel, M. Absence of charge order in the dimerized κ-phase BEDT-TTF salts. Phys. Rev. B 2012, 86, 245103. [Google Scholar] [CrossRef] [Green Version]
- Drichko, N.; Beyer, R.; Rose, E.; Dressel, M.; Schlueter, J.A.; Turunova, S.A.; Zhilyaeva, E.I.; Lyubovskaya, R.N. Metallic state and charge-order metal-insulator transition in the quasi-two-dimensional conductor κ-(BEDT-TTF)2Hg(SCN)2Cl. Phys. Rev. B 2014, 89, 075133. [Google Scholar] [CrossRef]
- Hassan, N.M.; Thirunavukkuarasu, K.; Lu, Z.; Smirnov, D.; Zhilyaeva, E.I.; Torunova, S.; Lyubovskaya, R.N.; Drichko, N. Melting of charge order in the low-temperature state of an electronic ferroelectric-like system. NPJ Quant. Mater. 2020, 5, 15. [Google Scholar] [CrossRef]
- Gati, E.; Fischer, J.K.; Lunkenheimer, P.; Zielke, D.; Köhler, S.; Kolb, F.; von Nidda, H.A.K.; Winter, S.M.; Schubert, H.; Schlueter, J.A.; et al. Evidence for Electronically Driven Ferroelectricity in a Strongly Correlated Dimerized BEDT-TTF Molecular Conductor. Phys. Rev. Lett. 2018, 120, 247601. [Google Scholar] [CrossRef] [Green Version]
- Hassan, N.; Cunningham, S.; Mourigal, M.; Zhilyaeva, E.I.; Torunova, S.A.; Lyubovskaya, R.N.; Schlueter, J.A.; Drichko, N. Evidence for a quantum dipole liquid state in an organic quasi–two-dimensional material. Science 2018, 360, 1101–1104. [Google Scholar] [CrossRef] [Green Version]
- Hotta, C. Quantum electric dipoles in spin-liquid dimer Mott insulator κ-(ET)2Cu2(CN)3. Phys. Rev. B 2010, 82, 241104(R). [Google Scholar] [CrossRef] [Green Version]
- Naka, M.; Ishihara, S. Electronic Ferroelectricity in a Dimer Mott Insulator. J. Phys. Soc. Jpn. 2010, 79, 063707. [Google Scholar] [CrossRef]
- Li, H.; Clay, R.T.; Mazumdar, S. The paired-electron crystal in the two-dimensional frustrated quarter-filled band. J. Phys. Condens. Matter 2010, 22, 272201. [Google Scholar] [CrossRef] [PubMed]
- Dayal, S.; Clay, R.T.; Li, H.; Mazumdar, S. Paired electron crystal: Order from frustration in the quarter-filled band. Phys. Rev. B 2011, 83, 245106. [Google Scholar] [CrossRef] [Green Version]
- Seo, H. Charge Ordering in Organic ET Compounds. J. Phys. Soc. Jpn. 2000, 69, 805–820. [Google Scholar] [CrossRef] [Green Version]
- Kaneko, R.; Tocchio, L.F.; Valentí, R.; Becca, F. Charge orders in organic charge-transfer salts. New J. Phys. 2017, 19, 103033. [Google Scholar] [CrossRef] [Green Version]
- De Silva, W.W.; Gomes, N.; Mazumdar, S.; Clay, R.T. Coulomb enhancement of superconducting pair-pair correlations in a -filled model for κ-(BEDT-TTF)2X. Phys. Rev. B 2016, 93, 205111. [Google Scholar] [CrossRef] [Green Version]
- Venderley, J.; Kim, E.A. Density matrix renormalization group study of superconductivity in the triangular lattice Hubbard model. Phys. Rev. B 2019, 100, 060506. [Google Scholar] [CrossRef] [Green Version]
- Clay, R.T.; Roy, D. Superconductivity due to cooperation of electron-electron and electron-phonon interactions at quarter-filling. Phys. Rev. Res. 2020, 2, 023006. [Google Scholar] [CrossRef] [Green Version]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, D.; Clay, R.T.; Mazumdar, S. Absence of Superconductivity in the Hubbard Dimer Model for κ-(BEDT-TTF)2X. Crystals 2021, 11, 580. https://doi.org/10.3390/cryst11060580
Roy D, Clay RT, Mazumdar S. Absence of Superconductivity in the Hubbard Dimer Model for κ-(BEDT-TTF)2X. Crystals. 2021; 11(6):580. https://doi.org/10.3390/cryst11060580
Chicago/Turabian StyleRoy, Dipayan, R. Torsten Clay, and Sumit Mazumdar. 2021. "Absence of Superconductivity in the Hubbard Dimer Model for κ-(BEDT-TTF)2X" Crystals 11, no. 6: 580. https://doi.org/10.3390/cryst11060580
APA StyleRoy, D., Clay, R. T., & Mazumdar, S. (2021). Absence of Superconductivity in the Hubbard Dimer Model for κ-(BEDT-TTF)2X. Crystals, 11(6), 580. https://doi.org/10.3390/cryst11060580