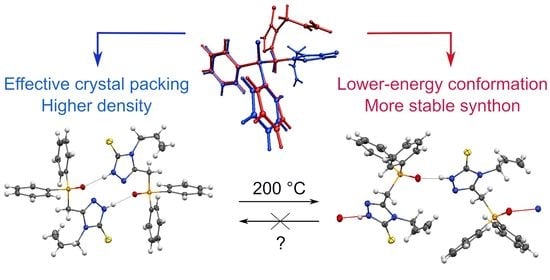
Structures of a Phosphoryl Derivative of 4-Allyl-2,4-dihydro-3H-1,2,4-triazole-3-thione: An Illustrative Example of Conformational Polymorphism

Abstract

Two polymorphic forms of a conformationally flexible molecule, 5-[(Diphenylphosphoryl)methyl]-4-(prop-2-en-1-yl)-2,4-dihydro-3H-1,2,4-triazole-3-thione, were obtained by crystallization and characterized by X-ray diffraction analysis and differential scanning calorimetry. The relative stability of polymorphic forms was estimated with DFT calculations of crystal structures and isolated molecules. It turns out, that in the first more dense polymorph with higher cohesion energy and crystal lattice energy, the molecule adopts an energetically unfavorable conformation, and forms dimers with lower H-bond strength, as compared to the second polymorph. On the other hand, in the second polymorph, the molecule adopts almost the lowest-energy conformation and forms infinite chains via strong H-bonds. The first form that seems to be more thermodynamically stable at room temperature transforms into the second form via two endothermic phase transitions; the apparent irreversibility of the transition is due to high energy difference between the molecular conformations in crystals.

1. Introduction

Despite many years of research, the polymorphism of molecular crystals remains one of the most fascinating and important phenomena in materials science [1]. It is generally believed that nearly any molecule is able to crystallize in more than one polymorphic form, but the effort required to obtain these forms is a priori unknown [2]. Still, the preparation and identification of polymorphs is an important task, as different forms can have different physical properties. Although the fundamental properties of a molecular material are governed mainly by chemical structure and, to a lesser extent, by conformation of the molecule, intramolecular interactions can also play a significant role. Significant difference in dipole moment, strong intramolecular H-bonds, intramolecular charge transfer, etc., are not uncommon for polymorphic forms. Among other substances, for biologically active compounds used as active pharmaceutical ingredients (API), the identification and characterization of polymorphic forms is of particular importance [3]. Indeed, different forms often have different performance characteristics, such as manufacturability (compactability, hardness, tableting, tensile strength, etc.,) and bioavailability (solubility and dissolution rate) [4]. Finally, the discovery of a new form and a failure in the reproducing of previous experiments or spontaneous change of the polymorphic modification of a commercially available drug can lead to its withdrawal from the market [5].

As mentioned above, there is no universal method to predict formation, or to obtain a polymorphic form of an arbitrary compound. However, for particular classes of compounds, there is an enhanced probability of polymorphism. One example is conformational polymorphism [6], the property of conformationally flexible molecules to appear in different conformations in different crystal forms. Although there is no direct relation between the number of conformational degrees of freedom and the number of polymorphic forms, it is evident that the flexibility allows a molecule to adjust its geometry to distinct but equally effective crystal packing patterns. It is also important that intermolecular interactions in crystal can, in principle, not only nearly stabilize isoenergetic conformations, but also conformations that are not favorable for an isolated molecule.

Another factor responsible for the enhanced probability of polymorphism, is the formation of different supramolecular synthons. A supramolecular synthon defined as “a structural unit within supermolecules which can be formed and/or assembled by known or conceivable synthetic operations involving intermolecular interactions” [7] and is one of the most important and fruitful concepts in crystal engineering directly related to polymorphism. Indeed, the formation of different synthons (e.g., dimer vs. chain) automatically leads to different crystal packing [8]. Note that the separation of synthon-forming functional groups by flexible fragments should further increase the probability of polymorphism.

The title compound of this paper (Scheme 1), N-allyl-2,4-dihydro-3H-1,2,4-triazole-3-thione (1), falls into both categories described above. The synthesis of 1 was recently reported by some of us [9], but its crystal structure was unknown. The molecule is conformationally flexible and contains fragments that can participate in strong hydrogen bonds. It is important that 1 is built from moieties that are frequently used in pharmaceutical applications. The substituted 1,2,4-triazole is a part of known compounds with a wide spectrum of biological activity including that which is antimicrobial, antibacterial, analgetic, anticancer, and anti-inflammatory, etc. [10,11,12,13] The phosphoryl group is also not uncommon in drug development [14], and the introduction of this group into the molecule allows for the obtaining of new polyfunctional compounds and the construction of specific supramolecular organization in their crystals. It turns out that 1 crystallizes in two different polymorphic forms, with different conformation and different supramolecular organization. These forms are compared, and their relative stability is discussed.

2. Materials and Methods

2.1. Synthesis and Crystallization

Bulk material (compound 1) was obtained by heterocyclization of the corresponding diphenylphosphorylacetyl thiosemicarbazide by a synthetic method recently developed by some of us [9,15]. Single crystals of first polymorphic modification (1a) suitable for X-ray diffraction were obtained upon cooling a hot saturated solution in dimethyl formamide. The crystals of the same polymorphic form can also be obtained by the same technique from solutions in formic acid, acetic acid, dimethyl formamide, chloroform, dichloroethane, and ethanol mixtures with tetrabutylammonium bromide and tetrabutylammonium iodide. In contrast, very slow crystallization from saturated solution in dimethyl formamide at ambient conditions resulted in the second polymorphic modification (1b).

2.2. Single-Crystal X-ray Crystallography

Single crystal data for polymorph 1a were collected on a Bruker Kappa Apex II CCD automatic diffractometer (graphite monochromator, λ(MoKα) = 0.71073 Å); data collection and unit cell determination were performed using the APEX2 program [16]. The absorption correction was calculated based on the SADABS program [17]. Single crystal data for polymorph 1b were collected on a Rigaku XtaLab Synergy S diffractometer [(λ(CuK_α) = 1.54184 Å]. Data collection, edition, and refinement of unit cell parameters were carried out using the CrysAlisPro program [18], and absorption correction was applied using the SCALE3 ABSPACK algorithm. The structures 1a and 1b were solved by a direct method using SHELXT [19] and refined by the leas-squares technique in the isotropic, first, and then anisotropic approximation (for all non-hydrogen atoms) using SHELXL program [20] integrated in Olex2 package [21]. Coordinates of hydrogen atoms (except those connected nitrogen atoms) were calculated based on stereochemical criteria and refined in the respective riding models. The coordinates of the hydrogen atom H6 of the amino group in crystals of both polymorphs were determined from difference electron density maps and refined in the isotropic approximation. Intermolecular interactions were analyzed, and the figures were drawn using PLATON [22] and Mercury [23] programs. Crystallographic data have been deposited with the Cambridge Crystallography Data Center (CCDC 2104042 and 2104043) and can be obtained by request at www.ccdc.cam.ac.uk/data_request/cif.

2.3. Powder X-ray Diffraction Experiments

Powder XRD patterns were recorded at ambient conditions on a Bruker D8 Advance automatic X-ray diffractometer, equipped with a Vario attachment and a Vantec linear coordinate detector (CuKα₁ radiation, λ = 1.54063 Å, a curved Johansson monochromator; X-ray tube mode was 40 kV and 40 mA). The samples were ground and deposited onto a silicon plate. The diffraction patterns were recorded in the Bragg–Brentano geometry for 2θ ranges of 5–90° or 5–60° with a step size of 0.008° and 4 s per step collection time. The samples were rotated in their planes at a rate of 15 rpm to eliminate the influence of preferred orientation and average data. The PXRD diffraction data were processed using the EVA program package [24] and Bruker TOPAS 5 software [25]. For all PXRD patterns, Pawley refinement was performed; unit cell parameters were refined together with the zero error, adsorption parameters, and background (fitted by a 12-term Chebyshev polynomial).

2.4. Differential Scanning Calorimetry Experiments

DSC measurements were carried out with a DSC 204 F1 Phoenix device (NETZSCH). Experiments were performed in sealed aluminum crucibles with pinhole. Speed of heating was 5 or 10 K⋅min⁻¹. The weight of the samples was about 1–2 mg when measuring the temperature and the enthalpy of transitions.

2.5. Computational Details

Ab initio calculations of crystal structures and their isolated associates were performed with CRYSTAL17 software package [26], commonly used for the density functional theory (DFT) modeling of solid-state 3D structures, but also capable for calculations of 0D and 1D systems. In all calculations, the combination of dispersion-corrected PBE0-D3 functional [27,28] was used in combination with POB-TZVP-rev2 basis set [29] parameterized for calculations of solid-state systems. For both crystal structures, shrinking factor 4 4 4 was used for Monkhorst-Pack grid, yielding in 30 k-points in irreducible Brillouin zone. The known drawback of Gaussian atom-centered method is a basis set superposition error (BSSE) that becomes especially high in crystal structures. Although the POB-TZVP-rev2 basis set was re-parameterized to minimize the BSSE, it still constitutes a large fraction of a lattice energy calculated without a correction (more than 20% in the case of our structures). For this reason, the special algorithms implementing a counterpoise approach [30] for BSSE correction were used: MOLEBSSE keyword for crystal structures and GHOSTS keyword for dimer and chain. In the case of the chain, the additional basis functions (GHOSTS keyword) were placed in the positions of all atoms of the four closest neighboring molecules. Because of BSSE, only atomic coordinates of crystal structures were optimized using experimental unit cell parameters. Although crystal structures were determined at different temperatures, we believe that the energy error introduced by this difference is small.

Topological analysis of the electron density distribution ρ(r) was performed with the TOPOND program [31] integrated in CRYSTAL17. The results of the topological analysis were visualized with AIMStudio program from AIMAll [32] software package, the output files of the TOPOND were converted to sumviz format using an in-house utility topond2 sumviz. To compare the energy of individual bonding interatomic interactions, we used an empirical Espinosa–Molins–Lecomte (EML) correlation [33]: E_EML = −0.5a₀³v(r), where E_EML is interaction energy, a₀ is Bohr radius, and v(r) is potential energy density in a bond critical point. The theoretical justification for this correlation and its possible limitations was proposed [34], but it is known that the values obtained with it cannot be reliable in general due to its empirical nature [35]; for instance, in our experience, the correlation usually significantly underestimates the energy of π–π stacking interactions or overestimated the energies of strong H-bonds. Nevertheless, since it is the only way to estimate the contribution of an individual bonding contact into the interaction energy, we used an EML correlation in this work, but only as supplementary values for those obtained with conventional ab initio calculations.

The search for low-energy conformers of 1 was performed in three steps. At first, a set of 53 molecular geometries was generated with Open Babel program package [36] using the systematic conformer generator and energy cutoff of 6.0 kcal/mol. Then, all generated conformers were optimized at the PBE0-D3/POB-TZVP-rev2 level of theory. On the final step, the set was refined (with obfit program from Open Babel package) to remove coinciding conformers based on their energy and RMS deviation from other conformers. The final set contained 47 distinct conformers.

CrystalExplorer [37] and underlying TONTO programs [38] were used to compute Hirshfeld surfaces (HS) and their associated 2D (two-dimensional) fingerprint plots and calculate interaction energies using a CE-B3LYP method. Note that, despite its name, CE-B3LYP is a semi-empirical approach that only utilizes electron density calculated with B3LYP DFT functional and 6-31G(d) basis set. Lattice energy was calculated from CE-B3LYP method as a sum of pair interaction energies of a central molecule and all symmetry-generated molecules that contained at least one atom within the distance of 20 Å from any atom of the central molecule, divided by a factor of two.

3. Results and Discussion

3.1. Molecular Geometry and Crystal Packing

In attempting to obtain a single crystal of the title compound 1 suitable for structure determination, two polymorphic modifications (1a and 1b) were identified. Note that the crystals of both forms are colorless, have almost the same habit, and are thus nearly indistinguishable in bulk. Two modifications were therefore found quite accidentally by powder diffraction of the samples obtained under different crystallization conditions. The PXRD measurements clearly demonstrated the presence of two distinct pure phases (Figures S1 and S2 in Supplementary Materials). After identification of the polymorphs, the single crystals were grown, and their structures were established by single-crystal X-ray diffraction.

Both forms crystallize in the space group P 2₁/c (see

Table 1. Experimental crystallographic data and refinement parameters for crystals 1a and 1b.

Compound	1a	1b
Chemical formula	C18H18N3OPS
M	355.38
Single-crystal XRD
CCDC number	2104042	2104043
Temperature, K	150	100
Crystal shape, color, size (mm)	colorless block 0.08 × 0.47 × 0.80	colorless prism 0.06 × 0.11 × 0.16
Crystal system, space group	Monoclinic, P 21/c	Monoclinic, P 21/c
Z, Z′	4, 1	4, 1
Unit cell dimension	a = 12.9204(13) Å b = 9.3989(9) Å c = 14.3269(14) Å β = 103.436(5) °	a = 12.9164(3) Å b = 12.6337(2) Å c = 12.0704(3) Å β = 116.155(3) °
Volume, Ǻ3	1692.2 (3)	1767.99 (8)
dcalc, g cm−3	1.395	1.335
Radiation type	MoKα	CuKα
μ (mm−1)	0.296	2.557
2θ range for data collection (°)	5.8–53.7	7.6–152.2
Measured reflections	22,997	20,923
Independent reflections	3614	3654
R(int)	0.0479	0.0515
No. of parameters	221	221
Reflections with I 2σ(I)	3026	3336
R1/wR2 [I > 2σ(I)]	0.0359/0.0876	0.0385/0.1079
R1/wR2 (all reflections)	0.0458/0.0932	0.0417/0.1108
GooF = S	1.051	1.059
ρmax/ρmin (e Ǻ−3)	0.379/−0.329	0.390/−0.427
Powder XRD (Pawley method)
Temperature, K	298	298
Unit cell dimension	a = 12.9709(19) Å b = 9.4680(14) Å c = 14.558(2) Å β = 103.7143(18) °	a = 12.9645 (15) Å b = 12.6921 (16) Å c = 12.1837 (15) Å β = 114.7107 (18) °
Volume, Ǻ3	1736.9(5)	1821.2 (4)
dcalc, g/cm3	1.359	1.296
R(wp)	0.046	0.037

). The structures are a perfect example of confrontational polymorphism, as the difference in molecular conformation in two forms affects the type of the supramolecular synthon found in crystal packing and secondary supramolecular organization.

General view of the molecule 1 in two crystal forms is provided in Figure 1 (see Figure S5 in Supplementary Materials for different molecular projections). The compound 1 itself is conformationally flexible and contains six single rotatable bonds; the torsion angles listed in

Table 2. Selected torsion angles (°) in conformers of 1.

	1a	1b
φ1 (O7-P7-C11-C12)	21.93 (15)	11.72 (15)
φ2 (O7-P7-C17-C18)	41.22 (16)	36.49 (14)
φ3 (O7-P7-C6-C5)	65.16 (15)	−60.78 (12)
φ4 (P7-C6-C5-N4)	−170.98 (13)	84.59 (16)
φ5 (C5-N4-C8-C9)	−84.0 (2)	63.7 (2)
φ6 (N4-C8-C9-C10)	−8.8 (3)	−134.75 (18)

can be used to rationalize the molecular conformation.

The (Ph)₂P(O)C- fragments in polymorphic forms have a similar geometry (Figure 2), with close values of φ₁ and φ₂. The carbon atom C5 of the heterocycle is in synclinal (gauche) position with respect to oxygen atom O7 in both polymorphs. However, in the 1b, the substituent is rotated by ca. 126° about P7-C6 bond relative to 1a, so that the torsions φ₃ have different signs; the resulting orientations are non-equivalent due to their having different positions of the phenyl rings. Further differences are observed for torsion angles φ₄ − φ₆ that are defined formally by sp² and sp³ hybridized atoms. Note that these angles differ significantly in two polymorphs, so that most substituents are in eclipsed conformation relative to the central bond, and two are in staggered positions: the fragments connected to N4-C8 bond in 1a and those connected to C6-C5 bond in 1b. As a result, the overall molecular conformation in 1b looks more “relaxed”, with fewer possible intramolecular distances less than the sum of van der Waals radii [39] of the corresponding elements. Indeed, no non-covalent bonding intramolecular interactions were found in 1b as a bond critical point (BCP) of the electron density in PBE0-D3/POB-TZVP-rev2 optimized structure (Figure S6 in Supplementary Materials). On the other hand, intramolecular bonding interactions were found for pairs O7⋯H8A (experimental distance between the atoms 2.433 Å with C-H set to 1.09 Å), H6B⋯H22 (2.085 Å), H6A⋯C9 (2.634 Å), and S3-H8A (2.705 Å).

Note that, despite the differences in conformation, bond lengths, angles, and torsion angles are within the expected ranges for the corresponding molecular fragments, which is confirmed by a Mogul geometry check [40].

The difference in the molecular conformations of the polymorphs clearly affects the supramolecular organization (Figure 3). While in 1a molecules are connected into centrosymmetric R2,2(14) dimers, the spatial arrangement of donor and acceptor of a H-bond in 1b only allows the formation of infinite H-bonded chains along the crystallographic b axis. The distance between the donor atom O6 and acceptor atom N2 (

Table 3. Geometrical parameters and characteristics of ρ(r) in BCPs for intermolecular H-bonds in polymorphs 1a and 1b.

	Experimental		Crystal DFT a
	1a	1b	1a	1b
N-H b, Å	1.040	1.043	1.040	1.043
N⋯O, Å	2.754 (2)	2.6686 (16)	2.722	2.606
H⋯O, Å	1.727	1.634	1.689	1.569
N-H⋯O,°	168.9	170.8	171.4	172.3
ρ(r), e A−3			0.307	0.393
∇2ρ(r), e A−5			3.33	4.09
EEML, kcal/mol			15.2	21.0

^a Crystal structure optimization with PBE-D3/POB-TZVP-rev2 method: ^b experimental N-H distances were set to values from DFT optimization.

) indicates that the H-bond is significantly stronger in 1b.

It is obvious that the formation of a specific type of supramolecular synthon requires a particular geometric arrangement of functional groups in the molecule. The requirements are apparently somewhat higher for 0D synthons (dimers) than for 1D (chains). In the case of H-bonded synthons, spatial separation of a donor and an acceptor additionally softens the requirement. For instance, many examples of dimers and chains formed by a phosphoryl fragment and an amide or amine group can be found in the Cambridge Structural database (CSD) [41]. However, it is of particular interest when the fragments in the synthon have similar spatial arrangement, as, in this case, synthons resemble biological systems with specific interactions between a receptor and a ligand. Surprisingly, the search of structures with the restrained arrangement of P=O and N-H bonds similar to the one observed in 1a (the “Crystal packing feature” tool in Mercury program, “medium” level of geometric similarity, CSD updates up to May 2021) yielded nine structures. Three of these structures, all benzodiazepine derivatives, are characterized by nearly the same arrangement of donor and acceptor of the H-bond in R2,2(14) cycle as in 1a: CSD ROXRON, ROXRIH, and JUZDOZ (RMS deviation of the distances 0.226, for 0.305, for 0.218 Å). Therefore, even such a complex supramolecular synthon with many bonds between the interacting atoms can be realized in different molecular systems.

3.2. Ab Initio Calculations

To rationalize the differences between the polymorphs on the molecular level, we have performed a series of ab initio calculations of the crystals and isolated systems using the density functional theory (BPE0-D3/POB-TZVP-rev2).

As the molecules in two crystal forms have different conformations, the energy difference between them can play a significant role in determining the relative stability of the forms. First, we compared the energies of the isolated molecules with the geometry taken from the optimized crystal structures or the corresponding polymorphs. It turns out that the molecular conformation in the higher density polymorph 1a is 6.4 kcal/mol less favorable than the conformation in 1b. Geometry optimization starting from these two conformations yielded conformers 1a-opt and 1b-opt with a lower, but still quite high, energy difference of 5.7 kcal/mol. Due to the high conformational lability of 1, it was possible that neither of the two conformers correspond to a global energy minimum. To check this, we performed an exhaustive search of low-energy molecular conformers; in total, 45 distinct conformers were considered in the energy range of 6.4 kcal/mol. It turns out that 1b-opt is almost the lowest-energy conformer, as only one conformer that is lower by 0.33 kcal/mol was found. The energy of this lowest-energy conformer was used to calculate cohesive energy below.

It is obvious that, for two polymorphs to co-exist, the energy difference between the conformers must be compensated by intermolecular interactions. However, the apparently strongest intermolecular interaction, the H-bond, is much shorter in polymorph 1b (with a more favorable molecular conformation); the energy of the H-bond estimated by the EML formula is 5.8 kcal/mol higher for this polymorph (Table 3). However, the difference in bonding energy of the whole synthons (calculated as BSSE-corrected PBE0-D3/POB-TZVP-rev2 energy difference between the synthon and isolated molecule in optimized crystal geometry) is lower and equal to 2.1 kcal/mol (

Table 4. Energetic characteristics (kcal/mol) of crystal structures and supramolecular synthons of 1 calculated with different methods: DFT stands for PBE0-D3/POB-TZVP-rev2 ab initio calculations; CE-B3LYP is semi-empirical approach implemented in CrystaExplorer program; EML is the Espinosa–Molins–Lecomte correlation.

	1a	1b
Cohesive energy (Ecog)
DFT	49.7	46.6
Lattice energy (Elatt)
DFT	60.4	52.0
CE-B3LYP	56.2	45.8
EML	49.7	46.6
Synthon bonding energy (dimer/chain)
DFT	15.9	18.0
CE-B3LYP	12.7	14.2
EML	16.3	23.3

). Similar lower difference of 1.5 kcal/mol between synthon formation energy was obtained by using a completely different semi-empirical CE-B3LYP approach. Topological analysis revealed two additional bonding interactions in dimer and four in chain (Figures S8 and S9 in Supplementary Materials), but the account of the E_EML values of these non-covalent interactions only increases the energy difference between the synthons. It seems that, in case of polymorphs of 1, E_EML significantly overestimates the energy of H-bonds, especially in 1a; however, an important point is that the bonding energy of the supramolecular synthon is still higher in the case of the less dense polymorph 1b.

To our surprise, the cohesive energy (E_cog) of the 1a was calculated to be by 3.1 kcal/mol higher. Although the difference is somewhat higher than normally expected for polymorphic forms, it is partly compensated by the thermal effects of endothermic phase transition (see below), but can also be related to the imperfection of the DFT method used for calculations. Nevertheless, the calculated energy difference between the forms is consistent with Kitaigorodskii’s principle of close packing [42], as 1a is denser than 1b at low temperatures as well as at ambient conditions.

Another indicative quantity is the lattice energy (E_latt), calculated as BSSE-corrected energy difference between the total energy (E_tot) of the crystal and the energy of the isolated molecule with the geometry taken from crystal structure. The value of E_latt calculated by PBE0-D3/POB-TZVP-rev2 is by 9.6 kcal/mol higher for 1a. The similar difference in E_latt equal to 10.4 kcal/mol is calculated by a completely different CE-B3LYP semi-empirical approach. Higher values of E_latt for 1a not only confirm its higher stability, but also indicate more effective crystal packing for this polymorphic form compared to 1b. Apparently high differences in E_latt are partly compensated by energy differences between molecular conformations in the crystals described above.

All bonding intermolecular interactions were found as bond critical points (BCPs) of ρ(r) obtained from DFT calculations (Tables S2 and S3 in Supplementary Materials). It should be noted that the geometry optimization of crystal structures leads to slightly different distances between the interacting atoms, as compared to experimental data. For instance, the strength of H-bonds seems to be overestimated by DFT. In addition, the values of E_EML seems to be unreliable for H-bonds, as described above. However, even a qualitative analysis of intermolecular BCPs shows a key difference between the polymorphs. It was found that the number of intermolecular BCPs in 1a (33) is significantly higher than in 1b (23). This is more evidence of another effective crystal packing of the form 1b and just another example of the rule: “crystals with a few strong and many weaker interactions are less dense and, in general, less stable than similar crystal structures with many interactions of the average strength” (for several other recent justifications of this rule, see, e.g., [43,44]). Moreover, note that, despite EML correlation overestimating the energy of H-bond in 1b, the lattice energy of this polymorph calculated as the sum of E_EML values of all individual interactions is lower than that for 1b.

3.3. Differential Scanning Calorimetry Experiments

The thermochemical behavior of two polymorphs was studied by differential scanning calorimetry. According to the obtained DSC data for the two crystal samples, melting peaks with the close thermochemical parameters (temperature, enthalpy) are observed at a temperature about 240 °C (Figure 4). However, sample 1a undergoes a number of transformations, therefore the observed peak of the melting could not be directly related to the melting temperature of the 1a polymorph.

The thermogram for 1b shows the well-defined endothermic peak of melting to be about 239 °C (enthalpy of melting 6.79 kcal/mol). The non-ideal shape of peak—stretched leading front and shift of the baseline after the completion of the melting to the exothermic area—may be caused by the decomposition of the substance while under the melting temperature (Figure 4, blue curve).

In contrast, 1a polymorph exhibited a more complex behavior, namely, three sequential endothermic events on the curve (Figure 4, red curve). The first one at about 150 °C has an irregular, complex shape (full enthalpy of effect about 0.67 kcal/mol). At this point, 1a undergoes some transformation with the formation of intermediate phase that exists only in this temperature range of 160–180 °C. It is rather difficult to study this phase by another physical technique because, after cooling, we observe the reversible process with the lowest hysteresis on a temperature scale (Figure 4, magenta and dark cyan curves). The complex shape of the peak indicates that corresponding process occurs in several stages. After heating to 170 and cooling back to room temperature, the phase coincides with the source 1a (see Figure S3 in Supplementary Materials).

One more endothermic process is observed at about 180 °C (full enthalpy of effect about 1.36 kcal/mol). On further heating, the sample melts and the thermochemical parameters of its melt process are close to those for 1b polymorph. This allows us to assume that the endothermic event observed at temperatures above 180 °C corresponds to the irreversible solid-state transformation between different forms of the compound 1. The experimental powder diffractogram for the 1a heated until 200 °C and cooled corresponds with the theoretical powder diffractogram of 1b (see Figure S4 in Supplementary Materials).

Thus, we established two solid-state transformations for compound 1. At first, it is a reversible enantiotropic transition between polymorph 1a and some intermediate phase at about 150 °C. Second, a monotropic transition is observed between intermediate phase and 1b at about 180 °C. Based on DSC data, 1b polymorph is a thermodynamic form for compound 1 at temperatures above the second phase transition of 1a, but not at room temperatures, as both phase transitions are endothermic.

4. Conclusions

To summarize, two conformational polymorphs of a conformationally labile compound, 5-[(Diphenylphosphoryl)methyl]-4-(prop-2-en-1-yl)-2,4-dihydro-3H-1,2,4-triazole-3-thione 1, were obtained by different crystallization methods and fully characterized with X-ray diffraction methods and through differential scanning calorimetry. The molecule in polymorphs form different supramolecular synthons via strong N-H···O hydrogen bonds, a dimer in 1a and H-bonded chain in 1b. It turns outs that the polymorph 1a, which is characterized by higher density both at low and room temperature, undergoes an irreversible phase transition to phase 1b when heated to 200 °C. However, both phase transitions preceding the transformation are endothermic, which indicates the higher stability of 1a at room temperature. Ab initio calculations of crystal structures, isolated associates, and different conformations of 1 confirms that 1a has lower cohesive and lattice energy, while in crystal 1b, the molecule has a significantly more favorable conformation and forms a supramolecular synthon with higher bonding energy. The energy difference of ca. 6 kcal/mol between molecular conformations in the crystals of polymorphs can explain the apparent irreversibility of phase transition, as the reverse process requires significant energetically unfavorable change in molecular conformation. On the other hand, we can speculate that the crystallization from the hot solution that leads to 1a probably provides, together with solvation effects, the required population of the corresponding molecular conformation during the nucleation and crystal growth.