Cocrystal Prediction Based on Deep Forest Model—A Case Study of Febuxostat
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset Building
- Containing only two chemically distinct polyatomic units.
- Removing samples without a clear structure.
- Containing only C, H, O, N, P, S, Cl, Br, I, F, Si, and halogen elements, no metal elements.
- Molecular weight of each component <700.
- Neutral molecule without salt.
- Deleting duplicate records.
- Not containing any common solvents or gas molecules [14] (Reference application literature list).
2.2. Feature Representation of the Sample
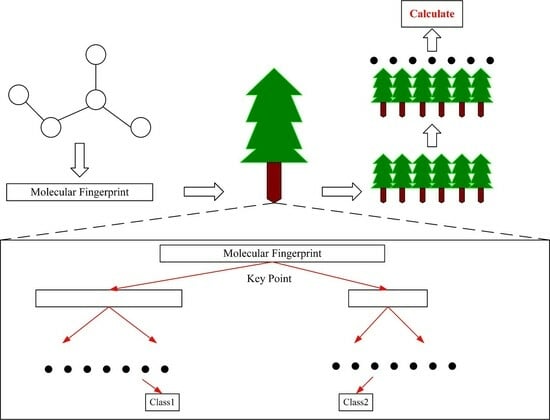
2.3. Prediction Model
2.4. Evaluation Methodology
2.5. Febuxostat Cocrystal Screening Methodology
3. Results
3.1. Model Selection and Performance Testing
3.2. Case Study of Febuxostat
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.; Wang, X.; Yu, D.; Zhoujin, Y.; Wang, K. Molecular complexes of drug combinations: A review of cocrystals, salts, coamorphous systems and amorphous solid dispersions. Int. J. Pharm. 2023, 648, 123555. [Google Scholar] [CrossRef] [PubMed]
- Putra, O.D.; Furuishi, T.; Yonemochi, E.; Terada, K.; Uekusa, H. Drug-drug multicomponent crystals as an effective technique to overcome weaknesses in parent drugs. Cryst. Growth Des. 2016, 16, 3577–3581. [Google Scholar] [CrossRef]
- Alsubaie, M.; Aljohani, M.; Erxleben, A.; McArdle, P. Cocrystal forms of the BCS class IV drug sulfamethoxazole. Cryst. Growth Des. 2018, 18, 3902–3912. [Google Scholar] [CrossRef]
- Barua, H.; Gunnam, A.; Yadav, B.; Nangia, A.; Shastri, N.R. An ab initio molecular dynamics method for cocrystal prediction: Validation of the approach. CrystEngComm 2019, 21, 7233–7248. [Google Scholar] [CrossRef]
- Hollingsworth, S.A.; Dror, R.O. Molecular dynamics simulation for all. Neuron 2018, 99, 1129–1143. [Google Scholar] [CrossRef] [PubMed]
- Balmohammadi, Y.; Grabowsky, S. Arsenic-Involving Intermolecular Interactions in Crystal Structures: The Dualistic Behavior of As (III) as Electron-Pair Donor and Acceptor. Cryst. Growth Des. 2023, 23, 1033–1048. [Google Scholar] [CrossRef]
- Grecu, T.; Hunter, C.A.; Gardiner, E.J.; McCabe, J.F. Validation of a computational cocrystal prediction tool: Comparison of virtual and experimental cocrystal screening results. Cryst. Growth Des. 2014, 14, 165–171. [Google Scholar] [CrossRef]
- Ryan, K.; Lengyel, J.; Shatruk, M. Crystal structure prediction via deep learning. J. Am. Chem. Soc. 2018, 140, 10158–10168. [Google Scholar] [CrossRef]
- Wicker, J.G.P.; Crowley, L.M.; Robshaw, O.; Little, E.J.; Stokes, S.P.; Cooper, R.I.; Lawrence, S.E. Will they co-crystallize? CrystEngComm 2017, 19, 5336–5340. [Google Scholar] [CrossRef]
- Wang, D.; Yang, Z.; Zhu, B.; Mei, X.; Luo, X. Machine-Learning-Guided Cocrystal Prediction Based on Large Data Base. Cryst. Growth Des. 2020, 20, 6610–6621. [Google Scholar] [CrossRef]
- Devogelaer, J.J.; Meekes, H.; Tinnemans, P.; Vlieg, E.; de Gelder, R. Co-crystal prediction by artificial neural networks. Angew. Chem. Int. Ed. 2020, 59, 21711–21718. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Feng, J. Deep forest. Natl. Sci. Rev. 2019, 6, 74–86. [Google Scholar] [CrossRef] [PubMed]
- Allen, F.H.; Taylor, R. Research applications of the Cambridge structural database (CSD). Chem. Soc. Rev. 2004, 33, 463–475. [Google Scholar] [CrossRef] [PubMed]
- Devogelaer, J.-J.; Brugman, S.J.T.; Meekes, H.; Tinnemans, P.; Vlieg, E.; de Gelder, R. Cocrystal design by network-based link prediction. CrystEngComm 2019, 21, 6875–6885. [Google Scholar] [CrossRef]
- Liu, H.; Sun, J.; Guan, J.; Zheng, J.; Zhou, S. Improving compound–protein interaction prediction by building up highly credible negative samples. Bioinformatics 2015, 31, i221–i229. [Google Scholar] [CrossRef] [PubMed]
- Ferrence, G.M.; Tovee, C.A.; Holgate, S.J.; Johnson, N.T.; Lightfoot, M.P.; Nowakowska-Orzechowska, K.L.; Ward, S.C. CSD Communications of the Cambridge Structural Database. IUCrJ 2023, 10, 6–15. [Google Scholar] [CrossRef] [PubMed]
- Bennion, J.C.; Matzger, A.J. Development and evolution of energetic cocrystals. Acc. Chem. Res. 2021, 54, 1699–1710. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Chen, T.; Minami, M. Intelligent fault prediction system based on internet of things. Comput. Math. Appl. 2012, 64, 833–839. [Google Scholar] [CrossRef]
- Tao, Y.; Papadias, D. Maintaining sliding window skylines on data streams. IEEE Trans. Knowl. Data Eng. 2006, 18, 377–391. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rätsch, G.; Onoda, T.; Müller, K.R. Soft margins for AdaBoost. Mach. Learn. 2001, 42, 287–320. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chebil, W.; Wedyan, M.; Alazab, M.; Alturki, R.; Elshaweesh, O. Improving Semantic Information Retrieval Using Multinomial Naive Bayes Classifier and Bayesian Networks. Information 2023, 14, 272. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. In Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Curran Associates Inc.: Red Hook, NY, USA, 2019. [Google Scholar]
- Landrum, G. RDKit: A software suite for cheminformatics, computational chemistry, and predictive modeling. Greg Landrum 2013, 8, 31. [Google Scholar]
- Rigaku. PROCESS-AUTO; Rigaku Corporation: Tokyo, Japan, 1998. [Google Scholar]
- Rigaku. CrystalStructure; Version 3.8.0; Rigaku Corporation: Tokyo, Japan; Rigaku Americas: The Woodlands, TX, USA, 2007. [Google Scholar]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. A 2008, 64, 112–122. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. In Advances in Neural Information Processing Systems 30 (NIPS 2017), Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017. [Google Scholar]
- Kang, Y.; Gu, J.; Hu, X. Syntheses, structure characterization and dissolution of two novel cocrystals of febuxostat. J. Mol. Struct. 2017, 1130, 480–486. [Google Scholar] [CrossRef]
- Shin, H.C.; Roth, H.R.; Gao, M.; Lu, L.; Xu, Z.; Nogues, I.; Yao, J.; Mollura, D.; Summers, R.M. Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning. IEEE Trans. Med. Imaging 2016, 35, 1285–1298. [Google Scholar] [CrossRef]
- Kovács, I.A.; Luck, K.; Spirohn, K.; Wang, Y.; Pollis, C.; Schlabach, S.; Bian, W.; Kim, D.-K.; Kishore, N.; Hao, T.; et al. Network-based prediction of protein interactions. Nat. Commun. 2019, 10, 1240. [Google Scholar] [CrossRef]
- Chalkha, M.; El Hassani, A.A.; Nakkabi, A.; Tüzün, B.; Bakhouch, M.; Benjelloun, A.T.; Sfaira, M.; Saadi, M.; El Ammari, L.; El Yazidi, M. Crystal structure, Hirshfeld surface and DFT computations, along with molecular docking investigations of a new pyrazole as a tyrosine kinase inhibitor. J. Mol. Struct. 2023, 1273, 134255. [Google Scholar] [CrossRef]








| Information about Molecular Fingerprints | Length (Bits) | Emphasis |
|---|---|---|
| MACCS | 166 | substructure |
| RDKit | 2048 | molecular structure |
| ECFP4 | 2048 | atomic radius |
| FCFP4 | 2048 | atomic properties |
| Fingerprint Type | Accuracy |
|---|---|
| MACCS add | 95.26% |
| MACCS connect | 94.92% |
| RDKit add | 94.19% |
| RDKit connect | 94.03% |
| ECFP4 add | 95.51% |
| ECFP4 connect | 95.35% |
| FCFP4 add | 95.16% |
| FCFP4 connect | 94.24% |
| ECFP4 | FCFP4 | MACCS | RDKit | |
|---|---|---|---|---|
| Accuracy | 95.51% | 95.16% | 95.26% | 94.19% |
| Precision | 94.03% | 94.42% | 94.55% | 94.21% |
| Recall | 95.75% | 95.26% | 93.23% | 95.09% |
| Sensitivity | 97.82% | 97.46% | 97.57% | 96.83% |
| Specificity | 95.26% | 95.31% | 95.14% | 95.13% |
| Average | 95.67% | 95.52% | 95.15% | 95.09% |
| RF | Deep Forest | Deep Forest (LightGBM) | |
|---|---|---|---|
| Accuracy | 82.93% | 95.51% | 96.15% |
| Precision | 82.41% | 94.03% | 94.85% |
| Recall | 83.96% | 95.75% | 96.69% |
| Sensitivity | 92.52% | 97.82% | 97.91% |
| Specificity | 72.76% | 95.26% | 95.83% |
| Empirical Formula | C16H16N2O3S ▪ C6H6N2O | X-ray Wavelength | 0.71073 Å |
|---|---|---|---|
| Formula weight | 438.49 | Range h | −10 to 10 |
| Crystal system | Monoclinic | Range k | −36 to 36 |
| Space group | P 21/n | Range l | −12 to 12 |
| T (K) | 296(2) | Reflections collected | 12,542 |
| a (Å) | 8.2879(4) | Total reflections | 4931 |
| b (Å) | 28.2769(10) | Observed reflections | 3022 |
| c (Å) | 9.6578(4) | R[I > 2σ(I)] | 0.0948 |
| α (°) | 90 | (∆/σ) max | 0.000 |
| β (°) | 106.943 | S | 1.011 |
| γ (°) | 90 | Rint | 0.0607 |
| V (Å3) | 2165.12 | wR (F2) | 0.1304 |
| θ range | 3.1–27.5 | Goodness of fit | 1.011 |
| Z | 4 | Diffractometer | Rigaku RAXIS-RAPID |
| Crystal size (mm) | 0.43 × 0.23 × 0.18 | Refinement method | full-matrix least-squares on F2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Li, Z.; Kang, Y.; Li, Z. Cocrystal Prediction Based on Deep Forest Model—A Case Study of Febuxostat. Crystals 2024, 14, 313. https://doi.org/10.3390/cryst14040313
Chen J, Li Z, Kang Y, Li Z. Cocrystal Prediction Based on Deep Forest Model—A Case Study of Febuxostat. Crystals. 2024; 14(4):313. https://doi.org/10.3390/cryst14040313
Chicago/Turabian StyleChen, Jiahui, Zhihui Li, Yanlei Kang, and Zhong Li. 2024. "Cocrystal Prediction Based on Deep Forest Model—A Case Study of Febuxostat" Crystals 14, no. 4: 313. https://doi.org/10.3390/cryst14040313
APA StyleChen, J., Li, Z., Kang, Y., & Li, Z. (2024). Cocrystal Prediction Based on Deep Forest Model—A Case Study of Febuxostat. Crystals, 14(4), 313. https://doi.org/10.3390/cryst14040313