X-ray Diffraction: A Powerful Technique for the Multiple-Length-Scale Structural Analysis of Nanomaterials
Abstract
:1. Why X-rays
2. Nanomaterials and X-rays
- -
- crystal atomic structure: positions/symmetry of the atoms in the unit cell, unit cell size, size/shape of the nanocrystalline domain;
- -
- crystalline mixture: identification of the crystalline phases and quantitative determination of their weight fractions;
- -
- nanoscale assembly: positions/symmetry of the nanoparticles/nanocrystals in the assembly and extension of the assembly.
3. Thomson/Rayleigh Scattering and Structure Factor
4. Planning an Experiment: Small or Wide Angle? Bragg Diffraction or Scattering?
5. A Laboratory Set Up: The XMI-L@b for SAXS/WAXS or GISAXS/GIWAXS Data Collection
6. Applications
- -
- Combined SAXS and WAXS analysis (Figure 5) allowed us to determine independently particle size/shape and crystalline domain size of silver nanoparticles, dispersed in water. Indeed, nanoparticles can be amorphous, single or multiple crystalline domains. Measuring only SAXS data cannot discriminate between these possibilities. Only the combination of these two techniques can provide a complete answer.
- -
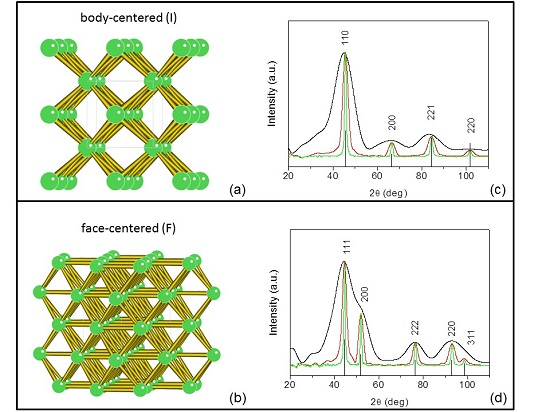
- X-ray diffraction (Figure 6) from nanocrystalline powders allowed us to attribute the proper crystal lattice, to refine the lattice unit cell size, to evaluate the crystalline lattice coherence (crystal habit).
- -
- X-ray microdiffraction from bone tissues (Figure 7a–e) was used to identify the hydroxyapatite (HA) crystal structure and to map the orientation of the HA nanocrystals with respect to the collagen fibers.
- -
- X-ray diffraction (Figure 7f,g) was a means to select and quantify the polymorphs composing a nanocrystalline TiO2 powder.
- -
- WAXS/atomic PDF analysis (Figure 8) of a tungsten oxide nanomaterial was performed to identify the actual crystalline structure among competitive Magnéli phases.
- -
- GISAXS and GIWAXS techniques (Figure 9) were chosen to inspect the nanoscale and atomic order of self-assembled 2D or 3D nanocrystal superlattices, respectively.
- -
7. Nanoparticles in Water
8. Nanocrystalline Powders
- -
- crystalline structure
- -
- crystalline domain size
- -
- multiple crystalline phases
- -
- possible preferred orientations
9. Nano-Structured Surfaces
- Forces of chemical bonding (covalent, ionic, van der Waals, hydrogen)
- Physical forces (magnetic, electrostatic, fluidic, ...)
- Polar/Nonpolar (hydrophobicity)
- Shape (configurational)
- Templates (guided self-assembly)
10. Nanomaterials in Polymers
11. Conclusions and Perspectives
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Attwood, D. Soft X-rays and Extreme Ultraviolet Radiation; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Als-Nielsen, J.; McMorrow, D. Elements of Mondern. X-ray Optics; John Wiley & Sons, Ltd.: Chichester, UK, 2000. [Google Scholar]
- Arfelli, F.; Bonvicini, V.; Bravin, A.; Cantatore, G.; Castelli, E.; Palma, L.D.; Michiel, M.D.; Fabrizioli, M.; Longo, R.; Menk, R.H.; et al. Mammography with synchrotron radiation: Phase-detection techniques. Radiology 2000, 215, 286–293. [Google Scholar] [CrossRef] [PubMed]
- Ambrose, J. Computerized transverse axial scanning (tomography): Part 2. Clinical application. Br. J. Radiol. 1973, 46, 1023–1047. [Google Scholar] [CrossRef] [PubMed]
- Peterson, V.K.; Papadakis, C.M. Functional materials analysis using in situ and in operando X-ray and neutron scattering. IUCr J. 2015, 2, 292–304. [Google Scholar] [CrossRef] [PubMed]
- Lamberti, C.; Bordiga, S.; Bonino, F.; Prestipino, C.; Berlier, G.; Capello, L.; D’Acapito, F.; Llabre´s Xamena, F.X.; Zecchina, A. Determination of the oxidation and coordination state of copper on different Cu-based catalysts by XANES spectroscopy in situ or in operando conditions. Phys. Chem. Chem. Phys. 2003, 5, 4502–4509. [Google Scholar] [CrossRef]
- Metzger, T.; Favre-Nicolin, V.; Renaud, G.; Renevier, H.; Schülli, T. Nanostructures in the Light of Synchrotron Radiation: Surface-Sensitive X-ray Techniques and Anomalous Scattering. In Characterization of Semiconductor Heterostructures and Nanostructures; Elsevier: Oxford, UK, 2008. [Google Scholar]
- Zanchet, D.; Hall, B.D.; Ugarte, D. X-ray Characterization of Nanoparticles. In Characterization of Nanophase Materials; Wiley: Atlanta, GA, USA, 2001. [Google Scholar]
- Altamura, D.; Sibillano, T.; Siliqi, D.; De Caro, L.; Giannini, C. Grazing Incidence X-ray Studies of Assembled Nanostructured Architectures. Nanomater. Nanotechnol. 2012, 2, Art.16:2012. [Google Scholar]
- Miao, J.; Ishikawa, T.; Shen, Q.; Earnest, T. Extending X-ray Crystallography to Allow the Imaging of Noncrystalline Materials, Cells, and Single Protein Complexes. Annu. Rev. Phys. Chem. 2008, 59, 387–410. [Google Scholar] [CrossRef] [PubMed]
- Robinson, I.; Harder, R. Coherent X-ray diffraction imaging of strain at the nanoscale. Nat. Mater. 2009, 8, 291–298. [Google Scholar] [CrossRef] [PubMed]
- Thibault, P.; Elser, V. X-ray Diffraction Microscopy. Annu. Rev. Condens. Matter Phys. 2010, 1, 237–255. [Google Scholar] [CrossRef]
- Holt, M.; Harder, R.; Winarski, R.; Rose, V. Nanoscale Hard X-ray Microscopy Methods for Materials Studies. Annu. Rev. Mater. Res. 2013, 43, 183–211. [Google Scholar] [CrossRef]
- Rao, C.N.R.; Biswas, K. Characterization of Nanomaterials by Physical Methods. Annu. Rev. Anal. Chem. 2009, 2, 435–462. [Google Scholar] [CrossRef] [PubMed]
- Dorfs, D.; Krahne, R.; Giannini, C.; Falqui, A.; Zanchet, D.; Manna, L. Quantum Dots: Synthesis and Characterization. In Comprehensive Nanoscience and Technology; Elsevier: London, UK, 2011. [Google Scholar]
- Garti, N.; Somasundaran, P.; Mezzenga, R. Self-Assembled Supramolecular Architectures: Lyotropic. Liquid Crystals; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Grünwald, M.; Geissler, P.L. Patterns without Patches: Hierarchical Self-Assembly of Complex Structures from Simple Building Blocks. ACS Nano 2014, 8, 5891–5897. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Sun, Z.; Dou, Y.; Kim, J.H.; Dou, S.X. Two-step self-assembly of hierarchically-ordered nanostructures. J. Mater. Chem. A 2015, 3, 11688–11699. [Google Scholar] [CrossRef]
- Ozin, G.A.; Hou, K.; Lotsch, B.V.; Cademartiri, L.; Puzzo, D.P.; Scotognella, F.; Ghadimi, A.; Thomson, J. Nanofabrication by Self-assembly. Mater. Today 2009, 12, 12–23. [Google Scholar] [CrossRef]
- Keys, A.S.; Iacovella, C.R.; Glotzer, S.C. Characterizing Structure Through Shape Matching and Applications to Self-Assembly. Annu. Rev. Condens. Matter Phys. 2011, 2, 263–285. [Google Scholar] [CrossRef]
- Thiruvengadathan, R.; Korampally, V.; Ghosh, A.; Chanda, N.; Gangopadhyay, K.; Gangopadhyay, S. Nanomaterial processing using self-assembly-bottom-up chemical and biological approaches. Rep. Prog. Phys. 2013, 76, 066501. [Google Scholar] [CrossRef] [PubMed]
- Murray, C.B.; Kagan, C.R.; Bawendi, M.G. Synthesis and characterization of monodisperse nanocrystals and close-packed nanocrystal assemblies. Annu. Rev. Mater. Sci. 2000, 30, 545–610. [Google Scholar] [CrossRef]
- Giacovazzo, C.; Monaco, H.L.; Viterbo, D.; Scordari, F.; Gilli, G.; Zanotti, G.; Catti, M. Fundamentals of Crystallography; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Landau, L.D.; Lifshitz, L.M. Quantum Mechanics, Non-Relativistic Theory 3; Pergamon Press: Oxford, UK, 1977. [Google Scholar]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Abrikosov, A.A.; Gor’kov, L.P.; Dzialoskinskii, I.E. Methods of Quantum Field Theory in Statistical Physics; Dover Publications: Dover, NY, USA, 1994. [Google Scholar]
- Thomas, L.H.; Umeda, K. Atomic Scattering Factors Calculated from the TFD Atomic Model. J. Chem. Phys. 1957, 26, 293. [Google Scholar] [CrossRef]
- Cromer, D.T.; Mann, J.B. X-ray scattering factors computed from numerical Hartree-Fock wave functions. Acta Cryst. 1968, A24, 321–328. [Google Scholar] [CrossRef]
- James Holton. Available online: http://bl831.als.lbl.gov/~jamesh/ (accessed on 26 July 2016).
- Bilbao Crystallographic Server. Available online: http://www.cryst.ehu.es/ (accessed on 26 July 2016).
- Confalonieri, G.; Dapiaggi, M.; Sommariva, M.; Gateshki, M.; Fitch, A.N.; Bernasconi, A. Comparison of total scattering data from various sources: The case of a nanometric spinel. Powder Diffr. 2015, 30, S65–S69. [Google Scholar] [CrossRef]
- Dykhne, T.; Taylor, R.; Florence, A.; Billinge, S.J. Data requirements for the reliable use of atomic pair distribution functions in amorphous pharmaceutical fingerprinting. Pharm. Res. 2011, 28, 1041–1048. [Google Scholar] [CrossRef] [PubMed]
- Margaritondo, G. Introduction to Synchrotron Radiation; Oxford: New York, NY, USA, 1988. [Google Scholar]
- Reiss, C.A.; Kharchenko, A.; Gateshki, M. On the use of laboratory X-ray diffraction equipment for Pair Distribution Function (PDF) studies. Z. Kristallogr. 2012, 227, 257–261. [Google Scholar] [CrossRef]
- Craievich, A.F. Small angle X-ray scattering by nanostructured materials. In Handbook of Sol-Gel Science and Technology, 1st ed.; Sakka, A., Almeida, R., Eds.; Kluwer Publishers: Norwell, MA, USA, 2005; pp. 161–189. [Google Scholar]
- Renaud, G.; Lazzari, R.; Leroy, F. Probing surface and interface morphology with Grazing Incidence Small Angle X-ray Scattering. Surf. Sci. Rep. 2009, 64, 255–380. [Google Scholar] [CrossRef]
- Altamura, D.; Lassandro, R.; De Caro, L.; Siliqi, D.; Ladisa, M.; Giannini, C. X-ray MicroImaging Laboratory (XMI-LAB). J. Appl. Cryst. 2012, 45, 869–873. [Google Scholar] [CrossRef]
- Sibillano, T.; De Caro, L.; Altamura, D.; Siliqi, D.; Ramella, M.; Boccafoschi, F.; Ciasca, G.; Campi, G.; Tirinato, L.; Di Fabrizio, E.; et al. An Optimized Table-Top Small-Angle X-ray Scattering Set-up for the Nanoscale Structural Analysis of Soft Matter. Sci. Rep. 2014, 4, 6985. [Google Scholar] [CrossRef] [PubMed]
- Zheng, N.; Yi, Z.; Li, Z.; Chen, R.; Lai, Y.; Men, Y. Achieving grazing-incidence ultra-small-angle X-ray scattering in a laboratory setup. J. Appl. Cryst. 2015, 48, 608–612. [Google Scholar] [CrossRef]
- Kirkpatrick, P.; Baez, A.V. Formation of optical images by X-rays. J. Opt. Soc. Am. 1948, 38, 766–774. [Google Scholar] [CrossRef] [PubMed]
- Mills, D.; Padmore, H. Report of the Basic Energy Sciences Workshop on X-ray Optics for BES Light Source Facilities. Available online: http://science.energy.gov/bes/community-resources/reports/ (accessed on 26 July 2016).
- Corricelli, M.; Altamura, D.; Curri, M.L.; Sibilano, T.; Siliqi, D.; Mazzone, A.; Depalo, N.; Fanizza, E.; Zanchet, D.; Giannini, C.; Striccoli, M. GISAXS and GIWAXS study on self-assembling processes of nanoparticle based superlattices. CrystEngComm 2014, 16, 9482–9492. [Google Scholar] [CrossRef]
- De Caro, L.; Altamura, D.; Sibillano, T.; Siliqi, D.; Filograsso, G.; Bunk, O.; Giannini, C. Rat-tail tendon fiber SAXS high-order diffraction peaks recovered by a superbright laboratory source and a novel restoration algorithm. J. Appl. Cryst. 2013, 46, 672–678. [Google Scholar] [CrossRef]
- Hemberg, O.; Otendal, M.; Hertz, H.M. Liquid-metal-jet anode electron-impact X-ray source. Appl. Phys. Lett. 2003, 83, 1483. [Google Scholar] [CrossRef]
- Li, Y.; Beck, R.; Huang, T.; Choi, M.C.; Divinagracia, M. Scatterless hybrid metal-single-crystal slit for small-angle X-ray scattering and high-resolution X-ray diffraction. J. Appl. Cryst. 2008, 41, 1134–1139. [Google Scholar] [CrossRef]
- Kraft, P.; Bergamaschi, A.; Broennimann, C.; Dinapoli, R.; Eikenberry, E.F.; Henrich, B.; Johnson, I.; Mozzanica, A.; Schlepütz, C.M.; Willmott, P.R.; et al. Performance of single-photon-counting PILATUS detector modules. J. Synch. Rad. 2009, 16, 368–375. [Google Scholar] [CrossRef] [PubMed]
- Johnson, I.; Bergamaschi, A.; Buitenhuis, J.; Dinapoli, R.; Greiffenberg, D.; Henrich, B.; Ikonen, T.; Meier, G.; Menzel, A.; Mozzanica, A.; et al. Capturing dynamics with Eiger, a fast-framing X-ray detector. J. Synch. Rad. 2012, 19, 1001–1005. [Google Scholar] [CrossRef] [PubMed]
- Campbell, M. 10 years of the Medipix2 Collaboration. Nucl. Instr. Meth. A 2011, 633, S1–S10. [Google Scholar] [CrossRef]
- Svergun, D.I. Determination of the regularization parameter in indirect-transform methods using perceptual criteria. J. Appl. Cryst. 1992, 25, 495–503. [Google Scholar] [CrossRef]
- Egami, T.; Billinge, S.J.L. Underneath the Bragg Peaks—Structural Analysis of Complex Materials; Pergamon: London, UK, 2012. [Google Scholar]
- Glatter, O. The interpretation of real-space information from small-angle scattering experiments. J. Appl. Cryst. 1979, 12, 166–175. [Google Scholar] [CrossRef]
- Glatter, O. Determination of particle-size distribution functions from small-angle scattering data by means of the indirect transformation method. J. Appl. Cryst. 1980, 13, 7–11. [Google Scholar] [CrossRef]
- Giannini, C.; Siliqi, D.; Altamura, D. Nanomaterial Characterization By X-Ray Scattering Techniques. In Nanocomposites: In Situ Synthesis of Polymer-Embedded Nanostructures; Wiley: Oboken, NJ, USA, 2013. [Google Scholar]
- ImageJ—Image Processing and Analysis in Java. Available online: https://imagej.nih.gov/ij/ (accessed on 26 July 2016).
- Rodriguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Franke, D.; Svergun, D.I. DAMMIF, a program for rapid ab-initio shape determination in small-angle scattering. J. Appl. Cryst. 2009, 42, 342–346. [Google Scholar]
- Straumanis, M.E.; Yu, L.S. Lattice parameters, densities, expansion coefficients and perfection of structures of Cu and Cu-In alpha phase. Acta. Cryst. A 1969, 25, 676–682. [Google Scholar] [CrossRef]
- Massarotti, V.; Capsoni, D.; Bini, M.; Altomare, A.; Moliterni, A.G.G. X-ray powder diffraction ab initio structure solution of materials from solid state synthesis: The copper oxide case. Z. Kristallogr. 1998, 213, 259–265. [Google Scholar] [CrossRef]
- Petronella, F.; Curri, M.L.; Striccoli, M.; Mateo-Mateo, C.; Alvarez-Puebla, R.A.; Sibillano, T.; Giannini, C.; Correa-Duarte, M.A.; Comparelli, R. Direct growth of shape controlled TiO2 nanocrystals onto SWCNTs for highly active photocatalytic materials in the visible. Appl. Cat. B: Environ. J. 2015, 178, 91–99. [Google Scholar] [CrossRef]
- Lynch, J.; Giannini, C.; Cooper, J.; Sharp, J.; Buonsanti, R. Substitutional or interstitial site-selective nitrogen doping in TiO2 nanostructures. J. Phys. Chem. C 2015, 119, 7443–7452. [Google Scholar] [CrossRef]
- Kay, M.I.; Young, R.A.; Posner, A.S. Crystal structure of hydroxyapatite. Nature 1964, 25, 1050–1052. [Google Scholar] [CrossRef]
- Giannini, C.; Siliqi, D.; Bunk, O.; Beraudi, A.; Ladisa, M.; Altamura, D.; Stea, S.; Baruffaldi, F. Correlative light and scanning X-ray Scattering microscopy of healthy and pathologic human bone sections. Sci. Rep. 2012, 2, 435. [Google Scholar] [CrossRef] [PubMed]
- Vittadini, A.; Sedona, F.; Agnoli, S.; Artiglia, L.; Casarin, M.; Rizzi, G.A.; Sambi, M.; Granozzi, G. Stability of TiO2 Polymorphs: Exploring the Extreme Frontier of the Nanoscale. Chemphyschem 2010, 11, 1550–1557. [Google Scholar] [CrossRef] [PubMed]
- Caliandro, R.; Sibillano, T.; Belviso, B.D.; Scarfiello, R.; Hanson, J.C.; Dooryhee, E.; Manca, M.; Cozzoli, P.D.; Giannini, C. Static and dynamical structural investigations of metal-oxide nanocrystals by powder X-ray diffraction: Colloidal tungsten oxide as a case of study. Chemphyschem 2016, 17, 699–709. [Google Scholar] [CrossRef] [PubMed]
- Migas, D.B.; Shaposhnikov, V.L.; Borisenko, V.E. Tungsten oxides. II. The metallic nature of Magnéli phases. J. Appl. Phys. 2010, 108, 093714. [Google Scholar] [CrossRef]
- Barabanenkov, Y.A.; Val’kovskii, M.D.; Zakharov, N.D.; Zibrov, I.P.; Popov, A.I.; Filonenko, V.P. Structure of tungsten oxide W O2.625 (W32 O84). Russ. J. Inorg. Chem. 1992, 37, 9–12. [Google Scholar]
- Viswanathan, K.; Brandt, K.; Salje, E. Crystal structure and charge carrier concentration of W18 O49. J. Solid State Chem. 1981, 36, 45–51. [Google Scholar] [CrossRef]
- Juhas, P.; Davis, T.; Farrow, C.L.; Billinge, S.J.L. PDFgetX3: A rapid and highly automatable program for processing powder diffraction data into total scattering pair distribution functions. J. Appl. Cryst. 2013, 46, 560–566. [Google Scholar] [CrossRef]
- Farrow, C.L.; Juhas, P.; Liu, J.W.; Bryndin, D.; Božin, E.S.; Bloch, J.; Proffen, Th.; Billinge, S.J.L. PDFfit2 and PDFgui: Computer programs for studying nanostructure in crystals. J. Phys. Condens. Matter 2007, 19, 335219. [Google Scholar] [CrossRef] [PubMed]
- Corricelli, M.; Depalo, N.; Fanizza, E.; Altamura, D.; Giannini, C.; Siliqi, D.; Di Mundo, R.; Palumbo, F.; Agostiano, A.; Striccoli, M.; et al. 2D Plasmonic Superlattice Based on Au Nanoparticles Self-Assembling onto a Functionalized Substrate. J. Phys. Chem. C 2014, 118, 7579–7590. [Google Scholar] [CrossRef]
- Altamura, D.; Holy, V.; Siliqi, D.; Lekshimi, I.C.; Nobile, C.; Maruccio, G.; Cozzoli, P.D.; Fan, L.; Gozzo, F.; Giannini, C. Exploiting GISAXS for the study of 3D ordered superlattice of self-assembled colloidal iron oxide nanocrystals. Cryst. Growth Des. 2012, 12, 5505–5512. [Google Scholar] [CrossRef]
- Ribic, P.R.; Margaritondo, G. Status and prospects of X-ray free-electron lasers (X-FELs): A simple presentation. J. Phys. D: Appl. Phys. 2012, 45, 213001. [Google Scholar] [CrossRef]
- De Caro, L.; Altamura, D.; Arciniegas, M.; Siliqi, D.; Kim, M.R.; Sibillano, T.; Manna, L.; Giannini, C. Ptychographic Imaging of Branched Colloidal Nanocrystals Embedded in Free-Standing Thick Polystyrene Films. Sci. Rep. 2016, 6, 19397. [Google Scholar] [CrossRef] [PubMed]
- Rodenburg, J.M.; Hurst, A.C.; Cullis, A.G.; Dobson, B.R.; Pfeiffer, F.; Bunk, O.; David, C.; Jefimovs, K.; Johnson, I. Hard-X-ray Lensless Imaging of Extended Objects. Phys. Rev. Lett. 2007, 98, 034801. [Google Scholar] [CrossRef] [PubMed]
- Thibault, P.; Dierolf, M.; Menzel, A.; Bunk, O.; David, C.; Pfeiffer, F. High-Resolution Scanning X-ray Diffraction Microscopy. Science 2008, 321, 379–382. [Google Scholar] [CrossRef] [PubMed]
- Dierolf, M.; Menzel, A.; Thibault, P.; Schneider, P.; Kewish, C.M.; Wepf, R.; Bunk, O.; Pfeiffer, F. Ptychographic X-ray computed tomography at the nanoscale. Nature 2010, 467, 436–439. [Google Scholar] [CrossRef] [PubMed]
- Fienup, J.R. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef] [PubMed]
- Fienup, J.R. Phase retrieval algorithms: A personal tour. Appl. Opt. 2013, 52, 45–56. [Google Scholar] [CrossRef] [PubMed]
- Gottstein, C.; Wu, G.; Wong, B.J.; Zasadzinski, J.A. Precise Quantification of Nanoparticle Internalization. ACS Nano 2013, 7, 4933–4945. [Google Scholar] [CrossRef] [PubMed]











| Crystal Lattice | Material | Space Group | a,b,c [Å] | Size [Å] | Size [Å] |
|---|---|---|---|---|---|
| Cubic | Cu-copper | F m−3 m | a = b = c = 3.623 | 159 [111] | 95 [200] |
| Monoclinic | CuO-tenorite | C 2/c | a = b = 4.685 c = 5.128 | 244 | 244 |
| Tetragonal | TiO2-anatase | I 41/a m d | a = b = 3.784 c = 9.508 | 162 [200] | 139 [004] |
| Tetragonal | TiO2-rutile | P 42/m n m | a = b = 4.597 c = 2.958 | 233 | 233 |
| Hexagonal | Ca5(PO4)3(OH)-hydroxyapatite | P 63/m | a = b = 9.465 c = 6.9095 | 210 [002] | 25 [110] |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giannini, C.; Ladisa, M.; Altamura, D.; Siliqi, D.; Sibillano, T.; De Caro, L. X-ray Diffraction: A Powerful Technique for the Multiple-Length-Scale Structural Analysis of Nanomaterials. Crystals 2016, 6, 87. https://doi.org/10.3390/cryst6080087
Giannini C, Ladisa M, Altamura D, Siliqi D, Sibillano T, De Caro L. X-ray Diffraction: A Powerful Technique for the Multiple-Length-Scale Structural Analysis of Nanomaterials. Crystals. 2016; 6(8):87. https://doi.org/10.3390/cryst6080087
Chicago/Turabian StyleGiannini, Cinzia, Massimo Ladisa, Davide Altamura, Dritan Siliqi, Teresa Sibillano, and Liberato De Caro. 2016. "X-ray Diffraction: A Powerful Technique for the Multiple-Length-Scale Structural Analysis of Nanomaterials" Crystals 6, no. 8: 87. https://doi.org/10.3390/cryst6080087
APA StyleGiannini, C., Ladisa, M., Altamura, D., Siliqi, D., Sibillano, T., & De Caro, L. (2016). X-ray Diffraction: A Powerful Technique for the Multiple-Length-Scale Structural Analysis of Nanomaterials. Crystals, 6(8), 87. https://doi.org/10.3390/cryst6080087