Role of Internal Radiation in Oxide Crystal Growth by Heat Exchanger Method
Abstract
:1. Introduction
2. Model Description
2.1. Modeling of Global Heat Transfer and Internal Radiation
2.2. Modeling of Thermal Stress
2.3. Boundary Conditions
3. Results and Discussion
3.1. Grid Independence
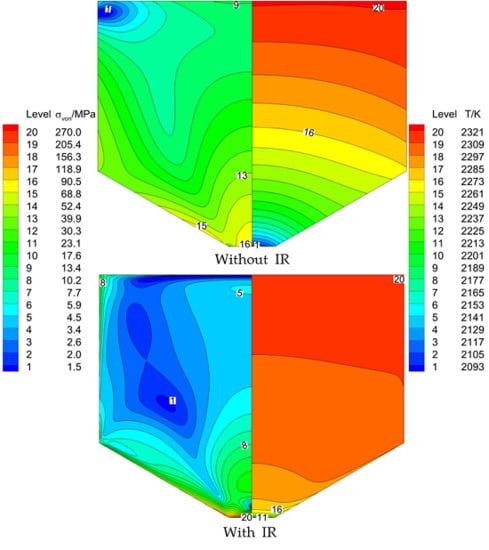
3.2. With and without Internal Radiation
3.3. Effect of Absorption Coefficient
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cockayne, B.; Chesswas, M.; Gasson, D.B. Facetting and optical perfection in Czochralski grown garnets and ruby. J. Mater. Sci. 1969, 4, 450–456. [Google Scholar] [CrossRef]
- Kvapil, Ji.; Kvapil, Jo.; Manek, B.; Perner, B.; Autrata, R.; Scuer, P. Czochralski growth of YAG:Ce in a reducing protective atmosphere. J. Cryst. Growth 1981, 52, 542–545. [Google Scholar] [CrossRef]
- Tsukada, T.; Kakinoki, K.; Hozawa, M.; Imaishi, N. Effect of internal radiation within crystal and melt on Czochralski crystal growth of oxide. Int. J. Heat Mass Transf. 1995, 38, 2707–2714. [Google Scholar] [CrossRef]
- Kobayashi, M.; Tsukada, T.; Hozawa, M. Effect of internal radiative heat transfer on transition of flow modes in Cz oxide melt. J. Cryst. Growth 2000, 208, 459–465. [Google Scholar] [CrossRef]
- Nunes, E.M.; Naraghi, M.H.N.; Zhang, H.; Prasad, V. A volume radiation heat transfer model for Czochralski crystal growth processes. J. Cryst. Growth 2002, 236, 596–608. [Google Scholar] [CrossRef]
- Yuferev, V.S.; Budenkova, O.N.; Vasiliev, M.G.; Rukolaine, S.A.; Shlegel, V.N.; Vasiliev, Y.V.; Zhmakin, A.I. Variations of solid-liquid interface in the BGO low thermal gradients Cz growth for diffuse and specular crystal side surface. J. Cryst. Growth 2003, 253, 383–397. [Google Scholar] [CrossRef]
- Hayashi, A.; Kobayashi, M.; Jing, C.J.; Tsukada, T.; Hozawa, M. Numerical simulation of the Czochralski growth process of oxide crystals with a relatively thin optical thickness. Int. J. Heat Mass Transf. 2004, 47, 5501–5509. [Google Scholar] [CrossRef]
- Banerjee, J.; Muralidhar, K. Role of internal radiation during Czochralski growth of YAG and Nd:YAG crystals. Int. J. Therm. Sci. 2006, 45, 151–167. [Google Scholar] [CrossRef]
- Tavakoli, M.H. Numerical study of heat transport and fluid flow during different stages of sapphire Czochralski crystal growth. J. Cryst. Growth 2008, 310, 3107–3112. [Google Scholar] [CrossRef]
- Fang, H.S.; Zhang, Q.J.; Tian, J.; Wang, S.; Ma, R.H. Study of internal radiation with solute inclusions during Czochralski sapphire crystal growth. Int. J. Heat Mass Transf. 2014, 79, 783–789. [Google Scholar] [CrossRef]
- Demina, S.E.; Kalaev, V.V. 3D unsteady computer modeling of industrial scale Ky and Cz sapphire crystal growth. J. Cryst. Growth 2011, 320, 23–27. [Google Scholar] [CrossRef]
- Demina, S.E.; Bystrova, E.N.; Lukanina, M.A.; Mamedov, V.M.; Yuferev, V.S.; Eskov, E.V.; Nikolenko, M.V.; Postolov, V.S.; Kalaev, V.V. Numerical analysis of sapphire crystal growth by the Kyropoulos technique. Opt. Mater. 2007, 30, 62–65. [Google Scholar] [CrossRef]
- Demina, S.E.; Bystrova, E.N.; Postolov, V.S.; Eskov, E.V.; Nikolenko, M.V.; Marshanin, D.A.; Yuferev, V.S.; Kalaev, V.V. Use of numerical simulation for growing high-quality sapphire crystals by the Kyropoulos method. J. Cryst. Growth 2008, 310, 1443–1447. [Google Scholar] [CrossRef]
- Lee, W.J.; Lee, Y.C.; Jo, H.H.; Park, Y.H. Effect of crucible geometry on melt convection and interface shape during Kyropoulos growth of sapphire single crystal. J. Cryst. Growth 2011, 324, 248–254. [Google Scholar] [CrossRef]
- Fang, H.S.; Jin, Z.L.; Zhang, M.J.; Zhang, Z.; Zhao, C.J. Role of internal radiation at the different growth stages of sapphire by Kyropoulos method. Int. J. Heat Mass Transf. 2013, 67, 967–973. [Google Scholar] [CrossRef]
- Lu, C.W.; Chen, J.C. Numerical computation of sapphire crystal growth using heat exchanger method. J. Cryst. Growth 2001, 225, 274–281. [Google Scholar] [CrossRef]
- Chen, J.C.; Lu, C.W. Influence of the crucible geometry on the shape of melt-crystal interface during growth of sapphire crystal using a heat exchanger method. J. Cryst. Growth 2004, 266, 239–245. [Google Scholar] [CrossRef]
- Vizman, D.; Nicoara, I.; Nicoara, D. On the factors affecting the isotherm shape during Bridgman growth of semi-transparent crystals. J. Cryst. Growth 1996, 169, 161–169. [Google Scholar] [CrossRef]
- Barvinschi, F.; Bunoiu, O.; Nicoara, I.; Nicoara, D.; Santailler, J.L.; Duffar, T. Factors affecting the isotherm shape of semi-transparent BaF2 crystals grown by Bridgman method. J. Cryst. Growth 2002, 237–239, 1762–1768. [Google Scholar] [CrossRef]
- Lan, C.W.; Tu, C.Y.; Lee, Y.F. Effects of internal radiation on heat flow and facet formation in Bridgman growth of YAG crystals. Int. J. Heat Mass Transf. 2003, 46, 1629–1640. [Google Scholar] [CrossRef]
- Backofen, R.; Bilz, T.; Ribalta, A.; Voigt, A. SPN-approximations of internal radiation in crystal growth of optical materials. J. Cryst. Growth 2004, 266, 264–270. [Google Scholar] [CrossRef]
- Stelian, C. Numerical modeling of radiative heat transfer in Bridgman solidification of semi-transparent BaF2 crystals. J. Cryst. Growth 2007, 306, 444–451. [Google Scholar] [CrossRef]
- Brandon, S.; Gazit, D.; Horowitz, A. Interface shapes and thermal fields during the gradient solidification method growth of sapphire single crystals. J. Cryst. Growth 1996, 167, 190–207. [Google Scholar] [CrossRef]
- Zhang, N.; Park, H.G.; Derby, J.J. Simulation of heat transfer and convection during sapphire crystal growth in a modified heat exchanger method. J. Cryst. Growth 2013, 367, 27–34. [Google Scholar] [CrossRef]
- Brandon, S.; Derby, J.J. Internal radiative transport in the vertical Bridgman growth of semitransparent crystals. J. Cryst. Growth 1991, 110, 481–500. [Google Scholar] [CrossRef]
- Brandon, S.; Derby, J.J. Heat transfer in vertical Bridgman growth of oxides: Effects of conduction, convection, and internal radiation. J. Cryst. Growth 1992, 121, 473–494. [Google Scholar] [CrossRef]
- Xiong, H.B.; Ma, Y.; Zheng, L.L. A modified HEM system for optical crystal growth with high melting temperature. J. Cryst. Growth 2007, 299, 404–412. [Google Scholar] [CrossRef]
- Ma, W.C.; Zhao, L.L.; Ding, G.Q.; Yang, Y.; Lv, T.Z.; Wu, M.; Liu, L.J. Numerical study of heat transfer during sapphire crystal growth by heat exchanger method. Int. J. Heat Mass Transf. 2014, 72, 452–460. [Google Scholar] [CrossRef]
- Wu, M.; Zhao, W.H.; Liu, L.J.; Yang, Y.; Ma, W.C.; Wang, Y. Effects of crucible cover on heat transfer during sapphire crystal growth by heat exchanger method. J. Cryst. Growth 2014, 404, 130–135. [Google Scholar] [CrossRef]
- Wu, M.; Liu, L.J.; Yang, Y.; Zhao, W.H.; Ma, W.C. Effect of crucible location on heat transfer in sapphire crystal growth by heat exchanger method. Heat Transf. Eng. 2015, 37, 332–340. [Google Scholar] [CrossRef]
- Miyagawa, C.; Kobayashi, T.; Taishi, T.; Hoshikawa, K. Development of the vertical Bridgman Technique for 6-inch diameter c-axis sapphire growth supported by numerical simulation. J. Cryst. Growth 2014, 402, 83–89. [Google Scholar] [CrossRef]
- Liu, L.J.; Kakimoto, K. Partly three-dimensional global modeling of a silicon Czochraski furnace. I. Principles, formulation and implementation of the model. Int. J. Heat Mass Transf. 2005, 48, 4481–4491. [Google Scholar] [CrossRef]
- Chai, J.C.; Lee, H.S.; Patankar, S.V. Finite volume method for radiation heat transfer. J. Thermophys. Heat Transf. 1994, 8, 419–425. [Google Scholar] [CrossRef]
- Chai, J.C.; Lee, H.S.; Patankar, S.V. Ray effect and false scattering in the discrete ordinates method. Numer. Heat Transf. B Fund. 1993, 24, 373–389. [Google Scholar] [CrossRef]
- Wu, M.; Liu, L.J. Effect of Angular Discretization on the Radiation Heat Transfer by Finite Volume Method. Science Paper Online, Article No. 201308-72. Available online: http://www.paper.edu.cn/releasepaper/content/201308-72 (accessed on 8 August 2013).
- Fainberg, J.; Leister, H.J. Finite volume multigrid solver for thermo-elastic stress analysis in anisotropic materials. Comput. Methods Appl. Mech. Eng. 1996, 137, 167–174. [Google Scholar] [CrossRef]









| Description | Value |
|---|---|
| Density(kg/m3): | |
| crystal | 3000 |
| tungsten | 19,350 |
| steel | 7600 |
| Thermal conductivity (W/(m·K)): | |
| crystal | 5.8 |
| tungsten | 174 |
| steel | 70 |
| helium | 0.067 + 3.2 × 10−5 × T − 4.0 × 10−8 × T2 |
| Heat capacity(J/(kgK)): | |
| crystal | 765 |
| tungsten | 130 |
| helium | 5200 |
| steel | 1000 |
| Dynamic viscosity (kg/(m·s)): | |
| helium | 5.58 × 10−5 |
| Emissivity: | |
| crystal | 0.9 |
| tungsten | 0.3 |
| steel | 0.2 |
| Other properties: | |
| thermal expansion of crystal (K−1) | 5.0 × 10−6 |
| absorption coefficient of crystal (m−1) | 0–1900 |
| refractive index of crystal | 1.78 |
| elastic modulus of crystal (GPa) | 430 |
| poison ratio of crystal | 0.28 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, W.; Liu, L. Role of Internal Radiation in Oxide Crystal Growth by Heat Exchanger Method. Crystals 2017, 7, 18. https://doi.org/10.3390/cryst7010018
Ma W, Liu L. Role of Internal Radiation in Oxide Crystal Growth by Heat Exchanger Method. Crystals. 2017; 7(1):18. https://doi.org/10.3390/cryst7010018
Chicago/Turabian StyleMa, Wencheng, and Lijun Liu. 2017. "Role of Internal Radiation in Oxide Crystal Growth by Heat Exchanger Method" Crystals 7, no. 1: 18. https://doi.org/10.3390/cryst7010018
APA StyleMa, W., & Liu, L. (2017). Role of Internal Radiation in Oxide Crystal Growth by Heat Exchanger Method. Crystals, 7(1), 18. https://doi.org/10.3390/cryst7010018