3. Thermodynamics of Polymer Crystallization
In the previous section, we discussed the chain trajectory in polymer crystals, the folded chain model. In this section, we will mainly focus on the thermodynamic aspects of polymer lamellar crystals. Thermodynamics is simple but powerful. On the one hand, thermodynamics is a phenomenological theory directly connecting microscopic structure to macroscopic parameters, e.g., the variation of lamellar thickness with supercooling. Such relations allow us to compare theoretical predictions with experiments in an explicit manner. On the other hand, a set of fundamental principles established by thermodynamics will rule out any theory that violates thermodynamic consideration. Therefore, thermodynamic aspects of lamellar crystals should be taken into account first.
According to the classical thermodynamics, the total free energy change relevant to formation of a crystal from amorphous phase can be expressed as
The first, second, and third term on right hand side (RHS) represent the total lateral surface energy, the fold surface energy, and the bulk free energy change, respectively. Alat, A, and l correspond to the lateral surface area, the folded surface area, and the lamellar thickness, respectively. The basic assumption of Equation (1) is that the surface energy per area and the bulk energy per volume do not vary with the crystal size. Since the folded surface area is much larger than that of lateral one for sufficiently large crystals, namely A>>Alat, the first term on RHS can be ignored.
The bulk free energy change is defined as
where ∆
H(
T) and ∆
S(
T) are enthalpy and entropy changes at temperature
T, respectively.
Obviously, Δ
G = 0 specifies the minimal lamellar thickness
lmin for an infinitely large lamellar crystal:
Note that the minimal lamellar thickness obtained here is entirely based on thermodynamic considerations, and the total free energy decreases with the increase in lamellar thickness, which implies that extended-chain crystals correspond to the lowest free energy state. However, any lamella with a thickness greater than lmin will also be thermodynamically accessible, namely, they could be in metastable states. If a large free energy barrier needs to be overcome in the formation of a final equilibrium state, metastable states with a finite lamellar thickness may occur.
The actual crystal thickness is always larger than
lmin to assure crystal growth, and can be expressed as
If δl/lmin is much smaller than unity, the lamellar thickness approximately equals to lmin, then we can replace l with lmin. Hence, correct estimations of ∆F and σe in Equation (4) will be crucial.
As a first-order approximation [
43], we assume that both ∆
H and ∆
S are weakly dependent on temperature near the equilibrium point, namely, ∆
H and ∆
S are almost constant in the vicinity of
Tm and can be replaced by ∆
H[
Tm(∞)] and ∆
S[
Tm(∞)]:
Immediately, we obtain a linear relation between ∆F and ∆T, which indicates that the driving force for crystallization will linearly increase with supercooling.
However, we must point out that this approximation is valid only when the supercooling is sufficient small. Once the system is in large supercooling, and once ∆H and ∆S are no longer constant and remarkably change with temperature, the heat capacity contribution must be considered.
However, it is difficult in presenting the correct form of heat capacity in terms of temperature, and such kind of formula has been argued for a long time [
44,
45].
An alternative approach may be employed by introducing an empirical correction function
K(
T), which is directly multiplied on ∆
F, leading to
K(
T) is usually called the reduced Gibbs free energy change. Historically,
K(
T) has been endowed with various forms by many researchers. However, this scheme also encounters difficulties; for example, it was found that there was no universal formula of
K(
T) to match all polymer systems [
46,
47,
48]. However, Schawe [
49] recently proposed a new approach and concluded that his method might be generally valid for all polymers in the temperature range between the equilibrium melting temperature and the glass transition temperature.
It is necessary to point out that, in traditional calculations of ∆
F, heat capacity correction was seldom taken into account. So far, most treatments still employ the simplest linear extrapolation approximation form for the temperature dependence of ∆
F. The well-known Gibbs–Thomson relation for crystal size dependence is based on this simplified model as well [
50]. However, for simplicity, in what follows, we ignore such corrections, and resort to the simplified expression of ∆
F. Even so, the calculation of ∆
F still has other potential problems.
Substituting the expression of Δ
F into the formula of lamella thickness,
lmin could be obtained
It can be shown that the critical lamellar thickness is inversely proportional to supercooling, which is in accordance with experimental results.
However, it must be noted that it could be a misunderstanding to regard Δ
F as a bulk free energy change within polymer crystals in that the crystals are not infinitely large [
51]. Even though no folding surfaces exist, all free ending groups will locate at crystal surfaces. Therefore, free ending surface effects cannot be ignored even for extended-chain crystals [
52]. However, Hoffman [
53] ignored the free ending effects and regarded the above equation as the definition of bulk free energy change and assumed that
σe had the same interpretation as that of the infinite chain length, namely, the surface tension of the fold surface.
This issue was firstly recognized by Kovacs et al. [
51], who argued that the aforementioned expression of ∆
F must subtract an appropriate term relevant to free ending effect, which corresponds to the entropy of localization due to the pairing of chain ends and becomes important in the case of closely stacked lamellar crystals. This amounts to −
kBln(
CN) per molecule, where k
B is the Boltzmann constant, and
C is a constant related to the flexibility of the chains in the melt [
54].
The origin of this expression stems from the fact that each polymer chain has two ends, which provides an excess of degree of freedom. For a polymer chain with
N monomers, the portion of chain ends equals 2/
N. According to Boltzmann’s entropy formula
S =
kBln
W, the packing entropy should be proportional to
kBln(2/
N), which is exactly the same form as −
kBln(
CN) apart from a constant difference. Hence, if we consider the free ending correction, we will have
where υ represents the volume of one statistical unit since ∆F is defined as the free energy change per unit volume. Recently, Crist [
55] also proposed that the entropy resulting from chain folding and cilium increases the effective surface energy, making crystals thicker than the previous estimation. In addition, another consequence of the surface entropy is that the equilibrium amorphous fraction increases with crystallization temperature.
So far, we have considered the finite size effect based on thermodynamic arguments. However, recent experiments on semicrystalline polymers with ultrafast heating rates have inspired new insights into how lamellar crystals rearrange themselves [
56,
57]. In particular, instrument developments, such as ultrafast chip calorimetry, have allowed experiments with extremely fast heating rates of up to 100,000 K/s, much faster than those attainable in traditional calorimetric measurements with a typical heating rate of about 10 K/min. Under this conventionally relative slow heating rate, the annealing process simultaneously takes place, which leads to the spontaneous lamellar thickening. It is commonly believed that, under a relatively high heating rate such as 1000 K/s, the annealing process can be effectively prohibited due to the sluggish motion of long-chain polymers [
58]. However, recent experiments [
56] have shown that, even at a heating rate of 100,000 K/s, the annealing process can still be probed, which indicated that there may be a quite rapid process when heating polymer crystals, and the difference between the melting temperatures measured at extremely fast heating rates and those observed during normal calorimetric measurements at slower heating rates were caused by changes in metastability during crystal heating [
59].
It can be seen that there are many issues in traditional arguments of polymer crystals in the context of thermodynamics as well as the kinetic process. The latest progress from experiments and simulations presents increasing challenges to the commonly used concepts [
60,
61,
62]. Therefore, a careful interpretation of experimental data and an awareness of the defects of various theories are crucial.
4. Secondary Nucleation Theories
So far, people have realized that the vast majority of polymer crystals are in metastable states with folded chain structures. It is now widely accepted that polymer crystallization process is determined by kinetics rather than thermodynamics; thus, correspondingly, the so-called “kinetic theory” over the equilibrium theory will be responsible for the description of polymer crystallization. Typical kinetic theory usually includes two parts: one corresponds to the “driving force,” and the other is relevant to some kind of “free energy barrier.” These two terms compete with each other and result in an optimal growth rate associated with specific lamellar thickness.
That is to say, according to kinetic theory, lamellae with any thickness larger than
lmin can be formed; however, lamellae with various thicknesses will lead to different growth rates, and the experimental observation corresponds to the fastest growth rate, which is the meaning of
kinetic theory. The “driving force” stems from the free energy difference between the crystalline and amorphous phases, which would be the same for all kinetic theories, and the origin of “free energy barrier” differentiates various kinds of kinetic theories. In fact, polymer crystallization is a very complicated process, involving diffusion, adsorption, desorption, entanglement, exclusion of defects, and so on. Any factor that slows down the growth of crystals could be regarded as some type of “barrier” [
63]. Due to the complex nature of polymer crystallization, it is difficult to specify a certain element acting as the universal “barrier.” Instead, under certain conditions, a rate-limiting step will be phenomenologically regarded as the “barrier.”
Early studies mainly focused on the theories of secondary nucleation, which is defined as the nucleation and growth process on the well-defined crystal surfaces. Therefore, secondary nucleation is frequently called the surface nucleation process. However, in recent decades, thanks to advances in experimental techniques, particularly the application of scattering approaches in polymer science, a deeper understanding of early stages of crystallization has been gained. Here, we still follow the course of history, and divide nucleation theories into secondary nucleation (
Section 4) and primary nucleation (
Section 5). Despite some kind of artificial division, we hope that a comparison of diverse approaches relevant to the same issue will assist us in clarifying the differences and similarities between various theories, and in appreciating why seemingly quite distinct assumptions eventually yield similar predictions.
4.1. The Hoffman–Lauritzen Theory
Up to now, the most successful and widely accepted theory was proposed by Hoffman and Lauritzen [
5], now known as Hoffman–Lauritzen (HL) theory or the Lauritzen–Hoffman (LH) theory. One of the advantages of the HL theory is that it provides a simple analytical form to connect microscopic parameters with macroscopic quantities. However, to be presented in a simple formalism, it is necessary to ignore numerous complicated details, namely, to sacrifice the personality of each molecule and hold their common attribute, inevitably resulting in a mean-field-type description. Such simplifications were considered to be oversimplified by many researchers, and the HL theory has been constantly challenged by experimentalists and theorists; correspondingly, the HL theory itself continuously underwent a series of extensions and modifications. Nonetheless, the HL theory has become a “standard model” of polymer crystallization, though some parameters are phenomenological and some assumptions are oversimplified.
In the following, we will outline the basic assumptions of the HL theory, as well as its physical implications and consequences. In addition, we will compare its predictions with experiments and point out the successful and frustrated parts. Finally, we will present brief comments on the HL theory.
The HL theory assumes that the critical nucleus is a single stem created by random fluctuation, longer than the minimum lamellar thickness
lmin. Other stems further deposit on the crystal front to complete the growth process, which results in lateral spreading and the formation of a new layer, and then wait for the next nucleation event, which is illustrated in
Figure 3.
Here, we need to further analyze its assumptions. These simplified assumptions were supplemented or revised later, leading to a series of corrections and modifications by several authors.
(1) The critical nucleus is considered as a single stem. Obviously, this is a coarse-graining description and undoubtedly leads to a mean field theory. In the light of the traditional nucleation process of non-polymeric substances, small molecules continue to fluctuate in and out of an embryo [
64,
65], up to the formation of the critical nuclei with certain characteristic dimension and then stabilizes, indicating that nucleation is a sequential process per se. The nucleation process of polymers should be analogous to that of small molecules. Units (or segments) have experienced a course of intricate steps and ultimately form a stable stem with a dimension larger than the minimum lamellar thickness. Compared with the coarse-graining model involved in the HL theory, the above description in terms of a sequential process is generally referred to as the “fine grained model.” Frank and Tosi [
66] proved that, when a detailed balance was satisfied, or roughly speaking, when the system was in equilibrium, these two approaches were equivalent, leading to the same results.
However, Frank and Tosi assumed that units could only fluctuate on and off along the direction of the lamellar thickness, and chain folding was inaccessible before the cumulative length of units reached the lamellar thickness, as illustrated in
Figure 4.
This hypothesis was subsequently modified by Point [
67,
68], who argued that, at each substep, chain folding had a certain probability of occurring (see
Figure 5). Such modifications considerably altered the final formalism, and the resulting consequences were significant: it effectively excluded the serious problem of “
δl-catastrophe.” We will return to this point later.
(2) After the initial deposition of the nucleus onto the crystal surface, the remaining polymer chain will be sequentially adsorbed to the front with the same length as the original one. In principle, the stem length may be subject to a certain degree of fluctuation (
δl) due to thermal agitation; therefore, a natural question arises: To what extent will the fluctuation be? If the fluctuation effect is weak, it can be regarded as some kind of perturbation. As a zero-order approximation, it can even be neglected; thus, we return to Hoffman’s treatment. However, if the influence of fluctuation cannot be ignored, the HL theory may fail. Here, we present an intuitive estimation, and the detailed quantitative computation can be found in relevant papers [
8,
25,
69].
According to the fluctuation–dissipation theorem [
70], the fluctuation of the lamellar thickness is associated with corresponding dissipation in that they share the same driving force, namely, the thermal random force
kBT, where
kB is the Boltzmann constant, and T is the absolute temperature. The natural consequence of fluctuation is to create more lateral surfaces; therefore, dissipation is related to the lateral surface energy
σ. Analogous to classical Einstein’s relation, we immediately have
or
where
b is the width of the stem (see
Figure 3 for more details). The physical consideration underlies that, since the driving force relevant to fluctuation is of order
kBT, the dissipation energy resulting from the same origin must be of the same order of magnitude.
Although the lamellar thickness is allowed certain extent of fluctuation, here we merely deal with lamellae with a constant thickness since the consideration of thickness fluctuation does not introduce much difference. Interested readers can refer to the relevant literature [
66,
71].
(3) In addition, the HL theory also implicitly assumed that, once nuclei formed, the whole chain must be consumed for lateral growth. Until a polymer chain was completely depleted, another chain could be incorporated for further growth. This is a natural consequence of the tightly folding model. The description may be true in a dilute solution; however, with an increase in concentration, or even in the melt, other chains may inevitably be embodied before the initial chain is entirely consumed. The resulting formation of the “cilium” structure originally proposed by Dimarzio [
72] can bring in at least two distinct effects: (a) Cilia facilitate secondary nucleation in that the cilium is close to the crystal surface layer, which is much easier to deposit on the next crystal layer compared with a new molecular chain; (b) cilia improve the mechanical properties of materials. Once a cilium is long enough, it may transverse various lamellae, resulting in tie molecules. This is a kind of recurrence of Flory’s switchboard model, as well as one of the starting points of subsequent theories such as Hoffman’s variable cluster theory [
73] and Hu’s intramolecular nucleation theory [
41].
Furthermore, Dimarzio was able to estimate the fraction of ciliated material generated with respect to molecular weight; thereafter, a series of generalizations was made [
71,
74]. However, in the original treatment of the HL theory, these possibilities are ignored.
(4) Smooth surface nucleation. This may be the subtlest, yet the most critical assumption in the HL theory. A smooth surface means that the preexisting surface is atomically smooth, which implies that each step of deposition will create new surfaces. A smooth surface is almost planar with few “steps“ or “vacancies”; however, at elevated temperatures, a smooth surface may become rough.
The transition between these two profiles is known as the roughening transition. This phenomenon was first conjectured by Burton, Cabrera, and Frank [
75]. This transition is expected to appear when either the step free energy is of the order of
kBT or the height correlation length becomes negligibly small [
76,
77]. The transition temperature
TR can be considered as the temperature at which the entropic gain from a fluctuation becomes greater than its associated loss in energy. Therefore, the smooth surface hypothesis largely determines HL to be an “enthalpy barrier” model, which is in sharp contrast to the later developed “entropy barrier” model.
From the aforementioned arguments, it can be seen that the elementary process involved in the HL theory is rather simple. It only consists of two steps: one is to create a new nucleus; the other is relevant to lateral growth. Consequently, two phenomenological parameters can be defined to completely characterize the polymer crystallization process within the framework of the HL model. Correspondingly, one is nucleation rate i, which is defined as the net deposition rate on the surface per unit substrate length. The other is spreading rate g, which is expressed as the difference between the rate of the arrival and departure of stems at the crystal surface.
However, deeper insight into these two quantities can be intuitively gained by considering their asymptotic behaviors before introducing the specific expressions of i and g, which leads to the so-called “regime phenomenon.”
(1)
I <<
g. This corresponds to Regime I [
78], usually at high temperatures, where the nucleation rate is much smaller than the lateral spreading rate. Once a nucleation event occurs, subsequent lateral growth will rapidly overspread a layer, and wait for the next nucleation event. Therefore, the crystal growth rate is controlled by the nucleation rate. Since
i is defined as the nucleation rate per unit substrate length and, hence, if the crystal size is
L, the nucleation rate is
iL, and the crystal growth rate is
ibL, then
However, an immediate consequence derived from this equation is that
GI is proportional to
L, namely, crystal growth rate is linearly dependent on the crystal width, implying that wider crystals have faster growth rates. This is inconsistent with experimental results that the crystal growth rate is almost constant, independent of the crystal size; therefore,
L needs to be redefined. It is now generally argued that
L is an “effective length” much smaller than the width of the crystal growth face, and
L is usually represented by
Lp, where the subscript
p means “persistence” and
Lp is called the “persistence length” [
79,
80]. The introduction of persistence length effectively limits the spacing of continuous crystal growth. Therefore, the above equation may be modified as
However, the introduction of Lp may be one of the most serious issues in the HL theory and leads to long-term controversy. In what follows, we will discuss this problem.
(2)
I >>
g. This case is usually called Regime III [
73,
81], in which nucleation rate is much faster than the lateral spreading rate, corresponding to low temperatures. It is believed that, in this case, nucleation events are so frequent that the averaged spacing between two adjacent nuclei again become a constant, and the lateral spreading rate is thus physically irrelevant. Thus, the system will show similar behaviors as in Regime I.
Instead,
Lp needs to be considered as the average distance between two adjacent nuclei, which is expected to be two to three lattice spacing.
(3)
i approximately equals to
g. This condition is referred to as Regime II, corresponding to a moderate temperature range. In this case, the nucleation rate and lateral spreading rate are comparable, leading to the competition between these two factors. The resulting expression involves the same statistical weight of
i and
g [
71].
One of the remarkable features of the regime phenomenon is that it only depends on the relative values of
i and
g; therefore, if we can effectively tune the magnitudes of
i and
g, for instance, by the crosslinking method [
82], regime transitions could be observed at the same temperature.
As mentioned earlier, the essential part of the HL theory is to present the analytic expressions of
i and
g, which leads to explicit relations of macroscopic quantities in terms of microscopic parameters. Thus, we can predict the lamellar thickness and crystal growth kinetics from a microscopic perspective. Here, we briefly present the basic logic flow, and the detailed derivations can be referred to the original work [
5,
46,
69,
81,
83].
In the LH model a nucleus is formed and subsequently spreads by the addition and removal of sequential stems, and the probabilities of addition and removal are related by the detailed balance in steady state approximation.
For the nucleation process, according to the original assumption, the first step of deposition does not create any folding surface, and only lateral surfaces are generated; for the lateral spreading process, since lateral surfaces are no longer created, only folded surfaces are generated. Therefore, the free energies relevant to each process are well specified.
However, such expressions only provide the ratio between different microscopic parameters. In order to derive the expressions of i and g, the absolute values of the probabilities of addition and removal must be given. Therefore, the total free energy must be partitioned to each microscopic quantity, which is known as the “apportioning problem.”
Hoffman proposed the apportioning principle based on the fact that the free energy cost due to the surfaces acts as a barrier to overcome in order to lay down a stem, and it should be embraced in the forward rate constants, namely, the probabilities of adding a stem. However, a certain extent of bulk free energy will be gained during the deposition process and therefore reduces this barrier; as a result, the actual amount will be determined by the factor ψ.
Having the specific expressions of microscopic parameters, deriving the macroscopic quantities, such as the lamellar thickness and the crystal growth rates in various regimes, is algebraically straightforward. Here, we simply present some main results
(1) The averaged lamellar thickness:
where
Obviously, δl is almost the same form (except for some prefactors) as our previous intuitive guess in the light of fluctuation–dissipation theorem.
Notice that, for small ∆F, δl is approximately constant and the main temperature dependence of <l>av is given by 2σe/∆F. Using the linear relationship between ∆F and ∆T, it can be immediately found that <l>av is inversely proportional to ∆T as observed experimentally.
(2) Fluctuation of lamellar thickness:
(3) Growth rates in various regimes:
where
β is the kinetic prefactor. From the above results, we can find that, basically speaking, the HL theory can quantitatively or semi-quantitatively reproduce the main experimental observations, which demonstrates the success of the HL theory since, under such simple assumptions, it can correctly predict most experimental results. Though the theory inevitably has many deficiencies, here we only point out several of them. For more details, readers can refer to [
8,
67,
84,
85,
86].
4.1.1. δl Catastrophe
From Equation (19), it is easy to see that once the denominator (1-a∆
Fψ/2
σ) equals to zero,
δl will diverge, which indicates that crystallization at this specific temperature has no energy barrier and may generate crystals with infinite thickness. This has never been observed in experiments. Therefore, the only way of eliminating the
δl catastrophe is to set
ψ as 0; however, this manipulation completely violates the original intention of the introduction of
ψ. In addition, it will lead to an unphysical result: if stems are adsorbed on the crystal surface, all surface energy must be overcome first before any gain of bulk free energy. Subsequently, Frank and Tosi [
66], as well as Lauritzen and Passaglia [
78], developed corresponding theories that considered fluctuations. However, any theory based on the framework of HL-type with non-zero
ψ will eventually lead to
δl catastrophe. After Point proposed the multi-path approach, this problem could be fairly well solved.
Point [
67] first assumed that, in each step, a unit or a segment rather than a complete stem would deposit on the crystal surface, which is similar to fine-grained model of Frank and Tosi [
66]. However, in Point’s approach, chain folding can occur at any stage, namely, when each unit deposits on the crystal surface, in addition to the longitudinal growth, it can also have some probability to fold (see
Figure 5); in the Frank–Tosi treatment (see
Figure 4), it is assumed that “the segments which join the stem are allowed to fluctuate forwards and backwards, but only when they have reached the lamellar thickness are they allowed to fold” [
66]. Therefore, in Point’s model, even though the cumulative length has not reached the assigned lamellar thickness, a folding event occurs, so the subsequent growth process along the thickness is terminated. Further thickness growth must rely on the removal of unfavorable folding configurations; therefore, the unfavorable configuration corresponds to some kind of “pinning point,” and the removal of unfavorable configurations (pinning points) will cost time, which is equivalent to slowing down the crystal growth rate. Hence, it can be regarded as some type of “nucleation barrier.”
The introduction of unfavorable configurations is essentially some kind of “entropy effect,” which is related to the number of configurations, namely, corresponds to entropy degeneracy. This concept was subsequently extended by Sadler and Gilmer [
85] and now known as the Sadler–Gilmer (SG) model, which will be discussed in detail in the following section.
Once the concept of entropy barrier is introduced, the
δl catastrophe is completely avoided. Intuitively, it is easy to imagine that, when the lamellar thickness increases, the probability of the formation of unfavorable configurations becomes higher before reaching the assigned lamellar thickness. Generally speaking, it is not possible to grow lamellae with infinite thickness. Strict mathematical treatment can be found in [
87].
4.1.2. Curved Single Crystals
The HL theory was originally designed for facetted single crystals that have clear crystallographic surfaces; however, it was experimentally found later that, at elevated temperatures, crystals with curved edges can be observed in both solution and melt [
88,
89]. Obviously, this phenomenon is inconsistent with the original prediction of the HL theory. In the HL theory, high temperatures correspond to Regime I, which is controlled by the nucleation process; namely, once the first stem deposits on the preexisting surface, the subsequent covering rate is rather rapid and a resulting regular shape crystal can be obtained, which is, of course, in contrast to experimental results.
To reconcile the inconsistence between the HL theory and experimental observations, Hoffman and Miller [
90] modified the HL theory. They first noted the work of Patel and Farmer [
91], who studied the energetics of attaching a stem to (110) and (100) faces of polyethylene (PE) and found that stems are energetically favorable when crystallized on (100) surfaces, while the mobility is much higher when crystallized on (110) surfaces, leading to a higher lateral spreading rate. The slight difference results in the so-called “lattice strain,” which occurs due to the “bulkiness” of the fold along one growth face, and the interior of the crystal may expand. The resulting volume strain is translated into a strain surface free energy. By introducing the concept of a lattice strain, Hoffman and Miller can explain the curved edges of single crystals; however, Point [
92] soon proved that this treatment leads to another kind of
δl catastrophe. Therefore, it might be difficult to interpret curved edges based on the HL theory.
4.1.3. Lp Size Problem
The introduction of
Lp, as mentioned previously, is to take into account the fact that the crystal growth rate is irrelevant to the crystal size; therefore, the HL theory is only valid in a certain range of length scale, referred to as persistence length
Lp. The original estimation of
Lp in the HL theory was about a few microns; however, by means of the isochronous decoration method, Point [
79] subsequently proved that the
Lp value should be much lower than that predicted by the HL theory and concluded that the
Lp value cannot exceed 1 micron. Later, Hoffman and Miller further modified
Lp to a few hundred nanometers by comparison with an X-ray diffraction experiment [
93]. Until recently, using the dark field TEM technique, Lotz et al. [
94] directly probed this size and showed that it was rather close to the prediction of Hoffman and Miller.
It can be readily seen that the development of the HL theory is accompanied by adjusting parameters to be consistent with experimental results. On the one hand, the HL theory is quite general and flexible to accommodate a series of modifications and extensions; on the other hand, the HL theory actually omits some microscopic details of the nucleation process.
4.1.4. Phenomenon of Minimum Growth Rate
An integer folded phenomenon can usually be observed in the crystallization of n-alkanes [
95] and low molecular weight PEO [
96,
97,
98], which is probably because integer fold can exclude all end defects out of bulk crystals, and thereby reduce the free energy. In a certain temperature range, two adjacent growth modes, for instance, an extended chain and a once-folded chain, can coexist, since they have approximately the same growth rate. Within this temperature range, a minimal growth rate can often be observed. Taking n-alkanes as an example, early studies [
95,
99] and subsequent, more sophisticated experiments [
100,
101] found that, in a proper temperature window, a minimum growth rate would be observed. This unexpected result cannot be explained by the HL theory.
One possible mechanism originates from the “entropy effect.” We can imagine that, if the chain has been grown in an extended chain manner, when a specific temperature is chosen, the growth rates of the “extended chain” and the “once-folded chain” are comparable. At this temperature, it is possible to deposit a once-folded chain on an extended-chain crystal surface. Such a poisoning point will stop further crystal growth unless either of the two following conditions is satisfied: either the polymer chain undergoes conformation transition and transforms itself into the extended chain, or the unfavorable folded chain configuration is removed. Both steps will cost additional time, resulting in a minimal growth rate. Accordingly, this point is referred to as the “poisoning point” [
99], and this phenomenon is called the “self-poisoning phenomenon.” Since the origin of poisoning points corresponds to the deposition of unfavorable configurations, it is actually related to a kind of entropy effect. Hoffman [
102] modified his theory by introducing the entropy contribution in lateral surface free energy, namely, a transient layer of “kinetic ciliation”. Later, the characteristic ratio C
∞ was also taken into account [
103], and the rate minimum phenomenon was successfully reproduced.
From previous analysis, it is not difficult to see that the HL theory succeeds in many aspects and does not work in some facets. Nevertheless, the transparent assumptions as well as concise analytical form still make the HL theory the most widely accepted model. Knowing “how to approximate” rather than “how to be precise” resides in any good physical theory. From this viewpoint, the HL theory is extremely successful.
4.2. The Sadler–Gilmer Model
Having discussed the HL theory and its modifications, in what follows, we will present the Sadler–Gilmer (SG) model. The two approaches are distinctly different: the HL theory corresponds to the “enthalpic barrier,” while the SG model is relevant to the “entropic barrier.” Despite the fundamental difference, both of them lead to similar predictions of lamellar thickness as well as crystal growth kinetics.
The HL theory assumes that crystallization occurs on a “smooth surface,” namely, the crystal surface is smooth at the atomic scale. Thus, the nucleation barrier originates from the formation of new surfaces by the deposition of stems, leading to an increase in surface free energy. However, as mentioned before, when temperatures are sufficiently high (T > TR), crystal surfaces may be rough at the atomic level, including many “steps” or “vacancies.” Therefore, when new stems deposit on the surface, no more surface areas are created; therefore, it seems that no traditional nucleation barrier exists. However, polymer crystallization at elevated temperatures also shows a tendency similar to that at lower temperatures, indicating some kind of “nucleation” process. In order to explain the experimental observations, the concept of an entropy barrier was introduced.
The earliest exploration of this new mechanism can be traced back to Binsbergen [
104]; subsequently, Point proposed a similar idea, namely, the multi-path approach, and the essence of his idea is to introduce conformation entropy degeneracy, that is, to incorporate a wider range of choices available to the chain molecule during its attachment to the growth front. Therefore, an entropy part was added to the traditional “nucleation barrier.” In 1983, Sadler and Gilmer [
105] took this idea to extremes and argued that the nucleation barrier is completely an “entropy barrier” without enthalpic contribution. Meanwhile, they proposed that the regime transition from I to II corresponded to the transition from rough surface nucleation to smooth surface nucleation [
85,
105,
106].
The mechanism of the “entropy barrier” in the SG model is similar to that of Point’s approach. Due to chain connectivity, if one segment adopts some kind of wrong configuration, the subsequent deposition of stems will be blocked, and the resulting pinning point hinders further chain crystallization; therefore, the “wrong” conformations must be removed to keep the crystallization process continuing.
Obviously, this is different from the traditional nucleation theory since the concept of “critical nuclei” does not exist. However, under the generalized nucleation concept [
63], any step limiting crystal growth can be regarded as some type of “nucleation barrier.” In this general sense, the SG model may also be considered as a type of “nucleation theory.” Now, we can employ a unified viewpoint to examine all secondary nucleation theories.
In the SG theory, on the one hand, the driving force is still the free energy difference between the crystalline phase and the liquid phase, which is proportional to the thickness of the lamellar thickness. On the other hand, the barrier stems from the occurrence of “wrong configurations”; the thicker the lamella is, the higher the probability of making mistakes will be. Therefore, the barrier is positively correlated with l; hence, the competition of two factors leads to an optimal lamellar thickness; therefore, the SG model is also kinetic in nature. From this point of view, this framework is quite analogous to that of the HL theory, it is thus not surprising that the SG model will lead to predictions similar to those of the HL theory.
However, the SG theory is not an analytical theory, and the relevant theoretical predictions can only be realized by computer simulation. The lack of analytic treatment lies in that the SG model involves conformational statistics, which corresponds to the arrangement of segments on the crystal surface. Considering the enormous number of chain statistics, it will be hard for analytic methods to deal with the conformational degeneracy. Here, we will make some comments on the SG theory.
(1) The significance of the SG theory, in the authors’ opinion, is to provide another way of understanding the origin of nucleation barrier, though the conclusions derived from the SG model are frequently qualitative. According to the traditional HL theory, the nucleation barrier is enthalpic in nature. The SG model, however, points out another interpretation that the barrier can also originate from entropic contribution. Based on the “entropic barrier,” the same conclusions as in the HL theory can also be derived. In fact, this accordance originates from a plain idea: Since the free energy barrier includes two parts (∆
G* = ∆
H* −
T∆
S*), consideration either from the enthalpic or the entropic aspect will lead to some kind of free energy barrier. However, any concentration merely on enthalpy or entropy is insufficient. Therefore, SG might be regarded as a complementary rather than contrary approach in light of the HL theory. Comprehensive considerations of both enthalpy and entropy contribution will eventually lead to a deeper understanding of the polymer crystallization process [
63].
(2) Strictly speaking, the SG model was constructed with reference to small molecules. In small molecular crystals, Kossel-type crystals are taken into account, i.e., the nearest neighboring interactions are considered, and molecular adsorption or desorption can occur in any position on the crystal surface [
76]. However, a direct application to the polymer system will result in many problems. For example, since a polymer chain is connected by chemical bonds, a strong correlation along the chain direction exists, and the units within one chain cannot appear in any position on crystal surfaces. Therefore, in the SG model, the connectivity of long-chain molecules has not been fully considered, and the SG model is more appropriate for a short-chain system. Recently, one of the authors [
107] attempted to generalize the SG model to high polymers through the introduction of long-range correlations. Interested readers can refer to the original literature.
(3) The SG model was originally proposed based on two experimental facts: the curved edges at high temperatures and the rate minimum phenomenon. Both of these facts cannot be explained by the traditional HL theory, which promoted Sadler and Gilmer for the so-called “rough surface nucleation.” However, both of these two points are not necessarily attributed to a rough surface, and this has been a point of contention for a long time.
(a) Firstly, curved edges cannot always be seen at high temperatures. For instance, during the growth of PE crystals, curved lamellar growth only occurs on the (200) surface and does not show up at the rapid grown (110) surface; therefore, it seems arbitrary to consider rough surface crystallization as a general explanation. In addition, the strict definition of TR is associated with the thermodynamic limit, while the polymer crystals are usually in metastable folded states; hence, whether such a transition exists will be questionable. At least for metastable lamellar crystals, there may no longer be a sharp transition.
Moreover, in addition to the “lattice strain” proposed by Hoffman and the “rough surface” introduced by Sadler, other explanations also exist. For example, Toda [
89] attributed the curved edges to the influence of impurities. Furthermore, the solvent effects, the segregation of short-chain molecules, and the lattice mismatching are all likely to result in curved edges. Hence, surface roughening cannot necessarily be responsible for curved edges; on the contrary, a rough surface only serves as a possible explanation.
(b) On the other hand, considering the rate minimal phenomenon, Sadler argued that it was the pinning points that prevented the subsequent crystal growth. Later, Ungar and Keller [
99] generalized this idea, and the so-called “self-poisoning” mechanism was introduced. Recent experiments and simulations, however, preferred the interpretation of the occurrence of a self-poisoning phenomenon from the perspective of the driving force rather than the energy barrier [
108].
Based on the above arguments, it is better to consider the SG theory as an alternative rather than an inevitable approach. However, the unfortunate leave of David Sadler in 1989 terminated the further development of the SG model, which is far from satisfaction to everyone.
Previously, we mainly focus on two representative models: the HL and SG models, based on the enthalpic and the entropic barrier, respectively. In the following, we will further introduce other secondary nucleation theories. Compared to the HL theory, most of them remain in a conceptual level; therefore, we will concentrate on the essential concepts and physical origin of these ideas.
4.3. Hikosaka’s Sliding Diffusion Model
As aforementioned, the starting point of polymer crystallization is the folded chain model; however, under certain conditions, for instance, at elevated pressures, extended-chain crystals of some polymers can be obtained. Early studies can be traced back to Wunderlich and Arakawa [
109], who found that, at 5 K bar and 220 °C, PE could form extended-chain crystals. However, at that time, it was known that PE crystals are orthogonal and closely packed; therefore, large-scale thickening behavior, in principle, is inaccessible. This led Wunderlich [
110] to conjecture that, under high pressures, PE crystals will form a new phase with high mobility along the chain direction. This new phase, later known as the hexagonal phase, was originally observed by Bassett and Turner [
111,
112] and Yasuniwa [
113,
114]. It is a columnar phase, which has a two-dimensional long-range order and a one-dimensional short-range order. Along the thickness direction, the chain mobility is rather high; therefore, polymer chains can grow into extended-chain crystals.
Hikosaka [
115,
116,
117] subsequently proposed the sliding diffusion model to account for this phenomenon. The terminology of “chain sliding diffusion” can be defined as the self-diffusion of a polymer chain along its chain axis direction, probably surrounded by anisotropic potential field. The essence of this model is to introduce a two-dimensional growth mechanism and to take account of the topological nature of polymers. In addition to the traditional HL theory assuming the lateral growth, the diffusion motion can also occur along the chain direction, and the activated free energy of motion ∆
Es along the chain direction is proportional to the thickness of lamellar thickness
l, namely, ∆
Es~
Kl, where
K is a constant. In the orthogonal phase, chain slippage is quite difficult because ∆
Es is much greater than
kBT, while in the hexagonal phase, high mobility along the chain direction leads to a small value of
K.
Hikosaka’s sliding diffusion model provides a theoretical explanation of extended-chain crystals. In addition, the free energy barrier of sliding diffusion is proportional to the lamellar thickness, which effectively prevents the occurrence of δl-catastrophe.
Later detailed studies showed that, in PE crystals, at low pressures, the orthogonal phase is the stable phase; at high pressures, the hexagonal phase becomes the stable phase. Subsequently, Hikosaka et al. [
117] proposed that the crystallization process of PE usually had two distinct regimes. In one regime, lamellae can only grow with a specific thickness; in the other regime, the crystal firstly formed a hexagonal phase, then kept growing along both the lateral and chain directions until the hexagonal phase transformed into the orthogonal phase, or crystal impingement occurred. The transformation from the hexagonal phase to the orthogonal phase indicated that phase stability is related to phase dimension, which is quite interesting, but is beyond the scope of this article. Interested readers can resort to the original paper of Cheng and Keller [
118].
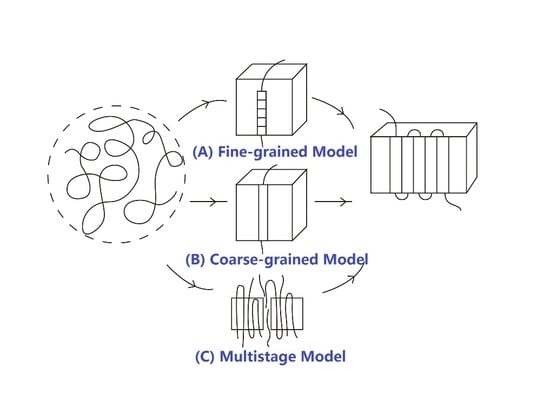
The concept of the hexagonal phase that is similar to the liquid crystalline phase with high mobility was subsequently generalized by Strobl [
119], who argued that it was a common intermediate state during polymer crystallization. This is the so-called “multi-stage model,” and we will discuss it in the following section.
In addition to PE crystals, there are a few systems that can also obtain extended-chain crystals. For instance, polyvinylidene difluoride [
120,
121], polytetrafluoroethylene [
122], polychlorotrifluoroethylene [
123], trans-1,4-polybutadiene [
124,
125,
126,
127], and polyethylene terephthalate [
128,
129,
130].
Finally, we make some personal comments on the Hikosaka’s model: it should be said that sliding diffusion mechanism is an important supplement to the traditional folding chain model, which provides a theoretical explanation for lamellar thickening. Moreover, the topological nature and chain entanglement effect are taken into account in an explicit manner. Recently, Hikosaka [
131] found that both primary nucleation and lateral growth rates showed power-law dependence on molecular weight, which confirmed that the topological nature of polymer chains assumes the most important role during polymer crystallization. Therefore, chain sliding diffusion motion may play a significant role both in primary and secondary nucleation processes.
4.4. Wunderlich’s Molecular Nucleation Theory
This concept was originally derived from the molecular segregation phenomenon. If two chemically identical components with different molecular weights (termed as “bimodal”) are mixed together, a question may arise: How to separate them? An immediate answer is as follows: Since the different molecular weights correspond to different equilibrium melting points, if we fixed the crystallization temperature between two equilibrium melting points, the component with high molecular weight would crystallize, while the low molecular one would not. Obviously, this separation method is based on the concept of thermodynamics and frequently referred to as
fractionation [
132].
However, it was observed that, even when the crystallization temperature was several centigrade degrees lower than the equilibrium melting point of the small molecular weight sample, crystallization stopped. Therefore, this separation approach is irrelevant to thermodynamics; instead, it is attributed to the kinetic effect, which is usually called
segregation. Compared with short-chain molecules, long-chain molecules appear to crystallize more easily. Therefore, from the experimental results, it looks as if each chain has to undergo its own process of nucleation. This conjecture is called the “molecular nucleation” mechanism [
133].
Another well-known example relevant to molecular segregation is the formation of spherulites [
134,
135,
136]. It has been observed that, for polydisperse polymers, the long-chain fractions are enriched in the early stage, leading to thicker lamellae termed as the “dominant lamellae”; in the later-grown crystals, short-chain fractions are enriched, resulting in thinner lamellar crystals called subsidiary lamellae. According to Keith-Padden’s phenomenological theory, the occurrence of branching is attributed to the fractionation of polymers, together with the segregation of impurities during the formation of spherulites [
137].
The phenomena of fractionation as well as segregation may be quite unique in polymer crystallization distinguished from those of small molecules [
58]. Obviously, these observations violate the HL theory since, in the HL model, there is no explicit molecular weight dependence except the kinetic prefactor
β [
83], which is, however, physically irrelevant to the present argument.
Furthermore, the “critical molecular length” can be defined for the PE samples with wide distribution of molecular weight [
135]. Beyond the critical molecular weight, components can crystallize, while samples cannot crystallize below the critical molecular weight, which is inconsistent with the theoretical calculation of the HL theory.
Molecular nucleation theory provides a theoretical explanation of the molecular segregation phenomenon, or, more generally, of molecular weight dependence during the polymer crystallization process. Meanwhile, it revises the opinion of the LH theory; a polymer chain rather than partial segments must form a stable nucleus, which was later supported by computer simulations [
138].
Another alternative interpretation may also be responsible for the phenomenon of molecular weight segregation. It can be estimated that the typical growth rates corresponding to polymer crystallization (10
−3–10 μm/h) [
139,
140] are orders of magnitude lower than that expected in the diffusion-controlled crystal growth (10–10
5 μm/h) [
141,
142]. This implies that a polymer chain has to “wait” a sufficiently long time in front of the crystal facet before it can be incorporated into the crystal. This is exactly the idea of nucleation theories! Therefore, many instances of surface attachment/detachment will be conducted, and the most stable configuration will eventually be chosen. This immediately leads to the competition between two components with different molecular weights on the surface [
143,
144,
145]. The low molecular weight fraction will be kinetically equilibrated first; however, the long-chain fraction will be thermodynamically more stable since it can obtain more contact energy. Hence, the higher molecular component continues to replace the lower one; as a result, segregation occurs. Therefore, it must be noted that the nucleation theory is only a possible explanation; any kinetic process depending on molecular weight may lead to a similar result.
4.5. Hu’s Intra-Molecular Nucleation Theory
Despite the early treatment of molecular segregation proposed by Wunderlich, the molecular weight dependence within polymer crystallization was still poorly understood. For example, there was no quantitative calculation to support the mechanism of chain segregation until Hu et al. [
41] proposed a simplified single-chain model to take this issue into account. They assumed that the molecular chain is arranged in a three-dimensional lattice. The degree of polymerization of the chain is N, and the number of uncrystalline units is n. The free energy difference can thus be explicitly calculated in the following way.
Assuming that the system is originally in crystalline phase and the energy required for each formation of an amorphous unit is
Ep, the energy cost will be (
q−2)
nEp/2, where q is the coordination number. However, once the amorphous unit forms, its orientation can be arbitrary, resulting in a certain amount of entropy compensation. The entropy gain corresponding to one monomer entropy should be ln(
q−1); for
n amorphous monomers, the resulting free energy gain will be
kTnln(
q−1). Therefore, the bulk free energy change can be estimated as
In addition, surfaces will be created between the crystalline and amorphous phases. For primary nucleation, due to the three-dimensional shape of the nucleus, the corresponding surface free energy scales as (N−n)2/3, whereas, for secondary nucleation, the relevant surface free energy is proportional to (N−n)1/2 since a two-dimensional nucleus is concerned.
Therefore, the total energy difference for primary nucleus can be estimated as
This simplified model gives an explicit expression of the free energy difference, which can be directly calculated by numerical methods. Hu et al. note that, at a fixed temperature, the nucleation barrier (∆Fc) is independent of the molecular weight, while the melting barrier (∆Fm) depends on the molecular weight.
It is obvious that the melting barrier will be higher when the molecular weight increases. Therefore, only when the molecular weight exceeds a critical molecular weight, the nucleus will not dissolve into the melt and the crystalline segments can survive. Therefore, the above arguments have explained the molecular weight dependence during polymer crystallization.
Now we can return to the issue of secondary nucleation (the previous arguments are related to primary nucleation). This simplified model allows us to make an explicit estimation of the “critical chain length” proposed by Wunderlich [
135]. It is obvious that the critical chain length corresponds to the situation when the crystallization barrier and the melting barrier are equal to each other:
where ∆
Fc2D and ∆
Fm2D correspond to the energy barrier of formation and the melting of the secondary nucleus, respectively. The critical molecular weight
Nc is inversely proportional to the square of the free energy difference, which is, equivalently, inversely proportional to the square of supercooling, in agreement with the experimental data of PE reported by Wunderlich.
In addition, Mehta and Wunderlich [
135] also proposed an upper bound of molecular weight during the molecular segregation process, namely, once the short-chain fraction exceeded the upper limit, the segregation phenomenon would no longer occur. This limit was subsequently confirmed by Glaser and Mandelkern [
146]. It is now easy to understand by using this simplified model. If the free energy of the melting barrier increases with the increase of
N, when
N exceeds a certain value, the melting barrier will be much larger than the crystallization barrier, indicating that the melting process will not occur.
In addition, Hu et al. noticed a significant defect in the molecular nucleation theory, namely, when the chain is long enough, the crystal growth front with a finite size is unlikely to feel the existence of the whole chain. One possible mechanism may lie in the fact that, as long as the sequential segments (rather than the whole chain) are sufficient, they can grow into the crystal, and the remaining amorphous part can further crystallize if its chain length is larger than the critical molecular length (see
Figure 2). There may be multiples reason for the formation of the partial amorphous chain, namely, by the impingement of other crystallites or by the constraint imposed through long-range topological entanglements. Crystallization in the same or different lamellae will lead to loops or tie molecules, respectively. Furthermore, when the crystallization temperature is lower, the corresponding critical chain length becomes shorter; therefore, at low temperatures, the polymer crystallization process will be rapid, and each polymer chain may pass through multiple lamellae or through the same lamella many times. This image is similar to the variable cluster model [
73], as well as to the widely spaced stem cluster model [
147,
148].
Compared to the HL theory, the intramolecular nucleation model does not need to introduce the hypothesis that the first deposited stem assumes the total nucleation barrier. Moreover, it also does not require the assumption of smooth crystal fronts in large scale, as long as the growth fronts can be relatively smooth locally.
On the basis of the intramolecular nucleation model, Hu et al. have successfully explained various well-known phenomena in polymer crystallization, such as chain folding, molecular segregation, and regime phenomenon, and computer simulation results support their conclusions [
149].
From a theoretical viewpoint, the intramolecular model combines reasonable aspects of various theories together and presents a more appropriate description. It provides a quantitative explanation of molecular segregation phenomenon and agrees with experiments quite well. In addition, the intramolecular model takes the topological structure of polymers into account and derives explicitly analytic expression of the minimum molecular weight dependence on supercooling based on a simplified model. Obviously, the intramolecular nucleation model takes a significant step in understanding the crystallization behavior of long-chain molecules.
4.6. Muthukumar’s Continuum Theory
Generally speaking, polymer crystallization can be classified into two categories: one is valid for melt-grown crystals and solution-grown crystals with relative high molecular weight, in which the crystal growth rate
G is nucleation-controlled and exponentially depends on 1/
T∆
T; the other is valid for solution-grown crystals with relative low molecular weight (
Mw), in which the growth rate
G is diffusion-controlled and linearly proportional to supercooling ∆
T [
150,
151].
Another remarkable feature of polymer crystallization is the significant dependence of the crystallization rate on Mw. It can be expected that, in a concentrated solution or even in a melt, the entanglement effect must be crucial for high polymers, which strongly depend on molecular weight as well as concentration; however, for solution-grown crystals with a low molecular weight, the transport effect may dominate. Therefore, to some extent, these two variables are unique to macromolecules, which distinctively separate polymer crystallization from small molecular crystallization. However, the mechanism of dependence on Mw and concentration is still partially understood and various explanations coexist.
Muthukumar et al. [
152] developed a unified formalism to take the two kinetic regimes into account. The key element of this continuum theory is to invoke an entropic barrier that originates from the accumulation of polymer chains near the crystal front. Experiments and simulations demonstrate the congestion of chain-like objects, even for rather dilute solutions, which leads to an entropic pressure, together with the influence of an excluded volume effect. Due to the higher concentration at the crystal front, the un-crystalline chains are subject to mutual penetration, and accessible configurations will hence be reduced. Therefore, these polymer chains must negotiate the entropic barrier before their incorporation into crystals. Based on this simple physical picture, two distinct regions can be identified. One is termed as the “inner layer” or the “boundary layer” near the crystal front, while the other is termed as the “outer layer.” Polymer chains are subject to free diffusion only in the outer layer, whereas in the boundary layer they are exerted to entropic force. Therefore, the dense inner layer enforces different dynamics from the outer layer, and, as a natural consequence, the effects of Mw and concentration are involved.
In addition, due to the arbitrary division of these two regions, the boundary condition must match the common interface. Under the steady-state condition, a continuum coarse-grained model of polymer crystallization focusing on detailed dynamics can be constructed. The specific free energy profile will significantly depend on how polymer chains organize within the boundary layer, corresponding to the detailed dynamics of polymers. Obviously, this description is in contrast to the case only considering energy contribution. Here, we must note, however, that the concept of “surface free energy” still holds in this barrier layer theory. The degeneracy due to possibility and energetic equivalence for stems to organize themselves on the crystal front gives rise to the surface free energy at the very first place. In this model, the stems are still subject to this kind of degeneracy at the growth front after they reconcile the entropic barrier layer adjacent to the front.
The conclusive analytical result can be summarized as the following expression:
where
G is the linear growth rate,
C0 is the initial concentration,
Din is the diffusion coefficient inside the boundary layer, ∆
H is the enthalpy of fusion, ∆
T is the under-cooling,
Tm is the melting temperature at the finite molecular weight,
Tc is the crystallization temperature, and
P is a parameter that depends on the details of the entropic barrier as well as on ∆
H,
Tm, and
Tc. The above expression captures the two kinetic regimes both for nucleation-controlled (
G ~ exp(−1/∆
T)) and diffusion-controlled (
G ~ ∆
T).
The concentration and molecular weight dependences have been assumed to obey different dynamics in the dense boundary zone compared with the outer layer. Based on this hypothesis, the growth rates can be evaluated to be weakly or marginally dependent on concentration (the exponent γ in G ~ Cγ is smaller or much smaller than 1). This is not surprising since the enrichment of polymer chains near the front considerably eliminates the sensitivity to the overall macromolecular concentration. These predictions agreed with the experimental results and implied a barrier control near the growth front. Therefore, based on the novel concept of entropic barrier within the boundary layer, a unified theory with reaction-diffusion type has been established. This model explicitly takes the characteristics of long-chain polymers into account and reveals the effects of concentration and molecular weight in a quantitative manner. The topological structure of chain-like objects is one of the most significant features of polymers, and the incorporation of the detailed dynamics of polymer motion inevitably deepens our understanding of polymer crystallization.
In summary, in this section, we mainly focus on the surface nucleation theories, namely, the secondary nucleation theories. The basic assumptions in various theories are highlighted since different theories will, to some extent, lead to the same experimental conclusions. Therefore, understanding the validity of their assumptions will be crucial. So far, most of the theories are kinetic in nature. The construction of them can be roughly divided into two competitive factors, one is the driving force and the other is the nucleation barrier. Different kinetic theories assume the same driving force, which originates from the Gibbs free energy change between the crystalline and amorphous phases. The divergence results from the definition of the nucleation barrier. Diverse factors are believed to be the rate-determining process in various theories. The various ingredients built in the kinetic model leads to complete distinct formalism. Here, we put some typical microscopic models in
Figure 6 together and hope that the similarities and differences between various models are self-evident. In fact, any theory that reasonably includes the driving force and the nucleation barrier will certainly result in similar conclusions. From this perspective, the kinetic theory is rather powerful since it can accommodate different elements. However, it should be noted that the nucleation barrier cannot be controlled by a single factor of enthalpy or entropy, comprehensive considerations will eventually lead to a more clear figure.
5. Primary Nucleation
In the previous section, we mainly discussed the surface nucleation theories, in which we assume that the system has well-defined preexisting crystal fronts, either flat or rough at the microscopic level. However, in recent decades, with the development of experimental techniques, especially the application of scattering approaches in polymer science, dramatic advances in the understanding of the early stages of crystallization (usually termed as “primary nucleation”) have been achieved, and a great amount of models have been proposed. In this section, we will introduce and present comparisons of various primary nucleation theories. However, it must be emphasized that the theories mentioned here address both primary and secondary nucleation processes. Nevertheless, in order to highlight these theories in the same context to compare their similarities and differences, we hope that such an arrangement will not lead to confusion.
As is known, crystallization is a first-order transition. Here, we first present some general physical pictures of phase transitions and show the main streams of current investigation. It is hoped that the establishment of an “overall picture” will help us to gain a deep insight into the phase transitions involved in polymer crystallization.
Generally speaking, there are two different mechanisms in phase separation. One is the nucleation and growth process (NG) and the other is the spinodal decomposition (SD). The two kinds of mechanisms deserve some comments here. Although both of them lead to phase separation, there are remarkable distinctions between them: (I) They occur at different regions. NG takes effect in a metastable region, while SD dominates in an unstable region. (II) Since they occur in different regions, the corresponding kinetic process are different. In the unstable region, the second derivative of free energy with respect to the order parameter is negative, so any tiny local concentration fluctuations will decrease the free energy. Hence, SD is a spontaneous process without any “barrier.” On the other hand, the second derivative of free energy with respect to the order parameter is positive in metastable regions. An energy barrier must be overcome by random thermal fluctuation leading to the stable “critical nuclei.” Thus, NG is responsible for this kind of phase separation. (III) The morphology will be different. SD corresponds to a zero “barrier” process, and spontaneous fluctuation can happen at any location of the system, which results in a bicontinuous texture. However, NG rests on local large concentration fluctuations to nucleation; therefore, it sporadically occurs in the system, leading to a sea-island structure. Of course, in the late stage, due to surface tension, bicontinuous structure breaks up and eventually coarsens into the sea-island structure. Nonetheless, in the early stage of phase separation, there are sharp differences between the morphologies of the two mechanisms.
In summary, for nucleation and growth (NG), relevant perturbation is small in extent but large in amplitude; therefore, the metastable state relaxes by the activated growth of localized density fluctuations of large amplitude. For SD, however, relevant perturbation is large in extent but small in amplitude; therefore, an unstable state relaxes by the spontaneous growth of long-wavelength fluctuations of small amplitude [
153].
Studies on the early stage of crystallization mainly rest on two distinct approaches. One is from a “solid” perspective, i.e., we can extrapolate the crystallization process from the final crystal structures, since it is believed that the final crystal morphology and structure actually reflect the true crystallization process. The other is from a “liquid” view, i.e., we need to examine the correlation function of the system, since, in the early stage, there are no crystallographic crystals. The system, to a large extent, is still in an undercooled amorphous state. For liquid states, the most direct approach is to explore the correlation function by means of a scattering technique.
From the “solid” perspective, a typical approach is to employ the “droplet” method. For instance, Vonnegat [
154] broke liquid film into tiny droplets of a few microns. The droplet was so small that most of them did not include heterogeneous nuclei; therefore, it was an ideal system to examine homogeneous nucleation, which could be directly observed under an optical microscope. Subsequent studies showed that the dimension of primary nucleus was about 10 nm
3, which is much smaller than the volume size of a whole macromolecule (about 100–1000 nm
3). It was concluded that the primary nucleus is only part of the macromolecular chain. Therefore, it is possible to prepare the so-called “single-chain, single crystals” to study the primary nucleation process [
155]. Bu et al. successfully prepared the single-chain crystals of PEO [
17]. In addition, similar results can also be obtained from other polymer systems, such as i-PS [
156] and PTFE [
157]. These evidences indicate that the primary nucleation follows the classical NG mechanism.
On the other hand, from the “liquid” perspective, a scattering technique has been applied to study the correlation function, and the situation is completely different. The scattering experiment will eventually give a time-averaged scattering curve. Meanwhile, the interpretation of the curve depends on the mathematical model employed. Early studies of the undercooled polymeric liquid found that, in addition to the expected correlation length around 2~3 nm, a large-scale correlation up to 300 nm can also be observed [
158]. In small molecules, a similar result could be found as well [
159]. Further studies [
160,
161,
162] showed that the two length scales were decoupled with respect to the long-range fluctuation correlation, which indicated that there should be some certain large-scale structure within the super-cooled liquid, since correlation is exactly equivalent to structure.
In addition to the large-scale correlation length, more sophisticated scattering experiments demonstrated that the system has the following kinetic features [
163,
164,
165,
166,
167]:
(1) Before any signals could be detected from wide angle X-ray diffraction, i.e., no crystallographic crystals formed, the plotted scattering curve of the integrated intensity I(q,t) versus q showed a peak qmax, which scaled as qmax~(∆T)1/2, where ∆T represents supercooling.
(2) I(q) exponentially grew with time, and the growth rate Ωq/q2 presented a linear relation with respect to q2 for intermediate values of q.
These observations are very similar to the kinetics of spinodal decomposition, and several researchers have proposed that the early crystallization process was dominated by the mechanism of SD rather than NG. However, from previous analyses, it can be seen that NG and SD are quite different—to some extent, they are incompatible.
Taking the SD mechanism to explain the formation of primary nuclei was firstly proposed by Imai et al. [
167], and later discussed by Olmsted et al. [
164]. According to the experimental scattering curves, they found that these curves were similar to the kinetics of the phase separation of the traditional polymer blends, which inspired them to propose that the formation of primary nuclei was a spinodal-assisted process. However, SD here is not relevant to the traditional phase separation of polymer blends; instead, it refers to the so-called “conformational separation.” They argued that, in the PE melt, since the temperature was high, the occurrence of various conformations was equally probable. According to the assumption of the rotational isomeric state, at high temperatures, the probability of trans- and gauche- (g+, g−) conformations was 1/3 and 2/3, respectively. When the temperature is below the melting point, the trans-conformation will aggregate and form the primary nuclei. In addition, they calculated the difference of the free energy barrier before and after phase separation and found that, due to phase separation, the nucleation barrier of crystallization would be considerably reduced. Therefore, they concluded that primary nuclei could form by a spinodal-assisted mechanism.
Subsequently, a similar mechanism termed as the “conformation-assisted fluctuation of density” was proposed by Yan et al. [
168]. They argued that, when the temperature was lower than the melting point, in addition to the density fluctuation, conformational fluctuation should also be taken into account. The starting point of this theory was to construct an appropriate free energy function of the Ginzburg–Landau-type and substitute it into the Cahn–Hilliard equation, and the evolution of the system could thus be obtained.
One of the essential parts of the aforementioned theories lies in that these authors realized that the undercooled liquid may be heterogeneous rather than homogeneous. However, attention must be paid to the following aspects: (1) If the formation of primary nuclei stemmed from conformational separation, the corresponding time scales would probably mismatch. The dynamic transition of trans- and gauch-conformations is in the range of 10
−11~10
−13 s, while the experimental detection of nuclei may occur at the time scale of seconds to minutes. The difference of several orders of magnitude and why the completion of conformational separation must wait several orders of magnitude before nucleation occurs are difficult to explain. (2) Some computer simulation results [
25,
84,
169,
170] and later scattering experiments [
171,
172] revealed that nucleation and growth mechanism still dominated primary nucleation, while other simulation results reported that spinodal decomposition preceded polymer crystallization [
173].
Muthukumar [
25,
84,
169,
170] employed Langevin dynamics to study the single-chain crystallization process, and they found that the snapshots demonstrated the following characteristics:
(i) Several regions of segmental aggregation with some visibly apparent local orientational orders are formed. Connected by the same chain, these regions are referred as “baby nuclei.”
(ii) As time evolves, the monomers in the flexible strands are reeled into the baby nuclei, and the orientational order in each nuclei increases.
(iii) Simultaneously, the competition between nuclei for further growth dissolves some nuclei.
It can be clearly seen that this process is exactly an NG process; the only difference is that, at this time, a polymer chain can participate in the formation of several nuclei since the polymer chain is very long.
In addition, it was also found that, during the simulation time, the spacing between baby nuclei remained unchanged, which was inversely proportional to the qmax. In the late stage of crystallization, the number of monomers involved in connectors gradually decreased, and the strands were reeled into baby nuclei, leading to the merge of some baby nuclei. This was followed by a cooperative reorganization, by which nuclei merged to form a single lamella. The mechanism of the merging was not via sequentially placing stems, but via a highly cooperative process, involving all stems of the lamella. Obviously, it is in contrast to the HL theory.
Later, Muthukumar [
25] considered the density fluctuation in an early stage. The starting point was still based on the Cahn–Hilliard equation and the considerable improvement was to introduce the new form of free energy. In the classical Cahn–Hilliard equation, the free energy obeys the Ginzburg–Landau functional form. Due to the non-local gradient term, the Fourier transform is frequently performed to decouple the non-local term into a local one. In Fourier space, one is the bulk term proportional to
ψ2, where
ψ is the order parameter in inverse space; the other corresponds to the interface term scaling as
q2ψ2, while Muthukumar added the third term
q−2ψ2, taking chain connectivity into account. It should be noted that the form of
q−2ψ2 is similar to the Debye structure factor within a distance less than the radius of gyration, which reflects the statistical properties of different monomers. Therefore, the constructed free energy reads
Substituting it into the Cahn–Hilliard equation, the following is obtained:
It should be noted that at this stage that both small and large q-values are cut off. Therefore, for a large q, it has the same predictions as the spinodal decomposition, namely, the plot of Ωq/q2 versus q2 presents a straight line with a negative slope. However, for small q regimes, the term q−2 dominates and Ωq/q2 versus q2 rapidly increases up to qmax, which is consistent with experiments.
To summarize, despite controversies over different mechanisms of primary nucleation, all theories have tried to clarify the origin of experimentally observed heterogeneous structures in the supercooled melt. Some kind of ordered structure, frequently referred to as a “preordered structure,” may exist. Various authors, in addition to the above-mentioned ones, including Hoffman [
69], who proposed this concept in his last review article, have stated a similar idea.
The “preordered structure” idea may be traced back to Allegra [
174,
175], who proposed that, prior to the formation of crystals, some kind of intra-molecular cluster (or bundles) with metastable equilibrium distributions first occurred in a liquid state. Furthermore, these clusters aggregated by van der Waals force and finally formed the crystal. This idea was generalized by Allegra and Meille [
176,
177], and the so-called “bundle theory” was proposed. The bundle is an aggregate of a few parallel polymer segments or stems connected by folds and stabilized by attractive crystal-like interactions.
From this point of view, the concept of a “bundle” is analogous to the idea of “baby nuclei” proposed by Muthukumar. However, Allegra and Meille argued that stems involved in one bundle originates from the same polymer chain in the context of a polymer solution, and these stems are connected by chain folds, while in bulk or concentrated solution, one bundle may include stems from distant chain portions, or even from different chains.
According to the original concept of the bundle theory, it may only apply to the case of a dilution solution. For melt crystallization, due to topological constraints, the mobility of polymer chains dramatic slowed down, resulting in the relaxation time of chain motion even longer than that of bundle stems. The mismatch of two time scales leads to a non-equilibrium process and cannot be treated in classical statistical thermodynamics.
Another key point of the bundle theory lies in that the lamellar crystal is formed by the transfer of stems from bundles to the lateral lamellar surface. Therefore, the lamellar thickness is largely determined by the statistical characteristics of stems in the bundle. However, it must be pointed out that the bundle theory is mainly a secondary nucleation theory, namely, it is assumed that crystal fronts are first formed by an aggregation of different bundles; hence, the subsequent growth process on the preexisting crystal fronts can be examined.
Dealing with the secondary nucleation theory is beyond the scope of this section. Interested readers can refer to the original papers [
176].
The starting point of the theoretical treatment of the bundle stem is to calculate the partition function. Here, only the case of polymer crystallization in a dilute solution will be introduced. When the polymer chain is in a liquid state, its partition function is assumed to be
Z0. When the temperature is below its melting temperature,
T0, the bundles will form and correspond to the following expression of the partition function:
where Ω
i is the multiplicity function, and
Ei is the attractive energy involved in the
i-th conformation. The subtracted term in the square brackets results from the fact that it has already been calculated in the reference state. Therefore, in order to avoid repeated computations, it must be subtracted. It should also be noted that the above formula employs the assumption that the temperature is in the vicinity of the equilibrium temperature
T0, namely, under small supercoolings. Once we have the partition function, the free energy can be readily obtained:
Compared with the thermodynamics derivations in
Section 2, it is not difficult to find that they both have the same expression, i.e., the free energy difference is proportional to supercooling. However, it should be noted that ∆
G corresponds to the bundle state rather than the crystalline state, which indicates that the same dependence is valid for both the intermediate metastable state and the equilibrium state. Therefore, we can infer that the statistical properties of bundles will determine the subsequent growth kinetics, which inevitably leads to similar results as mentioned previously.
In addition, in order to explain the difference between the re-crystallization line and the melting line observed in experiments, Strobl [
119,
178,
179,
180] also proposed the concept of the “mesomorphic phase.” He argued that there was a mesomorphic inner structure between the crystalline and amorphous phase, which was stabilized by epitaxial force. In addition, all stereo defects and noncrystalline co-units will be rejected on its fronts by the lateral growth. In this model, the mesomorphic phase requires a minimal dimension to maintain its stability in the melt condition. High inner mobility allows for the spontaneous thickening of a long-chain direction, which is similar to the sliding diffusion motion proposed by Hikosaka. However, the inner mobility will be reduced by lamellar thickening, which effectively prevents the occurrence of extended-chain crystals and leads to a limited lamellar thickness. In addition, the outside layer has a higher mobility than the inside layers, which leads to the “solidification” of inner parts and transforms to more perfectly ordered structures, frequently called “granular blocks.” These blocks then collide and combine with each other to form larger aggregates. Such transformation does not need much energy to overcome the free energy barrier. These aggregates further undergo “perfection” and eventually form the crystals with specific lamellar thickness. This process is usually termed as the “multi-stage model.”
From the above description, we can see that the multi-stage model proposed by Strobl is quite different from the traditional nucleation theory. Strobl introduces the third phase, i.e., the mesomorphic phase, and the traditional thermodynamic theories of crystallization merely take two phases into account, that is, they only consider the crystalline phase and the amorphous phase. This is the origin of introduction of the third phase by Strobl, who argued that the traditional treatment was insufficient. From experiments, it can be clearly seen that melting and crystallization follow two distinct pathways, which may be, in principle, irreversible. Obviously, it violates the classical nucleation theory and cannot be explained by the two-phase model.
Moreover, the introduction of the mesomorphic phase may also be inspired by the hexagonal phase proposed by Hikosaka. The most prominent merit of Strobl’s multistage model is that the thermodynamic parameters, such as the surface and bulk free energies of the intermediate state (mesophase) is different from those of the final crystals. The future theory for polymer crystallization should take the size effect into account. However, some authors have argued that the introduction of the mesomorphic phase would affect the correct formation of crystals by the random incorporation of blocks [
181,
182].
The concept of the “mesomorphic phase” is similar to that of the “bundle” proposed by Allegra. In Strobl’s model, the preordered structures with high inner mobility will undergo a self-perfection process and form granular blocks, and these blocks will then merge with each other and eventually form crystals. In accordance with the bundle theory, Allegra employed the traditional process, i.e., stems involved in the bundle diffuse and adsorb onto the crystal fronts. Furthermore, in Muthukumar’s simulation results, crystal growth is controlled by diffusion rather than surface nucleation, i.e., once a few segments contact the crystal fronts, the remaining parts of the chain quickly add to the crystal surfaces, which indicates that the addition of segments onto the crystal fronts corresponds to small energy barriers. On the contrary, in order to commensurate with the growth crystals, subsequent molecular rearrangement on the crystal surface is the rate-determining process. Moreover, the arrangement is a highly cooperative process involving participation of many molecular chains, and subsequent experiments and simulations clarify the “precursor” state more clearly [
183,
184,
185,
186,
187]. All these aspects are in contrast to traditional nucleation theories [
61].
Finally, we present three different typical routes relevant to the polymer crystallization process and the corresponding free energy landscapes in
Figure 7.
6. Conclusions
It is the aim of this article to review the major theories relevant to polymer crystallization. Basic assumptions of various theories are highlighted, and detailed discussions are performed in a physically intuitive way. We hope that such treatments will help readers to appreciate the beauty of each theory and recognize their successful and unsuccessful parts. Polymer crystallization features in the development of polymer science and the corresponding theories have been put forward for more than fifty years; however, new models or theories are still being proposed nowadays, which indicates that the field itself is essentially complex and robustly vital. Nevertheless, open questions remain in this field, and controversial opinions sometimes coexist. Here we give a short summary and present some personal views on the potential problems in polymer crystallization theories.
We firstly discuss the concept of chain folding in
Section 2, since it is one of the most significant features different from the crystallization of small molecules, as well as its physical implications, such as why a polymer chain needs to fold during crystallization. In
Section 3, we present the basic thermodynamic considerations, in which we especially focus on various defects and omissions behind the conventional treatment, which mainly stems from the finite size effect.
Section 4 and
Section 5 are the main parts of this paper, dealing with secondary and primary nucleation theories, respectively. In
Section 4, we firstly introduce the Hoffman–Lauritzen (HL) theory as the main line within this section because it provides a simple and analytical formalism to deal with polymer crystallization, as well as a reference model that was subsequently modified by other theories and models. In
Section 5, we mainly focus on primary nucleation theories, which share some similarities and, to some extent, overlap with each other, and we compare the different theories in an explicit way.
In the following, we will present some personal views on potential issues remaining in polymer crystallization theories.
(1) A topological long-chain nature is one of the most significant features of polymers, and should certainly be taken into account in any theory. So far, various authors have addressed this issue from apparently distinct perspectives. The most common approach is to invoke an entropic barrier, which may originate either from wrong configurations or from entropic pressure. In addition, the topological structure can also be implicitly treated by addressing the effects of entanglement, diffusion, and so on. Therefore, a natural question may be raised: Some treatments are rather microscopic while others, to some extent, are phenomenological. Are these descriptions equivalent or not? We can also further ask whether these descriptions are complete or not. Apparently, no theory can interpret all experimental results, and a fortiori make predictions about unknown phenomena of polymer crystallization. Therefore, we have to resort to the paradigm of how to appropriately describe the polymer crystallization process by compromising microscopic details and its physical nature; however, we do not know the answer at present.
(2) Polymer crystal is, in essence, a strong correlated system far from equilibrium. At equilibrium, statistical analysis can be employed to associate macroscopic quantities with microscopic parameters. Based on the self-similar property of polymers, scaling analysis could be successfully performed and lead to remarkable physical consequences. Nevertheless, for non-equilibrium systems along with strong correlations, it is uncertain whether scaling arguments could be valid. Recent studies on non-equilibrium systems [
188] found that, even under far from equilibrium conditions, unexpected long-range correlations may appear. Power-law behaviors indicate the potential application of scaling analysis; such a treatment, however, has seldom appeared in the literature.
(3) Recent studies on the early stage of crystallization reveal new phenomena that undercooled liquid may have a heterogeneous structure [
187]. Traditional crystallization theories are well established based on homogeneous primary nucleation; if the system is heterogeneous rather than homogeneous, many aspects relevant to polymer crystallization process should be reconsidered, and the pre-crystalline ordered state also presents a challenging issue against the conventional treatments.
(4) All the theories and models established for polymer crystallization can be divided into the subcategories according to the number of microscopic states and the treatment of the long-range multi-body interactions. Here, various microscopic states possess different sets of thermodynamic or kinetic parameters. For instance, HL theory is a two-state theory, where the interface free energy per area and bulk free energy per volume of polymer lamellae are independent of crystal size. In contrast, Strobl’s new model is a three-state model, in which the meso-phase and the stabilized crystal have different thermodynamic parameters. The treatment of long-range multi-body interaction in polymer lamellar crystals is tricky, which lies in the core of any crystallization theory. For the classical thermodynamic description, the long-range multi-body interaction enters the interfacial free energy term. In fact, the interfacial free energy may vary with crystal size when the crystal is very small, e.g., of nanometer scale. On the contrary, in some kinetics models, only the interaction between the nearest neighbors are considered, which is analogous to the treatment of phase separation and may have a limited value of energy barrier around several kBT if the interfacial free energy is not taken into account. As a result, this would lead to spinodal-like behavior. Consequently, the future new theory on polymer crystallization (or more generally on crystallization) should bear the ability to describe various intermediate states with long-range multi-body interaction. Microscopic kinetics model independent of the thermodynamics frame may be a potential candidate of the new crystallization theory.
(5) What is the relationship between polymer crystallization and other subjects such as glass transition? Both of them are strongly correlated with many body systems. Is there a unified framework to understand them? Glass transition also relates to physical aging, which is an important issue both in scientific research and industrial application. Besides, the phenomena relevant to lamellar thickening, melting, and/or recrystallization are frequently encountered. All of them are the physical consequences of the evolution from non-equilibrium to equilibrium. Unfortunately, we do not know exactly the rules controlling evolution except the Ostwald ripening principle. In addition, the final mechanical properties are largely determined by the structure, namely, the morphology of the crystals, which is further tightly connected with nucleation. Up to now, polymer crystallization theories mainly correspond to the nucleation process, and, of course, we need to develop more detailed theories relevant to superstructures, such as spherulites and oriented crystal structures formed in external force fields.