Indentation Plasticity and Fracture Studies of Organic Crystals
Abstract
:1. Introduction
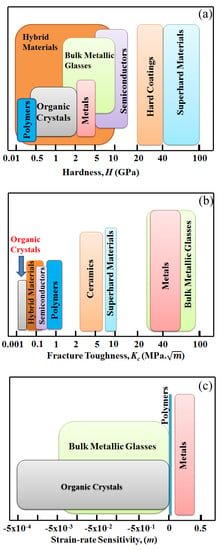
1.1. Mechanical Properties
1.2. Plasticity
1.3. The Critical Resolved Shear Stress and Schmid Factor
2. Hardness Measurement Methods
2.1. Prediction of Hardness Using Crystal Morphology
2.2. Factors Affecting Nanoindentation Hardness of Organic Crystals
3. Understanding the Plastic Behavior of Organic Crystals
3.1. Indentation Hardness of Molecular Crystals
3.1.1. Cyclotrimethylenetrinitramine, (RDX) Crystals
3.1.2. Hardness Anisotropy Studies in Some Organic Crystals
3.1.3. Mechanical Behavior of Aspirin Polymorphs
3.1.4. Mechanoluminiscence Studies in Difluoroavobenzone
3.1.5. Tuning of Hardness in Organic Crystals
Strengthening Organic Crystals by the Co-Crystallization Approach
3.1.6. Establishing a Correlation Between Hardness and Solubility
3.1.7. Indentation-Induced Plasticity in Parabens and Paracetamol
3.1.8. Establishing the Relation between Plastic Behavior in Bulk and Single Crystals of APIs
3.1.9. In Situ Nanoindentation to Study Disorders in APIs
3.1.10. Strain-Rate Sensitivity Studies
3.1.11. Nanoscratch Experiments: Anisotropy in Molecular Movements
3.1.12. AFM Nanoindentation to Study the Slip Planes
3.1.13. Real-Time Imaging of Indentation-Induced Structural Changes in Piroxicam
3.1.14. Phase Transformations under Applied Load
4. Fracture Behavior of Organic Crystals
5. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Varughese, S.; Kiran, M.S.R.N.; Ramamurty, U.; Desiraju, G.R. Nanoindentation in crystal engineering: Quantifying mechanical properties of molecular crystals. Angew. Chem. Int. Ed. 2013, 52, 2701–2712. [Google Scholar] [CrossRef] [PubMed]
- Egart, M.; Jankovi, B.; Lah, N.; Ilic, I.; Srcic, S. Nanomechanical properties of selected single pharmaceutical crystals as a predictor of their bulk behavior. Pharm. Res. 2015, 32, 469–481. [Google Scholar] [CrossRef] [PubMed]
- Loo, Y.L.; Someya, T.; Baldwin, K.W.; Bao, Z.; Ho, P.; Dodabalapur, A.; Katz, H.E.; Rogers, J.A. Soft, conformable electrical contacts for organic semiconductors: High-resolution plastic circuits by lamination. Proc. Natl. Acad. Sci. USA 2002, 99, 10252–10256. [Google Scholar] [CrossRef] [PubMed]
- Kim, W.; Palilis, L.C.; Uchida, M.; Kafafi, Z.H. Efficient silole-based organic light-emitting diodes using high conductivity polymer anodes. Chem. Mater. 2004, 16, 4681–4686. [Google Scholar] [CrossRef]
- Remenar, J.F.; Morissette, S.L.; Peterson, M.L.; Moulton, B.; Macphee, J.M.; Guzman, H.R.; Almarsson, O. Crystal engineering of novel cocrystals of a triazole drug with 1,4-dicarboxylic acids. J. Am. Chem. Soc. 2003, 125, 8456–8457. [Google Scholar] [CrossRef] [PubMed]
- Velaga, S.P.; Basavoju, S.; Bostrom, D. Norfloxacin saccharinate-saccharin dihydrate cocrystal—A new pharmaceutical cocrystal with an organic counter ion. J. Mol. Struct. 2008, 889, 150–153. [Google Scholar] [CrossRef]
- Kaiser, C.R.; Karlapais, C.; de Souza, M.V.N.; Wardell, J.L.; Solange, D.; Wardell, M.S.V.; Edward; Tiekink, R. Assessing the persistence of the n–h⋯n hydrogen bonding leading to supramolecular chains in molecules related to the anti-malarial drug, chloroquine. CrystEngComm 2009, 11, 1133–1140. [Google Scholar] [CrossRef]
- Schultheiss, N.; Newman, A. Pharmaceutical cocrystals and their physicochemical properties. Cryst. Growth. Des. 2009, 9, 2950–2967. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.C. Materials science tetrahedron—A useful tool for pharmaceutical research and development. J. Pharm. Sci. 2009, 98, 1671–1687. [Google Scholar] [CrossRef] [PubMed]
- Byrn, S.R.; Pfeiffer, R.R.; Stowell, J.G. Solid-State Chemistry of Drugs; Ssci, Inc.: West Lafayette, IN, USA, 1999. [Google Scholar]
- Reddy, C.M.; Krishna, G.R.; Ghosh, S. Mechanical properties of molecular crystals—Applications to crystal engineering. CrystEngComm 2010, 12, 2296–2314. [Google Scholar] [CrossRef]
- Mørch, Y.A.; Holtan, S.; Donati, L.; Strand, B.L.; Bræk, G.S. Mechanical properties of c-5 epimerized alginates. Biomacromolecules 2008, 9, 2360–2368. [Google Scholar] [CrossRef] [PubMed]
- Rosa, C.D.; Auriemma, F. Structural-mechanical phase diagram of isotactic polypropylene. J. Am. Chem. Soc. 2006, 128, 11024–11025. [Google Scholar] [PubMed]
- Patel, S.; Sun, C.C. Macroindentation hardness measurement-modernization and applications. Int. J. Pharm. 2016, 506, 262–267. [Google Scholar] [CrossRef] [PubMed]
- Courtney, T.H. Mechanical Behaviour of Materials, 2nd ed.; Waveland Press Inc.: Long Grove, IL, USA, 2008. [Google Scholar]
- Rupert, T.J.; Gianola, D.S.; Gan, Y.; Hemker, K.J. Experimental observations of stress-driven grain boundary migration. Science 2009, 326, 1686–1690. [Google Scholar] [CrossRef] [PubMed]
- Tresca, H. Memoire Sur 1’ecoulement des Corps Solides Soumis a Des Fortes Pressions. C. R. Acad. Sci. Paris 1864, 59, 754–758. [Google Scholar]
- Saint-Venant, B.D. Memoire sur I’etablissement des Equations Differentielles des Mouvements Interieurs Operes Dans Les Corps Solides Ductiles au Dela des Limites ou I’elasticite Pourrait Les Ramener a Leur Premier etat. C. R. Acad. Sci. Paris 1870, 70, 473–480. [Google Scholar]
- Levy, M. Memoire Sur Les Equations Generales des Mouvements Interieurs des Corps Solides Ductiles au Dela Limits ou 1’Elasticite Pourrait Les Rammener a LeurPpremier etat. C. R. Acad. Sci. Paris 1870, 70, 1323–1325. [Google Scholar]
- Vonmises, R. Mechanics of solids and shells: Theories and approximations. Göttin. Nachr. Math. Phys. 1913, 1, 582–592. [Google Scholar]
- Lin, J. Fundamentals of Materials Modelling for Metals Processing Technologies: Theories and Applications; Imperial College Press: London, UK, 2015. [Google Scholar]
- Prager, W. Introduction to the Mechanics of Continua; Dover Publications Inc.: Mineola, NY, USA, 1961. [Google Scholar]
- Hill, R. The Mathematical Theory of Plasticity; Clarendon Press: Oxford, UK, 1950. [Google Scholar]
- Eduardo, A.; Neto, D.S.; Djordjeperic; David, R.; Owen, J. Computational Methods for Plasticity: Theory and Applications; Wiley Publishers: Hoboken, NY, USA, 2008. [Google Scholar]
- Sherwood, J.N. The Plastically Crystalline State (Orientationally-Disordered Crystals); Sherwood, J.N., Ed.; Wiley: Chichester, UK, 1979. [Google Scholar]
- Roberts, R.J.; Rowe, R.C.; York, P. The relationship between indentation hardness of organic solids and their molecular structure. J. Mater. Sci. 1994, 29, 2289–2296. [Google Scholar] [CrossRef]
- Ramamurty, U.; Jang, J. Nanoindentation for probing the mechanical behavior of molecular crystals—A review of the technique and how to use it. CrystEngComm 2014, 16, 12–23. [Google Scholar] [CrossRef]
- Brinell, J.A. Way of determining the hardness of bodies and some applications of the same. Tek. Tidskr. 1900, 5, 69–87. [Google Scholar]
- Meyer, E. Investigations of hardness testing and hardness. Phys. Z. 1908, 9, 66–74. [Google Scholar]
- Hutchings, I.M. The contributions of David Tabor to the science of indentation hardness. J. Mater. Res. 2009, 24, 581–589. [Google Scholar] [CrossRef]
- Tabor, D. A simple theory of static and dynamic hardness. Proc. R. Soc. Lond. A 1948, 192, 247–274. [Google Scholar] [CrossRef]
- Tabor, D. The Hardness of Metals; Oxford University Press: Oxford, UK, 1951. [Google Scholar]
- King, R.F.; Tabor, D. The effect of temperature on the mechanical properties and the friction of plastics. Proc. Phys. Soc. B 1953, 66, 728–736. [Google Scholar] [CrossRef]
- Pascoe, M.W.; Tabor, D. The friction and deformation of polymers. Proc. R. Soc. A 1956, 235, 210–224. [Google Scholar] [CrossRef]
- King, R.F.; Tabor, D. The strength properties and frictional behaviour of brittle solids. Proc. Phys. Soc. A 1954, 223, 225–238. [Google Scholar] [CrossRef]
- Atkins, A.G.; Tabor, D. Mutual indentation hardness of single-crystal magnesium oxide at high temperatures. J. Am. Ceram. Soc. 1967, 50, 195–198. [Google Scholar] [CrossRef]
- Liu, M. Crystal Plasticity and Experimental Studies of Nano-Indentation of Aluminium and Copper. Ph.D. Thesis, University of Wollongong, Wollongong, Australia, 2014. [Google Scholar]
- Fischer-Cripps, A.C. A review of analysis methods for sub-micron indentation testing. Vacuum 2000, 58, 569–585. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic-modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Oliver, P. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 1–20. [Google Scholar] [CrossRef]
- Kucharski, S.; Mroz, Z. Identification of yield stress and plastic hardening parameters from a spherical indentation test. Int. J. Mech. Sci. 2007, 49, 1238–1250. [Google Scholar] [CrossRef]
- Kruzic, J.J.; Kim, D.K.; Koester, K.J.; Ritchie, R.O. Indentation techniques for evaluating the fracture toughness of biomaterials and hard tissues. J. Mech. Behav. Biomed. Mater. 2009, 2, 384–395. [Google Scholar] [CrossRef] [PubMed]
- Huber, N.; Tsakmakis, C. Experimental and theoretical investigation of the effect of kinematic hardening on spherical indentation. Mech. Mater. 1998, 27, 241–248. [Google Scholar] [CrossRef]
- Masri, R.; Durban, D. Cylindrical cavity expansion in compressible mises and tresca solids. Eur. J. Mech. A Solid. 2007, 26, 712–727. [Google Scholar] [CrossRef]
- Marsh, D.M. Plastic flow in glass. Proc. R. Soc. A 1964, 279, 420–435. [Google Scholar] [CrossRef]
- Rodriguez, J.; Rico, A.; Otero, E.; Rainforth, W.M. Indentation properties of plasma sprayed Al2O3-13% TiO2 nanocoatings. Acta Mater. 2009, 57, 3148–3156. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Page, T.F.; Oliver, W.C.; Mchargue, C.J. The deformation behavior of ceramic crystals subjected to very low load (nano) indentations. J. Mater. Res. 1992, 7, 450–473. [Google Scholar] [CrossRef]
- Bennet, D.W. Multi-Scale Indentation Hardness Testing: A Correlation and Model. Doctor’s Disertation, Oklahoma State University, Stillwater, OK, USA, 2008. [Google Scholar]
- Shibutani, Y.; Koyama, A. Surface roughness effect on the displacement bursts observed in nanoindentation. J. Mater. Res. 2004, 19, 183–188. [Google Scholar] [CrossRef]
- Agilent Technologies. Indentation Rules of Thumb-Applications and Limits; Agilent Technologies: Santa Clara, CA, USA, 2015. [Google Scholar]
- Qian, L.; Li, M.; Zhou, Z.; Yang, H.; Shi, X. Comparison of nanoindentation hardness to microhardness. Surf. Coat. Technol. 2005, 195, 264–271. [Google Scholar] [CrossRef]
- Kese, K.; Li, Z.C. Semi-Ellipse method for accounting for the pile-up contact area during nanoindentation with the berkovich indenter. Scr. Mater. 2006, 55, 699–702. [Google Scholar] [CrossRef]
- Choi, Y.; Lee, H.S.; Kwon, D. Analysis of sharp-tip-indentation load-depth curve for contact area determination taking into account pile-up and sink-in effects. J. Mater. Res. 2004, 19, 3307–3315. [Google Scholar] [CrossRef]
- Karthik, V.; Visweswaran, P.; Bhushan, A.; Pawaskar, D.N.; Kasiviswanathan, K.V.; Jayakumar, T.; Raj, B. Finite element analysis of spherical indentation to study pile-up/sink-in phenomena in steels and experimental validation. Int. J. Mech. Sci. 2012, 54, 74–83. [Google Scholar] [CrossRef]
- Zhou, X.; Jiang, Z.; Wang, H.; Yu, R. Investigation on methods for dealing with pile-up errors in evaluating the mechanical properties of thin metal films at sub-micron scale on hard substrates by nanoindentation technique. Mater. Sci. Eng. A. 2008, 488, 318–332. [Google Scholar] [CrossRef]
- Nix, W.D.; Gao, H. Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Sol. 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Budiman, A.S. Indentation Size Effects in Single Crystal Cu as Revealed by Synchrotron X-ray Microdiffraction. In Probing Crystal Plasticity at the Nanoscales; Springer: Singapore, 2014; pp. 87–101. [Google Scholar]
- Reddy, C.M.; Gundakaram, R.C.; Basavoju, S.; Kirchner, M.T.; Padmanabhan, K.A.; Desiraju, G.R. Structural basis for bending of organic crystals. Chem. Commun. 2005, 31, 3945–3947. [Google Scholar] [CrossRef] [PubMed]
- Reddy, C.M.; Padmanabhan, K.A.; Desiraju, G.R. Structure-property correlations in bending and brittle organic crystals. Cryst. Growth Des. 2006, 6, 2720–2731. [Google Scholar] [CrossRef]
- Reddy, C.M.; Kirchner, M.T.; Gundakaram, R.C.; Desiraju, G.R. Isostructurality, Polymorphism and mechanical properties of some hexahalogenated benzenes: The nature of halogen—Halogen interactions. Chem. Eur. J. 2006, 12, 2222–2234. [Google Scholar] [CrossRef] [PubMed]
- Panda, M.K.; Ghosh, S.; Yasuda, N.; Moriwaki, T.; Mukharjee, G.D.; Reddy, C.M.; Naumov, P. Spatially resolved analysis of short-range structure perturbations in a plastically bent molecular crystal. Nat. Chem. 2015, 7, 65–72. [Google Scholar] [CrossRef] [PubMed]
- Thomas, S.P.; Shi, M.W.; Koutsantonis, G.A.; Jayatilaka, D.; Edwards, A.J.; Spackman, M.A. The elusive structural origin of plastic bending in dimethyl sulfone crystals with quasi-isotropic crystal packing. Angew. Chem. Int. Ed. 2017, 56, 8468–8472. [Google Scholar] [CrossRef] [PubMed]
- Saha, S.; Desiraju, G.R. Crystal engineering of hand-twisted helical crystals. J. Am. Chem. Soc. 2017, 139, 1975–1983. [Google Scholar] [CrossRef] [PubMed]
- Hagan, J.T.; Chaudhri, M.M. Fracture surface energies of high explosives PETN and RDX. J. Mater. Sci. 1977, 12, 1055–1058. [Google Scholar] [CrossRef]
- Halfpenny, P.J.; Roberts, K.J.; Sherwood, J.N. Dislocations in energetic materials. J. Mater. Sci. 1984, 19, 1629–1637. [Google Scholar] [CrossRef]
- Chaudhri, M.M. The junction growth equation and its application to explosive crystals. J. Mater. Sci. Lett. 1984, 3, 565–568. [Google Scholar] [CrossRef]
- Elban, W.L.; Hoffsommer, J.C.; Armstrong, R.W. X-ray orientation and hardness experiments on RDX crystals. J. Mater. Sci. 1984, 19, 552–566. [Google Scholar] [CrossRef]
- Elban, W.L.; Armstrong, R.W.; Yoo, K.C. X-ray reflection topographic study of growth defect and microindentation strain fields in an RDX explosive crystal. J. Mater. Sci. 1989, 24, 1273–1280. [Google Scholar] [CrossRef]
- Gallagher, H.G.; Miller, J.C.; Sheen, D.B.; Sherwood, J.N.; Vrcelj, R.M. Mechanical Properties of β-HMX. Chem. Cent. J. 2015, 9, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, C.C.; Kiang, Y.H. On the identification of slip planes in organic crystals based on attachment energy calculation. J. Pharm. Sci. 2008, 98, 3456–3461. [Google Scholar] [CrossRef] [PubMed]
- Ramos, K.J.; Hooks, D.E.; Bahr, D.F. Direct observation of plasticity and quantitative hardness measurements in single crystal cyclotrimethylene trinitramine by nanoindentation. Philos. Mag. 2009, 89, 2381–2402. [Google Scholar] [CrossRef]
- Ramos, K.J.; Bahr, D.F.; Hooks, D.E. Defect and surface asperity dependent yield during contact loading of an organic molecular single crystal. Philos. Mag. 2011, 91, 1276–1285. [Google Scholar] [CrossRef]
- Weingarten, N.S.; Sausa, R.C. Nanomechanics of RDX single crystals by force-displacement measurements and molecular dynamics simulations. J. Phys. Chem. A 2015, 119, 9338–9351. [Google Scholar] [CrossRef] [PubMed]
- Connick, W.; May, F.G.J. Dislocation etching of cyclotrimethylene trinitramine crystals. J. Cryst. Growth 1969, 5, 65–69. [Google Scholar] [CrossRef]
- Munday, L.B.; Solares, S.D.; Chung, P.W. Generalized stacking fault energy surfaces in the molecular crystal A-RDX. Philos. Mag. 2012, 92, 3036–3050. [Google Scholar] [CrossRef]
- Mathew, N.; Picu, R.C. Slip asymmetry in the molecular crystal cyclotrimethylenetrinitramine. Chem. Phys. Lett. 2013, 582, 78–81. [Google Scholar] [CrossRef]
- Taw, M.R.; Bahr, D.F. The mechanical properties of minimally processed RDX. propellants Explos. PyrTech. 2017, 42, 659–664. [Google Scholar] [CrossRef]
- Liu, J.; Zeng, Q.; Zhang, Y.; Zhang, C. Limited-Sample coarse-grained strategy and its applications to molecular crystals: Elastic property prediction and nanoindentation simulations of 1,3,5-trinitro-1,3,5-triazinane. J. Phys. Chem. C 2016, 120, 15198–15208. [Google Scholar] [CrossRef]
- Joshi, M.J.; Shah, B.S. On the microhardness of some molecular crystals. Cryst. Res. Technol. 1984, 19, 1107–1111. [Google Scholar] [CrossRef]
- Marwaha, R.K.; Sha, B.S. A study on the microhardness of organic molecular solids. Cryst. Res. Technol. 1991, 26, 491–494. [Google Scholar] [CrossRef]
- Sgualdino, G.; Vaccari, G.; Mantovani, G. Sucrose crystal hardness: A correlation with some parameters defining the growth kinetics. Cryst. Growth 1990, 140, 527–532. [Google Scholar] [CrossRef]
- Elban, W.; Sheen, D.; Sherwood, J.N. Vickers hardness testing of sucrose single-crystals. J. Cryst. Growth 1994, 137, 304–308. [Google Scholar] [CrossRef]
- Ramos, K.J.; Bahr, D.F. Mechanical behavior assessment of sucrose using Nanoindentation. J. Mater. Res. 2007, 22, 2037–2045. [Google Scholar] [CrossRef]
- Kiran, M.S.R.N.; Varughese, S.; Reddy, C.M.; Ramamurty, U.; Desiraju, G.R. Mechanical anisotropy in crystalline saccharin: Nanoindentation studies. Cryst. Growth Des. 2010, 10, 4650–4655. [Google Scholar] [CrossRef]
- Zhou, X.; Lu, Z.; Zhang, Q.; Chen, D.; Li, H.; Fudenie; Zhang, C. Mechanical anisotropy of the energetic crystal of 1,1-diamino-2,2-dinitroethylene (fox-7): A study by nanoindentation experiments and density functional theory calculations. J. Phys. Chem. C 2016, 120, 13434–13442. [Google Scholar] [CrossRef]
- Mathew, N.; Sewell, T.D. Nanoindentation of the triclinic molecular crystal 1,3,5-triamino-2,4,6-trinitrobenzene: A molecular dynamics study. J. Phys. Chem. C 2016, 120, 8266–8277. [Google Scholar] [CrossRef]
- Taw, M.R.; Yeager, J.D.; Hooks, D.E.; Carvajal, T.M.; Bahr, D.F. The mechanical properties of as-grown non-cubic organic molecular crystals assessed by nanoindentation. J. Mater. Res. 2017, 32, 2728–2737. [Google Scholar] [CrossRef]
- Varughese, S.; Kiran, M.S.R.N.; Solanko, K.A.; Bond, A.D.; Ramamurty, U.; Desiraju, G.R. Interaction anisotropy and shear instability of aspirin polymorphs established by nanoindentation. Chem. Sci. 2011, 2, 2236–2242. [Google Scholar] [CrossRef]
- Olusanmi, D.; Roberts, K.J.; Ghadiri, M.; Ding, Y. The breakage behaviour of aspirin under quasi-static indentation and single particle impact loading: Effect of crystallographic anisotropy. Int. J. Pharm. 2011, 411, 49–63. [Google Scholar] [CrossRef] [PubMed]
- Krishna, G.R.; Kiran, M.S.R.N.; Fraser, C.L.; Ramamurty, U.; Reddy, C.M. The relationship of solid state plasticity to mechanochromic luminescence in Difluoroboron avobenzone polymorphs. Adv. Funct. Mater. 2013, 23, 1422–1430. [Google Scholar] [CrossRef]
- Mishra, M.K.; Ramamurty, U.; Desiraju, G.R. Solid solution hardening of molecular crystals: Tautomeric polymorphs of omeprazole. J. Am. Chem. Soc. 2015, 137, 1794–1797. [Google Scholar] [CrossRef] [PubMed]
- Sanphui, P.; Mishra, M.K.; Ramamurty, U.; Desiraju, G.R. Tuning mechanical properties of pharmaceutical crystals with multicomponent crystals: Voriconazole as a case study. Mol. Pharm. 2015, 12, 889–897. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.J.; Kavuru, P.; Wojtas, L.; Zaworotko, M.J.; Shytle, R.D. Cocrystals of quercetin with improved solubility and oral bioavailability of molecular crystals: Tautomeric polymorphs of omeprazole. Mol. Pharm. 2011, 8, 1867–1876. [Google Scholar] [CrossRef] [PubMed]
- Sanphui, P.; Tothadi, S.; Ganguly, S.; Desiraju, G.R. Salt and cocrystals of sildenafil with dicarboxylic acids Solubility and pharmacokinetic advantage of the glutarate salt. Mol. Pharm. 2013, 10, 4687–4697. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.C.; Hou, H. Improving mechanical properties of caffeine and methyl gallate crystals by cocrystallization. Cryst. Growth Des. 2008, 8, 1575–1579. [Google Scholar] [CrossRef]
- Chow, S.F.; Chen, M.; Shi, L.; Chow, A.H.; Sun, C.C. Simultaneously improving the mechanical properties, dissolution performance, and hygroscopicity of ibuprofen and flurbiprofen by co-crystallization with nicotinamide. Pharm. Res. 2012, 29, 1854–1865. [Google Scholar] [CrossRef] [PubMed]
- Krishna, G.R.; Shi, L.; Bag, P.P.; Sun, C.C.; Reddy, C.M. Correlation among crystal structure, mechanical behavior, and tabletability in the co-crystals of vanillin isomers. Cryst. Growth Des. 2015, 15, 1827–1832. [Google Scholar] [CrossRef]
- Mishra, M.K.; Sanphui, P.; Ramamurty, U.; Desiraju, G.R. Solubility-Hardness correlation in molecular crystals: Curcumin and sulfathiazole polymorphs. Cryst. Growth Des. 2014, 14, 3054–3061. [Google Scholar] [CrossRef]
- Feng, Y.; Grant, D.J.W. Influence of crystal structure on the compaction properties of N-Alkyl 4-Hydrokxybenzoate Esters (Parabens). Pharm. Res. 2006, 23, 1608–1616. [Google Scholar] [CrossRef] [PubMed]
- Duncan-Hewitt, W.C.; Mount, D.L.; Yu, A. Hardness anisotropy of acetaminophen crystals. Pharm. Res. 1994, 11, 616–623. [Google Scholar] [CrossRef] [PubMed]
- Finnie, S.; Prasad, K.V.R.; Sheen, D.B.; Sherwood, J.N. Microhardness and dislocation identification studies on paracetamol single crystals. Pharm. Res. 2001, 18, 674–681. [Google Scholar] [CrossRef] [PubMed]
- Egart, M.; Ilić, I.; Janković, B.; Lah, N.; Srčič, S. Compaction properties of crystalline pharmaceutical ingredients according to the walker model and nanomechanical attributes. Int. J. Pharm. 2014, 472, 347–355. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Sheikh, A.Y.; Ho, R. Pharmaceutical ingredient crystals using nanoindentation and high-resolution total scattering pair distribution function analysis. J. Pharm. Sci. 2014, 103, 3879–3890. [Google Scholar] [CrossRef] [PubMed]
- Raut, D.; Kiran, M.S.R.N.; Mishra, M.K.; Asiri, B.M.; Ramamurty, U. On the loading rate sensitivity of plastic deformation in molecular crystals. CrystEngComm 2016, 18, 3551–3555. [Google Scholar] [CrossRef]
- Katz, J.M.; Buckner, I.S. Characterization of strain rate sensitivity in pharmaceutical materials using indentation creep analysis. Int. J. Pharm. 2013, 442, 13–19. [Google Scholar] [CrossRef] [PubMed]
- Kaupp, G.; Naimi-Jamal, M.R. Mechanically induced molecular migrations in molecular crystals. CrystEngComm 2005, 7, 402–410. [Google Scholar] [CrossRef]
- Varughese, S.; Kiran, M.S.R.N.; Ramamurty, U.; Desiraju, G.R. Nanoindentation as a probe for mechanically-induced molecular migration in layered organic donar-acceptor complexes. Chem. Asian J. 2012, 7, 2118–2125. [Google Scholar] [CrossRef] [PubMed]
- Jing, Y.; Zhang, Y.; Blendell, J.; Koslowski, M.; Carvajal, M.T. Nanoindentation method to study slip planes in molecular crystals in a systematic manner. Cryst. Growth Des. 2011, 11, 5260–5267. [Google Scholar] [CrossRef]
- Thakuria, R.; Eddleston, M.D.; Chow, E.H.H.; Taylor, L.J.; Aldous, B.J.; Krzyzaniak, J.F.; Jonesa, W. Use of In-Situ atomic force microscopy to follow phase changes at crystal surfaces in real time. CrystEngComm 2013, 52, 10541–10544. [Google Scholar]
- Roberts, R.J.; Rowe, R.C. The compaction of pharmaceutical and other model materials: A pragmatic approach. Chem. Eng. Sci. 1987, 42, 903–911. [Google Scholar] [CrossRef]
- Duncan-Hewitt, W.C.; Weatherly, G.C. Evaluating the hardness, young’s modulus and fracture toughness of some pharmaceutical crystals using microindentation techniques. J. Mater. Sci. Lett. 1989, 8, 1350–1352. [Google Scholar] [CrossRef]
- Munimunda, P.; Hintsala, E.A.S.; Mishra, M.K. Mechanical anisotropy and pressure induced structural changes in piroxicam crystals probed by in-situ indentation and Raman spectroscopy. JOM 2017, 69, 57–64. [Google Scholar] [CrossRef]
- Lei, L.; Carvajal, T.; Koslowski, M. Defect-induced solid state amorphization of molecular crystals. J. Appl. Phys. 2012, 111, 073505. [Google Scholar] [CrossRef]
- Boldyreva, E.V.; Sowa, H.; Ahsbahs, H.; Goryainov, S.V.; Chernyshev, V.V.; Dmitriev, V.P.; Seryotkin, Y.V.; Kolesnik, E.N.; Shakhtshneider, T.P.; Ivashevskaya, S.N.; et al. Pressure-Induced phase transitions in organic molecular crystals: A combination of x-ray single-crystal and powder diffraction Raman and IR-spectroscopy. J. Phys. Conf. Ser. 2008, 121, 022023. [Google Scholar] [CrossRef]
- Mohamed, R.M.; Mishra, M.K.; Al-Harbi, L.M.; Al-Ghamdi, M.S.; Ramamurty, U. Anisotropy in the mechanical properties of organic crystals: Temperature dependence. RSC Adv. 2015, 5, 64156–64162. [Google Scholar] [CrossRef]
- Mishra, M.K.; Ramamurty, U.; Desiraju, G.R. Bimodal nanoindentation response of the (0 0 1) face in crystalline sodium saccharin dehydrate. Macedonian J. Chem. Chem. Eng. 2015, 34, 51–55. [Google Scholar] [CrossRef]
- Kiran, M.S.R.N.; Varughese, S.; Ramamurty, U.; Desiraju, G.R. Effect of dehydration on the mechanical properties of sodium saccharin dihydrate probed with nanoindentation. CrystEngComm 2012, 14, 2489–2493. [Google Scholar] [CrossRef]
- Egart, M.; Jankovi, B.; Srcic, S. Application of instrumented nanoindentation in preformulation studies of pharmaceutical active ingredients and excipients. Acta Pharm. 2016, 66, 303–330. [Google Scholar] [CrossRef] [PubMed]
- Taylor, L.J.; Papadopoulos, D.G.; Dunn, P.J.; Bentham, A.C.; Dawson, N.J.; Mitchell, J.C.; Snowden, M.J. Predictive milling of pharmaceutical materials using nanoindentation of single crystals. Org. Proc. Res. Dev. 2004, 8, 674–679. [Google Scholar] [CrossRef]
- Cao, X.; Morganti, M.; Hancock, B.C.; Masterson, V.M. Correlating particle hardness with powder compaction performance. J. Pharm. Sci. 2010, 99, 4307–4316. [Google Scholar] [CrossRef] [PubMed]
- Masterson, V.M.; Cao, X. Evaluating particle hardness of pharmaceutical solids using AFM nanoindentation. Int. J. Pharm. 2008, 362, 163–171. [Google Scholar] [CrossRef] [PubMed]
- Munz, D.; Bubsey, R.T.; Shannon, J.L., Jr. Fracture toughness determination of Al2O3 using fourpointbend specimens with straightthrough and chevron notches. J. Am. Ceram. Soc. 1980, 63, 300–305. [Google Scholar] [CrossRef]
- Ritchie, R.O.; Dauskardt, R.H.; Yu, W.; Brendzel, A.M. Cyclic fatiguecrack propagation, stresscorrosion, and fracturetoughness behavior in pyrolytic carboncoated graphite for prosthetic heart valve applications. J. Biomed. Mater. Res. 1990, 24, 89–206. [Google Scholar] [CrossRef] [PubMed]
- Fett, T.; Munz, D. Influence of narrow starter notches on the initial crack growth resistance curve of ceramics. Arch. Appl. Mech. 2006, 76, 667–679. [Google Scholar] [CrossRef]
- Lawn, B.R.; Evans, A.G.; Marshall, D.B. Elastic/Plastic indentation damage in ceramics: The median/radial crack system. J. Am. Ceram. Soc. 1980, 63, 574–581. [Google Scholar] [CrossRef]
- Anstis, G.R.; Chantikul, P.; Lawn, B.R.; Marshall, D.B. A critical evaluation of indentation techniques for measuring fracture toughness: I, direct crack measurements. J. Am. Ceram. Soc. 1981, 64, 533–538. [Google Scholar] [CrossRef]
- Fett, T.; Kounga, A.B.; Rodel, J. Stresses and stress intensity factor from cod of vickers indentation cracks. J. Mater. Sci. 2004, 39, 2219–2221. [Google Scholar] [CrossRef]
- Fett, T.; Njiwa, A.B.K.; Rodel, J. Crack opening displacements of vickers indentation cracks. Eng. Fract. Mech. 2005, 72, 647–659. [Google Scholar] [CrossRef]
- Lawn, B. Indentation fracture: Applications in the assessment of strength of ceramics. J. Aust. Ceram. Soc. 1980, 16, 4. [Google Scholar]
- Harding, D.S.; Oliver, W.C.; Pharr, G.M. Cracking during nanoindentation and its use in the measurement of fracture toughness. Mater. Res. Soc. Symp. Proc. 1995, 356, 663–668. [Google Scholar] [CrossRef]
- Lawn, B.R.; Marshall, D.B. Hardness, toughness, and brittleness: An indentation analysis. J. Am. Ceram. Soc. 1979, 62, 347–350. [Google Scholar] [CrossRef]
- Duncan-Hewitt, W.C.; Weatherly, G. Evaluating the fracture toughness of sucrose crystals using microindentation techniques. Pharm. Res. 1989, 6, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Duncan-Hewitt, W.C.; Weatherly, G. Evaluating the deformation kinetics of sucrose crystals using microindentation techniques. Pharm. Res. 1989, 6, 1060–1066. [Google Scholar] [CrossRef] [PubMed]
- Prasad, K.V.R.; Sheen, D.B.; Sherwood, J.N. Fracture property studies of paracetamol single crystals using microindentation techniques. Pharm. Res. 2001, 18, 867–872. [Google Scholar] [CrossRef] [PubMed]
- Mishra, M.K.; Ramamurty, U.; Desiraju, G.R. Mechanical property design of molecular crystals. Curr. Opin. Solid State Mater. Sci. 2016, 20, 361–370. [Google Scholar] [CrossRef]
- Chung, Y.W.; Sproul, W.D. Super hard coating materials. MRS Bull. 2003, 28, 164–165. [Google Scholar] [CrossRef]
- Mishra, K.; Verma, D.; Bysakh, S.; Pathak, L.C. Hard and soft multilayered sicn nanocoatings with high hardness and toughness. J. Nanomater. 2013. [Google Scholar] [CrossRef]
- Berding, M.A.; Sher, A.; van Shilfgaarde, M.; Chen, A.B. Fracture and Hardness Characteristics of Semiconductor Alloys. Available online: http://www.dtic.mil/dtic/tr/fulltext/u2/a204807.pdf (accessed on 23 September 2017).
- Louzguine-Luzgin, D.V.; Louzguina-Luzgina, L.V.; Churyumov, A.Y. Mechanical properties and deformation behavior of bulk metallic glasses. Metals 2013, 3, 1–22. [Google Scholar] [CrossRef]
- Tan, J.C.; Cheetham, A.K. Mechanical properties of hybrid inorganic-organic framework materials: Establishing fundamental structure-property relationships. Chem. Soc. Rev. 2011, 40, 1059–1080. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Novikov, N.V. Innovative Superhard Materials and Sustainable Coatings for Advanced Manufacturing. Available online: https://link.springer.com/book/10.1007/1-4020-3471-7?page=2 (accessed on 24 September 2017).
- Marinescu, I.D.; Tönshoff, H.K.; Inasaki, I. Handbook of Ceramic Grinding and Polishing; William Andrew Publishing: Norwich, NY, USA, 2000. [Google Scholar]
- Kutz, M. Handbook of Materials Selection; John Wiley and Sons: Hoboken, NJ, USA, 2002; pp. 384–424. [Google Scholar]
- Chen, C.P. Analytical Determination of Critical Crack Size in Solar Cells. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19880017352.pdf (accessed on 23 September 2017).
- Chapter 3: Nanoindentation-Induced Mechanical Responses. Available online: https://ir.nctu.edu.tw/bitstream/11536/78079/5/180105.pdf (accessed on 23 September 2017).
- Xu, J.; Ramamurty, U.; Ma, E. The fracture toughness of Bulk metallic glasses. JOM 2010, 62, 10–18. [Google Scholar] [CrossRef]
- Subhash, G.; Koepper, B.J.; Chandra, A. Dynamic indentation hardness and rate sensitivity in metals. J. Eng. Mater. Technol. 1999, 121, 257–263. [Google Scholar] [CrossRef]
- Mason, J.K.; Lund, A.C.; Schuh, C.A. Determining the Activation Energy and Volume for the onset of Plasticity during Nanoindentation. Phys. Rev. B 2006, 73, 1–14. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Singh, G.; Prasad, K.E.; Narasimhan, R.; Ramamurty, U. On the strain rate sensitivity of plastic flow in metallic glasses mater. Sci. Eng. A 2015, 625, 245–251. [Google Scholar] [CrossRef]
- Golbe, D.L.; Wolff, E.G. Strain-rate sensitivity index of thermoplastics. J. Mater. Sci. 1993, 23, 5986–5994. [Google Scholar]
- Song, J.M.; Shen, Y.L.; Su, C.W.; Lai, Y.S.; Chiu, Y. Strain rate dependence on nanoindentation responses of interfacial intermetallic compounds in electronic solder joints with cu and ag substrates. Mater. Trans. 2009, 50, 1231–1234. [Google Scholar] [CrossRef]
- Bradby, J.E.; Williams, J.S.; Wong-Leung, J.; Swain, M.V.; Munroe, P. Transmission electron microscopy observation of deformation microstructure under spherical indentation in silicon. Appl. Phys. Lett. 2000, 77, 3749–3751. [Google Scholar] [CrossRef]
- Bradby, J.E.; Williams, J.S.; Wong-Leung, J.; Swain, M.V.; Munroe, P. Mechanical deformation of InP and GaAs by spherical indentation. Appl. Phys. Lett. 2001, 78, 3235–3237. [Google Scholar] [CrossRef]
- Bradby, J.E.; Williams, J.S.; Wong-Leung, J.; Swain, M.V.; Munroe, P. Nanoindentation-Induced deformation of Ge. Appl. Phys. Lett. 2002, 80, 2651–2653. [Google Scholar] [CrossRef]
- Kiran, M.S.R.N.; Tran, T.T.; Smillie, L.A.; Haberl, B.; Subianto, D.; Williams, J.S.; Bradby, J.E. Temperature-dependent mechanical deformation of silicon at the nanoscale: Phase transformation versus defect propagation. J. Appl. Phys. 2015, 117, 205901. [Google Scholar] [CrossRef]
























| Plane | (011) | (001) | (120) |
|---|---|---|---|
| Indentation direction | [016] | [001] | [810] |
| Slip plane | (010) | (010) | (010) |
| Slip direction | [001] | [001] | [100] |
| Schmid factor | 0.48 | 0.35 | 0.24 |
| Hardness (Mpa) | 275 ± 12 | 340 ± 7 | 410 ± 11 |
| 2-D layers arranged (°) with respect to indentation plane | 22 | 90 | 12 |
| Sulfathiazole Polymorphs | Major Face | Slip Direction | Schmid Factor | H (GPa) | Angle (Degree) between the Trace of the Molecular Layer and the Indentation Direction |
|---|---|---|---|---|---|
| Form 1 | (100) | [102] | 0.468 | 0.356 ± 0.010 | 145.3 |
| Form II | (100) | [102] | 0.039 | 1.080 ± 0.015 | 92.3 |
| Form III | (100) | [001] | 0.089 | 0.704 ± 0.018 | 95.1 |
| Form IV | (10) | [001] | 0.043 | 0.881 ± 0.012 | 92.5 |
| S. No | Crystal | Crystal Face | Type of Tip Used | Hardness, H (GPa) | Reference |
|---|---|---|---|---|---|
| 1 | 1,1-Diamino2,2-dinitroethylene | (0 2 0) | Berkovich | 0.52 ± 0.05 | [86] |
| (−1 0 1) | -do- | 0.63 ± 0.02 | [86] | ||
| (0 0 2) | -do- | 0.67 ± 0.03 | [86] | ||
| 2 | Saccharin | (1 0 0) | Zircon Berkovich tip | 0.530 ± 3.0 | [116] |
| (0 1 1) | -do- | 0.501 ± 2.3 | [116] | ||
| (1 0 0) | A cube-corner indenter | 0.610 ± 0.01 | [85] | ||
| (0 1 1) | A cube-corner indenter | 0.550 ± 0.02 | [85] | ||
| 3 | L-alanine | (0 0 1) | -do- | 0.114 ± 4.8 | [116] |
| (1 0 1) | -do- | 0.943 ± 3.1 | [116] | ||
| 4 | BF2dbm(Bu)2 | (0 0 1) | Berkovich | 0.092 ± 4.04 | [98] |
| 5 | BF2dbm(OMe)2 | (0 1 0) | Berkovich | 0.264 ± 10.8 | [98] |
| 6 | BF2dbm(OMe) | (0 0 1) | Berkovich | 0.255 ± 8.48 | [98] |
| 7 | Sodium Saccharin dihydrate crystals | (0 0 1) | Berkovich | 1.20 ± 0.04 | [117] |
| (0 0 1) | -do- | 0.78 ± 0.03 | [116] | ||
| (0 1 1) | -do- | 0.662 ± 0.02 | [118] | ||
| (1 0 1) | -do- | 0.716 ± 0.02 | [118] | ||
| 8 | Piroxicam form-1 | (−1 0 0) | -do- | 0.56 ± 0.18 | [2,119] |
| (0 1 1) | -do- | 0.67 ± 0.04 | [2,119] | ||
| (0 1 −1) | -do- | 0.42 ± 0.02 | [2,119] | ||
| 9 | Famotidine form A | (−1 0 0) | -do- | 1.58 ± 0.4 | [2,119] |
| (0 0 −1) | -do- | 1.35 ± 0.16 | [2,119] | ||
| 10 | Famotidine form B | (−1 0 1) | -do- | 0.84 ± 0.16 | [2,119] |
| 11 | Nifedipineα-form | (1 0 0) | -do- | 0.71 ± 0.61 | [2,119] |
| 12 | Olanzapine form 1 | (1 0 0) | -do- | 0.74 ± 0.04 | [2,119] |
| (0 −1 −1) | -do- | 0.72 ± 0.02 | [2,119] | ||
| 13 | Aspirin polymorph-1 | (1 0 0) | -do- | 0.257 ± 0.007 | [89] |
| (0 0 ) | -do- | 0.240 ± 0.008 | [89] | ||
| (0 0 1) | -do- | 0.10 | [90] | ||
| (1 0 0) | -do- | 0.12 | [90] | ||
| 14 | Aspirin polymorph-2 | (1 0 ) | -do- | 0.152 ± 0.004 | [89] |
| 15 | Sildenafil Citrate | ---- | -do- | 0.52 ± 0.06 | [120] |
| 16 | Voriconazole | ---- | -do- | 0.13 ± 0.01 | [120] |
| 17 | Sucrose | (1 0 0) | -do- | 1.62 ± 0.17 | [90] |
| (0 0 1) | -do- | 1.57 ± 0.07 | [86] | ||
| ---- | -do- | 2.3 ± 0..4 | [121] | ||
| ---- | Diamond tip | 2 ± 0.5 | [122] | ||
| 18 | Lactose | ---- | Diamond tip | 0.43 ± 0.08 | [122] |
| 19 | Absorbic Acid | ---- | Diamond tip | 5.6 ± 1.8 | [122] |
| 20 | TATB | (0 0 1) | Berkovich | 1.02 ± 0.09 | [87] |
| 21 | α-RDX | (2 1 0) | -do- | 0.672 ± 0.035 | [87] |
| (2 1 0) | -do- | 0.798 ± 0.030 | [87] | ||
| (2 1 0) | -do- | 1.06 | [87] | ||
| (0 2 1) | -do- | 0.681 ± 0.033 | [87] | ||
| (0 0 1) | -do- | 0.615 ± 0.035 | [87] | ||
| (0 0 1) | -do- | 1.05 | [87] | ||
| ---- | -do- | 0.74 ± 0.09 | [88] | ||
| (0 2 1) | -do- | 0.681 | [88] | ||
| (2 1 0) | -do- | 0.798 | [88] | ||
| Multiple | -do- | 0.74 | [88] | ||
| 22 | β-HMX | (0 1 0) | -do- | 1.13 ± 0.045 | [87] |
| (0 1 0) | -do- | 0.65 ± 0.09 | [87] | ||
| 23 | HMX | ---- | -do- | 0.95 | [88] |
| (0 1 0) | -do- | 0.65 | [88] | ||
| -do- | 0.99 ± 0.06 | [88] | |||
| 24 | LIM-105 | (0 1 0) | -do- | 0.72 ± 0.10 | [87] |
| 25 | Acetaminophen | (0 1 1) | -do- | 0.875 ± 0.029 | [87] |
| 26 | VOR | (1 0 0) | -do- | 0.366 ± 2.8 | [93] |
| 27 | VOR-HCl | (0 1 1 ) | -do- | 0.870 ± 6.0 | [93] |
| 28 | VOR-OXA1 | (0 1 0) | -do- | 0.426 ± 5.8 | [93] |
| 29 | VOR-OXA2 | (1 0 0) | -do- | 0.628 ± 2.0 | [93] |
| 30 | VOR-FUM | (1 0 0) | -do- | 0.292 ± 3.4 | [93] |
| 31 | VOR-PAB | (1 0 0) | -do- | 0.264 ± 5.0 | [93] |
| 32 | VOR-PHB | (1 0 0) | -do- | 0.262 ± 1.6 | [93] |
| 33 | Ibuprofen Lot A | ---- | -do- | 0.6 ± 0.1 | [121] |
| 34 | Ibuprofen Lot B | ---- | -do- | 0.4 ± 0.1 | [121] |
| 35 | Ibuprofen Lot C | ---- | -do- | 0.22 ± 0.04 | [121] |
| 36 | UK-370106 | ---- | -do- | 0.4 ± 0.1 | [121] |
| 37 | Acetaminophen | ---- | -do- | 1.0 ± 0.2 | [121] |
| 38 | Phenacetin | ---- | -do- | 0.9 ± 0.2 | [121] |
| 39 | PHA-739521 | ---- | -do- | 1.1 ± 0.1 | [121] |
| 40 | MCC | ---- | -do- | 1.4 ± 0.3 | [121] |
| 41 | Fluconazole | ---- | -do- | 2.0 ± 0.3 | [121] |
| 42 | TATB | (0 0 1) | -do- | 0.48 | [88] |
| ---- | 0.41 ± 0.04 | ||||
| 43 | TNT/CL-20 | ---- | 0.63 ± 0.13 | ||
| 44 | FOX-7 | (0 2 0) | 0.52 | ||
| 0 1) | 0.63 | ||||
| (0 0 2) | 0.67 | ||||
| ---- | 0.86 ± 0.08 | ||||
| 46 | ADAAF | ---- | 0.23 | ||
| (2 1 0) | 0.672 | ||||
| (0 0 1) | 0.615 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mannepalli, S.; Mangalampalli, K.S.R.N. Indentation Plasticity and Fracture Studies of Organic Crystals. Crystals 2017, 7, 324. https://doi.org/10.3390/cryst7110324
Mannepalli S, Mangalampalli KSRN. Indentation Plasticity and Fracture Studies of Organic Crystals. Crystals. 2017; 7(11):324. https://doi.org/10.3390/cryst7110324
Chicago/Turabian StyleMannepalli, Sowjanya, and Kiran S. R. N. Mangalampalli. 2017. "Indentation Plasticity and Fracture Studies of Organic Crystals" Crystals 7, no. 11: 324. https://doi.org/10.3390/cryst7110324
APA StyleMannepalli, S., & Mangalampalli, K. S. R. N. (2017). Indentation Plasticity and Fracture Studies of Organic Crystals. Crystals, 7(11), 324. https://doi.org/10.3390/cryst7110324