A 130 GHz Electro-Optic Ring Modulator with Double-Layer Graphene
Abstract
:1. Introduction
2. Principle of Operation
3. Relative Index of Graphene
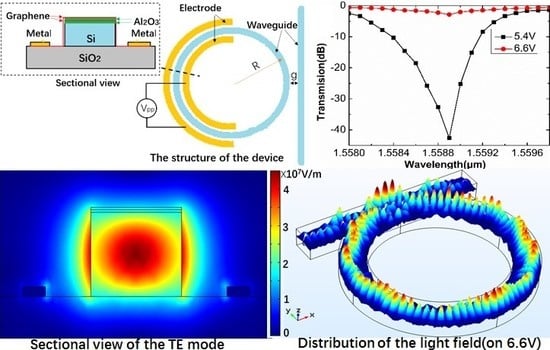
4. Numerical Simulations and Optimization
- With dielectric graphene (ng = 1.332 + i0.105, voltage = 5.4 V) neff = 2.2755 − i6.2283 × 10−5
- With metallic graphene (ng = 0.174 + i1.672, voltage = 6.6 V) neff = 2.2756 − i4.3248 × 10−3
5. Estimation of Modulation Speed and Energy Required
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, L.; Preston, K.; Manipatruni, S.; Lipson, M. Integrated GHz silicon photonic interconnect with micrometer-scale modulators and detectors. Opt. Express 2009, 17, 15248–15256. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Liu, Y.; Liu, E. The Effect and Application on Plasma Dispersion of Si. Acta Photonica Sineca 1996, 25, 413–416. (In Chinese) [Google Scholar]
- Jiang, Y.; Jiang, W.; Gu, L.; Chen, X.; Chen, R.T. 80-micron interaction length silicon photonic crystal waveguide modulator. Appl. Phys. Lett. 2005, 87, 221105. [Google Scholar] [CrossRef]
- Alferness, R.C. Waveguide Electrooptic Modulators. IEEE Trans. Microw. Theory Tech. 1982, 30, 1121–1137. [Google Scholar] [CrossRef]
- Treyz, G.V.; May, P.G.; Halbout, J. Silicon Mach–Zehnder waveguide interferometers based on the plasma dispersion effect. Appl. Phys. Lett. 1991, 59, 771–773. [Google Scholar] [CrossRef]
- Capmany, J.; Novak, D. Microwave photonics combines two worlds. Nat. Photonics 2007, 1, 319–330. [Google Scholar] [CrossRef]
- Green, W.M.; Rooks, M.J.; Sekaric, L.; Vlasov, Y.A. Ultra-compact, low RF power, 10 Gb/s silicon Mach-Zehnder modulator. Opt. Express 2007, 15, 17106–17113. [Google Scholar] [CrossRef] [PubMed]
- Bogaerts, W.; Heyn, P.D.; Vaerenbergh, T.V.; de Vos, K.; Selvaraja, S.K.; Claes, T.; Dumon, P.; Bienstman, P.; Van Thourhout, D.; Baets, R. Silicon microring resonators. Laser Photonics Rev. 2012, 6, 47–73. [Google Scholar] [CrossRef]
- Xu, Q.; Manipatruni, S.; Schmidt, B.; Shakya, J.; Lipson, M. 12.5 Gbit/s carrier-injection-based silicon micro-ring silicon modulators. Opt. Express 2007, 15, 430–436. [Google Scholar] [CrossRef] [PubMed]
- Azawa, H.; Kuo, Y.H.; Dunayevskiy, I.; Luo, J.; Jen, A.K.-Y.; Fetterman, H.R. Ring resonator-based electrooptic polymer traveling-wave modulator. Lightwave Technol. J. 2006, 24, 3514–3519. [Google Scholar]
- Chen, L.; Xu, Q.; Wood, M.G.; Reano, R.M. Hybrid silicon and lithium niobate electro-optical ring modulator. Optica 2014, 1, 112–118. [Google Scholar] [CrossRef]
- Phatak, A.; Cheng, Z.; Qin, C.; Goda, Q. Design of electro-optic modulators based on graphene-on-silicon slot waveguides. Opt. Lett. 2016, 41, 2501. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.Q.; Cheng, Z.; Shu, C.; Tsang, H.K. Optical Absorption in Graphene-on-Silicon Nitride Microring Resonators. IEEE Photonics Technol. Lett. 2015, 27, 1765–1767. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, Z.; Chen, Z.; Chen, Z.; Wan, X.; Zhu, B.; Tsang, H.K.; Shu, C.; Xu, J.B. High-responsivity graphene-on-silicon slot waveguide photodetectors. Nanoscale 2016, 8, 13206. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Yin, X.; Ulinavila, E.; Geng, B.; Zentgraf, T.; Ju, L.; Wang, F.; Zhang, X. A graphene-based broadband optical modulator. Nature 2011, 474, 64–67. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Yin, X.; Zhang, X. Double-Layer Graphene Optical Modulator. Nano Lett. 2014, 12, 1482–1485. [Google Scholar] [CrossRef] [PubMed]
- Koester, S.J.; Li, M. High-speed waveguide-coupled graphene-on-graphene optical modulators. Appl. Phys. Lett. 2012, 100, 171107. [Google Scholar] [CrossRef]
- Lu, Z.; Zhao, W. Nanoscale electro-optic modulators based on graphene-slot waveguides. J. Opt. Soc. Am. B 2012, 29, 1490–1496. [Google Scholar] [CrossRef]
- Gosciniak, J.; Tan, D.T. Theoretical investigation of graphene-based photonic modulators. Sci. Rep. 2013, 3, 1897. [Google Scholar] [CrossRef] [PubMed]
- Mohsin, M.; Schall, D.; Otto, M.; Noculak, A.; Neumaier, D.; Kurz, H. Graphene based low insertion loss electro-absorption modulator on SOI waveguide. Opt. Express 2014, 22, 15292–15297. [Google Scholar] [CrossRef] [PubMed]
- Phare, C.T.; Lee, Y.H.D.; Cardenas, J.; Lipson, M. Graphene electro-optic modulator with 30 GHz bandwidth. Nat. Photonics 2015, 9, 511–514. [Google Scholar] [CrossRef]
- Du, W.; Li, E.P.; Hao, R. Tunability Analysis of a Graphene-Embedded Ring Modulator. IEEE Photonics Technol. Lett. 2014, 26, 2008–2011. [Google Scholar] [CrossRef]
- Midrio, M.; Boscolo, S.; Moresco, M.; Romagnoli, M.; De Angelis, C.; Locatelli, A.; Capobianco, A.D. Graphene-assisted critically-coupled optical ring modulator. Opt. Express 2012, 20, 23144–23155. [Google Scholar] [CrossRef] [PubMed]
- Yariv, A. Critical coupling and its control in optical waveguide-ring resonator systems. IEEE Photonics Technol. Lett. 2002, 14, 483–485. [Google Scholar] [CrossRef]
- Bao, Q.; Zhang, H.; Wang, Y.; Ni, Z.; Yan, Y.; Shen, Z.X.; Loh, K.P.; Tang, D.Y. Atomic-Layer Graphene as a Saturable Absorber for Ultrafast Pulsed Lasers. Adv. Funct. Mater. 2009, 19, 3077–3083. [Google Scholar] [CrossRef]
- Fang, T.; Konar, A.; Xing, H.; Jena, D. Carrier Statistics and Quantum Capacitance of Graphene Sheets and Ribbons. Physics 2007, 91, 092109. [Google Scholar]
- Xia, F.; Perebeinos, V.; Lin, Y.M.; Wu, Y.; Avouris, P. The origins and limits of metal-graphene junction resistance. Nat. Nanotechnol. 2011, 6, 179–184. [Google Scholar] [CrossRef] [PubMed]
- Datta, S. Electronic Transport in Mesoscopic Systems; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Smith, J.T.; Franklin, A.D.; Farmer, D.B.; Dimitrakopoulos, C.D. Reducing contact resistance in graphene devices through contact area patterning. ACS Nano 2013, 7, 3661–3667. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Wei, J.; Sun, X.; Yu, H. A Study on Graphene-Metal Contact. Crystals 2013, 3, 257–274. [Google Scholar] [CrossRef]
- Leong, W.S.; Gong, H.; Thong, J.T. Low-contact-resistance graphene devices with nickel-etched-graphene contacts. ACS Nano 2013, 8, 994–1001. [Google Scholar] [CrossRef] [PubMed]










© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Liu, H.; Li, J.; Wang, S.; Qu, S.; Dong, L. A 130 GHz Electro-Optic Ring Modulator with Double-Layer Graphene. Crystals 2017, 7, 65. https://doi.org/10.3390/cryst7030065
Wu L, Liu H, Li J, Wang S, Qu S, Dong L. A 130 GHz Electro-Optic Ring Modulator with Double-Layer Graphene. Crystals. 2017; 7(3):65. https://doi.org/10.3390/cryst7030065
Chicago/Turabian StyleWu, Lei, Hongxia Liu, Jiabin Li, Shulong Wang, Sheng Qu, and Lu Dong. 2017. "A 130 GHz Electro-Optic Ring Modulator with Double-Layer Graphene" Crystals 7, no. 3: 65. https://doi.org/10.3390/cryst7030065
APA StyleWu, L., Liu, H., Li, J., Wang, S., Qu, S., & Dong, L. (2017). A 130 GHz Electro-Optic Ring Modulator with Double-Layer Graphene. Crystals, 7(3), 65. https://doi.org/10.3390/cryst7030065