Interfacial Mixing Analysis for Strained Layer Superlattices by Atom Probe Tomography
Abstract
:1. Introduction
2. Materials and Methods
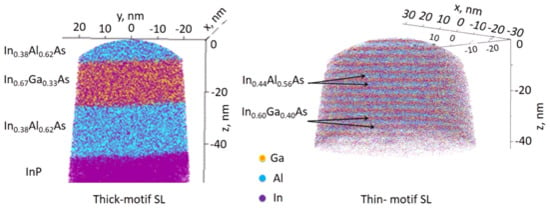
3. Results
4. Discussion
4.1. Extent of Interfacial Mixing in the Thick-Motif Sample
4.2. Extent of Interfacial Mixing in the Thin-Motif Sample
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Botez, D.; Kirch, J.D.; Chang, C.; Boyle, C.; Kim, H.; Oresick, K.M.; Sigler, C.; Mawst, L.J.; Jo, M.; Shin, J.C.; et al. High internal differential efficiency mid-infrared quantum cascade lasers. Proc. SPIE 2017, 10123, 101230Q. [Google Scholar]
- Wang, C.A.; Schwarz, B.; Siriani, D.F.; Connors, M.K.; Missaggia, L.J.; Calawa, D.R.; McNulty, D.; Akey, A.; Zheng, M.C.; Donnelly, J.P.; et al. Sensitivity of heterointerfaces on emission wavelength of quantum cascade lasers. J. Cryst. Growth 2017, 464, 215–220. [Google Scholar] [CrossRef]
- Wood, A.W.; Guan, Y.; Forghani, K.; Anand, A.; Kuech, T.F.; Babcock, S.E. Unexpected bismuth concentration profiles in metal-organic vapor phase epitaxy-grown Ga(As1−xBix)/GaAs superlattices revealed by Z-contrast scanning transmission electron microscopy imaging. APL Mater. 2015, 3, 036108. [Google Scholar] [CrossRef]
- Rajeev, A.; Mawst, L.J.; Kirch, J.D.; Botez, D.; Miao, J.; Buelow, P.; Kuech, T.F.; Li, X.; Sigler, C.; Babcock, S.E.; et al. Regrowth of quantum cascade laser active regions on metamorphic buffer layers. J. Cryst. Growth 2016, 452, 268–271. [Google Scholar] [CrossRef]
- Gault, B.; Moody, M.P.; Cairney, J.M.; Ringer, S.P. Atom Probe Microscopy; Springer: New York, NY, USA, 2012. [Google Scholar]
- CAMECA IVAS. Available online: http://www.cameca.com/service/software/ivas (accessed on 1 August 2018).
- Vurpillot, F.; da Costa, G.; Menand, A.; Blavette, D. Structural analyses in three-dimensional atom probe: A Fourier transform approach. J. Microsc. 2001, 203, 295–302. [Google Scholar] [CrossRef] [PubMed]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Oxford University Press: Bristol, UK, 1975. [Google Scholar]
- Pantzas, K.; Beaudoin, G.; Patriarche, G.; Largeau, L.; Mauguin, O.; Pegolotti, G.; Vasanelli, A.; Calvar, A.; Amanti, M.; Sirtori, C.; et al. Sub-nanometrically resolved chemical mappings of quantum-cascade laser active regions. Semicond. Sci. Technol. 2016, 31, 055017. [Google Scholar] [CrossRef]
- Offermans, P.; Koenraad, P.M.; Wolter, J.H.; Beck, M.; Aellen, T.; Faist, J. Digital alloy interface grading of an InAlAs/InGaAs quantum cascade laser structure studied by cross-sectional scanning tunneling microscopy. Appl. Phys. Lett. 2003, 83, 4131–4133. [Google Scholar] [CrossRef] [Green Version]
- Marmalyuk, A.A.; Govorkov, O.I.; Petrovsky, A.V.; Nikitin, D.B.; Padalitsa, A.A.; Bulaev, P.V.; Budkin, I.V.; Zalevsky, I.D. Investigation of indium segregation in InGaAs/(Al)GaAs quantum wells grown by MOCVD. 2002, 237–239, 264–268. [Google Scholar] [CrossRef]
- Botez, D.; Kirch, J.D.; Boyle, C.; Oresick, K.M.; Sigler, C.; Kim, H.; Knipfer, B.B.; Ryu, J.H.; Lindberg, D., III; Earles, T.; et al. High-efficiency, high-power mid-infrared quantum cascade lasers. Opt. Mater. Express 2018, 8, 1378–1398. [Google Scholar] [CrossRef]
- Seo, K.S.; Bhattacharya, P.K.; Kothiyal, G.P.; Hong, S. Interdiffusion and wavelength modification in In0.53Ga0.47As/In0.52Al0.48As quantum wells by lamp annealing. Appl. Phys. Lett. 1986, 49, 966–968. [Google Scholar] [CrossRef]
- Megalini, L.; Bonef, B.; Cabinian, B.C.; Zhao, H.; Taylor, A.; Speck, J.S.; Bowers, J.E.; Klamkin, J. 1550-nm InGaAsP multi-quantum-well structures selectively grown on v-groove-patterned SOI substrates. Appl. Phys. Lett. 2017, 111, 032105. [Google Scholar] [CrossRef]
- Liu, F.; Huang, L.; Davis, R.F.; Porter, L.M.; Schreiber, D.K.; Kuchibatla, S.V.N.; Shutthanandan, V.; Thevuthasan, S.; Preble, E.A.; Paskova, T.; et al. Composition and interface analysis of InGaN/GaN multiquantum-wells on GaN substrates using atom probe tomography. J. Vac. Sci. Technol. B 2014, 32, 051209. [Google Scholar] [CrossRef]





| Material | V:III Precursor Ratio | Growth Rate (nm/s) |
|---|---|---|
| Thick-motif SL | ||
| In0.37Al0.63As | 428 | 0.10 |
| In0.67Ga0.33As | 315 | 0.14 |
| Thin-motif SL | ||
| In0.44Al0.56As | 375 | 0.12 |
| In0.60Ga0.40As | 387 | 0.11 |
| HRXRD Composition; Period | APT Composition; Period | |
|---|---|---|
| Thick-motif SL | In0.37Al0.63As/In0.67Ga0.33As; 43.5 nm | In0.38Al0.62As/In0.69Ga0.31As; 38.6 nm |
| Thin-motif SL | In0.44Al0.56As/In0.60Ga0.40As; 4.1 nm | In0.46Al0.50Ga0.04As/In0.58Ga0.31Al0.11As; 3.7 nm |
| Interface | Diffusion Length (nm) for Al | Diffusion Length (nm) for Ga |
|---|---|---|
| InAlAs–InGaAs | 0.52 ± 0.02 | 0.54 ± 0.04 |
| InGaAs–InAlAs | 0.51 ± 0.02 | 0.58 ± 0.03 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rajeev, A.; Chen, W.; Kirch, J.D.; Babcock, S.E.; Kuech, T.F.; Earles, T.; Mawst, L.J. Interfacial Mixing Analysis for Strained Layer Superlattices by Atom Probe Tomography. Crystals 2018, 8, 437. https://doi.org/10.3390/cryst8110437
Rajeev A, Chen W, Kirch JD, Babcock SE, Kuech TF, Earles T, Mawst LJ. Interfacial Mixing Analysis for Strained Layer Superlattices by Atom Probe Tomography. Crystals. 2018; 8(11):437. https://doi.org/10.3390/cryst8110437
Chicago/Turabian StyleRajeev, Ayushi, Weixin Chen, Jeremy D. Kirch, Susan E. Babcock, Thomas F. Kuech, Thomas Earles, and Luke J. Mawst. 2018. "Interfacial Mixing Analysis for Strained Layer Superlattices by Atom Probe Tomography" Crystals 8, no. 11: 437. https://doi.org/10.3390/cryst8110437
APA StyleRajeev, A., Chen, W., Kirch, J. D., Babcock, S. E., Kuech, T. F., Earles, T., & Mawst, L. J. (2018). Interfacial Mixing Analysis for Strained Layer Superlattices by Atom Probe Tomography. Crystals, 8(11), 437. https://doi.org/10.3390/cryst8110437