Molecular Dynamics Simulation of Nanoscale Abrasive Wear of Polycrystalline Silicon
Abstract
:1. Introduction
2. Simulation Details
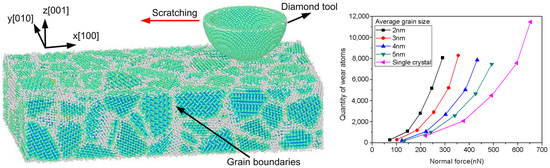
3. Results and Discussion
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Maboudian, R.; Ashurst, W.R.; Carraro, C. Tribological challenges in micromechanical systems. Tribol. Lett. 2002, 12, 95–100. [Google Scholar] [CrossRef]
- Flater, E.E.; Corwin, A.D.; de Boer, M.P.; Carpick, R.W. In-situ wear studies of surface micromachined interfaces subject to controlled loading. Wear 2006, 260, 580–593. [Google Scholar] [CrossRef]
- de Boer, M.P.; Mayer, T.M. Tribology of MEMS. MRS Bull. 2001, 26, 302–304. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and Rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Gotsmann, B.; Lantz, M. Atomistic Wear in a Single Asperity Sliding Contact. Phys. Rev. Lett. 2008, 101, 125501. [Google Scholar] [CrossRef] [PubMed]
- Bhaskaran, H.; Gotsmann, B.; Sebastian, A.; Drechsler, U.; Lantz, M.A.; Despont, M.; Jaroenapibal, P.; Carpick, R.W.; Chen, Y.; Sridharan, K. Ultralow Nanoscale Wear through Atom-by-Atom Attrition in Silicon-containing Diamond-like Carbon. Nat. Nanotechnol. 2010, 5, 181–185. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, T.; Carpick, R.W. Nanoscale Wear as a Stress-Assisted Chemical Reaction. Nat. Nanotechnol. 2013, 8, 108–112. [Google Scholar] [CrossRef] [PubMed]
- Chung, K.-H.; Lee, Y.-H.; Kim, D.-E. Characteristics of fracture during the approach process and wear mechanism of a silicon AFM tip. Ultramicroscopy 2005, 102, 161–171. [Google Scholar] [CrossRef] [PubMed]
- Chung, K.H.; Kim, D.E. Fundamental investigation of micro wear rate using an atomic force microscope. Tribol. Lett. 2003, 15, 135–144. [Google Scholar] [CrossRef]
- Liu, J.; Notbohm, J.K.; Carpick, R.W.; Turner, K.T. Method for characterizing nanoscale wear of atomic force microscope tips. ACS Nano 2010, 4, 3763–3772. [Google Scholar] [CrossRef]
- Alsem, D.H.; Stach, E.A.; Dugger, M.T.; Enachescu, M.; Ritchie, R.O. An electron microscopy study of wear in polysilicon microelectromechanicalsystems in ambient air. Thin Solid Films 2007, 515, 3259–3266. [Google Scholar] [CrossRef]
- Alsem, D.H.; vander Hulst, R.; Stach, E.A.; Dugger, M.T.; De Hosson, J.T.M.; Ritchie, R.O. Wear mechanisms and friction parameters for sliding wear of micron-scale polysilicon sidewalls. Sens. Actuators A Phys. 2010, 163, 373–382. [Google Scholar] [CrossRef]
- Bhushan, B. Tribology on the macroscale to nanoscale of microelectromechanical system materials: A review. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2001, 215, 1–18. [Google Scholar] [CrossRef]
- Sundararajan, S.; Bhushan, B. Micro/nanotribological studies of polysilicon and SiC films for MEMS applications. Wear 1998, 217, 251–261. [Google Scholar] [CrossRef]
- Chung, K.H.; Jang, C.E.; Kim, D.E. Wear characteristics of microscopic bushing for MEMS applications investigated by an AFM. J. Micromech. Microeng. 2007, 17, 1877–1887. [Google Scholar] [CrossRef]
- Zhang, L.; Tanaka, H. Atomic scale deformation in silicon monocrystals induced by two-body and three-body contact sliding. Tribol. Int. 1998, 31, 425–433. [Google Scholar] [CrossRef]
- Sun, J.; Fang, L.; Han, J.; Han, Y.; Chen, H.; Sun, K. Abrasive wear of nanoscale single crystal silicon. Wear 2013, 307, 119–126. [Google Scholar] [CrossRef]
- Komanduri, R.; Chandrasekaran, N.; Raff, L.M. Molecular dynamics simulation of the nanometric cutting of silicon. Philos. Mag. B 2001, 81, 1989–2019. [Google Scholar] [CrossRef]
- Tang, Q.; Chen, F. MD simulation of phase transformations due to nanoscale cutting on silicon monocrystals with diamond tip. J. Appl. Phys. 2006, 39, 3674–3679. [Google Scholar] [CrossRef]
- Chrobak, D.; Tymiak, N.; Beaber, A.; Ugurlu, O.; Gerberich, W.W.; Nowak, R. Deconfinement leads to changes in the nanoscale plasticity of silicon. Nat. Nanotechnol. 2011, 6, 480–484. [Google Scholar] [CrossRef]
- Goel, S.; Faisal, N.H.; Luo, X.C.; Yan, J.W.; Agrawal, A. Nanoindentation of polysilicon and single crystal silicon: Molecular dynamics simulation and experimental validation. J. Phys. D Appl. Phys. 2014, 47, 275304. [Google Scholar] [CrossRef]
- Goel, S.; Kovalchenko, A.M.; Stukowski, A.; Cross, G. Influence of microstructure on the cutting behaviour of silicon. Acta Mater. 2016, 105, 464–478. [Google Scholar] [CrossRef] [Green Version]
- Farhat, Z.N.; Ding, Y.; Northwood, D.O.; Alpas, A.T. Effect of grain size on friction and wear of nanocrystalline aluminum. Mater. Sci. Eng. A 1996, 206, 302–313. [Google Scholar] [CrossRef]
- Zhang, Y.S.; Han, Z.; Wang, K.; Lu, K. Friction and wear behaviors of nanocrystalline surface layer of pure copper. Wear 2006, 260, 942–948. [Google Scholar] [CrossRef]
- Ruestes, C.J.; Alhafez, I.A.; Urbassek, H.M. Atomistic Studies of Nanoindentation—A Review of Recent Advances. Crystals 2017, 7, 293. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO-the open visualization tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Schäfer, J.; Stukowski, A.; Albe, K. Plastic deformation of nanocrystalline Pd-Au alloys: On the interplay of grain boundary solute segregation, fault energies and grain size. Acta Mater. 2011, 59, 2957–2968. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity-rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Tersoff, J. Modeling solid-state chemistry-interatomic potentials for multi-component systems. Phys.Rev. B 1989, 39, 5566–5568. [Google Scholar] [CrossRef]
- Fang, F.Z.; Wu, H.; Liu, Y.C. Modeling and Experimental Investigation on Nanometric Cutting of Single-crystalline Silicon. Int. J. Mach. Tools Manuf. 2005, 45, 1681–1686. [Google Scholar] [CrossRef]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Zhao, H.; Shi, C.; Zhang, P.; Zhang, L.; Huang, H.; Yan, J. Research on the effects ofmachining-induced subsurface damages on mono-crystalline silicon via molecular dynamics simulation. Appl. Surf. Sci. 2012, 259, 66–71. [Google Scholar] [CrossRef]
- Zhu, P.Z.; Hu, Y.Z.; Ma, T.B.; Wang, H. Study of AFM-based Nanometric Cutting Process using Molecular Dynamics. Appl. Surf. Sci. 2010, 256, 7160–7165. [Google Scholar] [CrossRef]
- Shi, J.; Shi, Y.; Liu, C.R. Evaluation of Three Dimensional Single Point Turning at Atomistic Level by Molecular Dynamics Simulation. Int. J. Adv. Manuf. Technol. 2010, 8, 161–171. [Google Scholar] [CrossRef]
- Tong, Z.; Liang, Y.; Jiang, X.; Luo, X. An Atomistic Investigation on the Mechanism of Machining Nanostructures when using Single Tip and Multi-Tip Diamond Tools. Appl. Surf. Sci. 2014, 290, 458–465. [Google Scholar] [CrossRef]
- Yan, Y.D.; Sun, T.; Dong, S.; Luo, X.C.; Liang, Y.C. Molecular Dynamics Simulation of Processing using AFM Pin Tool. Appl. Surf. Sci. 2006, 252, 7523–7531. [Google Scholar] [CrossRef]
- Fang, T.; Weng, C. Three-Dimensional Molecular Dynamics Analysis of Processing using a Pin Tool on the Atomic Scale. Nanotechnology 2000, 8, 148–153. [Google Scholar] [CrossRef]
- Zhu, P.Z.; Fang, F.Z. Study of the Minimum Depth of Material Removal in nanoscale Mechanical Machining of single crystalline Copper. Comput. Mater. Sci. 2016, 118, 192–202. [Google Scholar] [CrossRef]
- Ewen, J.P.; Gattinoni, C.; Thakkar, F.M.; Morgan, N.; Spikes, H.A.; Dini, D. Nonequilibrium Molecular Dynamics Investigation of the Reduction in Friction and Wear by Carbon Nanoparticles Between Iron Surfaces. Tribol. Lett. 2016, 63, 38. [Google Scholar] [CrossRef]
- Gao, Y.; Brodyanski, A.; Kopnarski, M.; Urbassek, H.M. Nanoscratching of iron: A molecular dynamics study of the influence of surface orientation and scratching direction. Comput. Mater. Sci. 2015, 103, 77–89. [Google Scholar] [CrossRef]
- Bowden, F.P.; Tabor, D. Friction, lubrication and wear: A survey of work during the last decade. Br. J. Appl. Phys. 1966, 17, 1521–1544. [Google Scholar] [CrossRef]
- Si, L.N.; Guo, D.; Luo, J.B.; Lu, X.C. Monoatomic Layer Removal Mechanism in Chemical Mechanical Polishing Process: A Molecular Dynamics Study. J. Appl. Phys. 2010, 107, 064310. [Google Scholar] [CrossRef]
- Zhu, P.Z.; Hu, Y.Z.; Ma, T.B.; Wang, H. Molecular Dynamics Study on Friction due to Ploughing and Adhesion in Nanometric Scratching Process. Tribol. Lett. 2011, 41, 41–46. [Google Scholar] [CrossRef]
- Li, A.; Szlufarska, I. How grain size controls friction and wear in nanocrystalline metals. Phys. Rev. B 2015, 92, 075418. [Google Scholar] [CrossRef]
- Jeng, Y.-R.; Tsai, P.-C.; Chiang, S.-H. Effects of grain size and orientation on mechanical and tribological characterizations of nanocrystalline nickel films. Wear 2013, 303, 262–268. [Google Scholar] [CrossRef]
- Kopta, S.; Salmeron, M. The atomic scale origin of wear on mica and its contribution to friction. J. Chem. Phys. 2000, 113, 8249–8252. [Google Scholar] [CrossRef]





| Average Grain Size (nm) | Length (nm) | Width (nm) | Height (nm) | Number of Atoms |
|---|---|---|---|---|
| Single crystal | 35.9 | 17.9 | 8.0 | 261,360 |
| 2 | 36.6 | 18.3 | 8.2 | 259,880 |
| 3 | 36.4 | 18.2 | 8.2 | 259,812 |
| 4 | 36.3 | 18.2 | 8.2 | 259,582 |
| 5 | 36.2 | 18.1 | 8.2 | 259,634 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, P.; Li, R.; Gong, H. Molecular Dynamics Simulation of Nanoscale Abrasive Wear of Polycrystalline Silicon. Crystals 2018, 8, 463. https://doi.org/10.3390/cryst8120463
Zhu P, Li R, Gong H. Molecular Dynamics Simulation of Nanoscale Abrasive Wear of Polycrystalline Silicon. Crystals. 2018; 8(12):463. https://doi.org/10.3390/cryst8120463
Chicago/Turabian StyleZhu, Pengzhe, Rui Li, and Hanyu Gong. 2018. "Molecular Dynamics Simulation of Nanoscale Abrasive Wear of Polycrystalline Silicon" Crystals 8, no. 12: 463. https://doi.org/10.3390/cryst8120463
APA StyleZhu, P., Li, R., & Gong, H. (2018). Molecular Dynamics Simulation of Nanoscale Abrasive Wear of Polycrystalline Silicon. Crystals, 8(12), 463. https://doi.org/10.3390/cryst8120463