Intrinsic Ferroelectricity in Charge-Ordered Magnetite
Abstract
:1. Introduction
2. Results and Discussion
2.1. Macroscopic Characterization
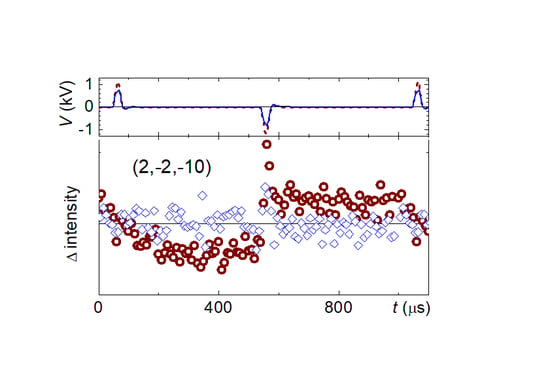
2.2. Time-Resolved X-ray Diffraction with Voltage Pulses Applied In-Situ
3. Summary
4. Materials and Methods
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CO | charge order |
| DFT | density functional theory |
| EXAFS | extended x-ray absorption fine structure |
| PUND | positive-up-negative-down |
| VRH | variable-range hopping |
| HV | high-voltage |
| FPGA | field-programmed gate array |
| PPMS | physical properties measurement system |
| HF | high frequency |
References
- Verwey, E.J.W. Electronic Conduction of Magnetite (Fe3O4) and its Transition Point at Low Temperatures. Nature 1939, 144, 327. [Google Scholar] [CrossRef]
- Garcia, J.; Subias, G. The Verwey transition—A new perspective. J. Phys. Condens. Matter 2004, 16, R145. [Google Scholar] [CrossRef]
- Senn, M.S.; Wright, J.P.; Attfield, J.P. Charge order and three-site distortions in the Verwey structure of magnetite. Nature 2012, 481, 173. [Google Scholar] [CrossRef] [PubMed]
- Yamauchi, K.; Tetsuya, T.; Piccozzi, S. Ferroelectricity in multiferroic magnetite Fe3O4 driven by noncentrosymmetric Fe2+/Fe3+ charge-ordering: First-principles study. Phys. Rev. B 2009, 79, 212404. [Google Scholar] [CrossRef]
- Van den Brink, J.; Khomskii, D.I. Multiferroicity due to charge ordering. J. Phys.: Condens. Matter 2008, 20, 434217. [Google Scholar] [CrossRef]
- Angst, M. Charge Order-Driven Multiferroicity. In Multiferroic Materials—Properties, Techniques, and Applications; Wang, J., Ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2016; Chapter 3; pp. 67–97. [Google Scholar]
- Ikeda, N.; Ohsumi, H.; Ohwada, K.; Ishii, K.; Inami, T.; Kakurai, K.; Murakami, Y.; Yoshii, K.; Mori, S.; Horibe, Y.; et al. Ferroelectricity from Iron Valence Ordering in the Charge-Frustrated System LuFe2O4. Nature 2005, 436, 1136. [Google Scholar] [CrossRef]
- De Groot, J.; Mueller, T.; Rosenberg, R.A.; Keavney, D.J.; Islam, Z.; Kim, J.W.; Angst, M. Charge Order in LuFe2O4: An Unlikely Route to Ferroelectricity. Phys. Rev. Lett. 2012, 108, 187601. [Google Scholar] [CrossRef]
- Niermann, D.; Waschkowski, F.; de Groot, J.; Angst, M.; Hemberger, J. Dielectric Properties of Charge-Ordered LuFe2O4 Revisited: The Apparent Influence of Contacts. Phys. Rev. Lett. 2012, 109, 016405. [Google Scholar] [CrossRef]
- Angst, M. Ferroelectricity from iron valence ordering in rare earth ferrites? Phys. Status Solidi RRL—Rapid Res. Lett. 2013, 7, 383–400. [Google Scholar] [CrossRef] [Green Version]
- Rado, G.T.; Ferrari, J.M. Electric Field Dependence of the Magnetic Anisotropy Energy in Magnetite (Fe3O4). Phys. Rev. B 1975, 12, 5166. [Google Scholar] [CrossRef]
- Kato, K.; Iida, S. Observation of Ferroelectric Hysteresis Loop of Fe3O4 at 4.2 K. J. Phys. Soc. Jpn. 1982, 51, 1335–1336. [Google Scholar] [CrossRef]
- Kato, K.; Iida, S.; Yanai, K.; Mizushima, K. Ferrimagnetic ferroelectricity of Fe3O4. J. Magn. Magn. Mater. 1983, 31–34, 783. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Chikazumi, S. Crystal Symmetry of Magnetite in Low Temperature Phase Deduced from Magnetoelectric Measurements. J. Phys. Soc. Jpn. 1988, 57, 2040. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Kameda, T.; Ishihara, S.; Chikazumi, S. Magnetoelectric polarization for twinned crystal of magnetite below 125 K. Ferroelectrics 1989, 93, 301–308. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Shindo, M. Magnetoelectric Measurement of Magnetite (Fe3O4) at Low Temperatures and Direct Evidence for Nonexistence of ac Mirror Plane. J. Phys. Soc. Jpn. 1993, 62, 1423. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Ishihara, S.; Hirano, T.; Takada, M.; Suzuki, N. Ferroelectricity of magnetite (Fe3O4) observed by means of magnetoelectric effect. Solid State Commun. 1994, 89, 51–54. [Google Scholar] [CrossRef]
- Alexe, M.; Ziese, M.; Hesse, D.; Esquinazi, P.; Yamauchi, K.; Fukushima, T.; Picozzi, S.; Gösele, U. Ferroelectric Switching in Multiferroic Magnetite (Fe3O4) Thin Films. Adv. Mater. 2009, 21, 4452–4455. [Google Scholar] [CrossRef]
- Scott, J.F.; Kammerdiner, L.; Parris, M.; Traynor, S.; Ottenbacher, V.; Shawabkeh, A.; Oliver, W.F. Switching kinetics of lead zirconate titanate submicron thin-film memories. J. Appl. Phys. 1988, 64, 787–792. [Google Scholar] [CrossRef]
- Fina, I.; Fàbrega, L.; Martí, X.; Sánchez, F.; Fontcuberta, J. Chiral Domains in Cycloidal Multiferroic Thin Films: Switching and Memory Effects. Phys. Rev. Lett. 2011, 107. [Google Scholar] [CrossRef]
- Schrettle, F.; Krohns, S.; Lunkenheimer, P.; Brabers, V.A.M.; Loidl, A. Relaxor ferroelectricity and the freezing of short-range polar order in magnetite. Phys. Rev. B 2011, 83, 195109. [Google Scholar] [CrossRef] [Green Version]
- Bokov, A.A.; Ye, Z.G. Dielectric dispersion and critical behavior in relaxor ferroelectric Pb(Mg1/3Nb2/3)O3-PbTiO3. Appl. Phys. Lett. 2000, 77, 1888. [Google Scholar] [CrossRef]
- Cross, L.E. Relaxor ferroelectrics. Ferroelectrics 1987, 76, 241–267. [Google Scholar] [CrossRef]
- Shepherd, J.P.; Koenitzer, J.W.; Aragon, R.; Spallek, J.; Honig, J.M. Heat Capacity and Entropy of Nonstoichiometric Magnetite Fe3(1−δ)O4: The Thermodynamic Nature of the Verwey Transition. Phys. Rev. B 1991, 43, 8461. [Google Scholar] [CrossRef] [PubMed]
- Aragón, R.; Gehring, P.M.; Shapiro, S.M. Stoichiometry, percolation, and Verwey ordering in magnetite. Phys. Rev. Lett. 1993, 70, 1635–1638. [Google Scholar] [CrossRef]
- Maxwell, J.C. Treatise on Electricity and Magnetism, 3rd ed.; Dover: New York, NY, USA, 1991. [Google Scholar]
- Wagner, K.W. Zur Theorie der unvollkommenen Dielektrika. Annalen der Physik 1913, 345, 817. [Google Scholar] [CrossRef]
- Lunkenheimer, P.; Bobnar, V.; Pronin, A.V.; Ritus, A.I.; Volkov, A.A.; Loidl, A. Origin of apparent colossal dielectric constants. Phys. Rev. B 2002, 66. [Google Scholar] [CrossRef]
- Loidl, A.; Krohns, S.; Hemberger, J.; Lunkenheimer, P. Bananas Go Paraelectric. J. Phys.: Condens. Mat. 2008, 20, 191001. [Google Scholar] [CrossRef]
- Ruff, A.; Krohns, S.; Schrettle, F.; Tsurkan, V.; Lunkenheimer, P.; Loidl, A. Absence of polar order in LuFe2O4. Eur. Phys. J. B 2012, 85, 290. [Google Scholar] [CrossRef]
- Jonscher, A.K. Universal Relaxation Law; Chelsea Dielectrics Press: New York, NY, USA, 1996. [Google Scholar]
- Elliott, S.R. Ac conduction in amorphous chalcogenide and pnictide semiconductors. Adv. Phys. 1987, 36, 135. [Google Scholar]
- Shklovskii, B.I.; Efros, A.L. Electronic Properties of Doped Semiconductors; Springer: Berlin, Germany, 1984. [Google Scholar]
- Merz, W.J. Domain Formation and Domain Wall Motions in Ferroelectric BaTiO3 Single Crystals. Phys. Rev. 1954, 95, 690–698. [Google Scholar] [CrossRef]
- Niermann, D.; Grams, C.; Schalenbach, M.; Becker, P.; Bohatý, L.; Stein, J.; Braden, M.; Hemberger, J. Domain dynamics in the multiferroic phase of MnWO4. Phys. Rev. B 2014, 89, 134412. [Google Scholar] [CrossRef]
- Grams, C.; Kopatz, S.; Brüning, D.; Biesenkamp, S.; Becker, P.; Bohatý, L.; Lorenz, T.; Hemberger, J. Evidence for polarized nanoregions from the domain dynamics in multiferroic LiCuVO4. Sci. Rep. 2019, 9, 4391. [Google Scholar] [CrossRef] [PubMed]
- Friedel, G. Sur les symétries cristallines que peut révéler la diffraction des rayons X. C. R. Acad. Sci. 1913, 157, 1533. [Google Scholar]
- Thiessen, P.A.; Molière, K. Über den Einfluß der Absorption auf den Brechungseffekt der Elektronenstrahlen. I. Teil. Messungen des inneren Potentials an den polaren Tetraederflächen der Zinkblende. Annalen der Physik 1939, 34, 449. [Google Scholar] [CrossRef]
- Azimonte, C.; Granado, E.; Terashita, H.; Park, S.; Cheong, S.W. Polar atomic displacements in multiferroics observed via anomalous X-ray diffraction. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
- Gorfman, S.; Simons, H.; Iamsasri, T.; Prasertpalichat, S.; Cann, D.P.; Choe, H.; Pietsch, U.; Watier, Y.; Jones, J.L. Simultaneous resonant X-ray diffraction measurement of polarization inversion and lattice strain in polycrystalline ferroelectrics. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef]
- Strempfer, J.; Francoual, S.; Reuther, D.; Shukla, D.K.; Skaugen, A.; Schulte-Schrepping, H.; Kracht, T.; Franz, H. Resonant scattering and diffraction beamline P09 at PETRA III. J. Synchrotron Rad. 2013, 20, 541–549. [Google Scholar] [CrossRef]
- Gorfman, S.; Schmidt, O.; Ziolkowski, M.; von Kozierowski, M.; Pietsch, U. Time-resolved X-ray diffraction study of the piezoelectric crystal response to a fast change of an applied electric field. J. Appl. Phys. 2010, 108, 064911. [Google Scholar] [CrossRef]
- Gorfman, S. Sub-microsecond X-ray crystallography: Techniques, challenges, and applications for materials science. Crystallogr. Rev. 2014, 20, 210–232. [Google Scholar] [CrossRef]
- Gorfman, S.; Choe, H.; Shvartsman, V.V.; Ziolkowski, M.; Vogt, M.; Strempfer, J.; Łukasiewicz, T.; Pietsch, U.; Dec, J. Time-Resolved X-Ray Diffraction Reveals the Hidden Mechanism of High Piezoelectric Activity in a Uniaxial Ferroelectric. Phys. Rev. Lett. 2015, 114. [Google Scholar] [CrossRef] [Green Version]
- Zhang, N.; Gorfman, S.; Choe, H.; Vergentev, T.; Dyadkin, V.; Yokota, H.; Chernyshov, D.; Wang, B.; Glazer, A.M.; Ren, W.; et al. Probing the intrinsic and extrinsic origins of piezoelectricity in lead zirconate titanate single crystals. J. Appl. Crystallogr. 2018, 51, 1396–1403. [Google Scholar] [CrossRef]
- Petricek, V.; Dusek, M.; Palatinus, L. Crystallographic Computing System JANA2006: General features. Z. Kristallogr. 2014, 229, 345–352. [Google Scholar]
- Mueller, T.; de Groot, J.; Strempfer, J.; Angst, M. Stoichiometric YFe2O4−δ single crystals grown by the optical floating zone method. J. Cryst. Growth 2015, 428, 40. [Google Scholar] [CrossRef]
- Hammouda, S.; Angst, M. Growth of layered Lu2Fe3O7 and Lu3Fe4O10 single crystals exhibiting long-range charge order via the optical floating-zone method. J. Cryst. Growth 2019, 521, 50–54. [Google Scholar] [CrossRef]
- de Groot, J.; Marty, K.; Lumsden, M.D.; Christianson, A.D.; Nagler, S.E.; Adiga, S.; Borghols, W.J.H.; Schmalzl, K.; Yamani, Z.; Bland, S.R.; et al. Competing Ferri- and Antiferromagnetic Phases in Geometrically Frustrated LuFe2O4. Phys. Rev. Lett. 2012, 108, 037206. [Google Scholar] [CrossRef]
- Mo/lgaard, J.; Smeltzer, W.W. Thermal Conductivity of Magnetite and Hematite. J. Appl. Phys. 1971, 42, 3644–3647. [Google Scholar] [CrossRef]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angst, M.; Adiga, S.; Gorfman, S.; Ziolkowski, M.; Strempfer, J.; Grams, C.; Pietsch, M.; Hemberger, J. Intrinsic Ferroelectricity in Charge-Ordered Magnetite. Crystals 2019, 9, 546. https://doi.org/10.3390/cryst9110546
Angst M, Adiga S, Gorfman S, Ziolkowski M, Strempfer J, Grams C, Pietsch M, Hemberger J. Intrinsic Ferroelectricity in Charge-Ordered Magnetite. Crystals. 2019; 9(11):546. https://doi.org/10.3390/cryst9110546
Chicago/Turabian StyleAngst, Manuel, Shilpa Adiga, Semen Gorfman, Michael Ziolkowski, Jörg Strempfer, Christoph Grams, Manuel Pietsch, and Joachim Hemberger. 2019. "Intrinsic Ferroelectricity in Charge-Ordered Magnetite" Crystals 9, no. 11: 546. https://doi.org/10.3390/cryst9110546
APA StyleAngst, M., Adiga, S., Gorfman, S., Ziolkowski, M., Strempfer, J., Grams, C., Pietsch, M., & Hemberger, J. (2019). Intrinsic Ferroelectricity in Charge-Ordered Magnetite. Crystals, 9(11), 546. https://doi.org/10.3390/cryst9110546