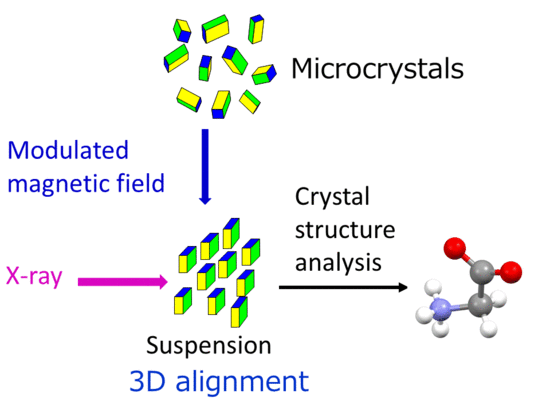
X-ray Single-Crystal Structural Analysis of a Magnetically Oriented Monoclinic Microcrystal Suspension of α-Glycine

Abstract

We previously reported on a method for X-ray single-crystal structure determination from a powder sample via a magnetically oriented microcrystal suspension (MOMS). The method was successfully applied to orthorhombic microcrystals (L-alanine, P2₁2₁2₁). In this study, we apply this method to monoclinic microcrystals. Unlike most of the orthorhombic MOMSs, monoclinic MOMSs exhibit two or four orientations with the same magnetic energy (we refer to this as twin orientations), making data processing difficult. In this paper, we perform a MOMS experiment for a powder sample of monoclinic microcrystal (α-glycine, P2₁/n) to show that our method can also be applied to monoclinic crystals. The single-crystal structure determined in this work is in good agreement with the reported one performed on a real single crystal. Furthermore, the relationship between the crystallographic and magnetic susceptibility axes is determined.

1. Introduction

Single-crystal structure determination is a key issue in materials and pharmaceutical sciences, because the physical, chemical, and biological functions are closely related to the molecular and crystal structures. The X-ray diffraction method is most suited to crystal structure determination if a single crystal that is large enough for the measurement is available. However, in many circumstances, samples are obtained only in the form of microcrystalline powders, which hinders the use of the single-crystal method [1]. In such circumstances, the powder method is applied, which does not need a large single crystal [2]. However, this method is not suitable in general for analyzing complicated organic compounds and large molecules, such as proteins, although there are reports on the crystal structure determination of proteins using the powder method [3,4].

We proposed a method that combines the magnetic orientation of microcrystals and X-ray single-crystal analysis. In this method, a microcrystal suspension is biaxially aligned using a magnetic field to obtain a “magnetically oriented microcrystal suspension” (MOMS) [5,6]. Then, the MOMS is subjected to in situ single-crystal X-ray analysis [7,8,9], or its suspending medium is consolidated to obtain a “magnetically oriented microcrystal array” (MOMA) to perform the single-crystal X-ray analysis ex situ [10,11]. The biaxial alignment was first reported by Stainer to align superconducting materials [12,13].

If the intensity of the magnetic field used is the same, the resolution achieved by MOMA is lower than that of MOMS, because in MOMA, the achieved orientation of the suspension partially deteriorates during the consolidation process of the suspending medium. On the other hand, magnets available for MOMS are limited to permanent magnets because of the limitation of the space required for the in situ X-ray measurement. Permanent magnets can only supply magnetic fields up to 1 T. On the other hand, much higher magnetic fields, such as those supplied by superconducting magnets (~ 10 T) can be used to prepare MOMAs, resulting in higher orientations. Usually, MOMAs prepared with higher magnetic fields can exhibit equal or higher orientation than MOMSs.

So far, we have performed single-crystal structure determination of inorganic [14], organic [10], and protein microcrystals [11] by using MOMA. Those crystals belong to the orthorhombic [11,14] and monoclinic [10] systems. We also performed single-crystal structure determination of orthorhombic crystals using MOMS [7,8,9]. Magnetically aligned monoclinic microcrystals exhibit twin orientations [10], which makes the analysis of MOMA complicated (sucrose [10], cellobiose [15], and zinc citrate dihydrate [16]). A further complication arises because the MOMS method is performed in situ. In this study, in situ X-ray measurement was performed on the MOMS of monoclinic microcrystals of α-glycine, and the crystal structure was determined. In addition, the relationship between the crystallographic and magnetic axes was determined.

2. Experimental Methods

The as-received glycine (Wako Pure Chemical Industries, Ltd., Tokyo, Japan) was in the γ-form (hexagonal). Recrystallization was performed to obtain monoclinic α-glycine as follows [17]: The as-received sample was dissolved in ca. 100 μmol/L MgCl₂·6H₂O solution until saturation and kept in a refrigerator until crystallization of the α-form. The α-glycine crystals obtained were pulverized with a mortar and pestle and passed through 125-, 75-, 45-, and 20-mesh sieves, consecutively. Then, the powder remaining on the 20-mesh sieve was dispersed in a UV light-curable monomer (XVL-14, viscosity 12 ± 2 Pa s, Kyoritsu Chemical & Co., Ltd., Tokyo, Japan) to obtain a 20 wt % α-glycine microcrystalline suspension. The UV light-curable monomer was used only for the purpose of obtaining a stable and well-dispersed microcrystal suspension. In order to remove the large and aggregated microcrystals, the suspension was allowed to stand overnight at 40 °C. The middle layer of the suspension was taken with a pipette and poured into a glass capillary with a diameter of 1.5 mm.

The capillary was rotated in a frequency-modulated rotation manner in a magnetic field produced by a pair of neodymium magnets (~1 T in the center). The rotation speeds were switched every 90° between ${\omega }_{\mathrm{s}}=$1 and ${\omega }_{\mathrm{f}}=$3 rpm. The rotation/magnetic unit was mounted on a Rigaku R-Axis Rapid II diffractometer equipped with a rotating beam shutter that rotated synchronously with the rotation of the capillary. The slit angle of the shutter was 10°. The frequency-modulated rotation was maintained during the X-ray measurement. The details of the measurement have been reported elsewhere [7].

The capillary was first set perpendicular to the X-ray incidence direction (defined as $\alpha =$90° in Figure 1a), and the X-ray diffraction measurements were performed from $\varphi =-45$ up to 145° (Figure 1b), with a sample oscillation angle of 10° (slit angle). Furthermore, the capillary was tilted by an angle of $\alpha =$120° in the horizontal plane, and the oscillation measurements were performed in the same manner as for $\alpha =$90°. The exposure time was 15 s/°. The X-ray source was MoKα, and the camera length was 147 mm.

The crystal structure analysis was performed as follows: Indexing of twin orientations was performed on the obtained diffraction images using processing software RAPID AUTO Ver. 4.3 provided by Rigaku Corporation. The integration and scaling were performed to obtain reflection profiles from each of the twin components. One component was used to determine the space group, followed by determination of the initial structure by a direct method (SHELXT-2014) [18] using CrystalStructure 4.3 software [19]. Then, refinement was performed using SHELX-2017 [20].

3. Results and Discussion

The magnetic susceptibility tensor of the biaxial crystal in orthorhombic, monoclinic, and triclinic systems has three different principal values, ${\chi }_1$, ${\chi }_2$, and ${\chi }_3,$ and the corresponding principal axes. For the orthorhombic system, the crystallographic and magnetic axes coincide. For the monoclinic system, the b axis coincides with one of the magnetic axes. For the triclinic system, there is no general relationship between the crystallographic and magnetic axes. Owing to their biaxial magnetic nature, biaxial crystals can be aligned biaxially (or three-dimensionally) if an appropriate dynamic magnetic field (DMF) is applied [21,22,23,24,25]. Among the biaxial crystals, most orthorhombic crystals exhibit only one orientation under DMF, because the crystallographic and magnetic susceptibility axes coincide. On the other hand, the monoclinic and triclinic crystals exhibit two or four orientations (twin orientations) that have the same magnetic energy [26].

Figure 2 shows a polarized microphotograph of the suspension of the α-glycine microcrystals. The size distribution of the microcrystals was approximately 1–40 μm, and each of the microcrystals shows almost uniform color, indicating that they are single crystals. Figure 3a–c shows X-ray diffraction images recorded at three different oscillation angles: (a) ϕ = 5 to 15° at α = 90°, (b) ϕ = 95 to 105° at α = 90°, and (c) ϕ = 35 to 45° at α = 120°. These images clearly exhibit different profiles, indicating that the suspension is aligned biaxially.

The XRD images were indexed, and two components were detected. The crystal system, the space group, and the lattice parameters of α-glycine determined from the MOMS were monoclinic, P2₁/n, and a = 5.0833(10), b = 11.902(3), c = 5.4399(9) Å, and β = 111.67(2)°, respectively. The R₁ and wR₂ values were 0.0595 and 0.1663. The crystallographic data [27] and the determined structure from the MOMS were in good agreement with those determined from the single crystal (

Table 1. Crystallographic data obtained from a three-dimensional (3D) MOMS and single crystal of α-glycine.

Sample	α-Glycine MOMS	α-Glycine SC [25]
Crystal system	Monoclinic	monoclinic
Space group	P21/n	P21/n
Temperature (K)	296	288
a (Å)	5.0833(10)	5.0993(3)
b (Å)	11.902(3)	11.9416(6)
c (Å)	5.4399(9)	5.4608(3)
V (Å3)	305.87(12)	308.78(3)
Z	4	4
β (°)	111.67(2)	111.784(2)
2θmax	50.0 (Mo Kα)	90.0 (neutrons)
Reflection	412	1540
Completeness	0.770
Rint	0.0939	-
R1 [F2> 2σ(F2)]	0.0595	0.0371
wR2 [all data]	0.1675	0.0777
GOF	1.241	1.204
CCDC No.	1957082	849662 Glycin96

and Figure 4; root-mean-square deviation of 0.0133 Å). In the present experimental setting, the oscillation was set only about the sample rotating axis, resulting in less completeness. In addition, the overlapped diffraction peaks due to the twin orientation were removed from the data set. This caused the decrease in a number of available diffraction peaks.

Figure 5 shows the XRD image of the MOMS of α-glycine taken at α = 90° with an oscillation angle ϕ of 35° to 45°. All the images taken at α = 90° showed evenly separated vertical layered lines. These lines show a sort of fiber diffraction pattern, because the aligned suspension is rotated about a horizontal rotation axis. Each space between the nearest layers is ca. 11.5 Å, which is close to b (= 11.9 Å), indicating that the diffraction spots in lines are due to (hkl), Miller index, with k = 0, ±1, ±2, … and with the b axis being horizontal. On the other hand, it is known that the axis of sample rotation coincides with the ${\chi }_3$ magnetic axis. Therefore, the b axis is assigned to the ${\chi }_3$ axis, which is consistent with the fact that the b axis is a two-fold axis.

The diffraction data indicate that there are two orientational twins, twin 1 and twin 2. The software analysis showed that the angles $\widehat{a_1{a}_2}$, $\widehat{b_1{b}_2}$, and $\widehat{ c_1{c}_2}$, were 46.32°, 179.21°, and 89.65°, respectively, where the suffices 1 and 2 represent twin 1 and twin 2. The value of $\widehat{b_1{b}_2}$= 179.21° ($\cong 180°$) suggested that the b axis was shared by the twins (the $b_1$ axis was antiparallel to the $b_2$ axis). Under this condition, two twin orientations were located, as shown in Figure 6. Furthermore, ${\chi }_1$ and ${\chi }_2$ were determined with respect to the crystallographic axes. The angle between the c axis and the ${\chi }_1$ axis was determined to be 45.18°.

In the molecule of α-glycine, O=C–O forms a plane, which might provide a major part of magnetic anisotropy. The ${\chi }_3$ axis might be directly perpendicular to the plane. Figure 7 shows molecules in the unit cell viewed from the c* axis. We found that the O=C–O planes were almost perpendicular to the b axis. This is consistent with the fact that ${\chi }_3\left|\right|b$.

4. Conclusions

A suspension of monoclinic microcrystalline powder of α-glycine was magnetically aligned and subjected to in situ X-ray diffraction measurement. The obtained diffraction data were analyzed using twin-indexing software to solve the crystal structure. The result obtained was in good agreement with the structure reported, demonstrating that the MOMS can be applicable to monoclinic crystals (possibly triclinic crystals), which exhibit twin structures when magnetically aligned. The method is also useful for the determination of the magnetic axis of monoclinic crystals with respect to the crystallographic axes.