Next Article in Journal
Van der Waals Density Functional Theory vdW-DFq for Semihard Materials
Next Article in Special Issue
Dihydrogen Bonds in Salts of Boron Cluster Anions [BnHn]2− with Protonated Heterocyclic Organic Bases
Previous Article in Journal
Dielectric Relaxor and Conductivity Mechanism in Fe-Substituted PMN-32PT Ferroelectric Crystal
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 9
Issue 5
10.3390/cryst9050242
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

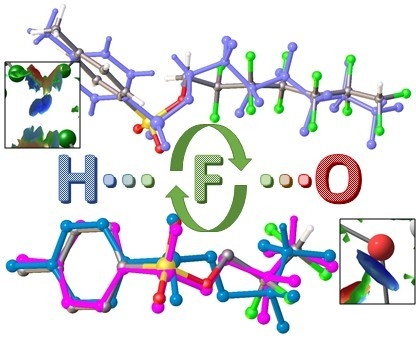
Molecular Structures Polymorphism the Role of F…F Interactions in Crystal Packing of Fluorinated Tosylates

by
Dmitry E. Arkhipov
1,
Alexander V. Lyubeshkin
2,
Alexander D. Volodin
1 and
Alexander A. Korlyukov
1,*
1
A.N.Nesmeyanov Institute of Organoelement Compounds of Russian Academy of Sciences, 119991 Moscow, Russia
2
Federal Scientific Research Center “Crystallography and Photonics” of Russian Academy of Sciences, 119333 Moscow, Russia
*
Author to whom correspondence should be addressed.
Crystals 2019, 9(5), 242; https://doi.org/10.3390/cryst9050242
Submission received: 19 April 2019 / Revised: 4 May 2019 / Accepted: 5 May 2019 / Published: 7 May 2019
(This article belongs to the Special Issue Chemical Bonding in Crystals and Their Properties)
Browse Figures
Versions Notes

Abstract

:
The peculiarities of interatomic interactions formed by fluorine atoms were studied in four tosylate derivatives p-CH3C6H4OSO2CH2CF2CF3 and p-CH3C6H4OSO2CH2(CF2)nCHF2 (n = 1, 5, 7) using X-ray diffraction and quantum chemical calculations. Compounds p-CH3C6H4OSO2CH2(CF2)nCHF2 (n = 1, 5) were crystallized in several polymorph modifications. Analysis of intermolecular bonding was carried out using QTAIM approach and energy partitioning. All compounds are characterized by crystal packing of similar type and the contribution of intermolecular interactions formed by fluorine atoms to lattice energy is raised along with the increase of their amount. The energy of intra- and intermolecular F…F interactions is varied in range 0.5–13.0 kJ/mol. Total contribution of F…F interactions to lattice energy does not exceed 40%. Crystal structures of studied compounds are stabilized mainly by C-H…O and C-H…F weak hydrogen bonds. The analysis of intermolecular interactions and lattice energies in polymorphs of p-CH3C6H4OSO2CH2(CF2)nCHF2 (n = 1, 5) has shown that most stabilized are characterized by the least contribution of F…F interactions.

Graphical Abstract

1. Introduction

Organosulfur compounds containing fluorinated hydrocarbon moieties are usually considered as dangerous hydrocarbon pollutants that destroy cell membranes [1,2]. Among these compounds, perfluoroalkyl sulfonates, perfluoroalkyl sulfoacids, and sulfamides are the most dangerous and pervasive in environment owing to their high stability and surfactant properties. On the other hand, there are examples of application of above compounds in medicine as drug delivery vehicles [3,4] and antimicrobial agents [5]. The presence of perfluorinated hydrocarbon moiety plays special role in binding of these compounds with biomolecules in solution and in complexes with proteins via hydrophobic interactions. For instance, perfluorooctane sulfuric acid can occupy the position between peptide chains of serum albumin [6] mostly via weak van-der-Waals H…F interactions. Besides, perfluoroalkyl chains can form aggregates (molecular ensembles, micelles [7], liquid crystal phases [8]) in which the role of F…F interactions can be considerable. The crystal structure can be considered as a model for molecular associations of such compounds; and XRD techniques allow studying the nature of weak intermolecular interactions in detail. The nature of interactions formed by fluorine atoms in organic crystals was extensively studied in many articles [9,10,11,12,13,14,15]. Typically, intermolecular interactions in solids containing CF3 groups or fluorinated aromatic fragments are studied. Only few papers devoted to investigation of compounds with alkyl perfluorinated substituents were published to date [16,17]. Unfortunately, the computational studies in these articles are limited to dimers extracted from crystal packing. In present paper we studied the nature of molecular association in four tosylate derivatives with CF3 (1) and (CF2)nCHF2 (n = 1, 5, 7 in 2–4) groups using single crystal X-ray diffraction and quantum chemical calculations utilizing periodic boundary conditions. Compounds 2 and 3 were crystallized in two polymorphic modifications (2a, 2b, 3a, and 3b).
The studied compounds were synthesized as precursors for preparation of fluorinated azides. In turn, they can be used for modification of biologically active molecules such as various antibacterial agents. The compounds described herein contain fluorinated hydrocarbon moiety of different size from short (C2F5 and CF2CHF2) to long (CF2)7CHF2), thus giving the opportunity to discover and compare the effect of substituent on crystal packing and physicochemical properties of 1–4.

2. Materials and Methods

2.1. Chemicals and Reagents

All chemicals in this article were received from Sigma-Aldrich Chemical Company (St. Louis, MI, USA) with pure grade.

2.2. Synthesis of Tosylates 1–4

General synthetic route for 1–4 was published by Yoshida [18] and used as is. Tosyl chloride (2.1 g, 11 mmol) in dichloromethane (20 mL) was added to a stirred suspension of an fluorinated alcohol HOCH2CF2CF3 and HOCH2(CF2)nCHF2 (n = 1, 5, 7) (10 mmol), KOH (0.84 g, 15 mmol), triethylamine (10 mg, 0.1 mmol) and trimethylamine hydrochloride (0.1 g, 1 mmol) in dichloromethane (20 mL) at 5–10 °C, and the mixture was stirred for 1 h and at room temperature for 3–5 h. 20 mL aqueous 1 M hydrochloric acid solution was added to the mixture, the organic layer was separated, washed once with 20 ml of water and dried with anhydrous sodium sulfate. The precipitate was filtered off; the solvent was evaporated on a rotor, obtaining the desired tosylates. The melting points were identical to published data: 1 (52–53 [19]), 2 (13–15 [20]), 3 (34–35 [21]), and 4 (43–44 °C [20]). The yields for 1–4 are equal to 80, 87, 95, and 95%, respectively. The crystals suitable for X-ray analysis were obtained from reaction mass (1, 2a, and 4) and grown from liquid samples (2b, 3a, and 3b).

2.3. Single Crystal Structure Analysis

Single crystal X-ray studies of 1–4 were carried out in Center for molecule composition studies of INEOS RAS using Bruker APEX II and Bruker APEX DUO diffractometers. All crystal samples were colorless crystals with low melting point. To prevent damage of the samples and decrease of thermal movement of atoms the measurements were carried out at 120 K.
The structures were solved by direct method and refined in anisotropic approximation for non-hydrogen atoms. Hydrogens atoms of methyl, methylene and aromatic fragments were calculated according to those idealized geometry and refined with constraints applied to C-H bond lengths and equivalent displacement parameters (Uiso(H) = 1.2Ueq(C) for CH2, and CH; Uiso(H) = 1.5Ueq(C) for CH3 group. All structures were solved with the ShelXT [22] program and refined with the ShelXL [23] program. Molecular graphics was drawn using OLEX2 [24] program. The structure 3a was refined as inversion twin using TWIN and BASF instructions (Flack parameter is equal to 0.11(17)). CCDC 1907454-1907459 and Table S1 contain the supplementary crystallographic data for 1–4. These data can be obtained free of charge from The Cambridge Crystallographic Data Centre via https://www.ccdc.cam.ac.uk/structures.

2.4. Quantum Chemical Calculations

All DFT calculations were performed within the PBE exchange-correlation functional using VASP 5.4.1 [25,26,27,28]. Atomic coordinates were optimized; however, cell parameters were fixed at their experimental values to prevent cell contraction or expansion (total energies are summarized in Table S2, optimized coordinates can be found in of electronic supplementary information (VASP calculation output section)). To improve the description of van-der-Waals interactions D3 correction [29] was applied. Atomic cores were described using PAW potentials. Valence electrons (2s and 2p for O and N atoms; 3p, and 3s for S; 1s for H) were described in terms of a plane-wave basis set (the kinetic energy cutoff was at 800 eV). VASP is supplied with library of small-core PAW potentials. Thus, the problems with topological analysis due to usage of pseudopotentials was avoided for intermolecular interactions. The electron density function suitable for analysis in terms of QTAIM theory was obtained in separate single-point calculations of the optimized structures of 1–4 using the fast Fourier transform grid that was twice as dense as the default values (the distances between points in direct space were ~0.03 Å). Topological analysis of electron density in terms QTAIM was carried out with AIM program (a part of ABINIT code [30]). NCI analysis was performed using CRITIC2 software [31].
The energies of intermolecular interactions were evaluated using Espinosa, Mollins and Lecomte correlation formula [32]. The sum of energies of all intermolecular interaction can be associated with the values of lattice energy. In addition to topological analysis, lattice energies were obtained using energy decomposition procedure implemented into CrystalExplorer17 program [33]. The latter approach used experimental X-ray coordinates, while all bonds with hydrogen atoms were normalized to value from neutron diffraction studies. In contrast to VASP calculations, Crystal Explorer used localized basis set 6–31G(d,p) and B3LYP functional. Calculated energies were scaled to account counterpoise and dispersion corrections.

3. Results and Discussion

3.1. Geometry and Crystal Packing of 1–4

General views of molecules 1–4 are presented at Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, while the information about the most important structural parameters is summarized in Table 1 (in addition, molecular structures of 2b and 3b are shown at Figures S1 and S2 in supplementary). All compounds crystallized in monoclinic cell. Asymmetric unit of 2b contains two molecules denoted as A and B. Other structures are characterized by Z = 1. Bond lengths in tosylate and fluoroalkyl moieties are the same as in the case of similar sulfonates and fluorinated alcohol derivatives in CSD [34]. The length of the terminal C–F and C-C bonds is a bit shorter than in the case of difluoromethylene moieties vicinal to sulfonate ones.
Mutual orientation of a flurorinated alkyl and a tosyl moiety is governed by crystal packing. Torsion angles C1-S1-O1-C8 in 1 and 4 are equal to 71.51(13) and 68.42(13)°, respectively. Conformation of the hydrocarbon chain in polymorph 2a is almost the same as in molecule A of polymorph 2b (angle C1-S1-O1-C8 is equal to −69.23(12) and −74.894(6)°) while molecule B has another conformation (the angles C1-S1-O1-C8 is equal to 77.208(7)°). In polymorphs 3a and 3b this angle is equal to −85.8(4) and −69.8(2)°, correspondingly.
Compounds 1–4 form similar crystal packing, which can be described as a tail-to-tail arrangement of molecules (Figure 7, Figure 8 and Figure 9). It is noteworthy that the values of b side in 1–4 are always equal. Besides, the fluoroalkyl fragments are assembled together, however, there are differences in mutual disposition of molecules in crystal packing. Analysis of short contacts between atoms of these fragments in 1 (Figure 7a) revealed the absence of F…F contacts (all F…F distances exceed the sum of those van-der-Waals radii that is equal to 2.9 Å [35]). The most pronounced intermolecular interactions are weak C–H…O hydrogen bonds and C–H…π interactions between tosylate moieties. In the case of bulky fluoroalkyl fragments (2–4), the F…F distances became shorter. In several cases these distances are considerably shorter than 2.9 Å (for instance, F3…F8[1 − x, −1/2 + Y, 1 − Z] and F7…F5[x, −1 + y, z] distances in 3a and 4 are equal to 2.764(4) and 2.5112(17) Å, respectively). Additional characterization of F…F contacts using pair C–F…F–C angles has shown that first angle is close to linear (142–170°), while the second one varies in wide range (106–161°). Generally, the shorter F…F distance the closer both angles are to 180° that corresponds to halogen-halogen contact of type I according to classification by Desiraju [36]. According to CSD [34], this picture is typical for compounds with polyfluoroalkyl fragments.
Despite the amount of fluorine atoms only few H…F contacts were found in 1–4. The strongest contacts are related to the formation of C–H…F bond with terminal difluoromethyl group. The latter bond can be described as an additional factor that is assisted for arrangement of fluoroalkyl moieties. Thus, the contribution of F…F to energy of crystalline packing noticeably increases along with the size of fluoroalkane moiety. Unfortunately, the analysis and quantitative estimation of interatomic interactions using only analysis of short contacts is difficult and ambiguous. To provide more information about the role of intermolecular interactions into crystal packing energy quantum chemical calculations were carried out using different DFT functionals and basis sets (PBE/800 eV and CE-B3LYP/6-31G(d,p)).

3.2. Quantum Chemical Calculations of Crystal Structures 1–4

The bond lengths obtained in PBE calculations of crystal structures 1–4 and isolated molecules of (CHF2)(CF2)nCH2OTs is in satisfactory agreement with experimental values. Root-mean-square deviations between experimental and calculated coordinates of non-hydrogen atoms are 0.032 (1), 0.035 (2a), 0.032 (2b, molecule A), 0.038 (2b, molecule B), 0.048 (3a), 0.055 (3b), and 0.043(4) Å. The differences in values of S-O, S-C and C-F bonds are 0.01–0.03 Å. The C-H bonds are elongated up to 0.12 Å, however, it is expected because the coordinates of hydrogen atoms cannot be measured with sufficient accuracy using X-ray diffraction. Intermolecular distances between non-hydrogen atoms somewhat changed, as compared to X-ray structures of studied compounds. Fortunately, the deviation between the calculated and the experimental structure are not so pronounced, therefore we can expect that the values related to the energies of intermolecular interactions from PBE-D3 calculations are valid for analysis of crystal packing.
Among the computational methods for analysis of intermolecular interactions the most popular and informative approach is R. Bader’s quantum theory of “Atoms in Molecules” (QTAIM) [37]. According to QTAIM any intermolecular contact can be detected by topological analysis of electron density function calculated for non-periodic (molecules or molecular associates) and periodic systems like crystals or surfaces. Analysis of calculated electron density in terms of QTAIM has shown that bond critical points (bcp) were found for all expected covalent bonds. The bcps related to bonds formed by sulfur atoms is characterized by positive value of Laplacian of ρ(r) (∇ρ(r)) and negative one of local energy density (He(r)) that indicate its highly polar character. The rest of bonds in studied structures can be described as typical covalent ones because the values of ∇ρ(r) and He(r) are negative.
Intermolecular interactions found by QTAIM analysis correspond to closed shell interactions (positive values of ∇ρ(r) and He(r) in corresponding bcps). It is noteworthy, that some types of interactions are not possible to detect on the base of structure analysis. For instance, QTAIM analysis revealed the presence of H…H, C–H…π and F…π interactions between methylene, phenyl and fluoroalkyl groups. The strongest intermolecular bonds are C–H…O hydrogen bonds between difluoromethyl and sulfonate moieties. Their energies raised along with the size of fluoroalkyl fragment from 5.8 kJ/mol in the case of CF2CHF2 group (2a) up to 12.3 kJ/mol in 4 ((CF2)7CHF2). In 2b the hydrogen atom of CHF2 group in molecule A formed bifurcate C–H…O and C–H…F bonds (8.7 and 5.9 kJ/mol) with sulfonate group of adjacent molecule A and CHF2 one of molecule B. The hydrogen atom of CHF2 group in molecule B participates only in C–H…F bond (4.9 kJ/mol) with difluoromethyl moiety of molecule A. In polymorphs of TsOCH2(CF2)5CHF2 the energies of present C–H…F bond differ by several kJ/mol (10.1 and 13.2 in 3a and 3b, respectively). In 1 where CHF2 group is changed to CF3 one the strongest intermolecular interaction is the C–H…O bond between a phenyl ring and a sulfonate moiety (7.8 kJ/mol). As rule, C–H…F bonds are somewhat weaker than C–H…O ones, the strongest hydrogen bonds of such type do not exceed 8 kJ/mol. Few bcps were also found for F…C contacts that mainly correspond to F…π interaction between a fluorine atom and a phenyl group. In addition, F…O interactions were detected. Two latter types of interactions are very weak (less than 2 kJ/mol).
Bcps related to F…F contacts attract especial interest. Some of fluorine atoms are not involved in F…F interactions, while the others form up to four intra- and intermolecular interactions of this type. Intramolecular F…F interactions were revealed for structure 3a (Table 2). In 3b that is another conformer (Figure 5) and polymorph of TsOCH2(CF2)5CHF2 such strong intramolecular interactions between fluorine atoms were not found. In fact, numerous F…F interactions formed a framework responsible for arrangement of fluoroalkyl fragments. In contrast to F…C and F…O interactions the energies of F…F vary in wide range from 0.5 to 13 kJ/mol. The strongest F…F interactions (for instance F5…F7 in 4) appeared to be stronger than C–H…O hydrogen bonds. According to literature, the analysis of valence electron density or deformation electron density (Δρ) distribution in the region of shortest F…F contacts clearly demonstrated that a lone pair of fluorine atoms is directed toward the local depletion of electron density between electron pairs of another fluorine atom [38] (“peak-hole interaction”). QTAIM and Δρ maps are very comprehensive tools for unexperienced reader, however, these methods cannot be used to analyze the entire region related to F…F interaction. Complementary information on intermolecular bonding was obtained using NCI (non-covalent interaction) method [39,40] based on dimensionless RDG (reduced density gradient) function related to the magnitude of λ2 eigenvalue(signλ2rho). To make analysis interatomic interactions more comprehensive 3D isosurfaces of RDG function in the regions of these interactions were colored according to the sign of λ2 multiplied by ρ(r). Similarly to Δρ, NCI method can be used as indicator for redistribution of electron density as result of chemical bond formation. Moreover, NCI method is much more useful for weak intermolecular interactions than Δρ. Maxima of RDG can be described as analog of bcp, those presence in interatomic region is an indicative for corresponding interaction. The shape and the volume of above-mentioned maxima supply additional information on interatomic interactions. Additionally, it is important to analyze the sign of λ2. As rule, the maxima for rather strong intermolecular interactions like classic hydrogen bonds (O–H…O or N–H…O) are small and they have discoidal shape. The sign of λ2 is mainly negative that is an indicative for attractive nature of classic hydrogen bonds. On the contrary, the maxima for weak H…H interactions are characterized by rather large area and they had no definite shape. At the same time, the regions with positive sigh of λ2 are dominated over those with a negative sign of λ2.
Since a lot of F…F interactions were found in 1–4 it is important to analyze these interactions using NCI to find similarities and differences between weakest and strongest ones related to their nature. It is clear (Figure 9, Figure 10 and Figure 11) that strongest intra- and intermolecular F…F interactions are characterized by negative values of λ2 similarly to hydrogen bond C-H…O between sulfonate group and terminal CHF2 group. These regions are highlighted by blue or light blue color on Figure 10, Figure 11 and Figure 12. Thus, F…F interactions shown in Table 2 can be described as mostly attractive ones. At the same time, the values of signλ2rho for the majority of intermolecular F…F interactions are close to zero and the sign of λ2 varied from positive to negative (green color on Figure 10, Figure 11 and Figure 12), so it is very difficult to unambiguously describe them as attractive or repulsive.

3.3. Lattice Energies and the Role of F…F Interactions

The energies of intermolecular interactions calculated from ρ(r) provided the opportunity to qualitatively estimate the contribution of F…F ones to the energy of crystal packing. In fact, the latter value is the sum of the energies of all intermolecular interactions found. This way to calculate the energy related to molecular association is very attractive, however, there is at least one serious drawback. This problem is related to empirical character of EML correlation formula, so it was criticized by Spackman [41]. According to Reference [41] EML formula in most cases underestimated the energy of intermolecular interactions by substantial amount as compared to the method implemented to CrystalExplorer program (CE-B3LYP). Severe judgement about EML correlation were expressed in the paper by Kuznetsov [42]. On the other hand, according to other published articles the lattice energies calculated from EML correlation provided reasonable values that agreed with experimental sublimation heat [43,44,45]. Thus, the reference method for estimation of lattice energies is necessary to attest the results of QTAIM approach and EML correlation formula for compounds with fluorinated alkyl moieties. The CE-B3LYP method seems to be the most reliable and comprehensive method for calculation of intermolecular potentials available for crystallographers. As result of CE-B3LYP calculations the values of interactions of a target molecule with its neighbors in molecular cluster generated according to space group symmetry operations are provided. The calculation of the intermolecular energies demonstrated the similarity of crystal packing motifs in 1–4 (See supporting information (CrystalExplorer17 output) for details). The strongest intermolecular interactions are observed between fluoroalkyl fragments. It is clear that energies of above interactions are increased along with the size of fluoroalkyl fragments. The value of lattice energy can be easily calculated from the data on all intermolecular interactions in cluster. Unfortunately, we encountered unexpected work of CrystalExplorer17 in the case of two independent molecules (2b). It was impossible to calculate lattice energy for two independent molecules separately. The value obtained for two independent molecules as a whole (−173.8 kJ/mol) is not reliable because the interactions between them are neglected.
The information about lattice energies estimated from QTAIM/EML method and CE-B3LYP/6-31G(d,p) calculations is presented in Figure 12 and Figure 13.
It can be seen from Figure 13 that QTAIM/EML overestimated the lattice energy in all structures except for 2a. Nevertheless, both methods predicted that polymorph 3b is more stable than 3a. This result was also verified by comparison of total energies of 3a and 3b (total energy of the latter divided by Z is 2.47 kJ/mol larger than the former). The situation with polymorphs 2a and 2b is the same as in 3a and 3b. Molecules A and B have noticeably different values of lattice energy. If averaged value of lattice energies of molecules A and B (165.6 kJ/mol) was taken as measure of stability, then 2b is appeared to be more stable than 2a. The comparison of the total energies of 2a and 2b divided by Z also supports this conclusion (the difference is 1.35 kJ/mol). Total contributions related to the most prominent intermolecular interactions are shown at Figure 14. It is logically to assume that contribution of F…F interactions to lattice energy will increase along the amount of fluorine atoms, while the contribution of H…O interactions (namely C-H…O hydrogen bonds) will decrease. At first glance, the results of QTAIM/EML evaluations agree with this assumption but there are two exceptions. The first one is related to polymorphism, because the contribution of F…F interactions can vary due to way of molecular packing. The part related to F…F in 3a exceeds that in 3b, although, their absolute values are almost equal (78.4 and 76.2 kJ/mol). At the same time, the percentage of H…O interactions in 3a is less than in 3b. It is necessary to remind that polymorph 3b is more stable than 3a. Again, the situation with polymorphs 2a and 2b is the same. The contribution of F…F interactions to lattice energy in 2b is larger than in 2a. At the same time, the percentage of H…O and H…F interactions in 2b is considerably larger than in 2a case. Thus, H…O interactions can be the main factor that made polymorphs 2b and 3b more favorable than 3a and 3a ones. This conclusion is in agreement with recent paper by Saha [46]. The second exception is related to contribution of O…H interactions in the case of 1. There is no terminal CHF2 group in molecule of PhO2SOC2F5, so this group cannot participate in C–H…O bonds with phenyl group that explain so low contribution of H…O interactions. Various interactions formed by hydrogen atoms (C–H…π, H…H, H…C, denoted as “other” on Figure 14) are responsible for more than 30% of lattice energy in 1.

4. Conclusions

The analysis of intermolecular interactions has shown that the contribution of interactions formed by fluorine atoms almost linearly depends on its amount. All studied compounds contain only three oxygen atoms, however, the role of C-H…O bonds is prominent even in the case of 4 that contain sixteen fluorine atoms. The contribution of F…F interaction does not exceed 40% even in the case of 4. Possibly such a relatively small contribution of F…F interaction is related to its specific nature. Indeed, according to the results NCI and QTAIM analysis F…F interactions in 1–4 hardly can be described as attractive as weak hydrogen bonds. Indeed, there are several strong interactions of such type with apparently attractive character, however, their total energy is rather small as compared to those for analogous weak interactions. The comparison of lattice energies calculated for polymorphs 2a, 3a, 2b and 3b has shown that increase of F…F contribution do not lead to stabilization of crystal packing in contrast to intermolecular C-H…O that have mostly attractive nature. In other words, the lower contribution of F…F interactions to the total energy, the more stable a polymorph is.

Supplementary Materials

The following are available online at https://www.mdpi.com/2073-4352/9/5/242/s1, Crystallographic data: Table S1 Crystallographic data for 1–4, Figure S1. Molecular structure of 2b, Figure S2. Molecular structure of 3b. VASP output: Parameters of unit cell and optimized fractional coordinates, Table S2: Total energy of unit cell (OUTCAR file). Output of Crystal Explorer program, References.

Author Contributions

Conceptualization, writing—original draft preparation, review and editing—D.E.A. and A.A.K.; synthesis—A.V.L. and D.E.A.; X-ray diffraction studies and quantum chemical calculations—A.D.V.

Funding

Quantum chemical studies and the synthesis of 2–4 were supported by Russian Science Foundation (grant 18-73-00339). The synthesis of compound 1 was supported by Russian Foundation for Basic Research (grant no. 18-29-20102).

Acknowledgments

X-ray diffraction studies were performed with the support from Ministry of Science and Higher Education of the Russian Federation using the equipment of Center for molecule composition studies of INEOS RAS.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ahrens, L.; Bundschuh, M. Fate and effects of poly- and perfluoroalkyl substances in the aquatic environment: A Review: Fate and effects of polyfluoroalkyl and perfluoroalkyl substances. Environ. Toxicol. Chem. 2014, 33, 1921–1929. [Google Scholar] [CrossRef] [PubMed]
  2. Ospinal-Jiménez, M.; Pozzo, D.C. Structural analysis of protein denaturation with alkyl perfluorinated sulfonates. Langmuir 2012, 28, 17749–17760. [Google Scholar] [CrossRef]
  3. Rosholm, K.R.; Arouri, A.; Hansen, P.L.; González-Pérez, A.; Mouritsen, O.G. Characterization of fluorinated catansomes: A promising vector in drug-delivery. Langmuir 2012, 28, 2773–2781. [Google Scholar] [CrossRef] [PubMed]
  4. Krafft, M. Fluorocarbons and fluorinated amphiphiles in drug delivery and biomedical research. Adv. Drug Deliv. Rev. 2001, 47, 209–228. [Google Scholar] [CrossRef]
  5. Massi, L.; Guittard, F.; Géribaldi, S.; Levy, R.; Duccini, Y. Antimicrobial properties of highly fluorinated bis-ammonium salts. Int. J. Antimicrob. Agents 2003, 21, 20–26. [Google Scholar] [CrossRef]
  6. Luo, Z.; Shi, X.; Hu, Q.; Zhao, B.; Huang, M. Structural evidence of perfluorooctane sulfonate transport by human serum albumin. Chem. Res. Toxicol. 2012, 25, 990–992. [Google Scholar] [PubMed]
  7. Du, Z.; Deng, S.; Bei, Y.; Huang, Q.; Wang, B.; Huang, J.; Yu, G. Adsorption behavior and mechanism of perfluorinated compounds on various adsorbents—A Review. J. Hazard. Mater. 2014, 274, 443–454. [Google Scholar] [CrossRef] [PubMed]
  8. Wadekar, M.N.; Abezgaus, L.; Djanashvili, K.; Jager, W.F.; Mendes, E.; Picken, S.J.; Dganit, D. Supramolecular “leeks” of a fluorinated hybrid amphiphile that self-assembles into a disordered columnar phase. J. Phys. Chem. B 2013, 117, 2820–2826. [Google Scholar] [CrossRef] [PubMed]
  9. Prasanna, M.D.; Row, T.N.G. Weak interactions involving organic fluorine: analysis of structural motifs in flunazirine and haloperidol. J. Mol. Struct. 2001, 562, 55–61. [Google Scholar] [CrossRef]
  10. Choudhury, A.R.; Urs, U.K.; Guru Row, T.N.; Nagarajan, K. Weak interactions involving organic fluorine: a comparative study of the crystal packing in substituted isoquinolines. J. Mol. Struct. 2002, 605, 71–77. [Google Scholar] [CrossRef]
  11. Osuna, R.M.; Hernández, V.; Navarrete, J.T.L.; D’Oria, E.; Novoa, J.J. Theoretical evaluation of the nature and strength of the F···F intermolecular interactions present in fluorinated hydrocarbons. Theor. Chem. Acc. 2011, 128, 541–553. [Google Scholar] [CrossRef]
  12. Nayak, S.K.; Reddy, M.K.; Row, T.N.G.; Chopra, D. Role of hetero-halogen (F···X, X = Cl, Br, and I) or homo-halogen (X···X, X = F, Cl, Br, and I) interactions in substituted benzanilides. Cryst. Growth Des. 2011, 11, 1578–1596. [Google Scholar] [CrossRef]
  13. Prakash, G.K.S.; Wang, F.; Rahm, M.; Shen, J.; Ni, C.; Haiges, R.; Olah, G.A. On the nature of CH⋅⋅⋅FC interactions in hindered CF3C(sp3) bond rotations. Angew. Chem. Int. Ed. 2011, 50, 11761–11764. [Google Scholar] [CrossRef]
  14. Alkorta, I.; Elguero, J. Fluorine–fluorine interactions: NMR and AIM analysis. Struct. Chem. 2004, 15, 117–120. [Google Scholar] [CrossRef]
  15. Levina, E.O.; Chernyshov, I.Y.; Voronin, A.P.; Alekseiko, L.N.; Stash, A.I.; Vener, M.V. Solving the enigma of weak fluorine contacts in the solid state: A periodic dft study of fluorinated organic crystals. RSC Adv. 2019, 9, 12520–12537. [Google Scholar] [CrossRef]
  16. Omorodion, H.; Twamley, B.; Platts, J.A.; Baker, R.J. Further evidence on the importance of fluorous–fluorous interactions in supramolecular chemistry: a combined structural and computational study. Cryst. Growth Des. 2015, 15, 2835–2841. [Google Scholar] [CrossRef]
  17. Baker, R.J.; Colavita, P.E.; Murphy, D.M.; Platts, J.A.; Wallis, J.D. Fluorine–fluorine interactions in the solid state: an experimental and theoretical study. J. Phys. Chem. A 2012, 116, 1435–1444. [Google Scholar] [CrossRef] [PubMed]
  18. Yoshida, Y.; Sakakura, Y.; Aso, N.; Okada, S.; Tanabe, Y. Practical and efficient methods for sulfonylation of alcohols using Ts(Ms)Cl/Et3N and Catalytic Me3H·HCl as combined base: Promising alternative to traditional pyridine. Tetrahedron 1999, 55, 2183–2192. [Google Scholar] [CrossRef]
  19. Banerjee, S.; Vidya, V.M.; Savyasachi, A.J.; Maitra, U. Perfluoroalkyl bile esters: A new class of efficient gelators of organic and aqueous–Organic media. J. Mater. Chem. 2011, 21, 14693–14705. [Google Scholar] [CrossRef]
  20. Cohen, W.V. Nucleophilic substitution in fluoroalkyl sulfates, sulfonates, and related compounds. J. Org. Chem. 1961, 26, 4021–4026. [Google Scholar] [CrossRef]
  21. Shilin, S.; Florensova, O.; Chernov, N.; Voronkov, M. Alpha, alpha, omega-trihydro-alpha-halo perfluoroalkanes. Zhurnal Obshchei Khimii 1991, 61, 1838–1840. [Google Scholar]
  22. Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Crystallogr. 2015, A71, 3–8. [Google Scholar] [CrossRef]
  23. Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. 2015, C71, 3–8. [Google Scholar]
  24. Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
  25. Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
  26. Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
  27. Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
  28. Kresse, G.; Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  29. Moellmann, J.; Grimme, S. Importance of London dispersion effects for the packing of molecular crystals: A case study for intramolecular stacking in a Bis-thiophene derivative. Phys. Chem. Chem. Phys. 2010, 12, 8500. [Google Scholar] [CrossRef] [PubMed]
  30. Gonze, X.; Beuken, J.-M.; Caracas, R.; Detraux, F.; Fuchs, M.; Rignanese, G.-M.; Sindic, L.; Verstraete, M.; Zerah, G.; Jollet, F.; et al. First-principles computation of material properties: The ABINIT software project. Comput. Mater. Sci. 2002, 25, 478–492. [Google Scholar] [CrossRef]
  31. Otero-de-la-Roza, A.; Johnson, E.R.; Luaña, V. Critic2: A program for real-space analysis of quantum chemical interactions in solids. Comput. Phys. Commun. 2014, 185, 1007–1018. [Google Scholar] [CrossRef]
  32. Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
  33. Mackenzie, C.F.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer model energies and energy frameworks: Extension to metal coordination compounds, organic salts, solvates and open-shell systems. IUCrJ 2017, 4, 575–587. [Google Scholar] [CrossRef]
  34. Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge structural database. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 171–179. [Google Scholar] [CrossRef]
  35. Rowland, R.S.; Taylor, R. Intermolecular nonbonded contact distances in organic crystal structures: comparison with distances expected from van der Waals Radii. J. Phys. Chem. 1996, 100, 7384–7391. [Google Scholar] [CrossRef]
  36. Desiraju, G.R.; Parthasarathy, R. The nature of Halogen...Halogen interactions: Are short halogen contacts due to specific attractive forces or due to close packing of nonspherical atoms? J. Am. Chem. Soc. 1989, 111, 8725–8726. [Google Scholar] [CrossRef]
  37. Bader, R.W.F. Atoms in Molecules: A Quantum Theory; Oxford University Press: New York, NY, USA, 1990. [Google Scholar]
  38. Levin, V.V.; Dilman, A.D.; Korlyukov, A.A.; Belyakov, P.A.; Struchkova, M.I.; Antipin, M.Yu.; Tartakovsky, V.A. Synthesis and structures of tris(pentafluorophenyl)silylamines. Russ. Chem. Bull. 2007, 56, 1394–1401. [Google Scholar] [CrossRef]
  39. Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing noncovalent interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef]
  40. Saleh, G.; Gatti, C.; Lo Presti, L. Non-covalent Interaction via the reduced density gradient: independent atom model vs experimental multipolar electron densities. Comput. Theor. Chem. 2012, 998, 148–163. [Google Scholar] [CrossRef]
  41. Spackman, M.A. How reliable are intermolecular interaction energies estimated from topological analysis of experimental electron densities? Cryst. Growth Des. 2015, 15, 5624–5628. [Google Scholar] [CrossRef]
  42. Kuznetsov, M.L. Can halogen bond energy be reliably estimated from electron density properties at bond critical point? The case of the (A)nZ—Y•••X − (X, Y = F, Cl, Br) interactions. Int. J. Quantum Chem. 2019, 119, e25869. [Google Scholar] [CrossRef]
  43. Nelyubina, Y.V.; Korlyukov, A.A.; Lyssenko, K.A. Probing weak intermolecular interactions by using the invariom approach: A comparative study of s-tetrazine. Chem. Eur. J. 2014, 6978–6984. [Google Scholar] [CrossRef] [PubMed]
  44. Nelyubina, Y.V.; Korlyukov, A.A.; Lyssenko, K.A. Probing systematic errors in experimental charge density by multipole and invariom modeling: A twinned crystal of 1,10-phenanthroline hydrate. Mendeleev Commun. 2014, 24, 286–289. [Google Scholar] [CrossRef]
  45. Lyssenko, K.A.; Korlyukov, A.A.; Golovanov, D.G.; Ketkov, S.Yu.; Antipin, M.Yu. Estimation of the barrier to rotation of benzene in the (η6-C6H6)2Cr crystal via topological analysis of the electron density distribution function. J. Phys. Chem. A 2006, 110, 6545–6551. [Google Scholar] [CrossRef]
  46. Saha, A.; Rather, S.A.; Sharada, D.; Saha, B.K. ’C–X···X–C vs C–H···X–C, which one is the more dominant interaction in crystal packing (X = Halogen)? Cryst. Growth Des. 2018, 18, 6084–6090. [Google Scholar] [CrossRef]
Crystals 09 00242 g001 550
Figure 1. Molecular structure of 1. Atoms are presented as thermal ellipsoids.
Figure 1. Molecular structure of 1. Atoms are presented as thermal ellipsoids.
Crystals 09 00242 g001
Crystals 09 00242 g002 550
Figure 2. Molecular structure of 2a. Atoms are presented as thermal ellipsoids.
Figure 2. Molecular structure of 2a. Atoms are presented as thermal ellipsoids.
Crystals 09 00242 g002
Crystals 09 00242 g003 550
Figure 3. Overlaid molecules in structures 2a and 2b. Color code: 2b, molecule A—magenta; 2a, molecule B—blue; and 2a is colored by element.
Figure 3. Overlaid molecules in structures 2a and 2b. Color code: 2b, molecule A—magenta; 2a, molecule B—blue; and 2a is colored by element.
Crystals 09 00242 g003
Crystals 09 00242 g004 550
Figure 4. Molecular structure of 3a. Atoms are presented as thermal ellipsoids.
Figure 4. Molecular structure of 3a. Atoms are presented as thermal ellipsoids.
Crystals 09 00242 g004
Crystals 09 00242 g005 550
Figure 5. Overlaid molecular structures of polymorphs 3a (colored by element) and 3b (blue).
Figure 5. Overlaid molecular structures of polymorphs 3a (colored by element) and 3b (blue).
Crystals 09 00242 g005
Crystals 09 00242 g006 550
Figure 6. Molecular structure of 4. Atoms are presented as thermal ellipsoids.
Figure 6. Molecular structure of 4. Atoms are presented as thermal ellipsoids.
Crystals 09 00242 g006
Crystals 09 00242 g007 550
Figure 7. Crystal packing of 1 (a) and 4 (b).
Figure 7. Crystal packing of 1 (a) and 4 (b).
Crystals 09 00242 g007
Crystals 09 00242 g008 550
Figure 8. Crystal packing of polymorphs 2a (a) and 2b (b).
Figure 8. Crystal packing of polymorphs 2a (a) and 2b (b).
Crystals 09 00242 g008
Crystals 09 00242 g009 550
Figure 9. Crystal packing of polymorphs 3a (a) and 3b (b).
Figure 9. Crystal packing of polymorphs 3a (a) and 3b (b).
Crystals 09 00242 g009
Crystals 09 00242 g010 550
Figure 10. 3D surface of RDG (0.6 a.u.) colored according to sign(λ2)ρ function in 1 illustrating the interaction between CF3 groups.
Figure 10. 3D surface of RDG (0.6 a.u.) colored according to sign(λ2)ρ function in 1 illustrating the interaction between CF3 groups.
Crystals 09 00242 g010
Crystals 09 00242 g011 550
Figure 11. 3D surface of RDG (0.6 a.u.) colored according to sign (λ2) ρ function in 3a illustrating the interaction between (CF2)5CHF2 groups. Intermolecular interactions between fluorine atoms are shown at middle bottom.
Figure 11. 3D surface of RDG (0.6 a.u.) colored according to sign (λ2) ρ function in 3a illustrating the interaction between (CF2)5CHF2 groups. Intermolecular interactions between fluorine atoms are shown at middle bottom.
Crystals 09 00242 g011
Crystals 09 00242 g012 550
Figure 12. 3D surface of RDG (0.6 a.u.) colored according to sign (λ2) ρ function in 4 illustrating the interactions between (CF2)5CHF2 groups. Intermolecular C-H…O bond (1) and strong F…F interaction (2) are shown.
Figure 12. 3D surface of RDG (0.6 a.u.) colored according to sign (λ2) ρ function in 4 illustrating the interactions between (CF2)5CHF2 groups. Intermolecular C-H…O bond (1) and strong F…F interaction (2) are shown.
Crystals 09 00242 g012
Crystals 09 00242 g013 550
Figure 13. Calculated lattice energies in 1–4. The values are shown above the bars. Molecules A and B denoted as 2b-A and 2b-B. The values were multiplied by –1.
Figure 13. Calculated lattice energies in 1–4. The values are shown above the bars. Molecules A and B denoted as 2b-A and 2b-B. The values were multiplied by –1.
Crystals 09 00242 g013
Crystals 09 00242 g014 550
Figure 14. Relative contribution of various intermolecular interactions to lattice energy according QTAIM/EML.
Figure 14. Relative contribution of various intermolecular interactions to lattice energy according QTAIM/EML.
Crystals 09 00242 g014
Table
Table 1. Selected bond lengths and angles in 1–4.
Table 1. Selected bond lengths and angles in 1–4.
Structural Parameters (Å and °)Crystal Structure
12a2b3a3b4
S1-O11.5980(12)1.5896(12)1.5918(18)1.602(3)1.586(2)1.5900(14)
S1-O21.4238(14)1.4304(13)1.4284(19)1.438(3)1.425(2)1.4347(15)
S1-O31.4285(14)1.4276(13)1.4273(19)1.433(4)1.429(2)1.4298(15)
S1-C11.7474(17)1.7530(16)1.749(3)1.752(5)1.752(3)1.7584(19)
O1-C81.439(2)1.445(2)1.445(3)1.436(6)1.438(3)1.448(2)
C9-F1.353(2)1.356(2)1.358(3)1.360(5)1.356(3)1.357(2)
C-F *---1.348(6)1.344(3)1.345(2)
C-Fterm1.326(2)1.356(2)1.354(3)1.338(8)1.347(5)1.350(4)
O1-S1-C1103.65(8)103.97(7)104.04(11)103.6(2)103.08(12)103.32(8)
C8-O1-S1116.09(11)116.91(10)117.77(16)119.9(3)116.98(16)117.07(11)
* - mean C-F distance with exception of vicinal CF2 and terminal CHF2 groups.
Table
Table 2. Strongest F…F interactions in 1–4 estimated using the EML [32] correlation.
Table 2. Strongest F…F interactions in 1–4 estimated using the EML [32] correlation.
Interactions (Compound)Type
(Intramolecular/Intermolecular)		Experimental DistanceCalculated DistanceEnergy, kJ/mol
F4…F4 (1)intermolecular2.978(3)2.925−4.2
F3…F3 (2a)intermolecular2.750(2)2.785−5.9
F4…F4A (2b)intermolecular3.074(2)3.046−3.1
F3…F7 (3a)intramolecular2.633(5)2.649−12.2
F3…F8 (3a)intermolecular2.764(4)2.785−5.5
F5…F9 (3a)intramolecular2.582(5)2.620−4.6
F4…F7 (3b)intermolecular2.921(2)2.876−4.6
F5…F8 (3b)intermolecular2.543(3)2.572−10.5
F4…F11 (4)intermolecular2.9031(17)2.937−3.8
F4…F12 (4)intermolecular2.7953917)2.777−5.5
F5…F7 (4)intermolecular2.5112(17)2.507−13.0
F14…F14 (4)intermolecular2.942(3)2.895−5.0

Share and Cite

MDPI and ACS Style

Arkhipov, D.E.; Lyubeshkin, A.V.; Volodin, A.D.; Korlyukov, A.A. Molecular Structures Polymorphism the Role of F…F Interactions in Crystal Packing of Fluorinated Tosylates. Crystals 2019, 9, 242. https://doi.org/10.3390/cryst9050242

AMA Style

Arkhipov DE, Lyubeshkin AV, Volodin AD, Korlyukov AA. Molecular Structures Polymorphism the Role of F…F Interactions in Crystal Packing of Fluorinated Tosylates. Crystals. 2019; 9(5):242. https://doi.org/10.3390/cryst9050242

Chicago/Turabian Style

Arkhipov, Dmitry E., Alexander V. Lyubeshkin, Alexander D. Volodin, and Alexander A. Korlyukov. 2019. "Molecular Structures Polymorphism the Role of F…F Interactions in Crystal Packing of Fluorinated Tosylates" Crystals 9, no. 5: 242. https://doi.org/10.3390/cryst9050242

APA Style

Arkhipov, D. E., Lyubeshkin, A. V., Volodin, A. D., & Korlyukov, A. A. (2019). Molecular Structures Polymorphism the Role of F…F Interactions in Crystal Packing of Fluorinated Tosylates. Crystals, 9(5), 242. https://doi.org/10.3390/cryst9050242

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop