Quantifying Mg2+ Binding to ssDNA Oligomers: A Self-Consistent Field Theory Study at Varying Ionic Strengths and Grafting Densities
Abstract
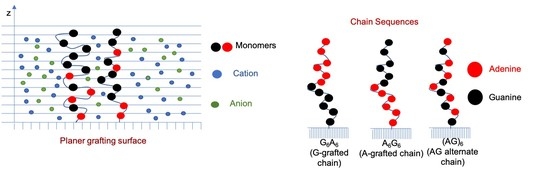
:1. Introduction
2. Theoretical Methodology
Extremization of the Free Energy
3. Results and Discussions
3.1. Effect of Sequence Heterogeneity on Mg Binding
3.2. Effect of Ionic Strength and Grafting Density
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Keefe, A.D.; Pai, S.; Ellington, A. Aptamers as therapeutics. Nat. Rev. Drug Discov. 2010, 9, 537. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Li, W.; Cai, T.; Deng, Y.; Ding, Z.; Liu, Y.; Zhu, X.; Wang, X.; Liu, J.; Liang, B. TiO2 Nanolayer-Enhanced Fluorescence for Simultaneous Multiplex Mycotoxin Detection by Aptamer Microarrays on a Porous Silicon Surface. ACS Appl. Mater. Interfaces 2018, 10, 14447–14453. [Google Scholar] [CrossRef] [PubMed]
- Cho, E.J.; Lee, J.-W.; Ellington, A.D. Applications of aptamers as sensors. Annu. Rev. Anal. Chem. 2009, 2, 241–264. [Google Scholar] [CrossRef] [PubMed]
- Dua, P.; Kang, S.; Shin, H.-S.; Kim, S.; Lee, D.-K. Cell-SELEX-Based Identification of a Human and Mouse Cross-Reactive Endothelial Cell-Internalizing Aptamer. Nucleic Acid Ther. 2018, 28. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.; Latchoumanin, O.; Hebbard, L.; Duan, W.; Liddle, C.; George, J.; Qiao, L. Aptamers as targeting ligands and therapeutic molecules for overcoming drug resistance in cancers. Adv. Drug Deliv. Rev. 2018, 134, 107–121. [Google Scholar] [CrossRef] [PubMed]
- Foster, A.; DeRosa, M.C. Development of a biocompatible layer-by-layer film system using aptamer technology for smart material applications. Polymers 2014, 6, 1631–1654. [Google Scholar] [CrossRef]
- Nakatsuka, N.; Yang, K.-A.; Abendroth, J.M.; Cheung, K.M.; Xu, X.; Yang, H.; Zhao, C.; Zhu, B.; Rim, Y.S.; Yang, Y. Aptamer–field-effect transistors overcome Debye length limitations for small-molecule sensing. Science 2018, 362, 319–324. [Google Scholar] [CrossRef] [PubMed]
- Uline, M.J.; Rabin, Y.; Szleifer, I. Effects of the salt concentration on charge regulation in tethered polyacid monolayers. Langmuir 2011, 27, 4679–4689. [Google Scholar] [CrossRef] [PubMed]
- Nap, R.J.; Szleifer, I. Effect of calcium ions on the interactions between surfaces end-grafted with weak polyelectrolytes. J. Chem. Phys. 2018, 149, 163309. [Google Scholar] [CrossRef] [PubMed]
- Nap, R.J.; Solveyra, E.G.; Szleifer, I. The interplay of nanointerface curvature and calcium binding in weak polyelectrolyte-coated nanoparticles. Biomater. Sci. 2018, 6, 1048–1058. [Google Scholar] [CrossRef] [PubMed]
- Zwanikken, J.W.; Guo, P.; Mirkin, C.A.; Olvera de la Cruz, M. Local ionic environment around polyvalent nucleic acid-functionalized nanoparticles. J. Phys. Chem. C 2011, 115, 16368–16373. [Google Scholar] [CrossRef]
- Kumar, R.; Sumpter, B.G.; Kilbey, S.M. Charge regulation and local dielectric function in planar polyelectrolyte brushes. J. Chem. Phys. 2012, 136, 234901. [Google Scholar] [CrossRef] [PubMed]
- Lewis, T.; Pandav, G.; Omar, A.; Ganesan, V. Complexation between weakly basic dendrimers and linear polyelectrolytes: effects of grafts, chain stiffness, and pOH. Soft Matter 2013, 9, 6955–6969. [Google Scholar] [CrossRef]
- Liu, J.; Cao, Z.; Lu, Y. Functional nucleic acid sensors. Chem. Rev. 2009, 109, 1948–1998. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Huang, P.-J.J.; Ding, J.; Liu, J. Aptamer-based biosensors for biomedical diagnostics. Analyst 2014, 139, 2627–2640. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-S.; Han, M.S.; Mirkin, C.A. Colorimetric detection of mercuric ion (Hg2+) in aqueous media using DNA-functionalized gold nanoparticles. Angew. Chem. Int. Ed. 2007, 46, 4093–4096. [Google Scholar] [CrossRef] [PubMed]
- Saenger, W. Principles of Nucleic Acid Structure; Springer: Berlin, Germany, 1984; pp. 201–219. [Google Scholar]
- Reshetnikov, R.V.; Sponer, J.; Rassokhina, O.I.; Kopylov, A.M.; Tsvetkov, P.O.; Makarov, A.A.; Golovin, A.V. Cation binding to 15-TBA quadruplex DNA is a multiple-pathway cation-dependent process. Nucleic Acids Res. 2011, 39, 9789–9802. [Google Scholar] [CrossRef] [PubMed]
- Ono, A.; Torigoe, H.; Tanaka, Y.; Okamoto, I. Binding of metal ions by pyrimidine base pairs in DNA duplexes. Chem. Soc. Rev. 2011, 40, 5855–5866. [Google Scholar] [CrossRef] [PubMed]
- Anastassopoulou, J.; Theophanides, T. Magnesium–DNA interactions and the possible relation of magnesium to carcinogenesis. Irradiation and free radicals. Critical Rev. Oncol./Hematol. 2002, 42, 79–91. [Google Scholar] [CrossRef]
- Pascal, A.; Grover, N.; Westhof, E. Metal ion binding to RNA. Met. Ions Life Sci. 2011, 9, 1–35. [Google Scholar]
- Mocci, F.; Laaksonen, A. Insight into nucleic acid counterion interactions from inside molecular dynamics simulations is ‘worth its salt’. Soft Matter 2012, 8, 9268–9284. [Google Scholar] [CrossRef]
- Murthy, C.S.; Bacquet, R.J.; Rossky, P.J. Ionic distributions near polyelectrolytes. A comparison of theoretical approaches. J. Phys. Chem. 1985, 89, 701–710. [Google Scholar] [CrossRef]
- Patra, C.N.; Yethiraj, A. Density functional theory for the distribution of small ions around polyions. J. Phys. Chem. B 1999, 103, 6080–6087. [Google Scholar] [CrossRef]
- Howard, J.J.; Lynch, G.C.; Pettitt, B.M. Ion and solvent density distributions around canonical B-DNA from integral equations. J. Phys. Chem. B 2010, 115, 547–556. [Google Scholar] [CrossRef] [PubMed]
- Hayes, R.L.; Noel, J.K.; Whitford, P.C.; Mohanty, U.; Sanbonmatsu, K.Y.; Onuchic, J.N. Reduced model captures Mg2+-RNA interaction free energy of riboswitches. Biophys. J. 2014, 106, 1508–1519. [Google Scholar] [CrossRef] [PubMed]
- Savelyev, A.; MacKerell, A.D., Jr. Competition among Li+, Na+, K+ and Rb+ monovalent ions for DNA in molecular dynamics simulations using the additive CHARMM36 and Drude polarizable force fields. J. Phys. Chem. B 2015, 119, 4428–4440. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Nordenskiöld, L.; Mu, Y. Sequence-Specific Mg2+ –DNA Interactions: A Molecular Dynamics Simulation Study. J. Phys. Chem. B 2011, 115, 14713–14720. [Google Scholar] [CrossRef] [PubMed]
- Gebala, M.; Bonilla, S.; Bisaria, N.; Herschlag, D. Does cation size affect occupancy and electrostatic screening of the nucleic acid ion atmosphere? J. Am. Chem. Soc. 2016, 138, 10925–10934. [Google Scholar] [CrossRef] [PubMed]
- Gebala, M.; Giambasu, G.M.; Lipfert, J.; Bisaria, N.; Bonilla, S.; Li, G.; York, D.M.; Herschlag, D. Cation–anion interactions within the nucleic acid ion atmosphere revealed by ion counting. J. Am. Chem. Soc. 2015, 137, 14705–14715. [Google Scholar] [CrossRef] [PubMed]
- Mills, P.; Anderson, C.F.; Record, M.T., Jr. Monte Carlo studies of counterion-DNA interactions. Comparison of the radial distribution of counterions with predictions of other polyelectrolyte theories. J. Phys. Chem. 1985, 89, 3984–3994. [Google Scholar] [CrossRef]
- Jacobson, D.R.; Saleh, O.A. Counting the ions surrounding nucleic acids. Nucleic Acids Res. 2016, 45, 1596–1605. [Google Scholar] [CrossRef] [PubMed]
- Holland, J.G.; Malin, J.N.; Jordan, D.S.; Geiger, F.M. Specific and Nonspecific Metal Ion- Nucleotide Interactions at Aqueous/Solid Interfaces Functionalized with Adenine, Thymine, Guanine, and Cytosine Oligomers. J. Am. Chem. Soc. 2011, 133, 2567–2570. [Google Scholar] [CrossRef] [PubMed]
- Holland, J.G.; Jordan, D.S.; Geiger, F.M. Divalent metal cation speciation and binding to surface-bound oligonucleotide single strands studied by second harmonic generation. J. Phys. Chem. B 2011, 115, 8338–8345. [Google Scholar] [CrossRef] [PubMed]
- Szleifer, I.; Carignano, M. Tethered polymer layers. Adv. Chem. Phys. Polym. Syst. 1996, 94, 165–260. [Google Scholar]
- Uline, M.J.; Meng, S.; Szleifer, I. Surfactant driven surface anchoring transitions in liquid crystal thin films. Soft Matter 2010, 6, 5482–5490. [Google Scholar] [CrossRef]
- Van der Munnik, N.P.; Sajib, M.S.J.; Moss, M.A.; Wei, T.; Uline, M.J. Determining the Potential of Mean Force for Amyloid-β Dimerization: Combining Self-Consistent Field Theory with Molecular Dynamics Simulation. J. Chem. Theory Comput. 2018, 14, 2696–2704. [Google Scholar] [CrossRef] [PubMed]
- Nap, R.J.; Park, S.H.; Szleifer, I. Competitive calcium ion binding to end-tethered weak polyelectrolytes. Soft Matter 2018, 14, 2365–2378. [Google Scholar] [CrossRef] [PubMed]
- Bloomfield, V.; Crothers, D.M. Nucleic Acids: Structures, Properties and Functions; No. 574.192 B52; Universidad Autónoma Chapingo: Texcoco, Mexico, 2000. [Google Scholar]
- Flory, P.J.; Volkenstein, M. Statistical Mechanics of Chain Molecules; Interscience: New York, NY, USA, 1969. [Google Scholar]
- Yu, J.; Mao, J.; Yuan, G.; Satija, S.; Jiang, Z.; Chen, W.; Tirrell, M. Structure of polyelectrolyte brushes in the presence of multivalent counterions. Macromolecules 2016, 49, 5609–5617. [Google Scholar] [CrossRef]
- Wu, T.; Gong, P.; Szleifer, I.; Vlcěk, P.; Šubr, V.; Genzer, J. Behavior of surface-anchored poly (acrylic acid) brushes with grafting density gradients on solid substrates: 1. Experiment. Macromolecules 2007, 40, 8756–8764. [Google Scholar] [CrossRef]
- Lee, Y.; Thirumalai, D.; Hyeon, C. Ultrasensitivity of water exchange kinetics to the size of metal ion. J. Am. Chem. Soc. 2017, 139, 12334–12337. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Greenfeld, M.; Travers, K.J.; Chu, V.B.; Lipfert, J.; Doniach, S.; Herschlag, D. Quantitative and comprehensive decomposition of the ion atmosphere around nucleic acids. J. Am. Chem. Soc. 2007, 129, 14981–14988. [Google Scholar] [CrossRef] [PubMed]










© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jahan, M.; Uline, M.J. Quantifying Mg2+ Binding to ssDNA Oligomers: A Self-Consistent Field Theory Study at Varying Ionic Strengths and Grafting Densities. Polymers 2018, 10, 1403. https://doi.org/10.3390/polym10121403
Jahan M, Uline MJ. Quantifying Mg2+ Binding to ssDNA Oligomers: A Self-Consistent Field Theory Study at Varying Ionic Strengths and Grafting Densities. Polymers. 2018; 10(12):1403. https://doi.org/10.3390/polym10121403
Chicago/Turabian StyleJahan, Merina, and Mark J. Uline. 2018. "Quantifying Mg2+ Binding to ssDNA Oligomers: A Self-Consistent Field Theory Study at Varying Ionic Strengths and Grafting Densities" Polymers 10, no. 12: 1403. https://doi.org/10.3390/polym10121403
APA StyleJahan, M., & Uline, M. J. (2018). Quantifying Mg2+ Binding to ssDNA Oligomers: A Self-Consistent Field Theory Study at Varying Ionic Strengths and Grafting Densities. Polymers, 10(12), 1403. https://doi.org/10.3390/polym10121403