Rheology of Concentrated Polymer/Ionic Liquid Solutions: An Anomalous Plasticizing Effect and a Universality in Nonlinear Shear Rheology
Abstract
:1. Introduction
2. Experimental Section
2.1. Sample Information
2.2. Preparation of Polymer/IL Solutions
2.3. Rheological Measurement
3. Linear Viscoelasticity
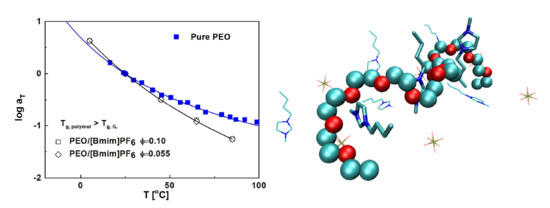
3.1. PEO/IL Solutions
3.2. PMMA/IL Solutions
4. Nonlinear Viscoelasticity
4.1. Start-up Measurement
4.2. Nonlinear Stress Relaxation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Lodge, T.P.; Ueki, T. Mechanically tunable, readily processable ion gels by self-assembly of block copolymers in ionic liquids. Acc. Chem. Res. 2016, 49, 2107–2114. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, J.; Chang, L.; Zhang, X.; Liu, H.; Jiang, L. Preparation of high-performance ionogels with excellent transparency, good mechanical strength, and high conductivity. Adv. Mater. 2017, 29, 1704253. [Google Scholar] [CrossRef]
- Gu, Y.Y.; Cussler, E.L.; Lodge, T.P. ABA-triblock copolymer ion gels for CO2 separation applications. J. Membr. Sci. 2012, 423, 20–26. [Google Scholar] [CrossRef]
- Ranjbaran, F.; Kamio, E.; Matsuyama, H. Inorganic/organic composite ion gel membrane with high mechanical strength and high CO2 separation performance. J. Membr. Sci. 2017, 544, 252–260. [Google Scholar] [CrossRef]
- Ranjbaran, F.; Kamio, E.; Matsuyama, H. Ion gel membrane with tunable inorganic/organic composite network for CO2 separation. Ind. Eng. Chem. Res. 2017, 56, 12763–12772. [Google Scholar] [CrossRef]
- Moghadam, F.; Kamio, E.; Matsuyama, H. High CO2 separation performance of amino acid ionic liquid-based double network ion gel membranes in low CO2 concentration gas mixtures under humid conditions. J. Membr. Sci. 2017, 525, 290–297. [Google Scholar] [CrossRef]
- Moghadam, F.; Kamio, E.; Yoshizumi, A.; Matsuyama, H. An amino acid ionic liquid-based tough ion gel membrane for CO2 capture. Chem. Commun. 2015, 51, 13658–13661. [Google Scholar] [CrossRef] [PubMed]
- Kasahara, S.; Kamio, E.; Yoshizumi, A.; Matsuyama, H. Polymeric ion-gels containing an amino acid ionic liquid for facilitated CO2 transport media. Chem. Commun. 2014, 50, 2996–2999. [Google Scholar] [CrossRef]
- Moon, H.C.; Lodge, T.P.; Frisbie, C.D. Solution-processable electrochemiluminescent ion gels for flexible, low-voltage, emissive displays on plastic. J. Am. Chem. Soc. 2014, 136, 3705–3712. [Google Scholar] [CrossRef]
- Xie, Z.L.; Huang, X.; Taubert, A. Dyeionogels: Proton-responsive ionogels based on a dye-ionic liquid exhibiting reversible color change. Adv. Funct. Mater. 2014, 24, 2837–2843. [Google Scholar] [CrossRef]
- Noro, A.; Tomita, Y.; Shinohara, Y.; Sageshima, Y.; Walish, J.J.; Matsushita, Y.; Thomas, E.L. Photonic block copolymer films swollen with an ionic liquid. Macromolecules 2014, 47, 4103–4109. [Google Scholar] [CrossRef]
- Lee, J.; Kaake, L.G.; Cho, J.H.; Zhu, X.Y.; Lodge, T.P.; Frisbie, C.D. Ion gel-gated polymer thin-film transistors: Operating mechanism and characterization of gate dielectric capacitance, switching speed, and stability. J. Phys. Chem. C 2009, 113, 8972–8981. [Google Scholar] [CrossRef]
- Cho, J.H.; Lee, J.; Xia, Y.; Kim, B.; He, Y.Y.; Renn, M.J.; Lodge, T.P.; Frisbie, C.D. Printable ion-gel gate dielectrics for low-voltage polymer thin-film transistors on plastic. Nat. Mater. 2008, 7, 900–906. [Google Scholar] [CrossRef]
- Chopade, S.A.; So, S.; Hillmyer, M.A.; Lodge, T.P. Anhydrous proton conducting polymer electrolyte membranes via polymerization-induced microphase separation. ACS Appl. Mater. Interfaces 2016, 8, 6200–6210. [Google Scholar] [CrossRef]
- Pinkert, A.; Marsh, K.N.; Pang, S.; Staiger, M.P. Ionic liquids and their interaction with cellulose. Chem. Rev. 2009, 109, 6712–6728. [Google Scholar] [CrossRef]
- Liu, F.Y.; Lv, Y.X.; Liu, J.J.; Yan, Z.C.; Zhang, B.Q.; Zhang, J.; He, J.S.; Liu, C.Y. Crystallization and rheology of poly(ethylene oxide) in imidazolium ionic liquids. Macromolecules 2016, 49, 6106–6115. [Google Scholar] [CrossRef]
- Kharel, A.; Lodge, T.P. Coil dimensions of poly(ethylene oxide) in an ionic liquid by small-angle neutron scattering. Macromolecules 2017, 50, 8739–8744. [Google Scholar] [CrossRef]
- Triolo, A.; Russina, O.; Keiderling, U.; Kohlbrecher, J. Morphology of poly(ethylene oxide) dissolved in a room temperature ionic liquid: A small angle neutron scattering study. J. Phys. Chem. B 2006, 110, 1513–1515. [Google Scholar] [CrossRef]
- Son, C.Y.; McDaniel, J.G.; Cui, Q.; Yethiraj, A. Conformational and dynamic properties of poly(ethylene oxide) in BMIM+BF4–: A microsecond computer simulation study using ab initio force fields. Macromolecules 2018, 51, 5336–5345. [Google Scholar] [CrossRef]
- Werzer, O.; Warr, G.G.; Atkin, R. Conformation of poly(ethylene oxide) dissolved in ethylammonium nitrate. J. Phys. Chem. B 2011, 115, 648–652. [Google Scholar] [CrossRef]
- Smith, J.A.; Webber, G.B.; Warr, G.G.; Zimmer, A.; Atkin, R.; Werzer, O. Shear dependent viscosity of poly(ethylene oxide) in two protic ionic liquids. J. Colloid Interface Sci. 2014, 430, 56–60. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; FitzGerald, P.A.; Warr, G.G.; Atkin, R. Conformation of poly(ethylene oxide) dissolved in the solvate ionic liquid [Li(G4)]TFSI. Phys. Chem. Chem. Phys. 2015, 17, 14872–14878. [Google Scholar] [CrossRef] [PubMed]
- Mok, M.M.; Liu, X.C.; Bai, Z.F.; Lei, Y.; Lodge, T.P. Effect of concentration on the glass transition and viscoelastic properties of poly(methyl methacrylate)/ionic liquid solutions. Macromolecules 2011, 44, 1016–1025. [Google Scholar] [CrossRef]
- Mondal, J.; Choi, E.; Yethiraj, A. Atomistic simulations of poly(ethylene oxide) in water and an ionic liquid at room temperature. Macromolecules 2014, 47, 438–446. [Google Scholar] [CrossRef]
- McDaniel, J.G.; Choi, E.; Son, C.Y.; Schmidt, J.R.; Yethiraj, A. Conformational and dynamic properties of poly(ethylene oxide) in an ionic liquid: Development and implementation of a first-principles force field. J. Phys. Chem. B 2016, 120, 231–243. [Google Scholar] [CrossRef]
- Costa, L.T.; Ribeiro, M.C.C. Molecular dynamics simulation of polymer electrolytes based on poly(ethylene oxide) and ionic liquids. I. Structural properties. J. Chem. Phys. 2006, 124, 184902. [Google Scholar] [CrossRef]
- Tsuda, R.; Kodama, K.; Ueki, T.; Kokubo, H.; Imabayashi, S.-I.; Watanabe, M. LCST-type liquid-liquid phase separation behaviour of poly(ethylene oxide) derivatives in an ionic liquid. Chem. Commun. 2008, 40, 4939–4941. [Google Scholar] [CrossRef]
- Lee, H.N.; Lodge, T.P. Unusual lower critical solution temperature phase behavior of poly(ethylene oxide) in ionic liquids. Macromolecules 2012, 45, 3627–3633. [Google Scholar] [CrossRef]
- Asai, H.; Fujii, K.; Nishi, K.; Sakai, T.; Ohara, K.; Umebayashi, Y.; Shibayama, M. Solvation structure of poly(ethylene glycol) in ionic liquids studied by high-energy X-ray diffraction and molecular dynamics simulations. Macromolecules 2013, 46, 2369–2375. [Google Scholar] [CrossRef]
- Xiao, Z.L.; Larson, R.G.; Chen, Y.L.; Zhou, C.T.; Niu, Y.H.; Li, G.X. Unusual phase separation and rheological behavior of poly(ethylene oxide)/ionic liquid mixtures with specific interactions. Soft Matter 2016, 12, 7613–7623. [Google Scholar] [CrossRef]
- Huang, Q.; Mednova, O.; Rasmussen, H.K.; Alvarez, N.J.; Skov, A.L.; Almdal, K.; Hassager, O. Concentrated polymer solutions are different from melts: Role of entanglement molecular weight. Macromolecules 2013, 46, 5026–5035. [Google Scholar] [CrossRef]
- Huang, Q.; Alvarez, N.J.; Matsumiya, Y.; Rasmussen, H.K.; Watanabe, H.; Hassager, O. Extensional rheology of entangled polystyrene solutions suggests importance of nematic interactions. ACS Macro Lett. 2013, 2, 741–744. [Google Scholar] [CrossRef]
- Costanzo, S.; Huang, Q.; Ianniruberto, G.; Marrucci, G.; Hassager, O.; Vlassopoulos, D. Shear and extensional rheology of polystyrene melts and solutions with the same number of entanglements. Macromolecules 2016, 49, 3925–3935. [Google Scholar] [CrossRef]
- Ianniruberto, G. Extensional flows of solutions of entangled polymers confirm reduction of friction coefficient. Macromolecules 2015, 48, 6306–6312. [Google Scholar] [CrossRef]
- Ianniruberto, G.; Brasiello, A.; Marrucci, G. Simulations of fast shear flows of PS oligomers confirm monomeric friction reduction in fast elongational flows of monodisperse PS melts as indicated by rheooptical data. Macromolecules 2012, 45, 8058–8066. [Google Scholar] [CrossRef]
- Yan, Z.-C.; Zhang, B.-Q.; Liu, C.-Y. Dynamics of concentrated polymer solutions revisited: Isomonomeric friction adjustment and its consequences. Macromolecules 2014, 47, 4460–4470. [Google Scholar] [CrossRef]
- Fetters, L.J.; Lohse, D.J.; Colby, R.H. Chain dimensions and entanglement spacings. In Physical Properties of Polymers Handbook, 2nd ed.; Mark, J.E., Ed.; Springer: New York, NY, USA, 2007; pp. 447–454. [Google Scholar]
- Zhang, S.J.; Sun, N.; He, X.Z.; Lu, X.M.; Zhang, X.P. Physical properties of ionic liquids: Database and evaluation. J. Phys. Chem. Ref. Data 2006, 35, 1475–1517. [Google Scholar] [CrossRef]
- Lungwitz, R.; Strehmel, V.; Spange, S. The dipolarity/polarisability of 1-alkyl-3-methylimidazolium ionic liquids as function of anion structure and the alkyl chain length. New J. Chem. 2010, 34, 1135–1140. [Google Scholar] [CrossRef]
- Chiappe, C.; Malvaldi, M.; Pomelli, C.S. Ionic liquids: Solvation ability and polarity. Pure Appl. Chem. 2009, 81, 767–776. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; Wiley: New York, NY, USA, 1980. [Google Scholar]
- Almeida, H.F.D.; Canongia Lopes, J.N.; Rebelo, L.P.N.; Coutinho, J.A.P.; Freire, M.G.; Marrucho, I.M. Densities and viscosities of mixtures of two ionic liquids containing a common cation. J. Chem. Eng. Data 2016, 61, 2828–2843. [Google Scholar] [CrossRef]
- Fetters, L.J.; Lohse, D.J.; Richter, D.; Witten, T.A.; Zirkel, A. Connection between polymer molecular-weight, density, chain dimensions, and melt viscoelastic properties. Macromolecules 1994, 27, 4639–4647. [Google Scholar] [CrossRef]
- Tao, H.; Huang, C.; Lodge, T.P. Correlation length and entanglement spacing in concentrated hydrogenated polybutadiene solutions. Macromolecules 1999, 32, 1212–1217. [Google Scholar] [CrossRef]
- Colby, R.H.; Rubinstein, M. 2-parameter scaling for polymers in theta-solvents. Macromolecules 1990, 23, 2753–2757. [Google Scholar] [CrossRef]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Graessley, W.W. Polymeric Liquids and Networks: Dynamics and Rheology; Garland Science: New York, NY, USA, 2008. [Google Scholar]
- van Ruymbeke, E.; Masubuchi, Y.; Watanabe, H. Effective value of the dynamic dilution exponent in bidisperse linear polymers: From 1 to 4/3. Macromolecules 2012, 45, 2085–2098. [Google Scholar] [CrossRef]
- Kapnistos, M.; Vlassopoulos, D.; Roovers, J.; Leal, L.G. Linear rheology of architecturally complex macromolecules: Comb polymers with linear backbones. Macromolecules 2005, 38, 7852–7862. [Google Scholar] [CrossRef]
- McLeish, T.C.B.; Allgaier, J.; Bick, D.K.; Bishko, G.; Biswas, P.; Blackwell, R.; Blottiere, B.; Clarke, N.; Gibbs, B.; Groves, D.J.; et al. Dynamics of entangled H-polymers: Theory, rheology, and neutron-scattering. Macromolecules 1999, 32, 6734–6758. [Google Scholar] [CrossRef]
- Snijkers, F.; Vlassopoulos, D.; Lee, H.; Yang, J.; Chang, T.; Driva, P.; Hadjichristidis, N. Start-up and relaxation of well-characterized comb polymers in simple shear. J. Rheol. 2013, 57, 1079–1100. [Google Scholar] [CrossRef] [Green Version]
- Van Ruymbeke, E.; Orfanou, K.; Kapnistos, M.; Iatrou, H.; Pitsikalis, M.; Hadjichristidis, N.; Lohse, D.; Vlassopoulos, D. Entangled dendritic polymers and beyond: Rheology of symmetric cayley-tree polymers and macromolecular self-assemblies. Macromolecules 2007, 40, 5941–5952. [Google Scholar] [CrossRef]
- Niedzwiedz, K.; Wischnewski, A.; Pyckhout-Hintzen, W.; Allgaier, J.; Richter, D.; Faraone, A. Chain dynamics and viscoelastic properties of poly(ethylene oxide). Macromolecules 2008, 41, 4866–4872. [Google Scholar] [CrossRef]
- Maranas, J.K. The effect of environment on local dynamics of macromolecules. Curr. Opin. Colloid Interface Sci. 2007, 12, 29–42. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Yan, Z.C.; Wang, W. Dynamics of polymers in concentrated solutions: A weaker self-concentration effect. Polymer 2018, 153, 33–42. [Google Scholar] [CrossRef]
- Xu, W.; Cooper, E.I.; Angell, C.A. Ionic liquids: Ion mobilities, glass temperatures, and fragilities. J. Phys. Chem. B 2003, 107, 6170–6178. [Google Scholar] [CrossRef]
- Colby, R.H.; Fetters, L.J.; Funk, W.G.; Graessley, W.W. Effects of concentration and thermodynamic interaction on the viscoelastic properties of polymer-solutions. Macromolecules 1991, 24, 3873–3882. [Google Scholar] [CrossRef]
- Bruce, P.G.; Vincent, C.A. Polymer electrolytes. J. Chem. Soc. Faraday Trans. 1993, 89, 3187–3203. [Google Scholar] [CrossRef]
- Lin, K.-J.; Maranas, J.K. Cation coordination and motion in a poly(ethylene oxide)-based single ion conductor. Macromolecules 2012, 45, 6230–6240. [Google Scholar] [CrossRef]
- Cowie, J.M.G.; Martin, A.C.S.; Firth, A.-M. Ionic conductivity in mixtures of salts with comb-shaped polymers based on ethylene oxide macromers. Br. Polym. J. 1988, 20, 247–252. [Google Scholar] [CrossRef]
- Mos, B.; Verkerk, P.; Pouget, S.; van Zon, A.; Bel, G.J.; de Leeuw, S.W.; Eisenbach, C.D. The dynamics in polyethyleneoxide-alkali iodide complexes investigated by neutron spin-echo spectroscopy and molecular dynamics simulations. J. Chem. Phys. 2000, 113, 4–7. [Google Scholar] [CrossRef]
- Fullerton-Shirey, S.K.; Maranas, J.K. Effect of LiClO4 on the structure and mobility of PEO-based solid polymer electrolytes. Macromolecules 2009, 42, 2142–2156. [Google Scholar] [CrossRef]
- Mao, G.M.; Perea, R.F.; Howells, W.S.; Price, D.L.; Saboungi, M.-L. Relaxation in polymer electrolytes on the nanosecond timescale. Nature 2000, 405, 163–165. [Google Scholar] [CrossRef]
- Triolo, A.; Arrighi, V.; Triolo, R.; Passerini, S.; Mastragostino, M.; Lechner, R.E.; Ferguson, R.; Borodin, O.; Smith, G.D. Dynamic heterogeneity in polymer electrolytes. Comparison between QENS data and MD simulations. Phys. B Condens. Matter 2001, 301, 163–167. [Google Scholar] [CrossRef]
- Carlsson, P.; Zorn, R.; Andersson, D.; Farago, B.; Howells, W.S.; Borjesson, L. The segmental dynamics of a polymer electrolyte investigated by coherent quasielastic neutron scattering. J. Chem. Phys. 2001, 114, 9645–9656. [Google Scholar] [CrossRef] [Green Version]
- MacCallum, J.R.; Vincent, C.A. Polymer Electrolyte Reviews; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1989; Volume 2. [Google Scholar]
- Tarascon, J.-M.; Armand, M. Issues and challenges facing rechargeable lithium batteries. Nature 2001, 414, 359–367. [Google Scholar] [CrossRef]
- Tarascon, J.-M.; Gozdz, A.S.; Schmutz, C.; Shokoohi, F.; Warren, P.C. Performance of Bellcore’s plastic rechargeable Li-ion batteries. Solid State Ion. 1996, 86-88, 49–54. [Google Scholar] [CrossRef]
- Whittingham, M.S.; Savinell, R.F.; Zawodzinski, T. Introduction: Batteries and fuel cells. Chem. Rev. 2004, 104, 4243–4244. [Google Scholar] [CrossRef]
- Harun, F.; Chan, C.H.; Guo, Q. Rheology and microscopic heterogeneity of poly(ethylene oxide) solid polymer electrolytes. Macromol. Symp. 2017, 376, 1700040. [Google Scholar] [CrossRef]
- Goldansaz, H.; Auhl, D.; Goderis, B.; Voleppe, Q.; Fustin, C.-A.; Gohy, J.-F.; Bailly, C.; van Ruymbeke, E. Transient metallosupramolecular networks built from entangled melts of poly(ethylene oxide). Macromolecules 2015, 48, 3746–3755. [Google Scholar] [CrossRef]
- Lodge, T.P.; McLeish, T.C.B. Self-concentrations and effective glass transition temperatures in polymer blends. Macromolecules 2000, 33, 5278–5284. [Google Scholar] [CrossRef]
- Savin, D.A.; Larson, A.M.; Lodge, T.P. Effect of composition on the width of the calorimetric glass transition in polymer-solvent and solvent-solvent mixtures. J. Polym. Sci. B Polym. Phys. 2004, 42, 1155–1163. [Google Scholar] [CrossRef]
- Lipson, J.E.G.; Milner, S.T. Multiple glass transitions and local composition effects on polymer solvent mixtures. J. Polym. Sci. B Polym. Phys. 2006, 44, 3528–3545. [Google Scholar] [CrossRef] [Green Version]
- Salaniwal, S.; Kant, R.; Colby, R.H.; Kumar, S.K. Computer simulations of local concentration variations in miscible polymer blends. Macromolecules 2002, 35, 9211–9218. [Google Scholar] [CrossRef]
- Haley, J.C.; Lodge, T.P.; He, Y.Y.; Ediger, M.D.; von Meerwall, E.D.; Mijovic, J. Composition and temperature dependence of terminal and segmental dynamics in polyisoprene/poly(vinylethylene) blends. Macromolecules 2003, 36, 6142–6151. [Google Scholar] [CrossRef]
- Colby, R.H. Breakdown of time-temperature superposition in miscible polymer blends. Polymer 1989, 30, 1275–1278. [Google Scholar] [CrossRef]
- Chen, Q.; Matsumiya, Y.; Masubuchi, Y.; Watanabe, H.; Inoue, T. Component dynamics in polyisoprene/poly(4-tert-butylstyrene) miscible blends. Macromolecules 2008, 41, 8694–8711. [Google Scholar] [CrossRef]
- Cox, W.P.; Merz, E.H. Correlation of dynamic and steady flow viscosities. J. Polym. Sci. 1958, 28, 619–622. [Google Scholar] [CrossRef]
- Gleissle, W. Rheology, Vol. 2: Fluids; Astarita, G., Marrucci, G., Nicolais, L., Eds.; Plenum: New York, NY, USA, 1980. [Google Scholar]
- Auhl, D.; Ramirez, J.; Likhtman, A.E.; Chambon, P.; Fernyhough, C. Linear and nonlinear shear flow behavior of monodisperse polyisoprene melts with a large range of molecular weights. J. Rheol. 2008, 52, 801–835. [Google Scholar] [CrossRef]
- Schweizer, T.; van Meerveld, J.; Ottinger, H.C. Nonlinear shear rheology of polystyrene melt with narrow molecular weight distribution-experiment and theory. J. Rheol. 2004, 48, 1345–1364. [Google Scholar] [CrossRef]
- Snijkers, F.; Vlassopoulos, D. Cone-partitioned-plate geometry for the ares rheometer with temperature control. J. Rheol. 2011, 55, 1167–1186. [Google Scholar] [CrossRef]
- Yan, Z.C.; Costanzo, S.; Jeong, Y.; Chang, T.; Vlassopoulos, D. Linear and nonlinear shear rheology of a marginally entangled ring polymer. Macromolecules 2016, 49, 1444–1453. [Google Scholar] [CrossRef]
- Chen, X.; Liang, S.; Wang, S.-W.; Colby, R.H. Linear viscoelastic response and steady shear viscosity of native cellulose in 1-ethyl-3-methylimidazolium methylphosphonate. J. Rheol. 2018, 62, 81–87. [Google Scholar] [CrossRef]
- Kuang, Q.-L.; Zhao, J.-C.; Niu, Y.-H.; Zhang, J.; Wang, Z.-G. Celluloses in an ionic liquid: The rheological properties of the solutions spanning the dilute and semidilute regimes. J. Phys. Chem. B 2008, 112, 10234–10240. [Google Scholar] [CrossRef]
- Lu, F.; Song, J.; Cheng, B.-W.; Ji, X.-J.; Wang, L.-J. Viscoelasticity and rheology in the regimes from dilute to concentrated in cellulose 1-ethyl-3-methylimidazolium acetate solutions. Cellulose 2013, 20, 1343–1352. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Y.M.; Wang, H.P.; Wang, S.W.; Liang, S.W.; Colby, R.H. Solution rheology of cellulose in 1-butyl-3-methyl imidazolium chloride. J. Rheol. 2011, 55, 485–494. [Google Scholar] [CrossRef]
- Larson, R.G.; Sridhar, T.; Leal, L.G.; McKinley, G.H.; Likhtman, A.E.; McLeish, T.C.B. Definitions of entanglement spacing and time constants in the tube model. J. Rheol. 2003, 47, 809–818. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 4.—rheological properties. J. Chem. Soc. Faraday Trans. 1979, 75, 38–54. [Google Scholar] [CrossRef]
- Graham, R.S.; Likhtman, A.E.; McLeish, T.C.B.; Milner, S.T. Microscopic theory of linear, entangled polymer chains under rapid deformation including chain stretch and convective constraint release. J. Rheol. 2003, 47, 1171–1200. [Google Scholar] [CrossRef]
- Bent, J.; Hutchings, L.R.; Richards, R.W.; Gough, T.; Spares, R.; Coates, P.D.; Grillo, I.; Harlen, O.G.; Read, D.J.; Graham, R.S.; et al. Neutron-mapping polymer flow: Scattering, flow visualization, and molecular theory. Science 2003, 301, 1691–1695. [Google Scholar] [CrossRef]
- Graham, R.S.; Bent, J.; Hutchings, L.R.; Richards, R.W.; Groves, D.J.; Embery, J.; Nicholson, T.M.; McLeish, T.C.B.; Likhtman, A.E.; Harlen, O.G.; et al. Measuring and predicting the dynamics of linear monodisperse entangled polymers in rapid flow through an abrupt contraction. A small angle neutron scattering study. Macromolecules 2006, 39, 2700–2709. [Google Scholar] [CrossRef]
- Menezes, E.V.; Graessley, W.W. Nonlinear rheological behavior of polymer systems for several shear-flow histories. J. Polym. Sci. Polym. Phys. Ed. 1982, 20, 1817–1833. [Google Scholar] [CrossRef]
- Huang, Q.; Hengeller, L.; Alvarez, N.J.; Hassager, O. Bridging the gap between polymer melts and solutions in extensional rheology. Macromolecules 2015, 48, 4158–4163. [Google Scholar] [CrossRef]
- Haward, S.J.; Sharma, V.; Butts, C.P.; McKinley, G.H.; Rahatekar, S.S. Shear and extensional rheology of cellulose/ionic liquid solutions. Biomacromolecules 2012, 13, 1688–1699. [Google Scholar] [CrossRef]
- Liu, F.Y.; Zhang, B.Q.; Zhang, J.; Liu, C.Y. Rheological behaviors of sodium polystyrene sulfonate in 1-allyl-3-methylimidazolium chloride. Acta Polym. Sin. 2016, 1263–1272. [Google Scholar]
- Rolón-Garrido, V.H.; Wagner, M.H. The damping function in rheology. Rheol. Acta 2009, 48, 245–284. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Wiest, J.M.; Burdette, S.R.; Liu, T.W.; Bird, R.B. Effect of ring closure on rheological behavior. J. Non-Newton. Fluid Mech. 1987, 24, 279–295. [Google Scholar] [CrossRef]
- Kapnistos, M.; Kirkwood, K.M.; Ramirez, J.; Vlassopoulos, D.; Leal, L.G. Nonlinear rheology of model comb polymers. J. Rheol. 2009, 53, 1133–1153. [Google Scholar] [CrossRef]
- Osaki, K.; Takatori, E.; Kurata, M. Nonlinear viscoelasticity of semidilute polystyrene solutions-effect of molecular weight distribution. Macromolecules 1987, 20, 1681–1687. [Google Scholar] [CrossRef]
- Urakawa, O.; Takahashi, M.; Masuda, T.; Ebrahimi, N.G. Damping functions and chain relaxation in uniaxial and biaxial extensions: Comparison with the Doi-Edwards theory. Macromolecules 1995, 28, 7196–7201. [Google Scholar] [CrossRef]
- Venerus, D.C.; Brown, E.F.; Burghardt, W.R. The nonlinear response of a polydisperse polymer solution to step strain deformations. Macromolecules 1998, 31, 9206–9212. [Google Scholar] [CrossRef]













© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Wang, W.; Stadler, F.J.; Yan, Z.-C. Rheology of Concentrated Polymer/Ionic Liquid Solutions: An Anomalous Plasticizing Effect and a Universality in Nonlinear Shear Rheology. Polymers 2019, 11, 877. https://doi.org/10.3390/polym11050877
Liu Z, Wang W, Stadler FJ, Yan Z-C. Rheology of Concentrated Polymer/Ionic Liquid Solutions: An Anomalous Plasticizing Effect and a Universality in Nonlinear Shear Rheology. Polymers. 2019; 11(5):877. https://doi.org/10.3390/polym11050877
Chicago/Turabian StyleLiu, Zhonghua, Wei Wang, Florian J. Stadler, and Zhi-Chao Yan. 2019. "Rheology of Concentrated Polymer/Ionic Liquid Solutions: An Anomalous Plasticizing Effect and a Universality in Nonlinear Shear Rheology" Polymers 11, no. 5: 877. https://doi.org/10.3390/polym11050877
APA StyleLiu, Z., Wang, W., Stadler, F. J., & Yan, Z. -C. (2019). Rheology of Concentrated Polymer/Ionic Liquid Solutions: An Anomalous Plasticizing Effect and a Universality in Nonlinear Shear Rheology. Polymers, 11(5), 877. https://doi.org/10.3390/polym11050877