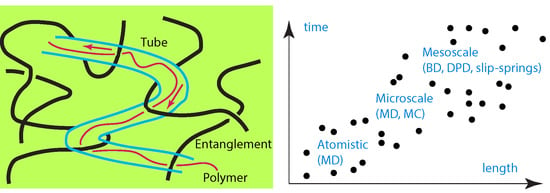
Modeling of Entangled Polymer Diffusion in Melts and Nanocomposites: A Review
Abstract
:1. Introduction
2. Experiments
2.1. Polymer Melts
2.2. Nanocomposites
3. Atomistic Simulations
3.1. Polymer Melts
3.2. Polymers Confined between Surfaces
4. Coarse-Grained Simulations
4.1. Molecular Dynamics
4.1.1. Polymer Melts
Polymer Polydispersity
Polymer Semiflexibility
4.1.2. Nanocomposites
4.2. Monte Carlo
4.2.1. Polymer Melts
4.2.2. Nanocomposites
4.2.3. Polymers Confined between Surfaces
5. Mesoscale Simulation Methods
5.1. Dissipative Particle Dynamics
5.2. Slip-Springs
6. Theoretical Modeling
6.1. Polymer Melts
6.2. Nanocomposites
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vacatello, M. Chain dimensions in filled polymers: An intriguing problem. Macromolecules 2002, 35, 8191–8193. [Google Scholar] [CrossRef]
- Allegra, G.; Raos, G.; Vacatello, M. Theories and simulations of polymer-based nanocomposites: From chain statistics to reinforcement. Prog. Polym. Sci. 2008, 33, 683–731. [Google Scholar] [CrossRef]
- Vacatello, M. Predicting the molecular arrangements in polymer-based nanocomposites. Macromol. Theory Simul. 2003, 12, 86–91. [Google Scholar] [CrossRef]
- Ganesan, V.; Jayaraman, A. Theory and simulation studies of effective interactions, phase behavior and morphology in polymer nanocomposites. Soft Matter 2014, 10, 13–38. [Google Scholar] [CrossRef]
- Karatrantos, A.; Clarke, N.; Composto, R.J.; Winey, K.I. Structure, entanglements and dynamics of polymer nanocomposites containing spherical nanoparticles. IOP Conf. Ser. Mater. Sci. Eng 2014, 64, 012041. [Google Scholar] [CrossRef] [Green Version]
- Karatrantos, A.; Composto, R.J.; Winey, K.I.; Clarke, N. Primitive path network, structure and dynamics of SWCNT/polymer nanocomposites. IOP Conf. Ser. Mater. Sci. Eng. 2012, 40, 012027. [Google Scholar] [CrossRef]
- Karatrantos, A.; Clarke, N.; Kröger, M. Modeling of polymer structure and conformations in polymer nanocomposites from atomistic to mesoscale: A Review. Polym. Rev. 2016, 56, 385–428. [Google Scholar] [CrossRef]
- Sharaf, M.A.; Mark, J.E. Monte Carlo simulations on the effects of nanoparticles on chain deformations and reinforcement in amorphous polyethylene networks. Polymer 2004, 45, 3943–3952. [Google Scholar] [CrossRef]
- Yuan, Q.W.; Kloczkowski, A.; Mark, J.E.; Sharaf, M.A. Simulations on the reinforcement of poly(dimethylsiloxane) elastomers by randomly distributed filler particles. J. Polym. Sci. Polym. Phys. Ed. 1996, 34, 1647–1657. [Google Scholar] [CrossRef]
- Liu, J.; Wu, S.; Zhang, L.; Wang, W.; Cao, D. Molecular dynamics simulation for insight into microscopic mechanism of polymer reinforcement. Phys. Chem. Chem. Phys. 2011, 13, 518–529. [Google Scholar] [CrossRef]
- Everaers, R.; Sukumaran, S.K.; Grest, G.S.; Svaneborg, C.; Sivasubramanian, A.; Kremer, K. Rheology and microscopic topology of entangled polymeric liquids. Science 2004, 303, 823–826. [Google Scholar] [CrossRef]
- Foteinopoulou, K.; Karayiannis, N.C.; Laso, M.; Kröger, M.; Mansfield, M.L. Universal scaling, entanglements, and knots of model chain molecules. Phys. Rev. Lett. 2008, 101, 265702. [Google Scholar] [CrossRef]
- Hoy, R.S.; Grest, G.S. Entanglements of an End-Grafted Polymer brush in a polymeric matrix. Macromolecules 2007, 40, 8389–8395. [Google Scholar] [CrossRef]
- Li, Y.; Kröger, M.; Liu, W.K. Nanoparticle effect on the dynamics of polymer chains and their entanglement network. Phys. Rev. Lett. 2012, 109, 118001. [Google Scholar] [CrossRef] [PubMed]
- Karatrantos, A.; Clarke, N.; Composto, R.J.; Winey, K.I. Entanglements in polymer nanocomposites containing spherical nanoparticles. Soft Matter 2016, 12, 2567–2574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, S.K.; Krishnamoorti, R. Nanocomposites: Structure, phase behavior, and properties. Annu. Rev. Chem. Biomol. Eng. 2010, 1, 37–58. [Google Scholar] [CrossRef] [PubMed]
- Kalathi, J.T.; Grest, G.S.; Kumar, S.K. Universal viscosity behavior of polymer nanocomposites. Phys. Rev. Lett. 2012, 109, 198301. [Google Scholar] [CrossRef]
- Li, Y.; Kröger, M.; Liu, W.K. Nanoparticle geometrical effect on structure, dynamics and anisotropic viscosities of polyethylene nanocomposites. Macromolecules 2012, 45, 2099–2112. [Google Scholar] [CrossRef]
- Crosby, A.J.; Lee, J.Y. Polymer nanocomposites: The nano effect on mechanical properties. Polym. Rev. 2007, 47, 217–229. [Google Scholar] [CrossRef]
- Li, Y.; Abberton, B.C.; Kröger, M.; Liu, W.K. Challenges in multiscale modeling of polymer dynamics. Polymers 2013, 5, 751–832. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1989. [Google Scholar]
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 1—Brownian motion in the equilibrium state. J. Chem. Soc. Faraday Trans. 2 1978, 74, 1789–1801. [Google Scholar] [CrossRef]
- Klein, J. Evidence for reptation in an entangled polymer melt. Nature 1978, 271, 143–145. [Google Scholar] [CrossRef]
- Leger, L.; Hervet, H.; Auroy, P.; Boucher, E.; Massey, G. The reptation model: Tests through diffusion measurements in linear polymer melts. Rheol. Ser. 1996, 5, 1–16. [Google Scholar]
- Viovy, J.L.; Rubinstein, M.; Colby, R.H. Constraint release in polymer melts: Tube reorganization versus tube dilation. Macromolecules 1991, 24, 3587–3596. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Mavrantzas, V.G.; Theodorou, D.N.; Kröger, M.; Ramirez, J.; Ottinger, H.C.; Vlassopoulos, D. Crossover from the Rouse to the entangled polymer melt regime: Signals from long, detailed atomistic molecular dynamics simulations, supported by rheological experiments. Macromolecules 2003, 36, 1376–1387. [Google Scholar] [CrossRef]
- Kröger, M.; Loose, W.; Hess, S. Structural changes and rheology of polymer melts via nonequilibrium molecular dynamics. J. Rheol. 1993, 37, 1057–1079. [Google Scholar] [CrossRef]
- Kröger, M.; Hess, S. Rheological evidence for a dynamical crossover in polymer melts via nonequilibrium molecular dynamics. Phys. Rev. Lett. 2000, 85, 1128–1131. [Google Scholar] [CrossRef] [PubMed]
- Stephanou, P.S.; Schweizer, T.; Kröger, M. Communication: Appearance of undershoots in start-up shear: Experimental findings captured by tumbling-snake dynamics. J. Chem. Phys. 2017, 146, 161101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cho, S.; Jeong, S.; Kim, J.M.; Baig, C. Molecular dynamics for linear polymer melts in bulk and confined systems under shear flow. Sci. Rep. 2017, 7, 9004. [Google Scholar] [CrossRef] [Green Version]
- Schleger, P.; Farago, B.; Lartigue, C.; Kollmar, A.; Richter, D. Clear evidence of reptation in polyethylene from neutron spin-echo spectroscopy. Phys. Rev. Lett. 1998, 81, 124–127. [Google Scholar] [CrossRef]
- Richter, D.; Willner, L.; Zirkel, A.; Farago, B.; Fetters, L.; Huang, J. Polymer motion at the crossover from Rouse to reptation dynamics. Macromolecules 1994, 27, 7437–7446. [Google Scholar] [CrossRef]
- Gold, B.; Pyckhout-Hintzen, W.; Wischnewski, A.; Radulescu, A.; Monkenbusch, M.; Allgaier, J.; Hoffmann, I.; Parisi, D.; Vlassopoulos, D.; Richter, D. Direct assessment of tube dilation in entangled polymers. Phys. Rev. Lett. 2019, 122, 088001. [Google Scholar] [CrossRef]
- De Gennes, P.G. Reptation of a polymer chain in the presence of fixed obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- Read, D. Calculation of scattering from stretched copolymers using the tube model: Incorporation of the effect of elastic inhomogeneities. Macromolecules 2004, 37, 5065–5092. [Google Scholar] [CrossRef]
- Lin, C.C.; Parrish, E.; Composto, R.J. Macromolecule and particle dynamics in confined media. Macromolecules 2016, 49, 5755–5772. [Google Scholar] [CrossRef]
- Mills, P.J.; Green, P.F.; Palmstrom, C.J.; Mayer, J.W.; Kramer, E.J. Analysis of diffusion in polymers by forward recoil spectrometry. Appl. Phys. Lett. 1984, 45, 957. [Google Scholar] [CrossRef]
- Lodge, T.P. Reconciliation of the molecular weight dependence of diffusion and viscosity in entangled polymers. Phys. Rev. Lett. 1999, 83, 3218–3221. [Google Scholar] [CrossRef]
- Green, P.F.; Palmstrom, C.J.; Mayer, J.W.; Kramer, E.J. Limits of reptation in polymer melts. Phys. Rev. Lett. 1984, 53, 2145. [Google Scholar] [CrossRef]
- Mills, P.J.; Green, P.F.; Palmstrom, C.J.; Mayer, J.W.; Kramer, E.J. Polydispersity effects on diffusion in polymers: Concentration profiles of d-polystyrene measured by forward recoil spectrometry. J. Polym. Sci. Polym. Phys. Ed. 1986, 24, 1–9. [Google Scholar] [CrossRef]
- Green, P.F.; Palmstrom, C.J.; Mayer, J.W.; Kramer, E.J. Marker displacement measurements of polymer-polymer interdiffusion. Macromolecules 1985, 18, 501–507. [Google Scholar] [CrossRef]
- Green, P.F.; Kramer, E.J. Matrix effects on the diffusion of long polymer chains. Macromolecules 1986, 19, 1108. [Google Scholar] [CrossRef]
- Green, P.F.; Kramer, E.J. Temperature dependence of tracer diffusion coefficients in polystyrene. MRS 1986, 1, 202–204. [Google Scholar] [CrossRef]
- Antonietti, M.; Coutandin, J.; Sillescu, H. Critical chain lengths in polystyrene bulk diffusion. Macromolecules 1986, 19, 793. [Google Scholar] [CrossRef]
- Antonietti, M.; Fölsch, K.; Sillescu, H. Critical chain lengths in polystyrene bulk diffusion. Makromol. Chem. 1987, 188, 2317–2324. [Google Scholar] [CrossRef]
- Tead, S.F.; Kramer, E.J.; Hadziioannou, G.; Antonietti, M.; Sillescu, H.; Lutz, P.; Strazielle, C. Polymer Topology and Diffusion: A Comparison of Diffusion in Linear and Cyclic Macromolecules. Macromolecules 1992, 25, 3942–3947. [Google Scholar] [CrossRef]
- Antonietti, M.; Coutandin, J.; Sillescu, H. Chainlength and temperature-dependence of self-diffusion coefficients in polystyrene. Macromol. Chem. Rapid Commun. 1984, 5, 525–528. [Google Scholar] [CrossRef]
- Fleischer, G.; Appel, M. Chain length and temperature dependence of the self-diffusion of polyisoprene and polybutadiene in the melt. Macromolecules 1995, 28, 7281–7283. [Google Scholar] [CrossRef]
- Appel, M.; Fleischer, G. Investigation of the chain length dependence of self-diffusion of poly(dimethylsiloxane) and poly(ethylene oxide) in the melt with pulsed field gradient NMR. Macromolecules 1993, 26, 5520–5525. [Google Scholar] [CrossRef]
- Ozisik, R.; Zheng, J.; Dionne, P.J.; Picu, C.R.; Von Meerwall, D.E. NMR relaxation and pulsed-gradient diffusion study of polyethylene nanocomposites. J. Chem. Phys. 2005, 123, 134901. [Google Scholar] [CrossRef]
- Pearson, D.; Ver Strate, G.; von Meerwall, E.; Schilling, F. Viscosity and self-diffusion coefficient of linear polyethylene. Macromolecules 1987, 20, 1133–1141. [Google Scholar] [CrossRef]
- Tao, H.; Lodge, T.P.; von Meerwall, E.D. Diffusivity and viscosity of concentrated hydrogenated polybutadiene solutions. Macromolecules 2000, 33, 1747–1758. [Google Scholar] [CrossRef]
- Wang, S.Q. Chain dynamics in entangled polymers: Diffusion versus rheology and their comparison. J. Polym. Sci. B 2003, 41, 1589–1604. [Google Scholar] [CrossRef] [Green Version]
- Spiess, H.W. 50th anniversary perspective: The importance of NMR spectroscopy to macromolecular science. Macromolecules 2017, 50, 1761–1777. [Google Scholar] [CrossRef]
- Likhtman, A.E. Single-chain slip-link model of entangled polymers: Simultaneous description of neutron spin-echo, rheology, and diffusion. Macromolecules 2005, 38, 6128–6139. [Google Scholar] [CrossRef]
- Chavez, F.V.; Saalwachter, K. Time-Domain NMR observation of entangled polymer dynamics: Universal behavior of flexible homopolymers and applicability of the tube model. Macromolecules 2011, 44, 1549–1559. [Google Scholar] [CrossRef]
- Park, S.J.; Desai, P.S.; Chen, X.; Larson, R.G. Universal relaxation behavior of entangled 1,4-polybutadiene melts in the transition frequency region. Macromolecules 2015, 48, 4122–4131. [Google Scholar] [CrossRef]
- Trutschel, M.L.; Mordvinkin, A.; Furtado, F.; Willner, L.; Saalwächter, K. Time-domain NMR observation of entangled polymer dynamics: Focus on all tube-model regimes, chain center, and matrix effects. Macromolecules 2018, 51, 4108–4117. [Google Scholar] [CrossRef]
- Furtado, F.; Damron, J.; Trutschel, M.L.; Franz, C.; Schröter, K.; Ball, R.C.; Saalwächter, K.; Panja, D. NMR observations of entangled polymer dynamics: Focus on tagged chain rotational dynamics and confirmation from a simulation model. Macromolecules 2014, 47, 256–268. [Google Scholar] [CrossRef]
- Gordon, G.V.; Schmidt, R.G.; Quintero, M.; Benton, N.J.; Cosgrove, T.; Krukonis, V.J.; Williams, K.; Wetmore, P.M. Impact of polymer molecular weight on the dynamics of poly(dimethylsiloxane)-polysilicate nanocomposites. Macromolecules 2010, 43, 10132–10142. [Google Scholar] [CrossRef]
- Wang, S.; von Meerwall, E.D.; Wang, S.Q.; Halasa, A.; Hsu, W.L.; Zhou, J.P.; Quirk, R.P. Diffusion and rheology of binary polymer mixtures. Macromolecules 2004, 37, 1641–1651. [Google Scholar] [CrossRef]
- Schneider, G.J.; Nusser, K.; Willner, L.; Falus, P.; Richter, D. Dynamics of nanocomposites. Curr. Opin. Chem. Eng. 2017, 16, 65–77. [Google Scholar] [CrossRef]
- Choi, J.; Cargnello, M.; Murrey, C.B.; Clarke, N.; Winey, K.I.; Composto, R.J. Universal scaling of polymer diffusion in nanocomposites. ACS Macro Lett. 2013, 2, 485–490. [Google Scholar] [CrossRef]
- Gam, S.; Meth, J.S.; Zane, S.G.; Chi, C.; Wood, B.A.; Seitz, M.E.; Winey, K.I.; Clarke, N.; Composto, R.J. Macromolecules diffusion in a crowded polymer nanocomposite. Macromolecules 2011, 44, 3494. [Google Scholar] [CrossRef]
- Gam, S.; Meth, J.S.; Zane, S.G.; Chi, C.; Wood, B.A.; Winey, K.I.; Clarke, N.; Composto, R.J. Polymer Diffusion in a polymer nanocomposite: Effect of nanoparticle size and polydispersity. Soft Matter 2012, 8, 6512–6520. [Google Scholar] [CrossRef]
- Tung, W.S.; Griffin, P.J.; Meth, J.S.; Clarke, N.; Composto, R.J.; Winey, K.I. Temperature-dependent suppression of polymer diffusion in polymer nanocomposites. ACS Macro Lett. 2016, 5, 735–739. [Google Scholar] [CrossRef]
- Bailey, E.J.; Griffin, P.J.; Composto, R.J.; Winey, K.I. Multiscale dynamics of small, attractive nanoparticles and entangled polymers in polymer nanocomposites. Macromolecules 2019, 52, 2181–2188. [Google Scholar] [CrossRef]
- Mu, M.; Clarke, N.; Composto, R.J.; Winey, K.I. Polymer diffusion exhibits a minimum with increasing single-walled carbon nanotube concentration. Macromolecules 2009, 42, 7091–7097. [Google Scholar] [CrossRef]
- Mu, M.; Seitz, M.E.; Clarke, N.; Composto, R.J.; Winey, K. Polymer tracer diffusion exhibits a minimum in nanocomposites containing spherical nanoparticles. Macromolecules 2011, 44, 191–193. [Google Scholar] [CrossRef]
- Choi, K.I.; Kim, T.H.; Yuan, G.; Satija, S.K.; Koo, J. Dynamics of entangled polymers confined between graphene oxide sheets as studied by neutron reflectivity. ACS Macro Lett. 2017, 6, 819–823. [Google Scholar] [CrossRef]
- Miller, B.; Imel, A.D.; Holley, W.; Baskaran, D.; Dadmun, M.D. The Role of nanoparticle rigidity on the diffusion of linear polystyrene in a polymer nanocomposite. Macromolecules 2015, 48, 8369–8375. [Google Scholar] [CrossRef]
- Lange, F.; Judeinstein, P.; Franz, C.; Hartmann-Azanza, B.; Ok, S.; Steinhart, M.; Saalwachter, K. Large-scale diffusion of entangled polymers along nanochannels. Macromolecules 2015, 4, 561–565. [Google Scholar] [CrossRef]
- Shin, K.; Obukhov, S.; Chen, J.T.; Huh, J.; Hwang, Y.; Mok, S.; Dobriyal, P.; Thiyagarajan, P.; Russell, T.P. Enhanced mobility of confined polymers. Nat. Mater. 2007, 6, 961–965. [Google Scholar] [CrossRef] [PubMed]
- Tsalikis, D.G.; Koukoulas, T.; Mavrantzas, V.G.; Pasquino, R.; Vlassopoulos, D.; Pyckhout-Hintzen, W.; Wischnewski, A.; Monkenbusch, M.; Richter, D. Microscopic structure, conformation, and dynamics of ring and linear poly(ethylene oxide) melts from detailed atomistic molecular dynamics simulations: Dependence on chain length and direct comparison with experimental data. Macromolecules 2017, 50, 2565–2584. [Google Scholar] [CrossRef]
- Hur, K.; Jeong, C.; Winkler, R.G.; Lacevic, N.; Gee, R.H.; Yoon, D.Y. Chain dynamics of ring and linear polyethylene melts from molecular dynamics simulations. Macromolecules 2011, 44, 2311–2315. [Google Scholar] [CrossRef]
- Takahashi, K.Z.; Nishimura, R.; Yamato, N.; Yasuoka, K.; Masubuchi, Y. Onset of static and dynamic universality among molecular models of polymers. Sci. Rep. 2017, 7, 12379. [Google Scholar] [CrossRef] [Green Version]
- Kremer, K.; Grest, G.; Carmesin, I. Crossover from Rouse to reptation dynamics: A molecular-dynamics simulation. Phys. Rev. Lett. 1988, 61, 566–569. [Google Scholar] [CrossRef]
- Zhou, Q.; Larson, R.G. Direct calculation of the tube potential confining entangled polymers. Macromolecules 2006, 39, 6737–6743. [Google Scholar] [CrossRef]
- Wang, Z.; Larson, R.G. Constraint release in entangled binary blends of linear polymers: A molecular dynamics study. Macromolecules 2008, 41, 4945–4960. [Google Scholar] [CrossRef]
- Steinhauser, M.O.; Schneider, J.; Blumen, A. Simulating dynamic crossover behavior of semiflexible linear polymers in solution and in the melt. J. Chem. Phys. 2009, 130, 164902. [Google Scholar] [CrossRef]
- Ramos, J.; Vega, J.F.; Martinez-Salazaar, J. Assessment of entanglement features and dynamics from atomistic simulations and experiments in linear and short chain branched polyolefins. Soft Matter 2012, 8, 6256. [Google Scholar] [CrossRef]
- Takahashi, K.Z.; Nishimura, R.; Yasuoka, K.; Masubuchi, Y. Molecular Dynamics simulations for resolving scaling laws of polyethylene melts. Polymers 2017, 9, 24. [Google Scholar] [CrossRef]
- Tsolou, G.; Mavrantzas, V.G.; Theodorou, D.N. Detailed atomistic molecular dynamics simulation of cis-1,4-poly(butadiene). Macromolecules 2005, 38, 1478–1492. [Google Scholar] [CrossRef]
- Kritikos, G.; Sgouros, A.; Vogiatzis, G.G.; Theodorou, D.N. Molecular dynamics study of polyethylene under confinement. J. Phys. Conf. Ser. 2016, 738, 012012. [Google Scholar] [CrossRef]
- Smith, S.W.; Hall, C.K.; Freeman, B.D. Large-scale molecular dynamics study of entangled hard-chain fluids. Phys. Rev. Lett. 1995, 75, 1316. [Google Scholar] [CrossRef]
- Smith, S.W.; Hall, C.K.; Freeman, B.D. Molecular dynamics study of entangled hard-chain fluids. J. Chem. Phys. 1996, 104, 5616–5637. [Google Scholar] [CrossRef]
- Smith, S.W.; Hall, C.K.; Freeman, B.D.; McCormick, J.A. Self Diffusion Coefficients and Atomic Mean-Squared Displacements in Entangled Hard Chain Fluids. In Numerical Methods for Polymeric Systems; The IMA Volumes in Mathematics and Its Applications; Whittington, S.G., Ed.; Springer: New York, NY, USA, 1998; Volume 102, p. 203. [Google Scholar]
- Shanbhag, S. Estimating self-diffusion in polymer melts: How long is a long enough molecular simulation? Molec. Simul. 2016, 42, 162–172. [Google Scholar] [CrossRef]
- Shanbhag, S. Extraction of self-diffusivity in systems with nondiffusive short-time behavior. Phys. Rev. E 2013, 88, 042816. [Google Scholar] [CrossRef]
- Paul, W.; Binder, K.; Heermann, D.W.; Kremer, K. Dynamics of polymer solutions and melts. Reptation predictions and scaling of relaxation times. J. Chem. Phys. 1991, 95, 7726. [Google Scholar] [CrossRef]
- Pütz, M.; Kremer, K.; Grest, G.S. What is the entanglement length in a polymer melt? Europhys. Lett. 2000, 49, 735–741. [Google Scholar] [CrossRef] [Green Version]
- Harmandaris, V.A.; Kremer, K. Dynamics of polystyrene mmelts through hierarchical multiscale simulations. Macromolecules 2009, 42, 791–802. [Google Scholar] [CrossRef]
- Grest, G.S. Communication: Polymer entanglement dynamics: Role of attractive interactions. J. Chem. Phys. 2016, 145, 141101. [Google Scholar] [CrossRef] [Green Version]
- Baumgartner, A.; Ebert, U.; Schafer, L. Segment motion in the reptation model of polymer dynamics. II. Simulations. J. Stat. Phys. 1998, 50, 1375. [Google Scholar] [CrossRef]
- Likhtman, A.E.; Sukumaran, S.K.; Ramirez, J. Linear viscoelasticity from molecular dynamics simulation of entangled polymers. Macromolecules 2007, 40, 6748–6757. [Google Scholar] [CrossRef]
- Pestryaev, E.M. Comparison of various correlation times in polymer melts by molecular dynamics simulation. J. Phys. Conf. Ser. 2011, 324, 012031. [Google Scholar] [CrossRef]
- Hsu, H.P.; Kremer, K. Static and dynamic properties of large polymer melts in equilibrium. J. Chem. Phys. 2016, 144, 154907. [Google Scholar] [CrossRef] [Green Version]
- Salerno, K.M.; Agrawal, A.; Perahia, D.; Grest, G.S. Resolving dynamic properties of polymers through coarse-grained computational studies. Macromolecules 2016, 116, 058302. [Google Scholar] [CrossRef]
- Guenza, M.G. Localization of chain dynamics in entangled polymer melts. Phys. Rev. E 2014, 89, 052603. [Google Scholar] [CrossRef]
- Ebert, U.; Baumgartner, A.; Schafer, L. Short time behavior in de Gennes’ reptation model. Phys. Rev. Lett. 1997, 78, 1592–1595. [Google Scholar] [CrossRef]
- Sun, Q.; Faller, R. Crossover from unentangled to entangled dynamics in a systematically coarse-grained polystyrene melt. Macromolecules 2006, 39, 812–820. [Google Scholar] [CrossRef]
- Hou, J.X.; Svaneborg, C.; Everaers, R.; Grest, G.S. Stress relaxation in entangled polymer melts. Phys. Rev. Lett. 2010, 105, 068301. [Google Scholar] [CrossRef]
- Peters, B.L.; Salerno, K.M.; Agrawal, A.; Perahia, D.; Grest, G.S. Coarse-grained modeling of polyethylene melts: Effect on dynamics. J. Chem. Theory Comput. 2017, 13, 2890–2896. [Google Scholar] [CrossRef]
- Jabbari-Farouji, S. Static and dynamic scaling behavior of a polymer melt model with triple-well bending potential. J. Polym. Sci. B 2018, 56, 1376–1392. [Google Scholar] [CrossRef]
- Xia, W.; Song, J.; Jeong, C.; Hsu, D.D.; Phelan, F.R.; Douglas, J.F.; Keten, S. Energy-Renormalization for Achieving Temperature Transferable Coarse-Graining of Polymer Dynamics. Macromolecules 2017, 50, 8787–8796. [Google Scholar] [CrossRef] [PubMed]
- Xia, W.; Hansoge, N.K.; Xu, W.S.; Phelan, F.R.; Keten, S.; Douglas, J.F. Energy renormalization for coarse-graining polymers having different segmental structures. Sci. Adv. 2019, 5, eaav4683. [Google Scholar] [CrossRef] [PubMed]
- Peters, B.L.; Salerno, K.M.; Ge, T.; Perahia, D.; Grest, G.S. Effect of chain length dispersity on the mobility of entangled polymers. Phys. Rev. Lett. 2018, 121, 057802. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Mavrantzas, V.G.; Theodorou, D.N. Atomistic molecular dynamics simulation of polydisperse linear polyethylene melts. Macromolecules 1998, 31, 7934–7943. [Google Scholar] [CrossRef]
- Langeloth, M.; Masubuchi, Y.; Bohm, M.C.; Müller-Plathe, F. Reptation and constraint release dynamics in bidisperse polymer melts. J. Chem. Phys. 2014, 141, 194904. [Google Scholar] [CrossRef]
- Bulacu, M.; van der Giessen, E. Effect of bending and torsion rigidity on self-diffusion in polymer melts: A molecular-dynamics study. J. Chem. Phys. 2005, 123, 114901. [Google Scholar] [CrossRef] [Green Version]
- Bulacu, M.; van der Giessen, E. Molecular-dynamics simulation study of the glass transition in amorphous polymers with controlled chain stiffness. Phys. Rev. E 2007, 76, 011807. [Google Scholar] [CrossRef]
- Svaneborg, C.; Everaers, R. Characteristic time and length scales in Kremer-Grest bead-spring polymer melts as a function of chain stiffness. arXiv 2018, arXiv:1808.03503. [Google Scholar]
- Uchida, N.; Grest, G.S.; Everaers, R. Viscoelasticity and primitive path analysis of entangled polymer liquids: From F-actin to polyethylene. J. Chem. Phys. 2008, 128, 044902. [Google Scholar] [CrossRef] [Green Version]
- Groot, R.D. Mesoscale simulation of semiflexible chains. I. Endpoint distribution and chain dynamics. J. Chem. Phys. 2013, 138, 224903. [Google Scholar] [CrossRef] [PubMed]
- Frischknecht, A.L.; Milner, S.T. Diffusion with contour length fluctuations in linear polymer melts. Macromolecules 2000, 33, 5273–5277. [Google Scholar] [CrossRef]
- Padding, T.; Briels, W.J. Time and length scales of polymer melts studied by coarse-grained molecular dynamics simulations. J. Chem. Phys. 2002, 117, 925–943. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Zhang, H.; Huang, X.W.; Huang, H.H.; Luo, M.B. Monte Carlo simulation on the dynamics of a semi-flexible polymer in the presence of nanoparticles. Phys. Chem. Chem. Phys. 2018, 20, 26333–26343. [Google Scholar] [CrossRef] [PubMed]
- Karatrantos, A.; Composto, R.J.; Winey, K.I.; Clarke, N. Polymer and spherical nanoparticle diffusion in nanocomposites. J. Chem. Phys. 2017, 146, 203331. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Picu, R.C.; Rakshit, A. Dynamics of free chains in polymer nanocomposites. J. Chem. Phys. 2007, 126, 144909. [Google Scholar] [CrossRef]
- Li, S.J.; Qian, H.J.; Lu, Z.Y. Translational and rotational dynamics of an ultra-thin nanorod probe particle in linear polymer melts. Phys. Chem. Chem. Phys. 2018, 20, 20996–21007. [Google Scholar] [CrossRef] [PubMed]
- Desai, T.; Keblinski, P.; Kumar, S.K. Molecular dynamics simulations of polymer transport in nanocomposites. J. Chem. Phys. 2005, 122, 134910. [Google Scholar] [CrossRef]
- Meyer, H.; Kreer, T.; Cavallo, A.; Wittmer, J.P.; Baschnagel, J. On the dynamics and disentanglement in thin and two-dimensional polymer films. Eur. Phys. J. Spec. Top. 2007, 141, 167–172. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wei, D.; Han, C.C.; Liao, Q. Dynamics of polymer melts confined by smooth walls: Crossover from nonentangled region to entangled region. J. Chem. Phys. 2007, 126, 204907. [Google Scholar] [CrossRef] [PubMed]
- Sussman, D.; Tung, W.S.; Winey, K.I.; Schweizer, K.S.; Riggleman, R.A. Entanglement reduction and anisotropic chain and primitive path conformations in polymer melts under thin film and cylindrical confinement. Macromolecules 2014, 47, 6462. [Google Scholar] [CrossRef]
- Tung, W.S.; Composto, R.J.; Riggleman, R.A.; Winey, K.I. Local polymer dynamics and diffusion in cylindrical nanoconfinement. Macromolecules 2015, 48, 2324–2332. [Google Scholar] [CrossRef]
- Pressly, J.F.; Riggleman, R.A.; Winey, K.I. Polymer diffusion is fastest at intermediate levels of cylindrical confinement. Macromolecules 2018, 51, 9789–9797. [Google Scholar] [CrossRef]
- Zhang, T.; Riggleman, R.A.; Winey, K.I. Polymer conformations and dynamics under confinement with two length scales. Macromolecules 2019, 52, 217–226. [Google Scholar] [CrossRef]
- Rubinstein, M. Discretized model of entangled-polymer dynamics. Phys. Rev. Lett. 1987, 59, 1946. [Google Scholar] [CrossRef]
- Deutsch, J.; Madden, T.L. The diffusion coefficient of a reptating polymer. J. Chem. Phys. 1989, 91, 3252. [Google Scholar] [CrossRef]
- Wittmer, J.; Paul, W.; Binder, K. Rouse and reptation dynamics at finite temperature: A Monte Carlo Simulation. Macromolecules 1992, 25, 7211–7219. [Google Scholar] [CrossRef]
- Kreer, T.; Baschnagel, J.; Müller, M.; Binder, K. Monte Carlo simulation of long chain polymer melts: Crossover from Rouse and reptation dynamics. Macromolecules 2001, 34, 1105–1117. [Google Scholar] [CrossRef]
- Carmesin, I.; Kremer, K. The bond fluctuation method: A new effective algorithm for the dynamics of polymers in all spatial dimensions. Macromolecules 1988, 21, 2819–2823. [Google Scholar] [CrossRef]
- Kremer, K.; Binder, K. Monte Carlo simulation of lattice models for macromolecules. Comput. Phys. Rep. 1988, 7, 259–310. [Google Scholar] [CrossRef]
- Paul, W.; Binder, K.; Heermann, D.W.; Kremer, K. Crossover scaling in semidilute polymer solutions: A Monte Carlo test. J. Phys. II 1991, 1, 37–60. [Google Scholar] [CrossRef]
- Kolinski, A.; Skolnick, J.; Yaris, R. Monte Carlo studies on the long time dynamic properties of dense cubic lattice multichain systems. I. The homopolymeric melt. J. Chem. Phys. 1987, 86, 7164–7173. [Google Scholar] [CrossRef]
- Kolinski, A.; Skolnick, J.; Yaris, R. Does reptation describe the dynamics of entangled, finite length polymer systems? A model simulation. J. Chem. Phys. 1987, 86, 1567–1585. [Google Scholar] [CrossRef]
- Lin, H.; Mattice, W.L.; Von Meerwall, E.D. Dynamics of polyethylene melts studied by Monte Carlo simulations on a high coordination lattice. J. Polym. Sci. B 2006, 44, 2556. [Google Scholar] [CrossRef]
- Shaffer, J.S. Effects of chain topology on polymer dynamics: Bulk melts. J. Chem. Phys. 1994, 101, 4205. [Google Scholar] [CrossRef]
- Muthukumar, M.; Baumgartner, A. Effects of entropic barriers on polymer dynamics. Macromolecules 1989, 22, 1937–1941. [Google Scholar] [CrossRef]
- Muthukumar, M.; Baumgartner, A. Diffusion of a polymer chain in random media. Macromolecules 1989, 22, 1941–1946. [Google Scholar] [CrossRef]
- Reiter, J. A random walk chain reptating in a network of obstacles: Monte Carlo study of diffusion and decay of correlations and a comparison with the Rouse and reptation models. J. Chem. Phys. 1991, 94, 3222. [Google Scholar] [CrossRef]
- Azuma, R.; Takayama, H. Diffusion of single long polymers in fixed and low density matrix of obstacles confined to two dimensions. J. Chem. Phys. 1999, 111, 8666–8671. [Google Scholar] [CrossRef] [Green Version]
- Dionne, P.J.; Osizik, R.; Picu, C.R. Structure and dynamics of polyethylene nanocomposites. Macromolecules 2005, 38, 9351–9358. [Google Scholar] [CrossRef]
- Termonia, Y. Chain confinement in polymer nanocomposites and its effect on polymer bulk properties. J. Polym. Sci. B 2010, 48, 687–692. [Google Scholar] [CrossRef]
- Karatrantos, A.; Composto, R.J.; Winey, K.I.; Kröger, M.; Clarke, N. Entanglements and dynamics of polymer melts near a SWCNT. Macromolecules 2012, 45, 7274. [Google Scholar] [CrossRef]
- Tung, W.S.; Clarke, N.; Composto, R.J.; Winey, K.I. Temperature dependence of polymer diffusion in MWCNT/PS nanocomposites. Macromolecules 2013, 46, 2317–2322. [Google Scholar] [CrossRef]
- Li, S.J.; Chen, Q.Y.; Ding, M.M.; Shi, T.F. Effect of bidispersity on dynamics of confined polymer films. Polymers 2018, 10, 1327. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: San Diego, CA, USA, 1996. [Google Scholar]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 1992, 19, 155. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Vacatello, M. Phantom chain simulations of polymer-nanofiller systems. Macromolecules 2003, 36, 3411–3416. [Google Scholar] [CrossRef]
- Vacatello, M. Phantom chain simulations of realisticaly sized polymer-based nanocomposites. Macromol. Theory Simul. 2006, 15, 303–310. [Google Scholar] [CrossRef]
- Spenley, N.A. Scaling laws for polymers in dissipative particle dynamics. Europhys. Lett. 2000, 49, 534. [Google Scholar] [CrossRef]
- Lahmar, F.; Tzoumanekas, C.; Theodorou, D.N.; Rousseau, B. Onset of entanglements revisited. Dynamical analysis. Macromolecules 2009, 42, 7485–7494. [Google Scholar] [CrossRef]
- Holleran, S.P.; Larson, R.G. Using spring repulsions to model entanglement interactions in Brownian dynamics simulations of bead-spring chains. Rheol. Acta 2008, 47, 3–17. [Google Scholar] [CrossRef]
- Goujon, F.; Malfreyt, P.; Tildesley, D.J. Mesoscopic simulation of entanglements using dissipative particle dynamics: Application to polymer brushes. J. Chem. Phys. 2008, 129, 034902. [Google Scholar] [CrossRef]
- Goujon, F.; Malfreyt, P.; Tildesley, D.J. Mesoscopic simulation of entangled polymer brushes under shear: Compression and rheological properties. Macromolecules 2009, 42, 4310. [Google Scholar] [CrossRef]
- Yamanoi, M.; Pozo, O.; Maia, J.M. Linear and non-linear dynamics of entangled linear polymer melts by modified tunable coarse-grained level Dissipative Particle Dynamics. J. Chem. Phys. 2011, 135, 044904. [Google Scholar] [CrossRef]
- Sirk, T.W.; Sliozberg, Y.R.; Brennan, J.K.; Lisal, M.; Andzelm, J.W. An enhanced entangled polymer model for dissipative particle dynamics. J. Chem. Phys. 2012, 136, 134903. [Google Scholar] [CrossRef]
- Khai, S.; Yamanoi, M.; Maia, J. The Lowe-Andersen thermostat as an alternative to the dissipative particle dynamics in the mesoscopic simulation of entangled polymers. J. Chem. Phys. 2013, 138, 174903. [Google Scholar]
- Kumar, S.; Larson, R.G. Brownian dynamics simulations of flexible polymers with spring–spring repulsions. J. Chem. Phys. 2001, 114, 6937. [Google Scholar] [CrossRef]
- Pan, G.; Manke, C.W. Developments toward simulation of entangled polymer melts by dissipative particle dynamics. Int. J. Mod. Phys. B 2003, 17, 231. [Google Scholar] [CrossRef]
- Fan, L.L.; Liu, L. Coarse grain simulations of linear polymer melts for chain lengths near the reptation transition. IOP Conf. Ser. Mater. Sci. Eng. 2018, 369, 012017. [Google Scholar] [CrossRef] [Green Version]
- Mondello, M.; Grest, G.S. Viscosity calculations of n-alkanes by equilibrium molecular dynamics. J. Chem. Phys. 1997, 106, 9327–9336. [Google Scholar] [CrossRef]
- Nikunen, P.; Karttunen, M.; Vattulainen, I. Reptational dynamics in dissipative particle dynamics simulations of polymer melts. Phys. Rev. E 2007, 75, 036713. [Google Scholar] [CrossRef] [PubMed]
- Padding, T.; Briels, W.J. Uncrossability constraints in mesoscopic polymer melt simulations: Non-Rouse behavior of C120H242. J. Chem. Phys. 2001, 115, 2846–2859. [Google Scholar] [CrossRef]
- Padding, J.T.; Briels, W.J. Coarse-grained molecular dynamics simulations of polymer melts in transient and steady shear flow. J. Chem. Phys. 2003, 118, 10276–10286. [Google Scholar] [CrossRef]
- Liu, H.; Xue, Y.H.; Qian, H.J.; Lu, Z.Y.; Sun, C.C. A practical method to avoid bond crossing in two-dimensional dissipative particle dynamics simulations. J. Chem. Phys. 2008, 129, 024902. [Google Scholar] [CrossRef] [PubMed]
- Hoda, N.; Larson, R.G. Brownian dynamics simulations of single polymer chains with and without self-entanglements in theta and good solvents under imposed flow fields. J. Rheol. 2010, 54, 1061. [Google Scholar] [CrossRef]
- Zhu, Y.L.; Liu, H.; Lu, Z.Y. A highly coarse-grained model to simulate entangled polymer melts. J. Chem. Phys. 2012, 136, 144903. [Google Scholar] [CrossRef]
- Edwards, D.; Vilgis, T. The effect of entanglements in rubber elasticity. Polymer 1986, 27, 483–492. [Google Scholar] [CrossRef]
- Schieber, J.D.; Andreev, M. Entangled polymer dynamics in equilibrium and flow modelled through slip links. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 367–381. [Google Scholar] [CrossRef]
- Karatrantos, A.; Clarke, N.; Composto, R.J.; Winey, K.I. Topological entanglement length in polymer melts and nanocomposites by a DPD polymer model. Soft Matter 2013, 9, 3877–3884. [Google Scholar] [CrossRef]
- Hua, C.C.; Schieber, J.D. Segment connectivity, chain-length breathing, segmental stretch, and constraint release in reptation models. I. Theory and single-step strain predictions. J. Chem. Phys. 1998, 109, 10018. [Google Scholar] [CrossRef]
- Green, M.S.; Tobolsky, A.V. A New Approach to the Theory of Relaxing Polymeric Media. J. Chem. Phys. 1946, 14, 80. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Takimoto, J.I.; Koyama, K.; Ianniruberto, G.; Marrucci, G.; Grego, F. Brownian simulations of a network of reptating primitive chains. J. Chem. Phys. 2001, 115, 4387. [Google Scholar] [CrossRef]
- Doi, M.; Takimoto, J. Molecular modelling of entanglement. Phys. Trans. R. Soc. Lond. A 2003, 361, 641–652. [Google Scholar] [CrossRef]
- Nair, D.M.; Schieber, J.D. Linear viscoelastic predictions of a consistently unconstrained Brownian slip-link model. Macromolecules 2006, 39, 3386–3397. [Google Scholar] [CrossRef]
- Schieber, J.D.; Neergaard, J.; Gupta, S. A full-chain, temporary network model with sliplinks, chain-length fluctuations, chain connectivity and chain stretching. J. Rheol. 2003, 47, 213–233. [Google Scholar] [CrossRef]
- Rubinstein, M.; Panyukov, S. Elasticity of Polymer Networks. Macromolecules 2002, 35, 6670. [Google Scholar] [CrossRef]
- Masubuchi, Y. Contraction of Entangled Polymers After Large Step Shear Deformations in Slip-Link Simulations. Polymers 2019, 11, 370. [Google Scholar] [CrossRef] [PubMed]
- Masubuchi, Y.; Watanabe, H.; Ianniruberto, G.; Grego, F.; Marrucci, G. Comparison among Slip-Link Simulations of Bidisperse LinearPolymer Melts. Macromolecules 2008, 41, 8275. [Google Scholar] [CrossRef]
- Shanbhag, S. Fast Slip Link Model for Bidisperse Linear Polymer Melts. Macromolecules 2019, 52, 3092–3103. [Google Scholar] [CrossRef]
- Biondo, D.D.; Masnada, E.M.; Merabia, S.; Couty, M.; Barrat, J.L. Numerical study of a slip-link model for polymer melts and nanocomposites. J. Chem. Phys. 2013, 138, 194902. [Google Scholar] [CrossRef] [Green Version]
- Sen, S.; Kumar, S.K.; Keblinski, P. Viscoelastic properties of polymer melts from equilibrium molecular dynamics simulations. Macromolecules 2005, 38, 650–653. [Google Scholar] [CrossRef]
- Takahashi, K.Z.; Nishimura, R.; Yamato, N.; Yasuoka, K.; Masubuchi, Y. Critical test of bead-spring model to resolve the scaling laws of polymer melts: A molecular dynamics study. Mol. Simul. 2017, 43, 1196–1201. [Google Scholar] [CrossRef]
- Xu, X.; Chen, J.; An, L. Simulation studies on architecture dependence of unentangled polymer melts: A molecular dynamics study. J. Chem. Phys. 2015, 142, 074903. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Uneyama, T. Comparison among multi-chain models for entangled polymer dynamics. Soft Matter 2018, 14, 5986–5994. [Google Scholar] [CrossRef]
- Langeloth, M.; Masubuchi, Y.; Bohm, M.C.; Müller-Plathe, F. Recovering the reptation dynamics of polymer melts in dissipative particle dynamics via slip-springs. J. Chem. Phys. 2013, 138, 104907. [Google Scholar] [CrossRef] [PubMed]
- Uneyama, T.; Masubuchi, Y. Multi-chain slip-spring model for entangled polymer dynamics. J. Chem. Phys. 2012, 137, 154902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Megariotis, G.; Vogiatzis, G.G.; Sgouros, A.P.; Theodorou, D.N. Slip spring-based mesoscopic simulations of polymer networks: Methodology and the corresponding computational code. Polymers 2018, 10, 1156. [Google Scholar] [CrossRef]
- Sukumaran, S.K.; Likhtman, A.E. Modeling entangled dynamics: Comparison between stochastic single chain and multichain models. Macromolecules 2009, 42, 4300–4309. [Google Scholar] [CrossRef]
- Khaliullin, R.N.; Schieber, J.D. Self-consistent modeling of constraint release in a single-chain mean-field slip-link model to bidisperse systems. Macromolecules 2009, 42, 7504–7517. [Google Scholar] [CrossRef]
- McLeish, T.C.B. Tube theory of entangled polymer dynamics. Adv. Phys. 2002, 61, 1379–1527. [Google Scholar] [CrossRef]
- Graham, R.S.; Likhtman, A.E.; McLeish, T.C.B. Microscopic theory of linear, entangled polymer chains under rapid deformation including chain stretch and convective constraint release. J. Rheol. 2003, 47, 1171–1200. [Google Scholar] [CrossRef]
- Katzarova, M.; Kashyap, T.; Schieber, J.D.; Venerus, D.C. Linear viscoelastic behavior of bidisperse polystyrene blends: Experiments and slip-link predictions. Rheologica Acta 2018, 57, 327–338. [Google Scholar] [CrossRef]
- Marrucci, G. Relaxation by reptation and tube enlargement—A model for polydisperse polymers. J. Polym. Sci. B 1985, 23, 159–177. [Google Scholar] [CrossRef]
- Qiao, X.; Sawada, T.; Matsumiya, Y.; Watanabe, H. Constraint release in moderately entangled monodisperse star polyisoprene systems. Macromolecules 2006, 39, 7333–7341. [Google Scholar] [CrossRef]
- Ramirez-Hernández, A.; Peters, B.L.; Andreev, M.; Schieber, J.D.; de Pablo, J.J. A multichain polymer slip-spring model with fluctuating number of entanglements for linear and nonlinear rheology. J. Chem. Phys. 2015, 143, 243147. [Google Scholar] [CrossRef] [Green Version]
- Ramirez-Hernandez, A.; Peters, B.L.; Schneider, L.; Andreev, M.; Schieber, J.D.; Müller, M.; de Pablo, J.J. A multi-chain polymer slip-spring model with fluctuating number of entanglements: Density fluctuations, confinement, and phase separation. J. Chem. Phys. 2017, 146, 014903. [Google Scholar] [CrossRef] [Green Version]
- Masubuchi, Y. Multichain slip-spring simulations for branch polymers. Macromolecules 2019, 51, 10184–10193. [Google Scholar] [CrossRef]
- Sgouros, A.P.; Megariotis, G.; Theodorou, D.N. Slip-spring model for the linear and nonlinear viscoelastic properties of molten polyethylene derived from atomistic simulations. Macromolecules 2017, 50, 4524–4541. [Google Scholar] [CrossRef]
- Vogiatzis, G.G.; Megariotis, G.; Theodorou, D.N. Equation of state based slip spring model for entangled polymer dynamics. Macromolecules 2017, 50, 3004–3029. [Google Scholar] [CrossRef]
- Nafar Sefiddashti, M.H.; Edwards, M.G.; Khomami, B. Individual chain dynamics of a polyethylene melt undergoing steady shear flow. J. Rheol. 2015, 59, 119–153. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Mavrantzas, V.G.; Theodorou, D.N. Segmental dynamics in polyethylene melts through atomistic molecular dynamics simulations. In Recent Research Topics and Developments in Chemical Physics: From Quantum Scale to Macroscale; Transworld Research Network: Kerala, India, 2008; Volume 661, pp. 179–196. [Google Scholar]
- Loring, R.F. Diffusion of a flexible polymer chain in a disordered medium. J. Chem. Phys. 1988, 88, 6631–6640. [Google Scholar] [CrossRef]
- Dua, A.; Cherayil, B.J. The anomalous diffusion of polymers in random media. J. Chem. Phys. 2000, 112, 421–427. [Google Scholar] [CrossRef]
- Fuchs, M.; Schweizer, K.S. Polymer-mode-coupling theory of finite-size-fluctuation effects in entangled solutions, melts, and gels. 1. General formulation and predictions. Macromolecules 1997, 30, 5133–5155. [Google Scholar] [CrossRef]
- Schweizer, K.S. Microscopic theory of the dynamics of polymeric liquids: General formulation of a mode–mode-coupling approach. J. Chem. Phys. 1989, 91, 5802. [Google Scholar] [CrossRef]
- Schweizer, K.S. Mode-coupling theory of the dynamics of polymer liquids: Qualitative predictions for flexible chain and ring melts. J. Chem. Phys. 1989, 91, 5822–5839. [Google Scholar] [CrossRef]
- Schweizer, K.S.; Szamel, G. Mode-coupling theory ofentangled polymer fluids. Transp. Theory Stat. Phys. 1995, 24, 947–977. [Google Scholar] [CrossRef]
- Karatrantos, A.; Clarke, N. A theoretical model for the prediction of diffusion in polymer/SWCNT nanocomposites. Soft Matter 2011, 7, 7334–7341. [Google Scholar] [CrossRef]
- Meth, J.S.; Gam, S.; Choi, J.; Lin, C.C.; Composto, R.J. Excluded volume model for the reduction fo polymer diffusion into nanocomposites. J. Phys. Chem. B 2013, 117, 15675–15683. [Google Scholar]
- Martin, J.; Krutyeva, M.; Monkenbusch, M.; Arbe, A.; Allgaier, J.; Radulescu, A.; Falus, P.; Maiz, J.; Mijangos, C.; Colmenero, J.; et al. Direct observation of confined single chain dynamics by neutron scattering. Phys. Rev. Lett. 2010, 104, 197801. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.C.; Gam, S.; Meth, J.S.; Clarke, N.; Winey, K.I. Do attractive polymer-nanoparticle interactions retard polymer diffusion in nanocomposites. Macromolecules 2013, 46, 4502–4509. [Google Scholar] [CrossRef]
- Pierleoni, C.; Capone, B.; Hansen, J.P. A soft effective segment representation of semidilute polymer solutions. J. Chem. Phys. 2007, 127, 171102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Locatelli, E.; Capone, B.; Likos, C.N. Multiblob coarse-graining for mixtures of long polymers and soft colloids. J. Chem. Phys. 2016, 145, 174901. [Google Scholar] [CrossRef] [PubMed] [Green Version]

















© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karatrantos, A.; Composto, R.J.; Winey, K.I.; Kröger, M.; Clarke, N. Modeling of Entangled Polymer Diffusion in Melts and Nanocomposites: A Review. Polymers 2019, 11, 876. https://doi.org/10.3390/polym11050876
Karatrantos A, Composto RJ, Winey KI, Kröger M, Clarke N. Modeling of Entangled Polymer Diffusion in Melts and Nanocomposites: A Review. Polymers. 2019; 11(5):876. https://doi.org/10.3390/polym11050876
Chicago/Turabian StyleKaratrantos, Argyrios, Russell J. Composto, Karen I. Winey, Martin Kröger, and Nigel Clarke. 2019. "Modeling of Entangled Polymer Diffusion in Melts and Nanocomposites: A Review" Polymers 11, no. 5: 876. https://doi.org/10.3390/polym11050876
APA StyleKaratrantos, A., Composto, R. J., Winey, K. I., Kröger, M., & Clarke, N. (2019). Modeling of Entangled Polymer Diffusion in Melts and Nanocomposites: A Review. Polymers, 11(5), 876. https://doi.org/10.3390/polym11050876