Analytical Modeling of the Postcracking Response Observed in Hybrid Steel/Polypropylene Fiber-Reinforced Concrete
Abstract
:1. Introduction
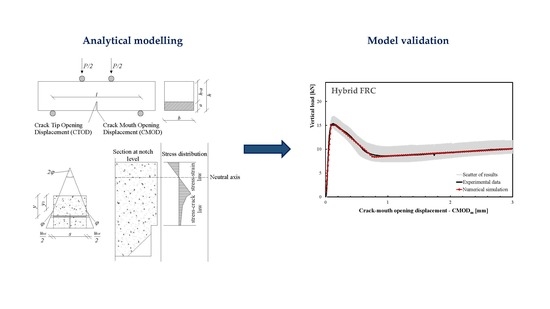
2. Model Formulation
2.1. Constitutive Rules
2.2. Compatibility Equations
2.3. Equilibrium Equations
3. Summary of Experimental Results
- HySP-FRC-75-0, only including S fibers (S = 0.75% of the matrix);
- HySP-FRC-55-20, with 25% of the S fibers replaced by P fibers;
- HySP-FRC-37.5, with 50% of the S fibers replaced by P fibers;
- HySP-FRC-20-55, with 75% of the S fibers replaced by P fibers;
- HySP-FRC-0-75, only including P fibers (P = 0.75 % of the matrix).
- First crack strength (flf):where Plf represents the first crack load (in N), b; h and l are the width (in mm), height (in mm) and spam length (in mm) of the tested beam, respectively; and a0 (in mm) represents the notch depth.
- Work capacity indices: U1 and U2 (energy absorption values) represent the areas under the vertical load (P)–CTOD curve in a representative range for the serviceability limit state (i.e., considering a CTOD ranging between CTOD0 and CTOD0+0.6) and for the ultimate state (i.e., considering a CTOD ranging between CTOD0+0.6 and CTOD0.6+3), respectively.
- Equivalent post-cracking strengths: The first one (feq(0–0.6)) is supposed to be significant for the serviceability limit state (evaluated as a function of the U1 parameter), whereas the second one (feq(0.6–3)) is rather relevant for the ultimate state (evaluated as a function of the U2 parameter).
- Ductility indices: D0 and D1 can be determined with the following equations:
4. Model Validation
5. Conclusions
- The proposed model is based on sufficiently general, yet analytically expressed, normal stress–crack opening relationships, which can potentially simulate the various possible responses observed in experimental tests on FRC specimens.
- The model parameters were identified for each mixture, and a very good agreement was obtained between the experimental results and the simulation output for all the HyFRC specimens considered in this study.
- Moreover, the parameters obtained for the normal stress–crack opening identified for the various HyFRC specimens exhibited a regular variability with respect to the fiber content and proportions of each specimen.
Author Contributions
Funding
Conflicts of Interest
References
- Hajek, P. Concrete structures for sustainability in a changing world. Procedia Eng. 2017, 171, 207–214. [Google Scholar] [CrossRef]
- Etse, G.; Willam, K. Fracture energy formulation for inelastic behavior of plain concrete. J. Eng. Mech. 1994, 120, 1983–2011. [Google Scholar] [CrossRef]
- Soltanzadeh, F.; Barros, J.A.O.; Santos, R.F.C. High performance fiber reinforced concrete for the shear reinforcement: Experimental and numerical research. Constr. Build. Mater. 2015, 77, 94–109. [Google Scholar] [CrossRef] [Green Version]
- Balea, A.; Fuente, E.; Blanco, A.; Negro, C. Nanocelluloses: Natural-Based Materials for Fiber-Reinforced Cement Composites. A Critical Review. Polymers 2019, 11, 518. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, D.; Jiang, Y.; Huang, B.; Du, Y.; Zhao, J.; Zhang, X.; Wang, F.A. ZnS/CaZnOS Heterojunction for Efficient Mechanical-to-Optical Energy Conversion by Conduction Band Offset. Adv. Mater. 2020, 32, 1907747. [Google Scholar] [CrossRef] [PubMed]
- Olawale, D.O.; Sullivan, G.; Dickens, T.; Tsalickis, S.; Okoli, O.I.; Sobanjo, J.O.; Wang, B. Development of a triboluminescence-based sensor system for concrete structures. Struct. Health Monit. 2011, 11, 139–147. [Google Scholar] [CrossRef]
- Yew, M.K.; Yew, M.C.; Beh, J.H.; Saw, L.H.; Lee, F.W.; Ng, T.C. Influence of high-performance polypropylene fibre and heat-treated dura oil palm shell on durability properties of lightweight concrete. Eur. J. Environ. Civ. Eng. 2018, 1–20. [Google Scholar] [CrossRef]
- Yoo, D.Y.; Banthia, N. Experimental and numerical analysis of the flexural response of amorphous metallic fiber reinforced concrete. Mater. Struct. 2017, 50, 64. [Google Scholar] [CrossRef]
- Naaman, A.E.; Reinhardt, H.W. Proposed classification of HPFRC composites based on their tensile response. Mater. Struct. 2006, 39, 547–555. [Google Scholar] [CrossRef]
- Pacheco, F.; Christ, R.; Gil, A.M.; Tutikian, B.F. SEM and 3D microtomography application to investigate the distribution of fibers in advanced cementitious composites. Rev. Ibracon Estrut. Mater. 2016, 9, 824–841. [Google Scholar] [CrossRef] [Green Version]
- Breitenbücher, R.; Meschke, G.; Song, F.; Zhan, Y. Experimental, analytical and numerical analysis of the pullout behaviour of steel fibers considering different fiber types, inclinations and concrete strengths. Struct. Concr. 2014, 15, 126–135. [Google Scholar] [CrossRef]
- Chu, S.H.; Li, L.G.; Kwan, A.K.H. Fibre factors governing the fresh and hardened properties of steel FRC. Constr. Build. Mater. 2018, 186, 1228–1238. [Google Scholar] [CrossRef]
- Reiterman, P.; Jogl, M.; Baumelt, V.; Seifrt, J. Development and Mix Design of HPC and UHPFRC. Adv. Mater. Res. 2014, 982, 130–135. [Google Scholar] [CrossRef]
- ACI Committee 544 544.1R-96. State-of-the-Art Report on Fiber Reinforced Concrete; (Reapproved 2009); American Concrete Institute: Farmington Hills, MI, USA, 2002. [Google Scholar]
- ACI Committee 506 506.1R-98. Committee Report on Fiber Reinforced Shotcrete; American Concrete Institute: Farmington Hills, MI, USA, 1998. [Google Scholar]
- UNI 11037. Steel Fiber to be Used in the Preparation of Reinforced Concrete Conglomerate; UNSIDER-Commissione Tecnica Unsider: Milano, Italy, 2003. [Google Scholar]
- ASTM-A820/A820M-06. Standard Specification for Steel Fibers for Fiber-Reinforced Concrete; ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]
- CNR-DT 204/2006. Guide for the Design and Construction of Fiber-Reinforced Concrete Structures; ROME–CNR; Italian National Research Council: Rome, Italy, 2007. [Google Scholar]
- UNI-11039-1. Steel Fiber Reinforced Concrete—Definitions, Classification and Designation; UNI Editions: Milan, Italy, 2003. [Google Scholar]
- UNI-11039-2. Steel Fiber Reinforced Concrete—Test Method to Determine the First Crack Strength and Ductility Indexes; UNI Editions: Milan, Italy, 2003. [Google Scholar]
- RILEM TC 162-TDF. Test and design methods for steel fiber reinforced concrete. Design of steel fiber reinforced concrete using the σ-w method: Principles and applications. Mater. Struct. 2002, 35, 262–278. [Google Scholar]
- fib Model-Code. Model Code 2010; Comité Euro-International du Beton-Federation International de la Precontrainte: Paris, France, 2013; Volume 1. [Google Scholar]
- fib Model-Code. Model Code 2010; Comité Euro-International du Beton-Federation International de la Precontrainte: Paris, France, 2013; Volume 2. [Google Scholar]
- prEN 14889-1. Fibers for Concrete-Part 1: Steel Fibers-Definition, Specifications and Conformity; BSI: London, UK, 2006. [Google Scholar]
- Wille, K.; Naaman, A.E. Pullout behavior of high-strength steel fibers embedded in ultra-high-performance concrete. ACI Mater. J. 2012, 109, 479–488. [Google Scholar]
- Martinelli, E.; Caggiano, A.; Xargay, H. An experimental study on the post-cracking behaviour of Hybrid Industrial/Recycled Steel Fiber-Reinforced Concrete. Constr. Build. Mater. 2015, 94, 290–298. [Google Scholar] [CrossRef]
- Caggiano, A.; Xargay, H.; Folino, P.; Martinelli, E. Experimental and numerical characterization of the bond behavior of steel fibers recovered from waste tires embedded in cementitious matrices. Cem. Concr. Compos. 2015, 62, 146–155. [Google Scholar] [CrossRef]
- Caggiano, A.; Folino, P.; Lima, C.; Martinelli, E.; Pepe, M. On the mechanical response of hybrid fiber reinforced concrete with recycled and industrial steel fibers. Constr. Build. Mater. 2017, 147, 286–295. [Google Scholar] [CrossRef]
- Gillani, S.A.A.; Toumi, A.; Turatsinze, A. Cyclic bridging law of steel fibre-reinforced and rubberised cement-based materials. Eur. J. Environ. Civ. Eng. 2020. [Google Scholar] [CrossRef]
- de Andrade Silva, F.; Mobasher, B.; Toledo Filho, R.D. Fatigue behavior of sisal fiber reinforced cement composites. Mater. Sci. Eng. A 2010, 527, 5507–5513. [Google Scholar] [CrossRef]
- Ferreira, S.R.; Pepe, M.; Martinelli, E.; de Andrade Silva, F.; Toledo Filho, R.D. Influence of natural fibers characteristics on the interface mechanics with cement based matrices. Compos. Part B 2018, 140, 183–196. [Google Scholar] [CrossRef]
- Caggiano, A.; Cremona, M.; Faella, C.; Lima, C.; Martinelli, E. Fracture behavior of concrete beams reinforced with mixed long/short steel fibers. Constr. Build. Mater. 2012, 37, 832–840. [Google Scholar] [CrossRef]
- Aly, T.; Sanjayan, J.G.; Collins, F. Effect of polypropylene fibers on shrinkage and cracking of concretes. Mater. Struct. 2008, 41, 1741. [Google Scholar] [CrossRef]
- Hsie, M.; Tu, C.; Song, P. Mechanical properties of polypropylene hybrid fiber reinforced concrete. Mater. Sci. Eng. A 2008, 494, 153–157. [Google Scholar] [CrossRef]
- Buratti, N.; Mazzotti, C.; Savoia, M. Post-cracking behaviour of steel and macro-synthetic fibre-reinforced concretes. Constr. Build. Mater. 2011, 25, 2713–2722. [Google Scholar] [CrossRef]
- Caggiano, A.; Gambarelli, S.; Martinelli, E.; Nisticò, N.; Pepe, M. Experimental characterization of the post-cracking response in hybrid steel/polypropylene fiber-reinforced concrete. Constr. Build. Mater. 2016, 125, 1035–1043. [Google Scholar] [CrossRef]
- Kim, D.J.; Park, S.H.; Ryu, G.S.; Koh, K.T. Comparative flexural behavior of hybrid ultra high performance fiber reinforced concrete with different macro fibers. Constr. Build. Mater. 2011, 25, 4144–4155. [Google Scholar] [CrossRef]
- Wickramasinghe, S.; Do, T.; Tran, P. FDM-Based 3D Printing of Polymer and Associated Composite: A Review on Mechanical Properties, Defects and Treatments. Polymers 2020, 12, 1529. [Google Scholar] [CrossRef] [PubMed]
- Oliver, J. Consistent characteristic length for smeared cracking models. Int. J. Numer. Methods Eng. 1989, 28, 461–474. [Google Scholar] [CrossRef]
- Rots, J.; Nauta, P.; Kusters, G.; Blaauwendraad, J. Smeared crack approach and fracture localization in concrete. Heron 1985, 30, 1. [Google Scholar]
- Caggiano, A.; Etse, G.; Martinelli, E. Zero-thickness interface model formulation for failure behavior of fiber-reinforced cementitious composites. Comput. Struct. 2012, 9899, 23–32. [Google Scholar] [CrossRef]
- Carol, I.; Prat, P.; Lopez, C. Normal/shear cracking model: Applications to discrete crack analysis. ASCE J. Eng. Mech. 1997, 123, 765–773. [Google Scholar] [CrossRef]
- Bazant, Z.; Tabbara, M.; Kazemi, M.; Pijaudier-Cabot, G. Random particle model for fracture of aggregate or fiber composites. J. Eng. Mech. 1990, 116, 1686–1705. [Google Scholar] [CrossRef]
- Meschke, G.; Dumstorff, P. Energy-based modeling of cohesive and cohesionless cracks via X-FEM. Comput. Methods Appl. Mech. Eng. 2007, 196, 2338–2357. [Google Scholar] [CrossRef]
- Oliver, J.; Huespe, A.; Pulido, M.; Chaves, E. From continuum mechanics to fracture mechanics: The strong discontinuity approach. Eng. Fract. Mech. 2002, 69, 113–136. [Google Scholar] [CrossRef]
- Singh, I.; Mishra, B.; Pant, M. An enrichment based new criterion for the simulation of multiple interacting cracks using element free Galerkin method. Int. J. Fract. 2011, 167, 157–171. [Google Scholar] [CrossRef]
- Olesen, J.F. Fictitious crack propagation in fiber-reinforced concrete beams. J. Eng. Mech. 2001, 127, 273–280. [Google Scholar] [CrossRef]
- Hillerborg, A. Application of the fictitious crack model to different types of materials. Int. J. Fract. 1991, 51, 95–102. [Google Scholar]
- Zhang, J.; Li, V.C. Simulation of crack propagation in fiber-reinforced concrete by fracture mechanics. Cem. Concr. Res. 2004, 34, 333–339. [Google Scholar] [CrossRef]
- Walter, R.; Olesen, J.F. Cohesive mixed mode fracture modelling and experiments. Eng. Fract. Mech. 2008, 75, 5163–5176. [Google Scholar] [CrossRef]
- Park, K.; Paulino, G.H.; Roesler, J. Cohesive fracture model for functionally graded fiber reinforced concrete. Cem. Concr. Res. 2010, 40, 956–965. [Google Scholar] [CrossRef]
- Oh, B.H.; Kim, J.C.; Choi, Y.C. Fracture behavior of concrete members reinforced with structural synthetic fibers. Eng. Fract. Mech. 2007, 74, 243–257. [Google Scholar] [CrossRef]
- Ulfkjær, J.P.; Krenk, S.; Brincker, R. Analytical model for fictitious crack propagation in concrete beams. J. Eng. Mech. 1995, 121, 7–15. [Google Scholar] [CrossRef] [Green Version]
- WIRAND®® FIBRE FS7. Technical Data Sheet Rev. 10; Date 08.11.2010; Maccaferri: Zola Predosa, Italy, 2010. [Google Scholar]
- FIBROMAC®®. 12-Mono-Filamentary Polypropylene Fibre; TECHNICAL DATA SHEET Rev. 10, Date 08.11.2010; Maccaferri: Zola Predosa, Italy, 2010. [Google Scholar]
- EN 12390–4: 2009. Testing Hardened Concrete-Compressive Strength of Test Specimens; BSI: London, UK, 2009. [Google Scholar]












| bi | ai | w |
|---|---|---|
| 1 | ||
| 0 | 0 |
| Mixtures | ft | α1 | w1 | α2 | w2 | α3 | w3 | w4 | E/s |
|---|---|---|---|---|---|---|---|---|---|
| [MPa] | - | [mm] | - | [mm] | - | [mm] | [mm] | [MPa/mm] | |
| HySP-FRC-75-0 | 2.650 | 1.000 | 0.050 | 0.700 | 0.363 | 1.240 | 3.750 | 5.000 | 52.213 |
| HySP-FRC-55-20 | 2.700 | 1.000 | 0.050 | 0.720 | 0.390 | 1.135 | 3.750 | 5.000 | 52.213 |
| HySP-FRC-37.5 | 2.765 | 1.000 | 0.050 | 0.555 | 0.500 | 0.780 | 3.750 | 5.000 | 52.213 |
| HySP-FRC-20-55 | 2.400 | 0.890 | 0.220 | 0.400 | 0.600 | 0.480 | 3.750 | 5.000 | 104.425 |
| HySP-FRC-0-75 | 2.400 | 0.860 | 0.380 | 0.305 | 0.850 | 0.288 | 3.750 | 5.000 | 104.425 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caggiano, A.; Pepe, M.; Xargay, H.; Martinelli, E. Analytical Modeling of the Postcracking Response Observed in Hybrid Steel/Polypropylene Fiber-Reinforced Concrete. Polymers 2020, 12, 1864. https://doi.org/10.3390/polym12091864
Caggiano A, Pepe M, Xargay H, Martinelli E. Analytical Modeling of the Postcracking Response Observed in Hybrid Steel/Polypropylene Fiber-Reinforced Concrete. Polymers. 2020; 12(9):1864. https://doi.org/10.3390/polym12091864
Chicago/Turabian StyleCaggiano, Antonio, Marco Pepe, Hernan Xargay, and Enzo Martinelli. 2020. "Analytical Modeling of the Postcracking Response Observed in Hybrid Steel/Polypropylene Fiber-Reinforced Concrete" Polymers 12, no. 9: 1864. https://doi.org/10.3390/polym12091864
APA StyleCaggiano, A., Pepe, M., Xargay, H., & Martinelli, E. (2020). Analytical Modeling of the Postcracking Response Observed in Hybrid Steel/Polypropylene Fiber-Reinforced Concrete. Polymers, 12(9), 1864. https://doi.org/10.3390/polym12091864