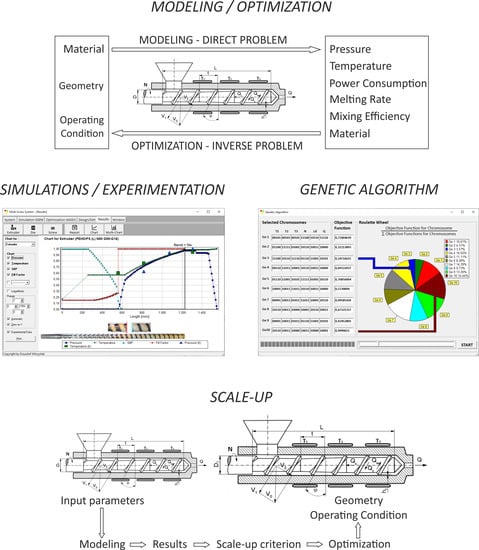
Optimization and Scale-Up for Polymer Extrusion
Abstract
:1. Introduction
2. Modeling of Extrusion
3. Optimization for Extrusion
- -
- the parameters of the optimization problem are processed in coded form and not directly;
- -
- searching for a solution is carried out from a certain population and not from one point, which ensures that the probability of getting stuck in a local extreme is low;
- -
- the selection rules are probabilistic rather than deterministic;
- -
- a new search area of expected higher quality is determined based on the previous experiences, thanks to which, despite some randomness, they do not amount to accidental wandering;
- -
- only the objective function is used and not its derivatives.
- -
- identifying the process variables to be optimized, and defining the range of their variation;
- -
- selecting the optimization criteria, and prescribing their boundaries and quantifying the relative importance by weighting;
- -
- searching the solution, maximizing the objective function.
- -
- encoding input variables which are represented as strings of bits, referred to as chromosomes;
- -
- defining an objective function that evaluates a value of each genotype, i.e., a set of chromosomes;
- -
- generation of a randomly selected initial population;
- -
- definition of genetic operators, i.e., reproduction, crossover and mutation, which search the response space using probabilistic rules.
4. Scale-Up for Extrusion
- -
- can tackle a single scaling criterion only (e.g., shear rate, melting rate, pumping rate) and only a single step of extrusion process (e.g., melting, melt conveying);
- -
- can take into account only a few global geometric or operation parameters (screw diameter D, channel depth H, screw length L, and screw speed N);
- -
- are based on the simplified mathematical description of extrusion process, have limited quantitative predictive capability, and do not cover the overall extrusion process;
- -
- are rigid in terms of the scale-up criteria which means that the user cannot include a new criterion.
- -
- considering simultaneously several process criteria;
- -
- selecting single parameters (e.g., average shear rate) or functions (e.g., shear rate profile along the screw) as scale-up criteria;
- -
- flexibility in selecting/defining the criteria.
- -
- simulation of the extrusion process to obtain the responses data of the reference extruder under a specific set of geometry/operating process parameters (input parameters => modeling => results);
- -
- defining the scaling-up criteria (results => scale-up criteria);
- -
- specifying the fixed and known parameters of the target extruder, e.g., screw diameter D, and length/diameter ratio L/D;
- -
- performing the scaling-up procedure by minimizing the differences between the values of the selected process response parameters of the reference and target extruders, which were defined in the second step (optimization => geometry/operating conditions).
- -
- the ratio of the total flow rate to the drag flow rate, i.e., Q/(WHND), where Q is the flow rate, W is the screw channel with, H is the screw channel height, N is the screw speed, and D is the screw diameter;
- -
- the specific mechanical energy, defined by the energy consumption per unit output;
- -
- the pressure change over the unit channel, i.e., ΔpL/H, where Δp is the pressure change, L is the screw length, and H is the screw channel height;
- -
- the relative melting length, i.e., Lm/L, where Lm is the screw length required for melting and L is the screw length;
- -
- the average shear rate/shear stress;
- -
- the overall viscous dissipation, i.e., Tavg/Tb or Tmaz/Tb, where Tavg is the average melt temperature, Tmaz is the maximum melt temperature, and Tb is the barrel temperature;
- -
- the average residence time;
- -
- the WATS index which is the measure of the mixing degree [147].
5. Future Perspectives
- -
- improvement of the models of extrusion processes which are the basis for optimization/scale-up procedures, and which could be based on the very promising concept of the coupled (DEM/CFD) modeling using the Discrete Element Method (DEM) for modeling of solid conveying and Computational Fluid Dynamics (CFD) for modeling of melting/melt flow [5];
- -
- coupling the models of starve fed extrusion and flood fed extrusion which would allow a smooth transition between them;
- -
- extending the use of optimization/scale-up procedures to more demanding extrusion processes, e.g., extrusion of polymer blends, composites, filled polymers, reactive extrusions, and others;
- -
- improvement of optimization procedures which was recently discussed in the literature [154];
- -
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Underwood, W.M. Experimental Method for Designing Extrusion Screws. Chem. Eng. Prog. 1962, 58, 59. [Google Scholar]
- Verbraak, C.P.J.M.; Meijer, H.E.H. Screw Design in Injection Molding. Polym. Eng. Sci. 1989, 29, 479–487. [Google Scholar] [CrossRef]
- Rauwendaal, C. Polymer Extrusion, 5th ed.; Carl Hanser Verlag: Munich, Germany, 2014; ISBN 978-1-56990-516-6. [Google Scholar]
- Tadmor, Z.; Gogos, C.G. Principles of Polymer Processing, 2nd ed.; John Wiley & Sons Inc.: New York, NY, USA, 2006; ISBN 978-0-471-38770-1. [Google Scholar]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J.; Buziak, K. Fundamentals of Global Modeling for Polymer Extrusion. Polymers 2019, 11, 2106. [Google Scholar] [CrossRef] [Green Version]
- Tadmor, Z.; Klein, I. Engineering Principles of Plasticating Extrusion; Van Nostrand Reinhold Co.: New York, NY, USA, 1970; ISBN 978-0442156350. [Google Scholar]
- Hensen, F.; Knappe, W.; Potente, H. Handbuch der Kunststoff-Extrusiontechnik. Grundlagen; Carl Hanser Verlag: Munich, Germany, 1989; ISBN 978-3446143395. [Google Scholar]
- White, J.L.; Potente, H. Screw Extrusion. Science and Technology; Hanser Publishers: Munich, Germany, 2003; ISBN 978-3-446-19624-7. [Google Scholar]
- Osswald, T.; Hernandez-Ortiz, J.P. Polymer Processing. Modeling and Simulation; Carl Hanser Verlag: Munich, Germany, 2006; ISBN 978-3-446-40381-9. [Google Scholar]
- Agassant, J.F.; Avenas, P.; Carreau, P.J.; Vergnes, B.; Vincent, M. Polymer Processing. Principles and Modelling, 2nd ed.; Carl Hanser Verlag: Munich, Germany, 2017; ISBN 978-1-56990-605-7. [Google Scholar]
- Ariffin, A.; Ahmad, M.S.B. Review: Single Screw Extruder in Particulate Filler Composite. Polym. Plast. Technol. 2011, 50, 395–403. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J. Multipurpose Computer Model for Screw Processing of Plastics. Polym. Plast. Technol. 2012, 51, 626–633. [Google Scholar] [CrossRef]
- Teixeira, C.; Gaspar-Cunha, A.; Covas, J.A. Flow and Heat Transfer Along the Length of a Co-rotating Twin Screw Extruder. Polym. Plast. Technol. 2012, 51, 1567–1577. [Google Scholar] [CrossRef]
- Malik, M.; Kalyon, D.M.; Golba, J.C., Jr. Simulation of Co-Rotating Twin Screw Extrusion Process Subject to Pressure-Dependent Wall Slip at Barrel and Screw Surfaces: 3D FEM Analysis for Combinations of Forward- and Reverse-Conveying Screw Elements. Int. Polym. Proc. 2014, 29, 51–62. [Google Scholar] [CrossRef]
- Hyvärinen, M.; Jabeen, R.; Kärki, T. The Modeling of Extrusion Processes for Polymers—A Review. Polymers 2020, 12, 1306. [Google Scholar] [CrossRef]
- Tadmor, Z.; Klein, I. Computer Programs for Plastic Engineers; Reinhold Book Corporation: New York, NY, USA, 1968. [Google Scholar]
- Klein, I.; Klein, R.J. The SPR System of CAE Software. In Computer Modeling for Extrusion and Other Continuous Polymer Processes; O’Brien, K.T., Ed.; Hanser Publishers: New York, NY, USA, 1992; Chapter 5; pp. 103–252. ISBN 978-1569900680. [Google Scholar]
- Agur, E.E.; Vlachopoulos, J. Numerical Simulation of a Single-Screw Plasticating Extruder. Polym. Eng. Sci. 1982, 22, 1084–1094. [Google Scholar] [CrossRef]
- Potente, H.; Hanhart, W.; Schöppner, V. Potential Applications for Computer-aided Extruder Design. Int. Polym. Proc. 1993, 8, 335–344. [Google Scholar] [CrossRef]
- Potente, H.; Hanhart, W.; Reski, T. Design and Processing Optimization of Extruder Screws. Polym. Eng. Sci. 1994, 34, 937–945. [Google Scholar] [CrossRef]
- Sebastian, D.H.; Rakos, R. Extrusion Process Analysis with PASS. In Computer Modeling for Extrusion and Other Continuous Polymer Processes; O’Brien, K.T., Ed.; Hanser Publishers: New York, NY, USA, 1992; Chapter 7; pp. 331–448. ISBN 978-1569900680. [Google Scholar]
- Wilczyński, K. A Computer Model for Single-Screw Plasticating Extrusion. Polym. Plast. Technol. 1996, 35, 449–477. [Google Scholar] [CrossRef]
- Wilczyński, K. Single Screw Extrusion Model for Plasticating Extruders. Polym. Plast. Technol. 1999, 38, 581–608. [Google Scholar] [CrossRef]
- Fukase, H.; Kunio, T.; Shinya, S.; Nomura, A. A Plasticating Model for Single-Screw Extruders. Polym. Eng. Sci. 1982, 22, 578–586. [Google Scholar] [CrossRef]
- Zawadsky, E.; Karnis, J. Mathematical Model of a Single-Screw Plasticating Extruder. J. Rheol. Acta 1985, 24, 556–565. [Google Scholar] [CrossRef]
- Vincelette, A.R.; Guerrero, C.S.; Carreau, P.J.; Lafleur, P.G. A Model for Single-Screw Plasticating Extruders. Int. Polym. Proc. 1989, 4, 232–241. [Google Scholar] [CrossRef]
- Amellal, K.; Lafleur, P.G. Computer Simulation of Conventional and Barrier Screw Extruders. Plast. Rub. Compos. 1993, 19, 227–239. [Google Scholar]
- Gaspar-Cunha, A.; Covas, J.A. The Plasticating Sequence in Barrier Extrusion Screws Part I: Modeling. Polym. Eng. Sci. 2014, 54, 1791–1803. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Covas, J.A. The Plasticating Sequence in Barrier Extrusion Screws Part II: Experimental Assessment. Polym. Plast. Technol. 2014, 53, 1456–1466. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J.; Buziak, K. Experimental Study for Extrusion of Polypropylene/Wood Flour Composites. Int. Polym. Proc. 2015, 30, 113–120. [Google Scholar] [CrossRef]
- Wilczyński, K.; Buziak, K.; Wilczyński, K.J.; Lewandowski, A.; Nastaj, A. Computer Modeling for Single-Screw Extrusion of Wood-Plastic Composites. Polymers 2018, 10, 295. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; White, J.L. Dimensionless Non-Newtonian Isothermal Simulation and Scale-up Considerations for Modular Intermeshing Corotating Twin Screw Extruders. Int. Polym. Proc. 1991, 6, 304–310. [Google Scholar] [CrossRef]
- White, J.L.; Chen, Z. Simulation of Non-Isothermal Flow in Modular Co-Rotating Twin Screw Extrusion. Polym. Eng. Sci. 1994, 34, 229–237. [Google Scholar] [CrossRef]
- Bawiskar, S.; White, J.L. Solids Conveying and Melting in a Starve Fed Self-wiping Co-Rotating Twin Screw Extruder. Int. Polym. Proc. 1995, 10, 105–110. [Google Scholar] [CrossRef]
- Bawiskar, S.; White, J.L. Melting Model for Modular Self Wiping Co-Rotating Twin Screw Extruders. Polym. Eng. Sci. 1998, 38, 727–740. [Google Scholar] [CrossRef]
- Bawiskar, S.; White, J.L. A Composite Model for Solid Conveying, Melting, Pressure and Fill Factor Profiles in Modular Co-Rotating Twin Screw Extruders. Int. Polym. Proc. 1997, 12, 331–340. [Google Scholar] [CrossRef]
- White, J.L.; Kim, B.-J.; Bawiskar, S.; Keum, J.M. Development of a Global Computer Software for Modular Self-Wiping Corotating Twin Screw Extruders. Polym. Plast. Technol. 2001, 40, 385–405. [Google Scholar] [CrossRef]
- White, J.L.; Keum, J.; Jung, H.; Ban, K.; Bumm, S. Corotating Twin-Screw Extrusion Reactive Extrusion-Devolatilization Model and Software. Polym. Plast. Technol. 2006, 45, 539–548. [Google Scholar] [CrossRef]
- Potente, H.; Melisch, U.; Palluch, K.P. A Physico-Mathematical Model for Solids Conveying in Co-Rotating Twin Screw Extruders. Int. Polym. Proc. 1996, 11, 29–41. [Google Scholar] [CrossRef]
- Potente, H.; Melisch, U. Theoretical and Experimental Investigations of the Melting of Pellets in Co-Rotating Twin-Screw Extruders. Int. Polym. Proc. 1996, 11, 101–108. [Google Scholar] [CrossRef]
- Potente, H.; Ansalh, J.; Wittemeier, R. Throughput Characteristics of Tightly Intermeshing Co-rotating Twin Screw Extruders. Int. Polym. Proc. 1990, 5, 208–216. [Google Scholar] [CrossRef]
- Potente, H.; Ansalh, J.; Klarholz, B. Design of Tightly Intermeshing Co-Rotating Twin Screw Extruders. Int. Polym. Proc. 1994, 9, 11–25. [Google Scholar] [CrossRef]
- Potente, H.; Bastian, M.; Flecke, J. Design of a Compounding Extruder by Means of the SIGMA Simulation Software. Adv. Polym. Technol. 1999, 18, 147–170. [Google Scholar] [CrossRef]
- Vergnes, B.; Delacour, M.L.; Souveton, G.; Bouvier, J.M. A Study of Polymer Melting in a Co-Rotating Twin Screw Extruder. In Proceedings of the International Polymer Processing Society 15th Annual Meeting (PPS-15), Hertogenbosch, The Netherlands, 31 May–4 June 1999. [Google Scholar]
- Vergnes, B.; Souveton, G.; Delacour, M.L.; Ainser, A. Experimental and Theoretical Study of Polymer Melting in a Co-rotating Twin Screw Extruder. Int. Polym. Proc. 2001, 16, 351–362. [Google Scholar] [CrossRef]
- Tayeb, J.; Vergnes, B.; Della Valle, G. A Basic Model for a Twin-Screw Extruder. J. Food Sci. 1989, 54, 1047–1056. [Google Scholar] [CrossRef]
- Vergnes, B.; Valle, G.D.; Delamare, L. A Global Computer Software for Polymer Flows in Corotating Twin Screw Extruders. Polym. Eng. Sci. 1998, 38, 1781–1792. [Google Scholar] [CrossRef]
- Canedo, E.L. Computer Simulation of Plastics Compounding Operations in Twin-Screw Extruders. SPE ANTEC Technol. Pap. 1999, 45, 310–316. [Google Scholar]
- Hong, M.-H.; White, J.L. Fluid Mechanics of Intermeshing Counter-Rotating Twin Screw Extruders. Int. Polym. Proc. 1998, 13, 342–346. [Google Scholar] [CrossRef]
- Hong, M.H.; White, J.L. Simulation of Flow in an Intermeshing Modular Counter-Rotating Twin Screw Extruder: Non-Newtonian and Non-Isothermal Behavior. Int. Polym. Proc. 1999, 14, 136–143. [Google Scholar] [CrossRef]
- Wilczyński, K.; White, J.L. Experimental Study of Melting in an Intermeshing Counter-Rotating Twin Screw Extruder. Int. Polym. Proc. 2001, 16, 257–262. [Google Scholar] [CrossRef]
- Wilczyński, K.; White, J.L. Melting Model for Intermeshing Counter-Rotating Twin-Screw Extruders. Polym. Eng. Sci. 2003, 43, 1715–1726. [Google Scholar] [CrossRef]
- Wilczyński, K.; Jiang, Q.; White, J.L. A Composite Model for Melting, Pressure and Fill Factor Profiles in a Metered Fed Closely Intermeshing Counter-Rotating Twin Screw Extruder. Int. Polym. Proc. 2007, 22, 198–203. [Google Scholar] [CrossRef]
- Jiang, Q.; White, J.L.; Yang, J. A Global Model for Closely Intermeshing Counter-Rotating Twin Screw Extruders with Flood Feeding. Int. Polym. Proc. 2010, 25, 223–235. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J. Modeling of the Polymer Melt Flow in a Twin Screw Counter-Rotating Extrusion Process. Part II. Simulation and Experimental Studies—Verification of the Adopted Model. Polimery 2011, 56, 45–50. [Google Scholar] [CrossRef]
- Wilczyński, K.; Lewandowski, A.; Wilczyński, K.J. Experimental Study of Melting of LDPE/PS Polyblend in an Intermeshing Counter-Rotating Twin Screw Extruder. Polym. Eng. Sci. 2012, 52, 449–458. [Google Scholar] [CrossRef]
- Lewandowski, A.; Wilczyński, K.J.; Nastaj, A.; Wilczyński, K. A Composite Model for an Intermeshing Counter-Rotating Twin-Screw Extruder and its Experimental Verification. Polym. Eng. Sci. 2015, 55, 2838–2848. [Google Scholar] [CrossRef]
- Wilczyński, K.; Lewandowski, A.; Wilczyński, K.J. Experimental Study for Starve-Fed Single Screw Extrusion of Thermoplastics. Polym. Eng. Sci. 2012, 52, 1258–1270. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Wilczyński, K.J. Melting Model for Starve Fed Single Screw Extrusion of Thermoplastics. Int. Polym. Proc. 2013, 28, 34–42. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Nastaj, A.; Lewandowski, A.; Wilczyński, K. A Composite Model for Starve Fed Single Screw Extrusion of Thermoplastics. Polym. Eng. Sci. 2014, 54, 2362–2374. [Google Scholar] [CrossRef]
- Wilczynski, K.J. Experimental and Theoretical Study on Screw Filling in Starve Fed Single Screw Extruders. Int. Polym. Proc. 2018, 33, 171–179. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Lewandowski, A.; Nastaj, A.; Wilczyński, K. Modeling for Starve Fed/Flood Fed Mixing Single-Screw Extruders. Int. Polym. Proc. 2016, 31, 82–91. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Lewandowski, A.; Nastaj, A.; Wilczyński, K. A Global Model for Starve-Fed Nonconventional Single-Screw Extrusion of Thermoplastics. Adv. Polym. Technol. 2017, 36, 23–35. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Lewandowski, A.; Wilczyński, K. Experimental Study of Melting of Polymer Blends in a Starve Fed Single Screw Extruder. Polym. Eng. Sci. 2016, 56, 1349–1356. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Nastaj, A.; Wilczyński, K. A Computer Model for Starve-Fed Single-Screw Extrusion of Polymer Blends. Adv. Polym. Technol. 2018, 37, 2142–2151. [Google Scholar] [CrossRef]
- Wilczyński, K.; Buziak, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J. Modeling for Single Screw Extrusion of Wood Plastic Composites. In Proceedings of the Polymer Processing Society Conference (PPS2015), Graz, Austria, 21–25 September 2015; p. 170. [Google Scholar]
- Wilczyński, K.J.; Buziak, K. A Computer Model for Starve Fed Single Screw Extrusion of Wood Plastic Composites. Polymers 2021, 13, 1252. [Google Scholar] [CrossRef]
- Nastaj, A.; Wilczyński, K. Optimization for Starve Fed/Flood Fed Single Screw Extrusion of Polymeric Materials. Polymers 2020, 12, 149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wilczyński, K. Rheology in Polymer Processing. Modeling and Simulation; Carl Hanser Verlag: Munich, Germany, 2021; ISBN 978-1-56990-660-6. [Google Scholar]
- Lopez-Latorre, L.; McKelvey, J.M. Melting and Pressurization in Starve Feed Extrusion. Adv. Polym. Technol. 1984, 3, 355–364. [Google Scholar] [CrossRef]
- Isherwood, D.P.; Pieris, R.N.; Kassatly, J. The Effect of Metered Starve Feeding on the Performance of a Small Extruder. J. Eng. Ind. 1984, 106, 132–136. [Google Scholar] [CrossRef]
- Strand, S.R.; Spalding, M.A.; Hyun, S.K. Modeling of the Solids-Conveying Section of a Starve Fed Single Screw Plasticating Extruder. SPE ANTEC Technol. Pap. 1992, 38, 2537–2541. [Google Scholar]
- Gale, M. Compounding with Single-Screw Extruders. Adv. Polym. Technol. 1997, 16, 251–262. [Google Scholar] [CrossRef]
- Thompson, M.R.; Donoian, G.; Christiano, J.P. Melting Mechanism of a Starved-Fed Single-Screw Extruder for Calcium Carbonate Filled Polyethylene. Polym. Eng. Sci. 2000, 40, 2014–2026. [Google Scholar] [CrossRef]
- Rathner, R.; Tranchida, D.; Roland, W.; Ruemer, F.; Buchmann, K.; Amsüss, P.; Steinbichler, G. Properties of Starve-fed extrusion on a material containing a VHMWPE. Polymers 2021, 13, 944. [Google Scholar] [CrossRef] [PubMed]
- Maddock, B.H.; Smith, D.J. Extruder Design by Computer Printout. SPE J. 1972, 28, 12–17. [Google Scholar]
- Helmy, H.A.A.; Parnaby, J. Computer—Aided Optimal Melt Screw Design. Polym. Eng. Sci. 1976, 16, 437–449. [Google Scholar] [CrossRef]
- Potente, H.; Hanhart, W.; Klarholz, B.; Schöppner, V. Extruderschnecken durch Simulation optimieren. Kunststoffe 1992, 82, 939–944. [Google Scholar]
- Potente, H.; Krell, B. Screw optimization by means of DOE and multiple regression. In Proceedings of the 55th Annual Technical Conferences of the Society of Plastics Engineers (ANTEC 1997), Toronto, ON, Canada, 27 April–2 May 1997; pp. 135–139. [Google Scholar]
- Potente, H.; Schöppner, V.; Ujma, A. Successful Simulation of Wall—Slipping Plastics. J. Polym. Eng. 1997, 17, 153–170. [Google Scholar] [CrossRef]
- Thibodeau, C.A.; Lafleur, P.G. Computer Design and Screw Optimization. In Proceedings of the 58th Annual Technical Conference of the Society of Plastics Engineers (ANTEC 2000), Orlando, FL, USA, 7–11 May 2000; pp. 276–282. [Google Scholar]
- Thibodeau, C.A.; Lafleur, P.G. Computer Design and Screw Optimization. In Proceedings of the Polymer Processing Society 16th Annual Meeting (PPS-16), Shanghai, China, 18–23 June 2000; p. 15. [Google Scholar]
- Wilczyński, K.; Nastaj, A.; Krutysz, P. Optymalizacja Procesu Wytłaczania Jednoślimakowego Tworzyw Sztucznych. Metoda Statystyczna. Mechanik 2003, 10, 618. [Google Scholar]
- Wilczyński, K. SSEM: A Computer Model for a Polymer Single—Screw Extrusion. J. Mater. Process. Technol. 2001, 3, 308–313. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Longman Publishing Co.: Boston, MA, USA, 1989; ISBN 978-0-201-15767-3. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A. Modeling and Optimization of Single Screw Extrusion. Ph.D. Thesis, University of Minho, Guimarães, Portugal, 2000. [Google Scholar]
- Covas, J.A.; Cunha, A.G.; Oliveira, P. An Optimization Approach to Practical Problems in Plasticating Single Screw Extrusion. Polym. Eng. Sci. 1999, 39, 443–456. [Google Scholar] [CrossRef]
- Covas, J.A.; Gaspar-Cunha, A. The Use of an Optimization Approach to the Design of Extrusion Screw. In Proceedings of the Polymer Processing Society 16th Annual Meeting (PPS-16), Shanghai, China, 18–23 June 2000. [Google Scholar]
- Gaspar-Cunha, A.; Covas, J.A. The Design of Extrusion Screw: An Optimization Approach. Int. Polym. Proc. 2001, 16, 229–240. [Google Scholar] [CrossRef] [Green Version]
- Gaspar-Cunha, A.; Covas, J.A.; Vergnes, B. An Optimization Methodology for Setting the Operating Conditions in Twin-Screw Extrusion. In Proceedings of the Polymer Processing Society 18th Annual Meeting (PPS-18), Guimaraes, Portugal, 18–21 June 2002. [Google Scholar]
- Gaspar-Cunha, A.; Poulesquen, A.; Vergnes, B.; Covas, J.A. Optimization of Processing Conditions for Polymer Twin-Screw Extrusion. Int. Polym. Proc. 2002, 17, 201–213. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Covas, J.; Vergnes, B. Defining the Configuration of Co-Rotating Twin-Screw Extruders with Multiobjective Evolutionary Algorithms. Polym. Eng. Sci. 2005, 45, 1159–1173. [Google Scholar] [CrossRef]
- Teixeira, C.; Covas, J.A.; Berzin, F.; Vergnes, B.; Gaspar-Cunha, A. Application of Evolutionary Algorithms to the Definition of the Optimal Twin-Screw Extruder Configuration for Starch Cationization. Polym. Eng. Sci. 2011, 51, 330–340. [Google Scholar] [CrossRef]
- Covas, J.A.; Gaspar-Cunha, A. Polymer Extrusion—Setting the Operating Conditions and Defining the Screw Geometry. In Optimization in Polymer Processing; Gaspar-Cunha, A., Covas, J.A., Eds.; Nova Science Publishers Inc.: Hauppauge, NY, USA, 2011; Chapter 5; pp. 1–35. ISBN 978-1-61122-818-2. [Google Scholar]
- Nastaj, A.; Wilczyński, K. Optimization for Single Screw Extrusion of Polymeric Materials—Experimental Studies. Polimery 2018, 1, 38–44. [Google Scholar] [CrossRef]
- Nastaj, A.; Wilczyński, K. Process Optimization for Single Screw Extrusion of Polymeric Materials—Simulation Studies. Polimery 2018, 4, 297–304. [Google Scholar] [CrossRef]
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Gaspar-Cunha, A. Modeling and Optimization of the Injection-Molding Process: A Review. Adv. Polym. Technol. 2016, 37, 429–449. [Google Scholar] [CrossRef]
- Mok, S.L.; Kwong, C.K.; Lau, W.S. A Hybrid Neural Network and Genetic Algorithm Approach to the Determination of Initial Process Parameters for Injection Moulding. Int. J. Adv. Manuf. Technol. 2001, 18, 404–409. [Google Scholar] [CrossRef]
- Turng, L.-S.; Peić, M. Computer Aided Process and Design Optimization for Injection Moulding. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2002, 216, 1523–1532. [Google Scholar] [CrossRef]
- Zhou, J.; Turng, L.-S.; Kramschuster, A. Single and Multi Objective Optimization for Injection Molding Using Numerical Simulation with Surrogate Models and Genetic Algorithms. Intern. Polym. Process. 2006, 21, 509–520. [Google Scholar] [CrossRef]
- Kurtaran, H.; Ozcelik, B.; Erzurumlu, T. Warpage Optimization of a Bus Ceiling Lamp Base Using Neural Network Model and Genetic Algorithm. J. Mater. Process. Technol. 2005, 169, 314–319. [Google Scholar] [CrossRef]
- Ozcelik, B.; Erzurumlu, T. Determination of Effecting Dimensional Parameters on Warpage of Thin Shell Plastic Parts Using Integrated Response Surface Method and Genetic Algorithm. Int. Commun. Heat Mass 2005, 32, 1085–1094. [Google Scholar] [CrossRef]
- Ozcelik, B.; Erzurumlu, T. Comparison of the Warpage Optimization in the Plastic Injection Molding Using ANOVA, Neural Network Model and Genetic Algorithm. J. Mater. Process. Technol. 2006, 171, 437–445. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Viana, J.C. Using Multi-Objective Evolutionary Algorithms to Optimize Mechanical Properties of Injection Molded Parts. Int. Polym. Proc. 2005, 20, 274–285. [Google Scholar] [CrossRef]
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Gaspar-Cunha, A. Using Multiobjective Evolutionary Algorithms in the Optimization of Operating Conditions of Polymer Injection Molding. Polym. Eng. Sci. 2010, 50, 1667–1678. [Google Scholar] [CrossRef]
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Gaspar-Cunha, A. Using Multi-Objective Evolutionary Algorithms for Optimization of the Cooling System in Polymer Injection Molding. Int. Polym. Proc. 2012, 27, 213–223. [Google Scholar] [CrossRef] [Green Version]
- Shen, C.; Wang, L.; Li, Q. Optimization of Injection Molding Process Parameters Using Combination of Artificial Neural Network and Genetic Algorithm Method. J. Mater. Process. Technol. 2007, 183, 412–418. [Google Scholar] [CrossRef]
- Chen, W.-C.; Fu, G.-L.; Tai, P.-H.; Deng, W.-J. Process Parameter Optimization for MIMO Plastic Injection Molding via Soft Computing. Expert Syst. Appl. 2009, 36, 1114–1122. [Google Scholar] [CrossRef]
- Chen, W.C.; Lin, Y.F.; Liou, P.H. A Multi-Objective Quality Optimization System for Injection Molding Process Parameters. Adv. Mat. Res. 2014, 945–949, 478–483. [Google Scholar] [CrossRef]
- Wu, C.-Y.; Ku, C.-C.; Pai, H.-Y. Injection Molding Optimization with Weld Line Design Constraint Using Distributed Multi-Population Genetic Algorithm. Int. J. Adv. Manuf. Technol. 2011, 52, 131–141. [Google Scholar] [CrossRef]
- Ding, L.P.; Tan, J.R.; Wei, Z.; Chen, W.L.; Gao, Z. Multi-Objective Performance Design of Injection Molding Machine via a New Multi-Objective Optimization Algorithm. Int. J. Innov. Comput. Inform. Control 2011, 7, 3939–3949. [Google Scholar]
- Natalini, M.; Sasso, M.; Amodio, D. Comparison of Numerical and Experimental Data in Multi-Objective Optimization of a Thermoplastic Molded Part. Int. Polym. Proc. 2013, 28, 84–106. [Google Scholar] [CrossRef]
- Tsai, K.-M.; Luo, H.-J. Comparison of Injection Molding Process Windows for Plastic Lens Established by Artificial Neural Network and Response Surface Methodology. Int. J. Adv. Manuf. Technol. 2015, 77, 1599–1611. [Google Scholar] [CrossRef]
- Alam, K.; Kamal, M.R. Runner Balancing by a Direct Genetic Optimization of Shrinkage. Polym. Eng. Sci. 2004, 44, 1949–1959. [Google Scholar] [CrossRef]
- Alam, K.; Kamal, M.R. A Robust Optimization of Injection Molding Runner Balancing. Comput. Chem. Eng. 2005, 29, 1934–1944. [Google Scholar] [CrossRef]
- Young, W.-B. Gate Location Optimization in Liquid Composite Molding Using Genetic Algorithms. J. Compos. Mater. 1994, 28, 1098–1113. [Google Scholar] [CrossRef]
- Kim, B.Y.; Nam, G.J.; Ryu, H.S.; Lee, J.W. Optimization of Filling Process in RTM Using Genetic Algorithm. Korea Aust. Rheol. J. 2000, 12, 83–92. [Google Scholar]
- Lam, Y.C.; Zhai, L.Y.; Tai, K.; Fok, S.C. An Evolutionary Approach for Cooling System Optimization in Plastic Injection Moulding. Int. J. Prod. Res. 2004, 42, 2047–2061. [Google Scholar] [CrossRef]
- Qiao, H. A Systematic Computer-Aided Approach to Cooling System Optimal Design in Plastic Injection Molding. Int. J. Mech. Sci. 2006, 48, 430–439. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, Z.; Tan, J. Multiobjective Optimization of Injection Molding Parameters Based on Soft Computing and Variable Complexity Method. Int. J. Adv. Manuf. Technol. 2013, 66, 907–916. [Google Scholar] [CrossRef]
- Kashyap, S.; Datta, D. Process parameter optimization of plastic injection molding: A review. Int. J. Plast. Technol. 2015, 19, 1–18. [Google Scholar] [CrossRef]
- Wilczyński, K.; Narowski, P. Strategy for Problem Solving of Filling Imbalance in Geometrically Balanced Injection Molds. Polymers 2020, 12, 805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McKelvey, J.M. Polymer Processing; John Wiley & Sons Inc.: New York, NY, USA, 1962; ISBN 978-0471584438. [Google Scholar]
- Stevens, M.J.; Covas, J.A. Extruder Principles and Operation; Springer: Berlin/Heidelberg, Germany, 1995; ISBN 978-94-010-4247-5. [Google Scholar] [CrossRef]
- Campbell, G.A.; Spalding, M.A. Analyzing and Troubleshooting Single-Screw Extruders; Carl Hanser Verlag: Munich, Germany, 2013; ISBN 978-3-446-41371-9. [Google Scholar]
- Chung, C.I. Extrusion of Polymers. Theory and Practice, 3rd ed.; Carl Hanser Verlag: Munich, Germany, 2019; ISBN 978-1-569-907375. [Google Scholar]
- Chen, B.; Zhu, L.; Zhang, F.; Qiu, Y. Process Development and Scale-Up. In Developing Solid Oral Dosage Forms; Elsevier: Amsterdam, The Netherlands, 2017; pp. 821–868. [Google Scholar] [CrossRef]
- Carley, J.F.; McKelvey, J.M. Extruder Scale-Up Theory and Experiments. Ind. Eng. Chem. 1953, 45, 989–992. [Google Scholar] [CrossRef]
- Maddock, B.H. A Visual Analysis of Flow and Mixing in Extruder Screws. Soc. Plast. Eng. J. 1959, 15, 383–389. [Google Scholar]
- Maddock, B.H. Extruder Scale-up by Computer. Polym. Eng. Sci. 1974, 14, 853–858. [Google Scholar] [CrossRef]
- Fenner, R.T.; Williams, J.G. Some Melt Flow and Mechanical Design Aspects of Large Extruders. Polym. Eng. Sci. 1971, 11, 474–483. [Google Scholar] [CrossRef]
- Yi, B.; Fenner, R.T. Scaling-up Plasticating Screw Extruders on the Basis of Similar Melting Performances. Plast. Rubber Process. 1976, 1, 119–123. [Google Scholar]
- Pearson, J.R.A. Scale-up of Single Screw Extruders for Polymer Processing. Plast. Rubber Process. 1976, 1, 113–118. [Google Scholar]
- Potente, H.; Fischer, P. Model Laws for the Design of Single Screw Plasticating Extruders. Kunststoffe 1977, 67, 242–247. [Google Scholar]
- Schenkel, G. Extruder Series with Variable L/D Ratios. Kunststoffe 1978, 68, 155–162. [Google Scholar]
- Chung, C.I. On the Scale-up of Plasticating Extruder Screws. Polym. Eng. Sci. 1984, 24, 626–632. [Google Scholar] [CrossRef]
- Rauwendaal, C. Scale-up of Single Screw Extruders. Polym. Eng. Sci. 1987, 27, 1059–1068. [Google Scholar] [CrossRef]
- Potente, H. Existing Scale-Up Rules for Single-Screw Plasticating Extruders. Int. Polym. Proc. 1991, 6, 267–278. [Google Scholar] [CrossRef]
- Elemans, P.H.M.; Meijer, H.E.H. Scale-up of the Mixing Process in Continuos Mixers. In Mixing and Compounding of Polymers; Manas-Zloczower, I., Tadmor, Z., Eds.; Carl Hanser Verlag: Munich, Germany, 1994; pp. 457–470. ISBN 13: 978-156990-156-4. [Google Scholar]
- Wang, W.; Manas-Zloczower, I. Temporal Distributions: The Basis for the Development of Mixing Indexes for Scale-up of Polymer Processing Equipment. Polym. Eng. Sci. 2001, 41, 1068–1077. [Google Scholar] [CrossRef]
- Menges, G.; Feistkorn, W. Scale-Up of Twin Screw Extruders. Application and Verification with the Example of PVC. Adv. Polym. Technol. 1984, 4, 123–129. [Google Scholar] [CrossRef]
- Ganzeveld, K.J.; Janssen, L.P.B.M. Scale-Up of Counter-Rotating Closely Intermeshing Twin Screw Extruders without and with Reactions. Polym. Eng. Sci. 1990, 30, 1529–1536. [Google Scholar] [CrossRef]
- Nakatani, M. Scale-Up Theory for Twin-Screw Extruder, Keeping the Resin Temperature Unchanged. Adv. Polym. Technol. 1998, 17, 19–22. [Google Scholar] [CrossRef]
- Dryer, B.; Fukuda, G.; Webb, J.; Montemayor, K.; Bigio, D.I.; Andersen, P.; Wetzel, M. Comparison of Scale-up Methods for Dispersive Mixing in Twin-Screw Extruders. Polym. Eng. Sci. 2017, 57, 345–354. [Google Scholar] [CrossRef]
- Potente, H. Scale-up of Mixing Equipments. In Mixing and Compounding of Polymers, 2nd ed.; Manas-Zloczower, I., Ed.; Carl Hanser Verlag: Munich, Germany, 2009; pp. 577–643. ISBN 978-1-56990-660-6. [Google Scholar]
- Covas, J.A.; Gaspar-Cunha, A. Extrusion Scale-up: An Optimization-based Methodology. Int. Polym. Proc. 2009, 24, 67–82. [Google Scholar] [CrossRef]
- Pinto, G.; Tadmor, Z. Mixing and Residence Time Distribution in Melt Screw Extruders. Polym. Eng. Sci. 1970, 10, 279–288. [Google Scholar] [CrossRef]
- Berzin, F.; David, C.; Vergnes, B. Optimization and Scale-Up of Twin-Screw Reactive Extrusion: The Case of EVA Transesterification. Int. Polym. Proc. 2020, 35, 422–428. [Google Scholar] [CrossRef]
- Markarian, J. Compounders Look to Simulation Software for Savings in Time and Costs. Plast. Add. Compd. 2005, 7, 34–37. [Google Scholar] [CrossRef]
- Ortiz-Rodriguez, E.; Tzoganakis, C. Scaling-Up a Reactive Extrusion Operation: A One-Dimensional Simulation Analysis. Int. Polym. Proc. 2010, 25, 242–250. [Google Scholar] [CrossRef]
- Pradel, J.L.; David, C.; Quinebeche, S.; Blondel, P. Scale up Tools in Reactive Extrusion and Compounding Processes. Could 1D-Computer Modeling Be Helpful. AIP Conf. Proc. 2014, 1593, 530–533. [Google Scholar] [CrossRef]
- Covas, J.A.; Gaspar-Cunha, A. A Scaling-up Methodology for Co-rotating Twin-Extruders. In Proceedings of the 27th Annual Meeting of the Polymer Processing Society (PPS-27), Marrakesh, Morocco, 10–14 May 2011; pp. 1–6. [Google Scholar]
- Gaspar-Cunha, A.; Covas, J.A. An Engineering Scale-Up Approach Using Multi-Objective Optimization. Intern. J. Nat. Comp. Res. 2014, 4, 17–30. [Google Scholar] [CrossRef] [Green Version]
- Denysiuk, R.; Recio, G.; Covas, J.A.; Gaspar-Cunha, A. Using Multiobjective Optimization Algorithms and Decision Making Support to Solve Polymer Extrusion Problems. Polym. Eng. Sci. 2018, 58, 493–502. [Google Scholar] [CrossRef]
- Levine, L.; Levine, S. Scale-up, Experimentation, and Data Evaluation. In Extrusion Cooking; Ganjyal, G.M., Ed.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 331–389. [Google Scholar] [CrossRef]
- Haser, A.; Haight, B.; Berghaus, A.; Machado, A.; Martin, C.; Zhang, F. Scale-Up and In-Line Monitoring During Continuous Melt Extrusion of an Amorphous Solid Dispersion. AAPS PharmSciTech 2018, 19, 2818–2827. [Google Scholar] [CrossRef] [PubMed]
- Dhaval, M.; Sharma, S.; Dudhat, K.; Chavda, J. Twin-Screw Extruder in Pharmaceutical Industry: History, Working Principle, Applications, and Marketed Products: An In-depth Review. J. Pharm. Innov. 2020. [Google Scholar] [CrossRef]
- La Galla, A.; Fiorio, R.; Erkoç, M.; Cardon, L.; D’hooge, D.R. Theoretical Evaluation of the Melting Efficiency for the Single-Screw Micro-Extrusion Process: The Case of 3D Printing of ABS. Processes 2020, 8, 1522. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nastaj, A.; Wilczyński, K. Optimization and Scale-Up for Polymer Extrusion. Polymers 2021, 13, 1547. https://doi.org/10.3390/polym13101547
Nastaj A, Wilczyński K. Optimization and Scale-Up for Polymer Extrusion. Polymers. 2021; 13(10):1547. https://doi.org/10.3390/polym13101547
Chicago/Turabian StyleNastaj, Andrzej, and Krzysztof Wilczyński. 2021. "Optimization and Scale-Up for Polymer Extrusion" Polymers 13, no. 10: 1547. https://doi.org/10.3390/polym13101547
APA StyleNastaj, A., & Wilczyński, K. (2021). Optimization and Scale-Up for Polymer Extrusion. Polymers, 13(10), 1547. https://doi.org/10.3390/polym13101547